MCM备赛笔记——图论模型
Key Concept
图论是数学的一个分支,专注于研究图的性质和图之间的关系。在图论中,图是由顶点(或节点)以及连接这些顶点的边(或弧)组成的。图论的模型广泛应用于计算机科学、通信网络、社会网络、生物信息学、城市交通规划等多个领域。
图论的基本模型
-
无向图:
- 顶点之间的边没有方向。无向图常用于表示双向关系,如社交网络中的友谊关系。
-
有向图:
- 顶点之间的边有方向。有向图适用于表达方向性的关系,如网页间的链接。
-
加权图:
- 边或顶点被赋予权重(或成本、容量等)。加权图常用于道路网络,其中权重可以表示距离、时间、费用等。
-
多重图:
- 两个顶点之间可以有多条边。多重图适用于存在多种关系的场景,如航线图。
-
子图:
- 原图的一部分,包含原图的部分顶点和边。
-
完全图:
- 每对顶点之间都恰好有一条边。完全图用于当每个节点都与其他节点直接相连的情况。
-
树:
- 无环连通图。树常用于表示层次结构,如家族树或组织结构。
-
二分图:
- 顶点可分为两个互不相交的集合,图中的每条边连接的两个顶点分别属于这两个不同的集合。二分图适用于匹配问题,如工作分配或婚姻匹配。
使用python的networkx库函数来绘制图
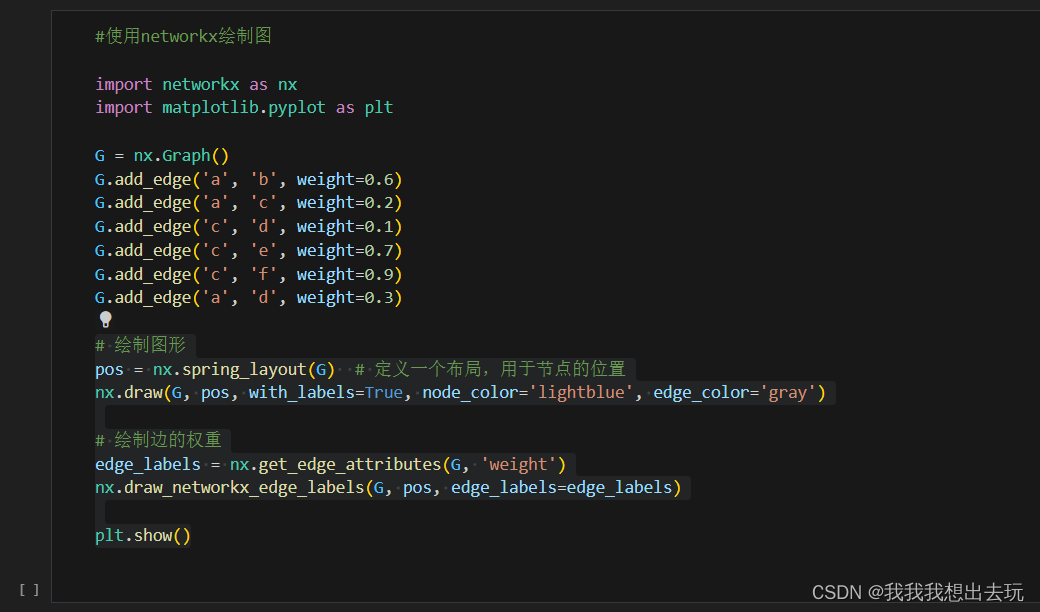

图论问题
-
最短路径问题:
- 在加权图中找到两点间的最短路径,如Dijkstra算法或Bellman-Ford算法。

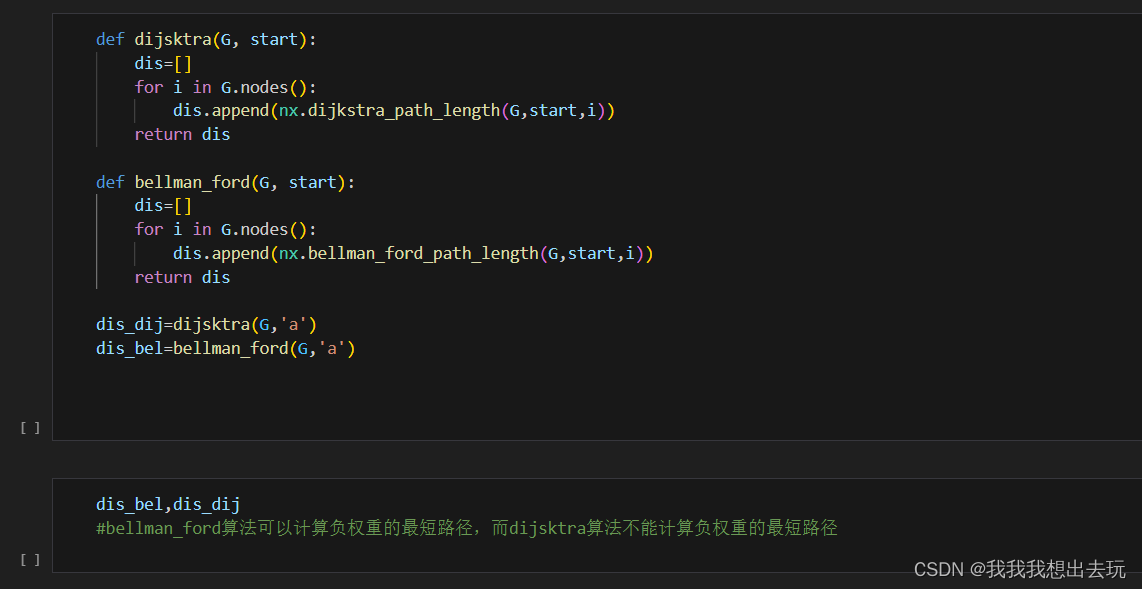
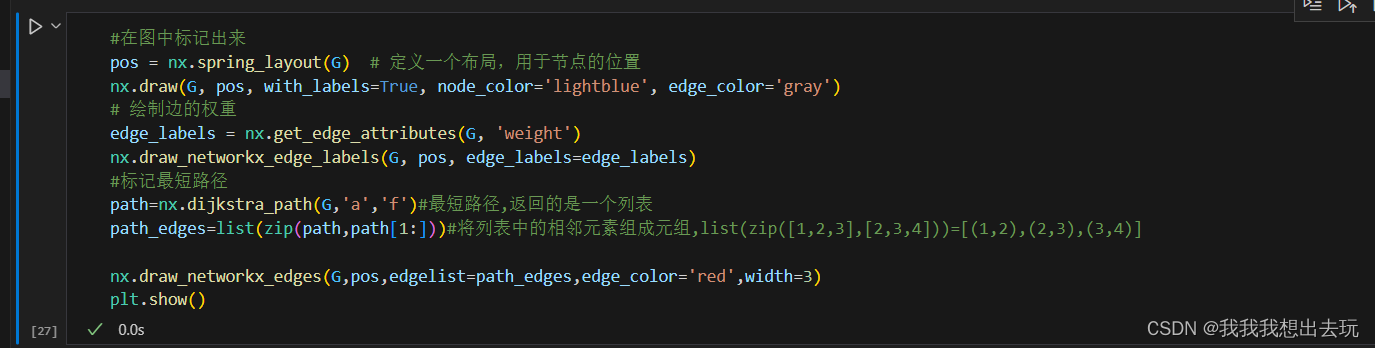

- 在加权图中找到两点间的最短路径,如Dijkstra算法或Bellman-Ford算法。
-
最小生成树
最小生成树这里有两种算法krual算法和prime算法
krual算法更适合稀疏图配合并查集来实现
prime算法更适合稠密图,直接对边进行遍历
#prim算法,更加适合稠密图
#1.任选一个顶点作为起始点,然后找到与其相连的最小权重的边,将这条边加入最小生成树中
#2.然后找到与这两个顶点相连的最小权重的边,将这条边加入最小生成树中
#3.重复上一步,直到所有的顶点都在最小生成树中
#4.最后得到的就是最小生成树def prim(G):mst = []nodes = list(G.nodes())visited = set([nodes[0]]) # 使用集合来快速检查是否访问过while len(visited) != len(nodes):min_edge = Nonemin_weight = float('inf') # 设置一个很大的初始值for u in visited:for v in G.neighbors(u):if v not in visited and G[u][v]['weight'] < min_weight:min_weight = G[u][v]['weight']min_edge = [u, v, {'weight':G[u][v]['weight']}]if min_edge is not None:mst.append(min_edge)visited.add(min_edge[1]) # 添加新顶点到访问过的集合中return mst# 假设G是已经创建好的图
mst = prim(G)
mst#krual算法,更加适合稀疏图
#1.将所有的边按照权重从小到大排序
#2.从权重最小的边开始,如果这条边的两个顶点不在同一个连通分量中,则将这条边加入最小生成树中,否则不加入
#3.重复上一步,直到所有的顶点都在同一个连通分量中
#4.最后得到的就是最小生成树#这里使用并查集来实现查找连通分量
class UnionFind:def __init__(self, nodes):self.parent = {node: node for node in nodes}#初始化每个节点的父节点都是自己def find(self, node):if self.parent[node] != node:self.parent[node] = self.find(self.parent[node])return self.parent[node]def union(self, node1, node2):root1 = self.find(node1)root2 = self.find(node2)if root1 != root2:self.parent[root2] = root1def kruskal(G):mst = []edges = list(G.edges(data=True))edges.sort(key=lambda x: x[2]['weight'])uf = UnionFind(G.nodes())for edge in edges:u, v = edge[0], edge[1]if uf.find(u) != uf.find(v): # 如果u和v不在同一个集合中uf.union(u, v) # 合并集合mst.append(edge) # 加入最小生成树if len(mst) == len(G.nodes()) - 1:breakif len(mst) != len(G.nodes()) - 1:print('该图不是连通图')return mstmst=kruskal(G)
mst
-
网络流问题:
-
最大流问题
#网络最大流问题 #最大流问题是指在一个网络中,从源点到汇点的最大流量是多少 #1.将所有的边的流量初始化为0 #2.在残余网络中找到一条增广路径,如果没有增广路径,则结束 #3.在增广路径上找到最小的残余容量,将这个容量增加到这条路径上 #4.重复上一步,直到没有增广路径 #5.最后得到的就是最大流 import networkx as nx import matplotlib.pyplot as pltG = nx.DiGraph() G.add_edge('s', 'a', capacity=3.0) G.add_edge('s', 'b', capacity=1.0) G.add_edge('a', 'c', capacity=3.0) G.add_edge('b', 'c', capacity=5.0) G.add_edge('b', 'd', capacity=4.0) G.add_edge('d', 'e', capacity=2.0) G.add_edge('c', 't', capacity=2.0) G.add_edge('e', 't', capacity=3.0)# 绘制图形 pos = nx.spring_layout(G) # 定义一个布局,用于节点的位置 nx.draw(G, pos, with_labels=True, node_color='lightblue', edge_color='gray')# 绘制边的权重 edge_labels = nx.get_edge_attributes(G, 'capacity') nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)plt.show()这里直接调用networkx来解决问题
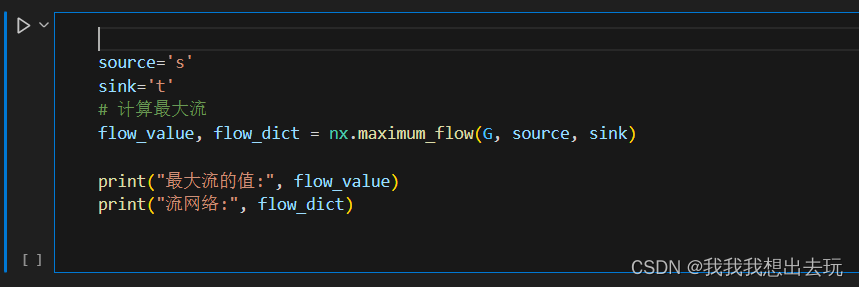
-
-
最大流最小费用问题

#最小费用最大流问题 #最小费用最大流问题是指在一个网络中,从源点到汇点的最大流量是多少,且最小费用是多少 #1.将所有的边的流量初始化为0 #2.在残余网络中找到一条增广路径,如果没有增广路径,则结束 #3.在增广路径上找到最小的残余容量,将这个容量增加到这条路径上 #4.重复上一步,直到没有增广路径 #5.最后得到的就是最大流 #6.计算最小费用 #7.重复上述步骤,直到最小费用不再减少import networkx as nx import matplotlib.pyplot as plt import numpy as npL = [('vs','v2',5,3),('vs','v3',3,6),('v2','v4',2,8),('v3','v2',1,2),('v3','v5',4,2),('v4','v3',1,1),('v4','v5',3,4),('v4','vt',2,10),('v5','vt',5,2)] G = nx.DiGraph() for i in range(len(L)):G.add_edge(L[i][0], L[i][1], capacity=L[i][2], weight=L[i][3]) flow_dict = nx.max_flow_min_cost(G, 'vs', 'vt') min_cost = nx.cost_of_flow(G, flow_dict)node = list(G.nodes()) n = len(node) A = np.zeros((n,n), dtype=int) for i, adj in flow_dict.items():for j, f in adj.items():A[node.index(i), node.index(j)] = fprint("最小费用最大流为:\n", flow_dict) print("最小费用为:\n", min_cost) print("最大流的流量为:\n", sum(A[:, -1])) print("最小费用最大流的邻接矩阵\n", A)
Key Concept Explanation 图论的模型和问题对于理解和解决现实世界中的复杂关系和网络结构具有重要意义。通过将实际问题抽象为图论问题,我们可以应用数学理论和算法来找到有效的解决方案。图论的应用范围非常广泛,从互联网的数据传输到社交网络的分析,再到交通网络的优化,都可以见到图论模型的影子。
相关文章:

MCM备赛笔记——图论模型
Key Concept 图论是数学的一个分支,专注于研究图的性质和图之间的关系。在图论中,图是由顶点(或节点)以及连接这些顶点的边(或弧)组成的。图论的模型广泛应用于计算机科学、通信网络、社会网络、生物信息学…...

算法笔记(动态规划入门题)
1.找零钱 int coinChange(int* coins, int coinsSize, int amount) {int dp[amount 1];memset(dp,-1,sizeof(dp));dp[0] 0;for (int i 1; i < amount; i)for (int j 0; j < coinsSize; j)if (coins[j] < i && dp[i - coins[j]] ! -1)if (dp[i] -1 || dp[…...

开发实践_阶段三
编写一个告知APP。 需求: 1.登录、注册 2.发布定向讯息:检测是否登录,是则向用户或用户组发布 ”名称 时间“ ;否则提示登录 3.讯息接收:检测是否登录,是则查看收到信息(未读数)…...

codegeex和通义灵码辅助编程——以及通义灵码无法登陆的bug解决
通义的速度更快,延迟低,150ms。 codegeex速度慢些,延迟较高,500ms。 个人评价:延迟低的会很好地改善使用体验,所以通义加分。 但是整体功能上还是codegeex强一些,可以选中代码进行对话…...

Android14之DefaultKeyedVector实现(一百八十二)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...
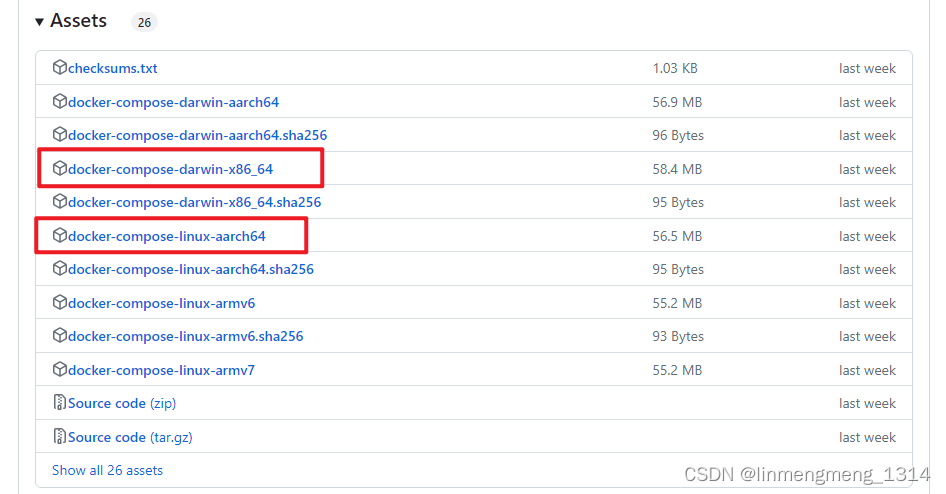
银河麒麟操作系统 v10 中离线安装 Docker
银河麒麟操作系统 v10 中离线安装 Docker 1. 查看系统版本2. 查看 Linux 内核版本(3.10以上)3. 查看 iptabls 版本(1.4以上)4. 判断处理器架构5. 离线下载 Docker 安装包6. 移动解压出来的二进制文件到 /usr/bin 目录中7. 配置 Do…...

如何系统的学习Python
学习 Python 的时候,可以按照以下步骤进行系统学习: 学习 Python 基础知识:首先了解 Python 的基础语法、数据类型、变量和运算符等基本概念。可以通过阅读《Python编程从入门到实践》等经典教材来建立基础。也可以通过翻阅Python官方文档来进…...

Java并发基础:一文讲清util.concurrent包的作用
java.util.concurrent包是 Java 中用于并发编程的重要工具集,提供了线程池、原子变量、并发集合、同步工具类、阻塞队列等一系列高级并发工具类,使用这些工具类可以极大地简化并发编程的难度,减少出错的可能性,提高程序的效率和可…...

C++PythonC# 三语言OpenCV从零开发(2):教程选择
文章目录 相关专栏前言视频教学和官方文档视频教程OpenCV 官方教程最终选择我的最终选择 相关专栏 C&Python&Csharp in OpenCV 前言 OpenCV 有官方的教程和简单的视频教程: OpenCV 官方教程 B站也有相关的视频教学 OpenCV4 C 快速入门视频30讲 - 系列合集 …...

【嘉立创EDA-PCB设计指南】3.网络表概念解读+板框绘制
前言:本文对网络表概念解读板框绘制(确定PCB板子轮廓) 网络表概念解读 在本专栏的上一篇文章【嘉立创EDA-PCB设计指南】2,将设计的原理图转为了PCB,在PCB界面下出现了所有的封装,以及所有的飞线属性&…...
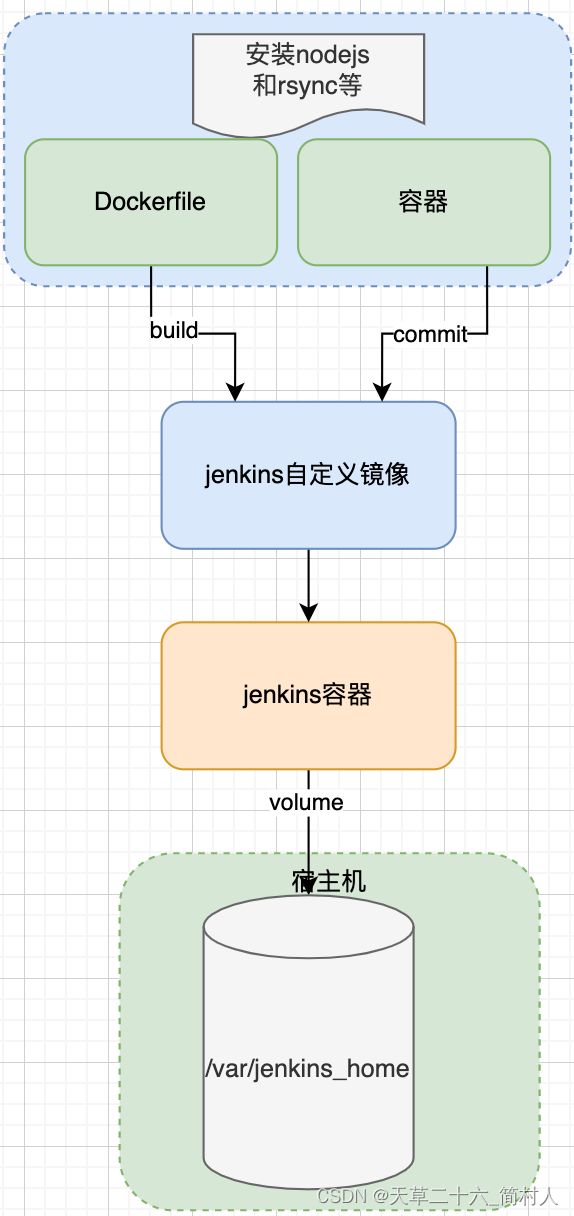
nodejs前端项目的CI/CD实现(二)jenkins的容器化部署
一、背景 docker安装jenkins,可能你会反问,这太简单了,有什么好讲的。 我最近就接手了一个打包项目,它是一个nodejs的前端项目,jenkins已在容器里部署且运行OK。 但是,前端组很追求新技术,不…...

python爬虫案例分享
当然,我可以分享一个基本的Python爬虫示例。这个示例将使用Python的requests库来抓取网页内容,然后使用BeautifulSoup库来解析和提取信息。我们将构建一个简单的爬虫来从一个示例网站抓取标题。 Python爬虫示例 目标 提取某网站的标题。 需要的库 r…...

【CC++】为什么 scanf 函数在读取字符串时不需要用取地址运算符
在C语言中如何使用 scanf 读取字符串 在C语言中,字符串实际上是字符数组,所以我们可以使用scanf函数来读取字符串。但是,需要注意的是,scanf在读取字符串时会在遇到空格、制表符或换行符时停止。因此,它不能用于读取包…...
)
Linux dirs命令教程:dirs命令详解与实例(附实例详解和注意事项)
Linux dirs命令介绍 dirs这是一个内置在shell中的命令,用于显示当前被记忆的目录列表。默认状态下,它会按照stack的方式储存目录,即最后加入的目录会被首先列出来。 Linux dirs命令适用的Linux版本 dirs命令在所有常见的Linux发行版中都适…...
掌握虚拟化:PVE平台安装教程与技术解析
🌟🌌 欢迎来到知识与创意的殿堂 — 远见阁小民的世界!🚀 🌟🧭 在这里,我们一起探索技术的奥秘,一起在知识的海洋中遨游。 🌟🧭 在这里,每个错误都…...

Godot FileDialog无法访问其它盘符的文件
问题描述 使用Godot的FileDialog对象访问Windows系统的文件,例如: func _on_hud_sig_save():var dlg FileDialog.new()dlg.set_access(FileDialog.ACCESS_FILESYSTEM)dlg.set_file_mode(FileDialog.FILE_MODE_SAVE_FILE)add_child(dlg)dlg.popup_cent…...

TestNG注释
目录 TestNG注释列表 BeforeXXX和AfterXXX注释放在超类上时如何工作? 使用BeforeXXX和AfterXXX TestNG注释 TestNG是一个测试框架,旨在简化广泛的测试需求,从单元测试(隔离测试一个类)到集成测试(测试由…...

数据预处理 matlab 数据质量评估
知乎 数据类型转换等 Mathworks 数据预处理 概念辨析 配对是同一批样本的前后比较,独立是两批不同样本的的比较 独立样本是指我们得到的样本是相互独立的。配对样本就是一个样本中的数据与另一个样本中的数据相对应的两个样本。配对样本可以消除由于样本指定的不公…...
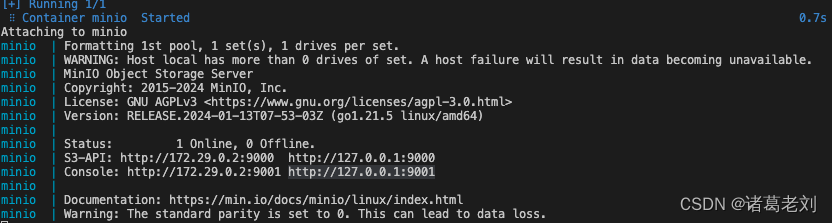
对象存储, 开源MinIO docker-compose.yml 文件
文章目录 python SDK 文档地址:docker-compose.yml 文件控制台使用:应用服务中使用样例: python SDK 文档地址: https://min.io/docs/minio/linux/developers/python/API.html docker-compose.yml 文件 version: 3services:min…...
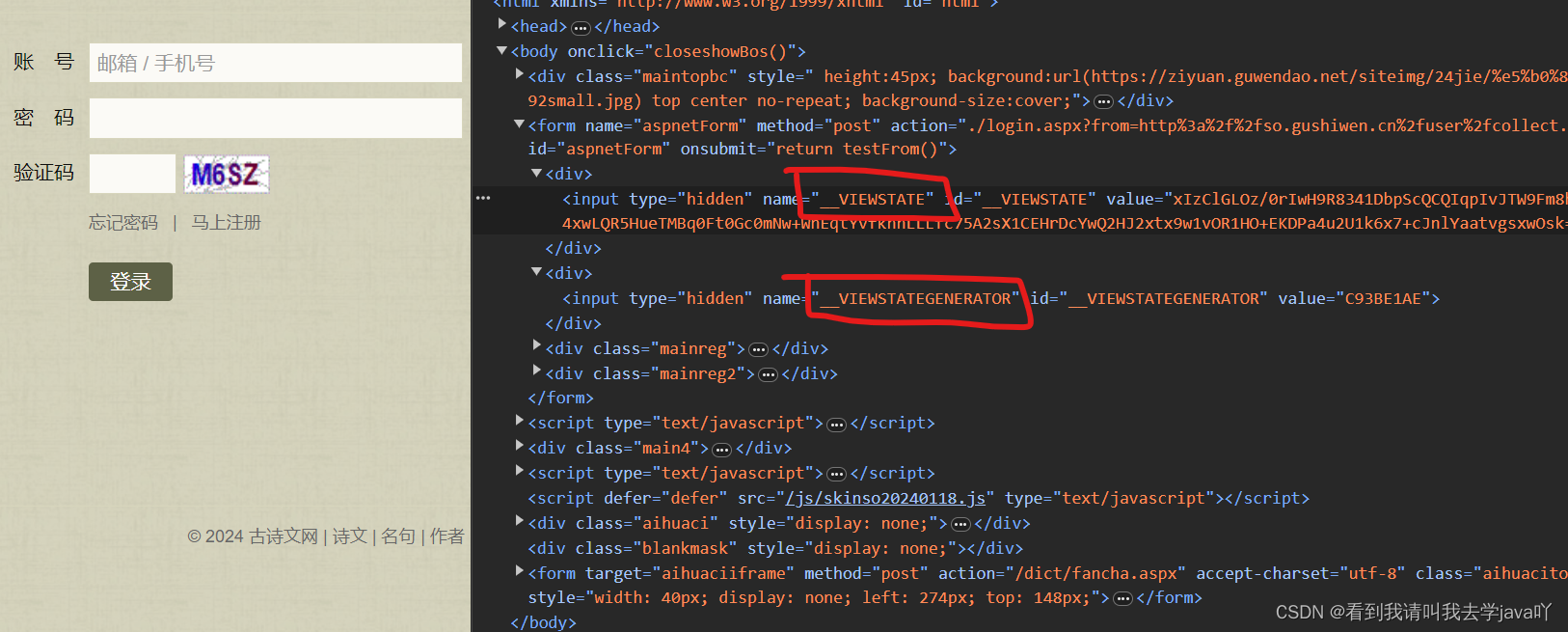
爬虫笔记(一):实战登录古诗文网站
需求:登录古诗文网站,账号+密码+图形验证码 第一:自己注册一个账号+密码哈 第二:图形验证码,需要一个打码平台(充钱,超能力power!)或…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
