高数不定积分72题解答
题目来源:这72道积分题目会积了,绝对是高高手
作者: 湖心亭看雪
第一题
原式=∫15x+3dx=15∫15x+3d(5x+3)=15ln(5x+3)+C\begin{aligned} \text{原式}&=\int \frac{1}{5x+3}dx \\ &=\frac{1}{5} \int\frac{1}{5x+3}d(5x+3) \\ &=\frac{1}{5} ln(5x+3) +C \end{aligned} 原式=∫5x+31dx=51∫5x+31d(5x+3)=51ln(5x+3)+C
第二题
原式=∫e2x+3dx=12∫e2x+3d(2x+3)=12e2x+3+C\begin{aligned} \text{原式}&=\int e^{2x+3}dx \\ &=\frac{1}{2} \int e^{2x+3}d(2x+3) \\ &=\frac{1}{2} e^{2x+3}+C \end{aligned} 原式=∫e2x+3dx=21∫e2x+3d(2x+3)=21e2x+3+C
第三题
原式=∫xex2dx=12∫ex2dx2=12ex2+C\begin{aligned} \text{原式}&=\int xe^{x^2} dx \\ &= \frac{1}{2} \int e^{x^2} dx^2 \\ &=\frac{1}{2}e^{x^2}+C \end{aligned} 原式=∫xex2dx=21∫ex2dx2=21ex2+C
第四题
原式=∫x1−x2dx=−12∫1−x2d(1−x2)=−13(1−x2)32+C\begin{aligned} \text{原式}&=\int x\sqrt{1-x^2} dx \\ &=-\frac{1}{2} \int \sqrt{1-x^2}d(1-x^2) \\ &=-\frac{1}{3}(1-x^2)^{\frac{3}{2} } +C \end{aligned} 原式=∫x1−x2dx=−21∫1−x2d(1−x2)=−31(1−x2)23+C
第五题
原式=∫1x2sin1xdx=−∫sin1xd(1x)=cos(1x)+C\begin{aligned} \text{原式}&=\int \frac{1}{x^2}sin{\frac{1}{x}} dx \\ &=-\int sin{\frac{1}{x}}d(\frac{1}{x} ) \\ &=cos(\frac{1}{x})+C \end{aligned} 原式=∫x21sinx1dx=−∫sinx1d(x1)=cos(x1)+C
第六题
原式=∫e3xxdx=2∫e3x2xdx=23∫e3xd(3x)=23e3x+C\begin{aligned} \text{原式}&=\int \frac{e^{3\sqrt[]{x} }}{\sqrt[]{x}} dx \\ &=2\int \frac{e^{3\sqrt[]{x} }}{2\sqrt{x} } dx \\ &=\frac{2}{3} \int e^{3\sqrt[]{x} }d(3\sqrt[]{x}) \\ &=\frac{2}{3}e^{3\sqrt[]{x}}+C \end{aligned} 原式=∫xe3xdx=2∫2xe3xdx=32∫e3xd(3x)=32e3x+C
第七题
原式=∫1x(1+x6)dx=∫(1x−x51+x6)dx=lnx−16∫11+x6d(1+x6)=lnx−16ln(1+x6)+C\begin{aligned} \text{原式}&=\int \frac{1}{x(1+x^6)} dx \\ &=\int (\frac{1}{x}-\frac{x^5}{1+x^6} )dx \\ &=lnx-\frac{1}{6} \int \frac{1}{1+x^6} d(1+x^6) \\ &=lnx-\frac{1}{6}ln(1+x^6)+C \end{aligned} 原式=∫x(1+x6)1dx=∫(x1−1+x6x5)dx=lnx−61∫1+x61d(1+x6)=lnx−61ln(1+x6)+C
第八题
原式=∫cos2xdx=12∫cos2xd2x=12sin2x+C\begin{aligned} \text{原式}&=\int cos2x dx \\ &=\frac{1}{2} \int cos2x d2x \\ &=\frac{1}{2}sin2x +C \end{aligned} 原式=∫cos2xdx=21∫cos2xd2x=21sin2x+C
第九题
原式=∫sinx5+cosxdx=−∫15+cosxd(5+cosx)=−2∫125+cosxd(5+cosx)=−25+cosx+C\begin{aligned} \text{原式}&=\int \frac{sinx}{\sqrt[]{5+cosx} }dx \\ &=-\int \frac{1}{\sqrt[]{5+cosx}} d(5+cosx) \\ &=-2\int \frac{1}{2~\sqrt[]{5+cosx}}d(5+cosx) \\ &=-2~\sqrt[]{5+cosx}+C \end{aligned} 原式=∫5+cosxsinxdx=−∫5+cosx1d(5+cosx)=−2∫2 5+cosx1d(5+cosx)=−2 5+cosx+C
第十题
原式=∫tan4xdx=∫(sec2x−1)2dx=∫(sec4x−2sec2x+1)dx=∫sec2x(sec2x−2)dx+∫1dx=∫sec2x(tan2x−1)dx+x=∫sec2xtan2xdx−∫sec2dx+x=∫tan2xdtanx−tanx+x=13tan3x−tanx+x+C\begin{aligned} \text{原式}&=\int tan^4xdx \\ &=\int(sec^2x-1)^2dx \\ &=\int (sec^4x-2sec^2x+1)dx \\ &=\int sec^2x(sec^2x-2) dx+\int 1dx \\ &=\int sec^2x(tan^2x-1) dx+x \\ &=\int sec^2xtan^2xdx-\int sec^2 dx+x \\ &=\int tan^2x dtanx -tanx+x \\ &=\frac{1}{3}tan^3x -tanx +x+C \end{aligned} 原式=∫tan4xdx=∫(sec2x−1)2dx=∫(sec4x−2sec2x+1)dx=∫sec2x(sec2x−2)dx+∫1dx=∫sec2x(tan2x−1)dx+x=∫sec2xtan2xdx−∫sec2dx+x=∫tan2xdtanx−tanx+x=31tan3x−tanx+x+C
第十一题
原式=∫e2x1+exdx=∫e2x−1+11+exdx=∫(ex−1)(ex+1)+11+exdx=∫(ex−1)dx+∫11+exdx=ex−x+∫1+ex−ex1+exdx=ex−x+∫1dx−∫ex1+exdx=ex−∫11+exdex=ex−ln(1+ex)+C\begin{aligned} \text{原式}&=\int \frac{e^{2x}}{1+e^x} dx \\ &=\int\frac{e^{2x}-1+1}{1+e^x} dx \\ &=\int\frac{(e^x-1)(e^x+1)+1}{1+e^x} dx \\ &=\int (e^x-1)dx+\int \frac{1}{1+e^x} dx \\ &=e^x-x+\int \frac{1+e^x-e^x}{1+e^x} dx \\ &=e^x-x+\int 1 dx-\int \frac{e^x}{1+e^x} dx \\ &=e^x-\int \frac{1}{1+e^x} de^x \\ &=e^x-ln(1+e^x)+C \end{aligned} 原式=∫1+exe2xdx=∫1+exe2x−1+1dx=∫1+ex(ex−1)(ex+1)+1dx=∫(ex−1)dx+∫1+ex1dx=ex−x+∫1+ex1+ex−exdx=ex−x+∫1dx−∫1+exexdx=ex−∫1+ex1dex=ex−ln(1+ex)+C
第十二题
原式=∫11+exdx=∫1+ex−ex1+exdx=∫1dx−∫ex1+exdx=x−∫11+exdex=x−ln(1+ex)+C\begin{aligned} \text{原式}&=\int \frac{1}{1+e^x} dx \\ &=\int \frac{1+e^x-e^x}{1+e^x} dx \\ &=\int 1 dx-\int \frac{e^x}{1+e^x} dx \\ &=x-\int \frac{1}{1+e^x} de^x \\ &=x-ln(1+e^x)+C \end{aligned} 原式=∫1+ex1dx=∫1+ex1+ex−exdx=∫1dx−∫1+exexdx=x−∫1+ex1dex=x−ln(1+ex)+C
第十三题
原式=∫1xln2x=∫1ln2xdlnx=−1lnx+C\begin{aligned} \text{原式}&=\int \frac{1}{xln^2x} \\ &= \int \frac{1}{ln^2x}dlnx \\ &= -\frac{1}{lnx} + C \end{aligned} 原式=∫xln2x1=∫ln2x1dlnx=−lnx1+C
第十四题
原式=∫1x(1+2lnx)dx=12∫11+2lnxd(2lnx)=12ln(1+2lnx)+C\begin{aligned} \text{原式}&=\int \frac{1}{x(1+2lnx)}dx \\ &=\frac{1}{2} \int \frac{1}{1+2lnx} d(2lnx) \\ &=\frac{1}{2}ln(1+2lnx)+C \end{aligned} 原式=∫x(1+2lnx)1dx=21∫1+2lnx1d(2lnx)=21ln(1+2lnx)+C
第十五题
原式=∫1a2cos2x+b2sin2xdx=∫1cos2xa2+b2tan2xdx=∫sec2xa2+b2tan2xdx=∫1a2+b2tan2xdtanx=1ab∫11+b2tan2xa2d(btanxa)=1abarctan(btanxa)+C\begin{aligned} \text{原式}&=\int \frac{1}{a^2cos^2x+b^2sin^2x}dx \\ &=\int \frac{\frac{1}{cos^2x} }{a^2+b^2tan^2x}dx \\ &=\int \frac{sec^2x }{a^2+b^2tan^2x}dx \\ &=\int \frac{1}{a^2+b^2tan^2x}dtanx \\ &=\frac{1}{ab} \int \frac{1}{1+\frac{b^2tan^2x}{a^2} }d(\frac{btanx}{a}) \\ &=\frac{1}{ab}arctan(\frac{btanx}{a}) +C \end{aligned} 原式=∫a2cos2x+b2sin2x1dx=∫a2+b2tan2xcos2x1dx=∫a2+b2tan2xsec2xdx=∫a2+b2tan2x1dtanx=ab1∫1+a2b2tan2x1d(abtanx)=ab1arctan(abtanx)+C
相关文章:

高数不定积分72题解答
题目来源:这72道积分题目会积了,绝对是高高手 作者: 湖心亭看雪 第一题 原式∫15x3dx15∫15x3d(5x3)15ln(5x3)C\begin{aligned} \text{原式}&\int \frac{1}{5x3}dx \\ &\frac{1}{5} \int\frac{1}{5x3}d(5x3) \\ &\frac{1}{5} ln…...
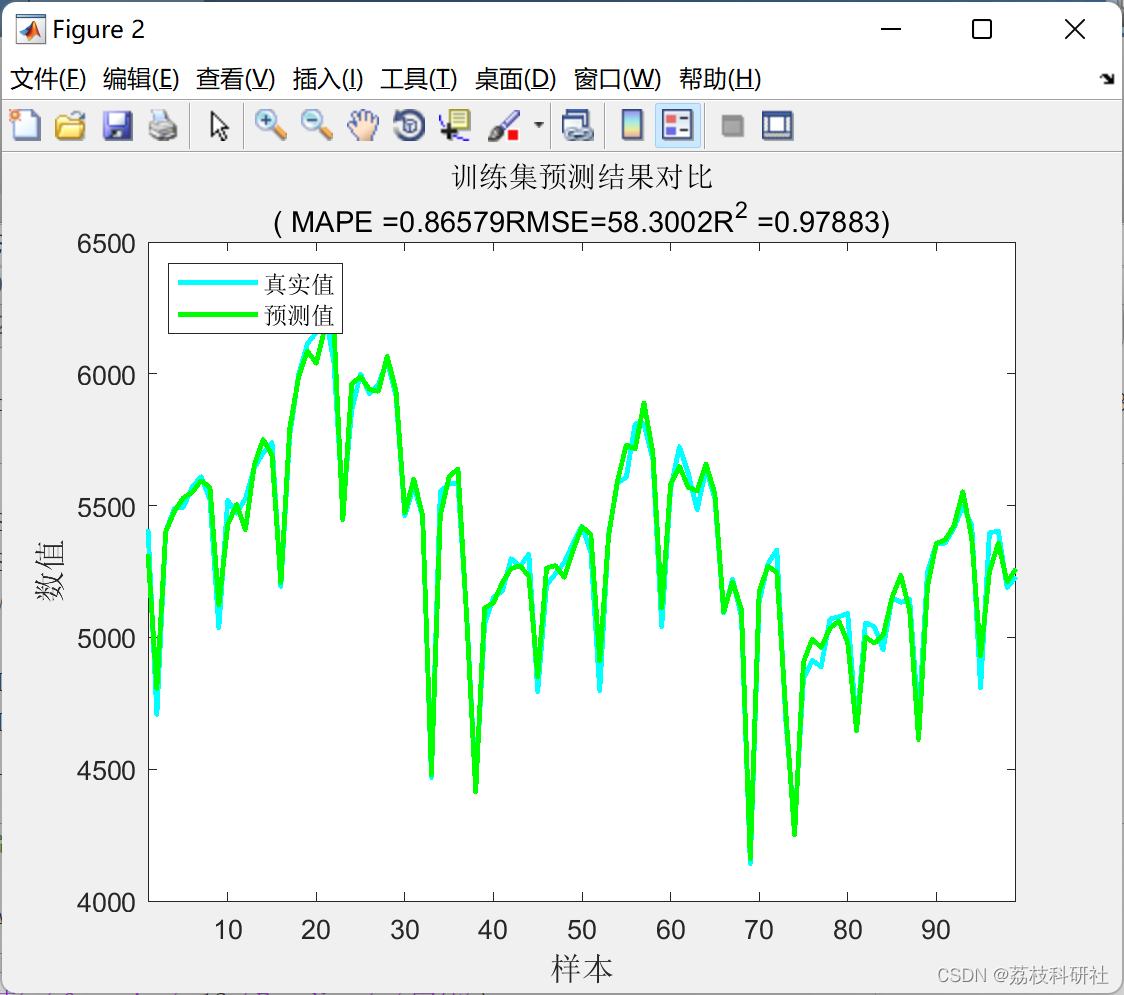
基于北方苍鹰算法优化LSTM(NGO-LSTM)研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Linux内核启动(理论,0.11版本)分段与分页
为什么要虚拟内存 我们知道,在之前上微机原理时,我们的程序是可以直接访问内存的,而且访问的是直接的物理内存,在实模式下,寄存器是16位的,数组总线(data bus)是16位的,…...

数据与C(字符串)
目录 一.概念引入 二.字符串(数组存储,必须以\0结尾) 三.错误示范 四.strlen()和sizeof()相对于字符串的不同 一.概念引入 “a”,a哪个是字符哪个又是字符串,嘿嘿不用猜了 我们在上一章中说过&#x…...

Python+Go实践(电商架构三)
文章目录服务发现集成consul负载均衡负载均衡算法实现配置中心nacos服务发现 我们之前的架构是通过ipport来调用的python的API,这样做的弊端是 如果新加一个服务,就要到某个服务改web(go)层的调用代码,配置IP/Port并发…...
基于 MySQL 排它锁实现分布式可重入锁解决方案
一、MySQL 排它锁和共享锁 在进行实验前,先来了解下MySQL 的排它锁和共享锁,在 MySQL 中的锁分为表锁和行锁,在行锁中锁又分成了排它锁和共享锁两种类型。 1. 排它锁 排他锁又称为写锁,简称X锁,是一种悲观锁&#x…...

【大数据】Hadoop-HA-Federation-3.3.1集群高可用联邦安装部署文档(建议收藏哦)
背景概述 单 NameNode 的架构使得 HDFS 在集群扩展性和性能上都有潜在的问题,当集群大到一定程度后,NameNode 进程使用的内存可能会达到上百 G,NameNode 成为了性能的瓶颈。因而提出了 namenode 水平扩展方案-- Federation。 Federation 中…...

【设计模式之美 设计原则与思想:面向对象】14 | 实战二(下):如何利用面向对象设计和编程开发接口鉴权功能?
在上一节课中,针对接口鉴权功能的开发,我们讲了如何进行面向对象分析(OOA),也就是需求分析。实际上,需求定义清楚之后,这个问题就已经解决了一大半,这也是为什么我花了那么多篇幅来讲…...

工作技术小结
2023/1/31 关于后端接口编写小结 1,了解小程序原型图流程和细节性的东西 2,数据库关联结构仔细分析,找到最容易查询的关键字段,标语表之间靠什么关联 2023/2/10 在web抓包过程中,如果要实现批量抓取,必须解…...
无重复字符的最长子串-力扣3-java
一、题目描述给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。示例 1:输入: s "abcabcbb"输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:输入: s "bbbbb"输出: 1解释: 因为…...
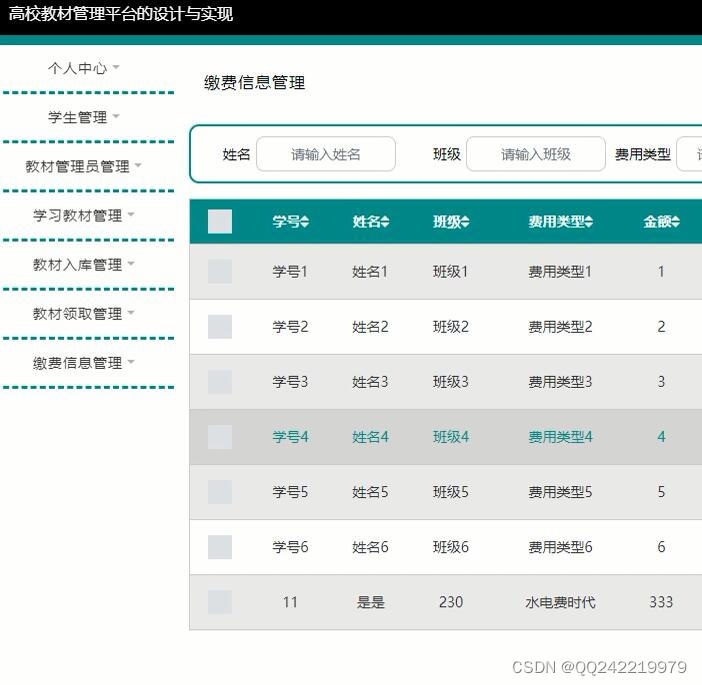
java ssm高校教材管理平台 idea maven
设计并且实现一个基于JSP技术的高校教材管理平台的设计与实现。采用MYSQL为数据库开发平台,SSM框架,Tomcat网络信息服务作为应用服务器。高校教材管理平台的设计与实现的功能已基本实现,主要学生、教材管理、学习教材、教材入库、教材领取、缴…...
【Python学习笔记】25.Python3 输入和输出(1)
前言 在前面几个章节中,我们其实已经接触了 Python 的输入输出的功能。本章节我们将具体介绍 Python 的输入输出。 输出格式美化 Python两种输出值的方式: 表达式语句和 print() 函数。 第三种方式是使用文件对象的 write() 方法,标准输出文件可以用…...
C++复习笔记8
泛型编程:编写的是与类型无关的通用代码,是代码复用的一种手段,模板是泛型编程的基础。 1.函数模板:类型参数化,增加代码复用性。例如对于swap函数,不同类型之间进行交换都需要进行重载,但是函数…...

RabbitMQ入门
目录1. 搭建示例工程1.1. 创建工程1.2. 添加依赖2. 编写生产者3. 编写消费者4. 小结需求 官网: https://www.rabbitmq.com/ 需求:使用简单模式完成消息传递 步骤: ① 创建工程(生成者、消费者) ② 分别添加依赖 ③ 编…...
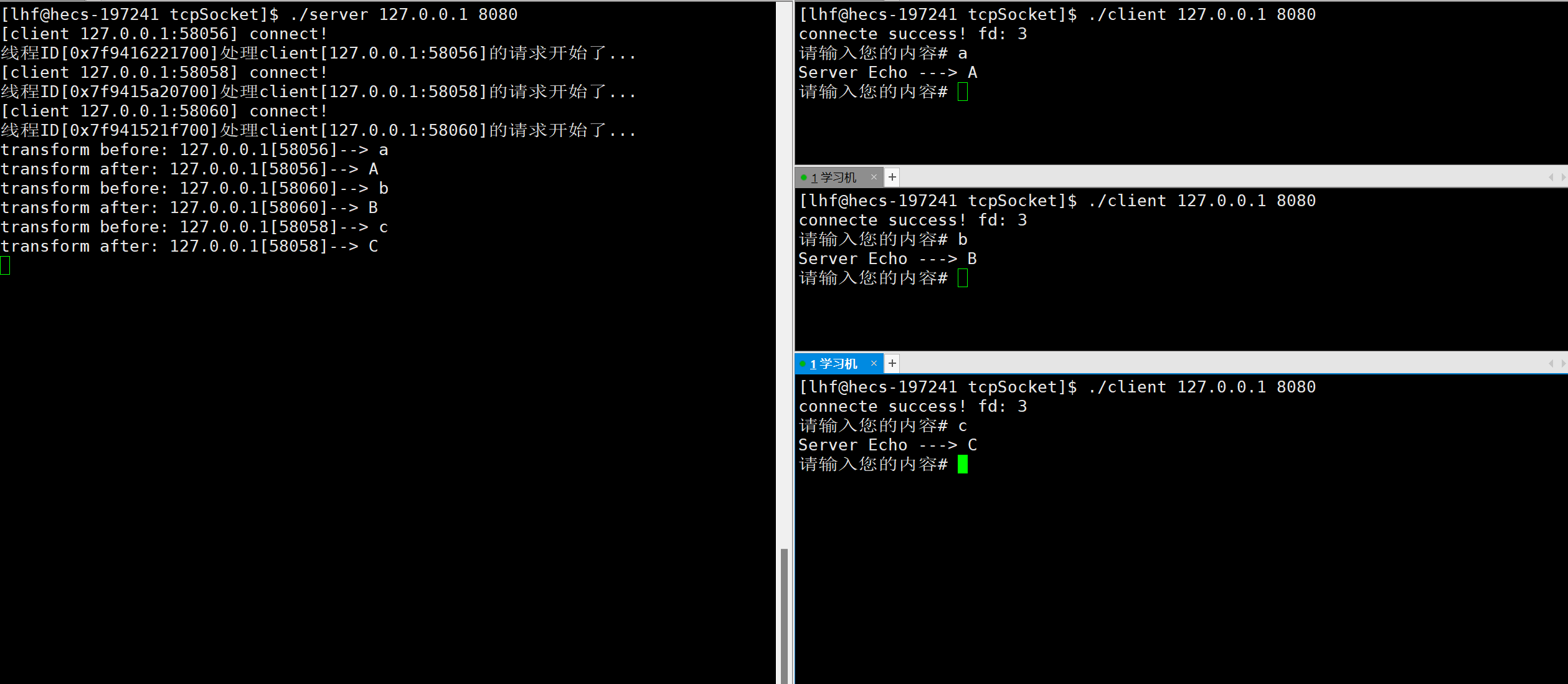
【计算机网络】Linux环境中的TCP网络编程
文章目录前言一、TCP Socket API1. socket2. bind3. listen4. accept5. connect二、封装TCPSocket三、服务端的实现1. 封装TCP通用服务器2. 封装任务对象3. 实现转换功能的服务器四、客户端的实现1. 封装TCP通用客户端2. 实现转换功能的客户端五、结果演示六、多进程版服务器七…...
idekCTF 2022 比赛复现
Readme 首先 []byte 是 go 语言里面的一个索引,比如: package mainimport "fmt"func main() {var str string "hello"var randomData []byte []byte(str)fmt.Println(randomData[0:]) //[104 101 108 108 111] }上面这串代码会从…...

jvm的类加载过程
加载 通过一个类的全限定名获取定义此类的二进制字节流将这个字节流所代表的静态存储结构转化为方法区的运行时数据结构在内存中生成一个代表这个类的java.lang.Class对象,作为方法区这个类的各种数据的访问入口链接 验证 验证内容的合法性准备 把方法区的静态变量初…...
VOC数据增强与调整大小
数据增强是针对数据集图像数量太少所采取的一种方法。 博主在实验过程中,使用自己的数据集时发现其数据量过少,只有280张,因此便想到使用数据增强的方式来获取更多的图像信息。对于图像数据,我们可以采用旋转等操作来获取更多的图…...

Linux 安装jenkins和jdk11
Linux 安装jenkins和jdk111. Install Jdk112. Jenkins Install2.1 Install Jenkins2.2 Start2.3 Error3.Awakening1.1 Big Data -- Postgres4. Awakening1. Install Jdk11 安装jdk11 sudo yum install fontconfig java-11-openjdk 2. Jenkins Install 2.1 Install Jenkins 下…...
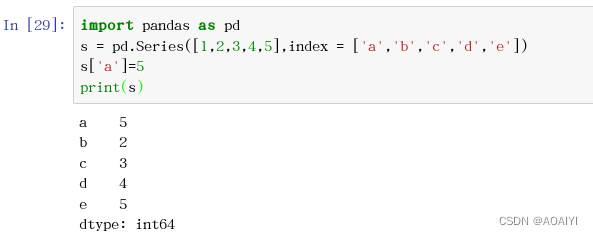
Pandas——Series操作【建议收藏】
pandas——Series操作 作者:AOAIYI 创作不易,觉得文章不错或能帮助到你学习,可以点赞收藏评论哦 文章目录pandas——Series操作一、实验目的二、实验原理三、实验环境四、实验内容五、实验步骤1.创建Series2.从具体位置的Series中访问数据3.使…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
