力扣每日一练(24-1-20)

大脑里的第一想法是排列组合,直接给出超级准确的最优解。
但不适用,hhh
只要连续的n个元素大于或者等于target就可以了
题目比自己想象的要好解决
解法是使用滑动窗口算法。这个算法的基本思想是维护一个窗口,使得窗口内的元素总和大于等于目标值,然后尝试缩小窗口以找到最小的满足条件的子数组。
Python
class Solution:def minSubArrayLen(self, target: int, nums: List[int]) -> int:n = len(nums)ans = n + 1start = 0end = 0total = 0while end < n:total += nums[end]while total >= target:ans = min(ans, end - start + 1)total -= nums[start]start += 1end += 1return 0 if ans == n + 1 else ansC#
public class Solution {public int MinSubArrayLen(int target, int[] nums) {int n = nums.Length;int ans = n + 1;int start = 0;int end = 0;int total = 0;while (end < n) {total += nums[end];while (total >= target) {ans = Math.Min(ans, end - start + 1);total -= nums[start];start++;}end++;}return ans == n + 1 ? 0 : ans;}
}解法的时间复杂度是O(n),因为每个元素最多被访问两次。
二分查找法
在这个问题中,O(n)的滑动窗口解法已经是最优解法,因为它只需要遍历一次数组。然而,如果你想要实现一个O(n log n)的解法,你可以使用二分查找的方法。这种方法的基本思想是先计算累积和数组,然后对每个累积和,使用二分查找找到最小的索引j,使得sum[j] - sum[i] >= target。
以下是这个方法的Python实现:
Python
import bisectclass Solution:def minSubArrayLen(self, target: int, nums: List[int]) -> int:n = len(nums)ans = n + 1sums = [0] * (n + 1)for i in range(1, n + 1):sums[i] = sums[i - 1] + nums[i - 1]for i in range(1, n + 1):to_find = target + sums[i - 1]bound = bisect.bisect_left(sums, to_find)if bound != len(sums):ans = min(ans, bound - (i - 1))return 0 if ans == n + 1 else ansC#
public class Solution {public int MinSubArrayLen(int target, int[] nums) {int n = nums.Length;int ans = n + 1;int[] sums = new int[n + 1];for (int i = 1; i <= n; i++) {sums[i] = sums[i - 1] + nums[i - 1];}for (int i = 1; i <= n; i++) {int to_find = target + sums[i - 1];int bound = Array.BinarySearch(sums, to_find);if (bound < 0) {bound = ~bound;}if (bound <= n) {ans = Math.Min(ans, bound - (i - 1));}}return ans == n + 1 ? 0 : ans;}
}相关文章:

力扣每日一练(24-1-20)
大脑里的第一想法是排列组合,直接给出超级准确的最优解。 但不适用,hhh 只要连续的n个元素大于或者等于target就可以了 题目比自己想象的要好解决 解法是使用滑动窗口算法。这个算法的基本思想是维护一个窗口,使得窗口内的元素总和大于等于目…...

Pytest系列(2) - assert断言详细使用
前言 与unittest不同,pytest使用的是python自带的assert关键字来进行断言assert关键字后面可以接一个表达式,只要表达式的最终结果为True,那么断言通过,用例执行成功,否则用例执行失败 assert小栗子 想在抛出异常之…...

CodeWave智能开发平台--03--目标:应用创建--10初级采购管理系统总结
摘要 本文是网易数帆CodeWave智能开发平台系列的第14篇,主要介绍了基于CodeWave平台文档的新手入门进行学习,实现一个完整的应用,本文主要完成10初级采购管理系统总结 CodeWave智能开发平台的14次接触 CodeWave参考资源 网易数帆CodeWave…...

外包干了4个月,技术退步明显.......
先说一下自己的情况,大专生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四年的功能测…...
图片批量建码怎么用?每张图片快速生成二维码
当我们需要给每个人分别下发对应的个人证件类图片信息,比如制作工牌、荣誉展示或者负责人信息展示时,现在都开始使用二维码的方法来展示员工信息。那么如何快速将每个人员的信息图片分别制作成二维码图片呢,最简单的方法就是使用图片批量建码…...

时间复杂度的排序
在计算机科学中,不同的算法有不同的时间复杂度。以下是一些常见的时间复杂度,并按照它们的增长速度从低到高排序: O(1) - 常数时间复杂度: 表示算法的执行时间是固定的,不随输入规模的增加而变化。例如,直接…...

js控制浏览器前进、后退、页面跳转
在JavaScript中,你可以使用 window 对象的 history 对象来控制浏览器的历史记录。以下是一些常用的方法: 前进和后退: window.history.forward(): 前进到历史记录中的下一个页面。window.history.back(): 返回历史记录中的上一个页面。window…...
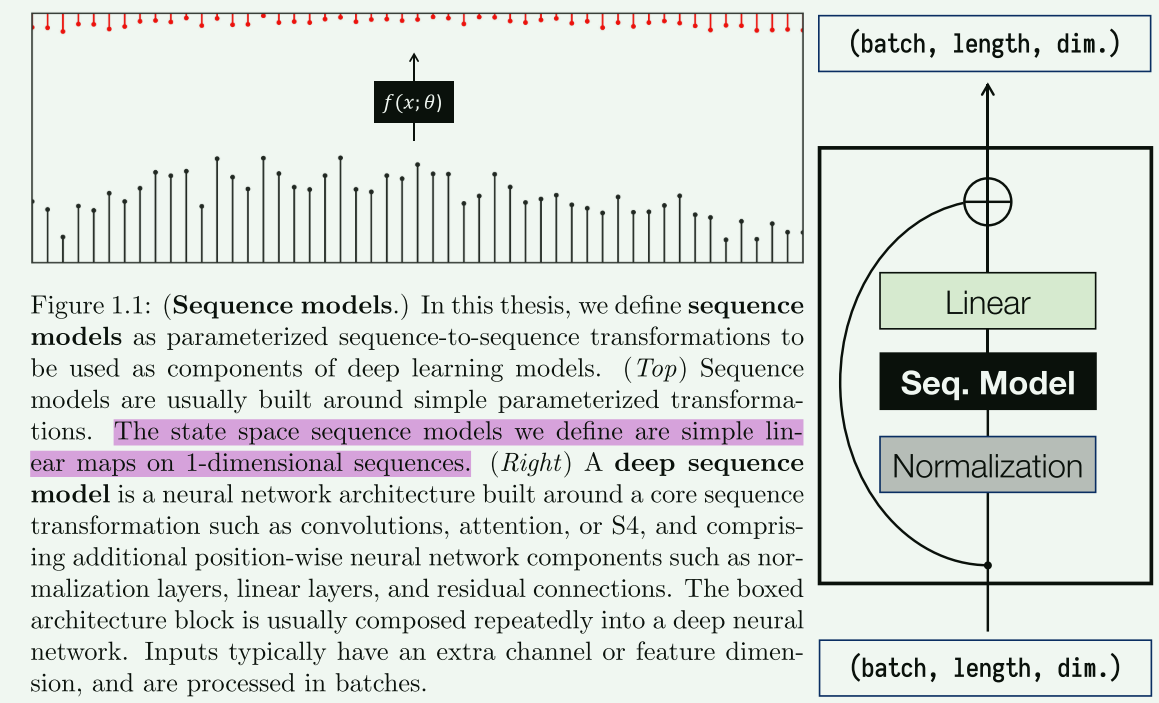
【长文阅读】MAMBA作者博士论文<MODELING SEQUENCES WITH STRUCTURED STATE SPACES>-Chapter1
Gu A. Modeling Sequences with Structured State Spaces[D]. Stanford University, 2023. 本文是MAMBA作者的博士毕业论文,为了理清楚MAMBA专门花时间拜读这篇长达330页的博士论文,由于知识水平有限,只能尽自己所能概述记录,并适…...
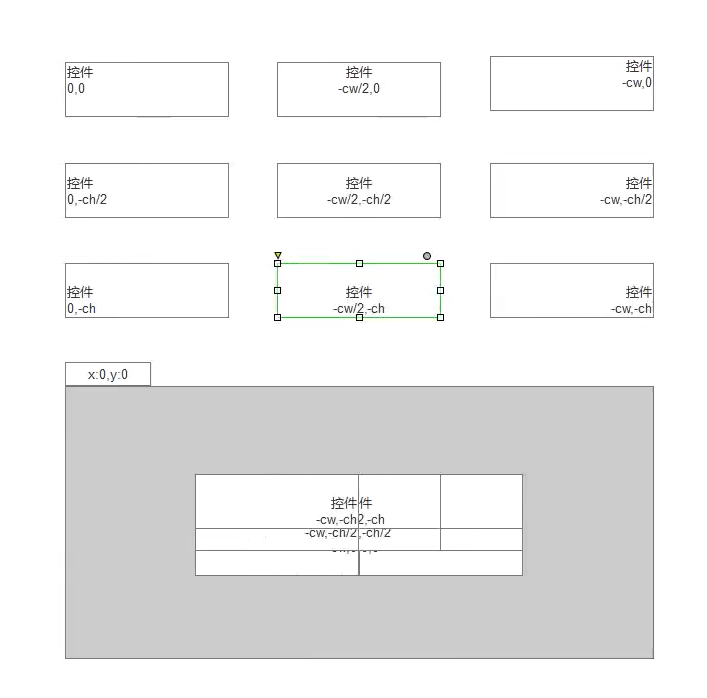
Unity3D学习之UI系统——GUI
文章目录 1. 前言2. 工作原理和主要作用3. 基础控件3.1 重要参数及文本和按钮3.1.1 GUI 共同点3.1.2 文本控件3.1.3 按钮控件 3.2 多选框和单选框3.2.1 多选框3.2.2 单选框3.2.3 输入框3.2.4 拖动条 3.3 图片绘制和框3.3.1 图片3.3.2 框绘制 4 工具栏和选择网格4.1 工具栏4.2 选…...

用户ssh正确密码登陆均报错Permission denied, please try again.处理方法
我的一台虚拟机IP是:192.168.59.133任何服务器使用任何用户ssh均报错,甚至连自己都不能ssh自己。 不能使用任何工具连接上该服务器 使用ssh连接自己的127.0.0.1和localhost都权限拒绝错误 ssh报错如下 任何服务器ssh报错内容均一样:报错内…...
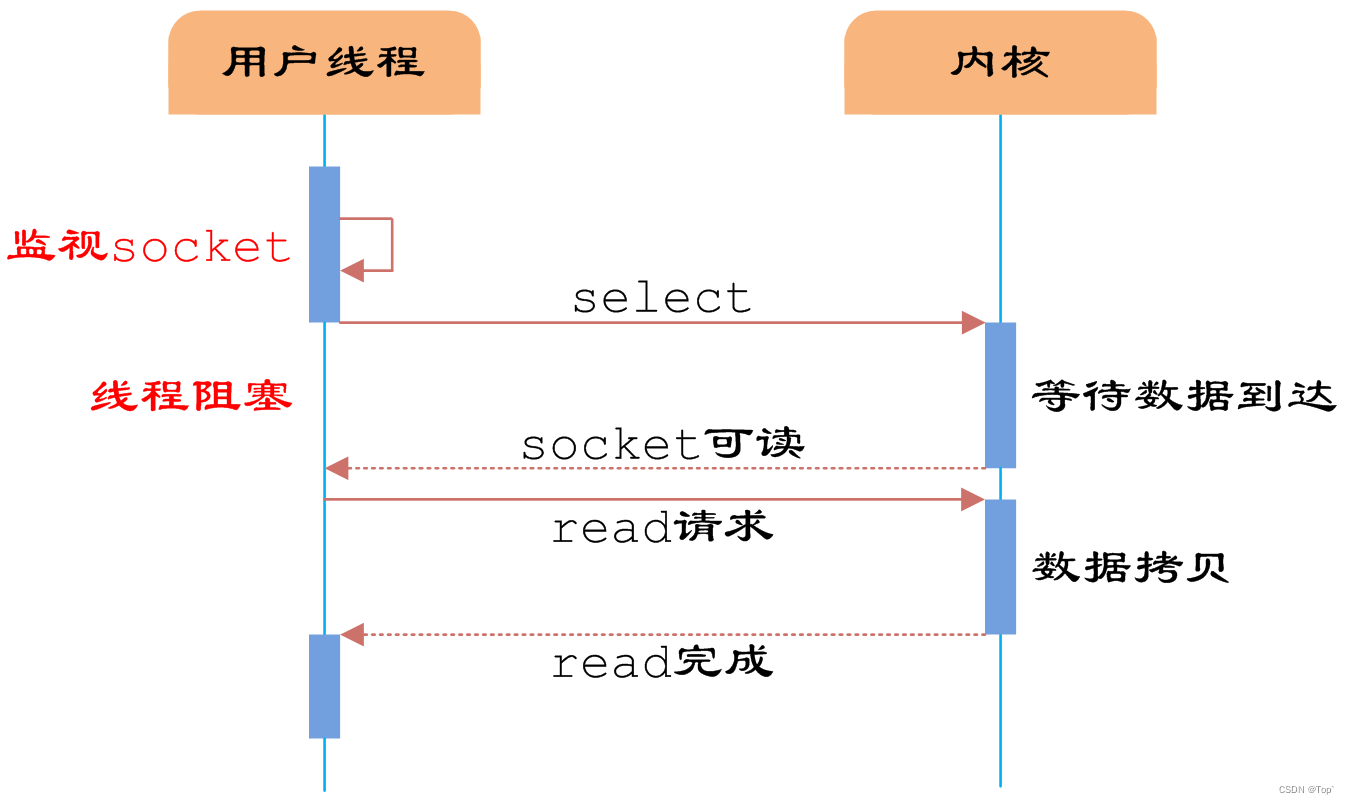
IO、NIO、IO多路复用
IO是什么? IO分为两类,它们之间是有区别的,而且有很大的区别;1. 文件系统的IO 也叫本地io,就是和磁盘或者外围存储设备进行读写操作,外围设备有USB、移动硬盘等等;2. 网络的IO 将数据发送给对方…...
探索FTP:原理、实践与安全优化
引言 在正式开始讲解之前,首先来了解一下文件存储的类型有哪些。 DAS、SAN和NAS是三种不同的存储架构,分别用于解决不同场景下的数据存储需求。 DAS (Direct Attached Storage 直接附加存储):DAS 是指将存储设备(如硬盘&#x…...
git中的语法和术语含义
目录 第一章、git常用术语1.1)文件状态1.2)git常用术语的含义 第二章、git文件状态解析2.1)从git init开始:Untracked(未跟踪)2.2)git add fileName后:Staged(已暂存&…...
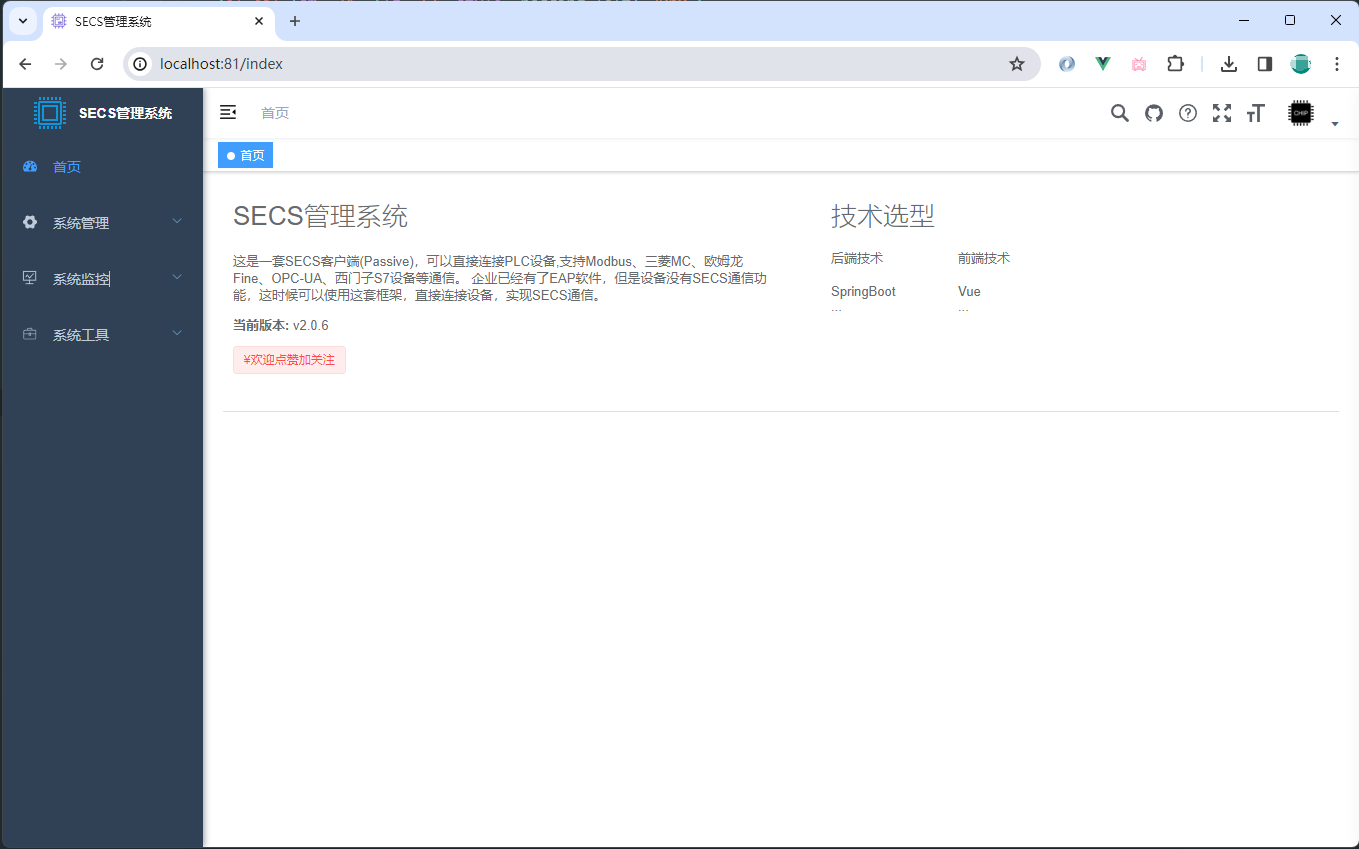
java SECS管理系统 将逐步推出 SECS 客户端(Passive) 管理系统 SECS快速开发平台 springboot secs开发平台
SECS管理系统 这是一套SECS客户端(Passive),可以直接连接PLC设备,支持Modbus、三菱MC、欧姆龙Fine、OPC-UA、西门子S7设备等通信。 企业已经有了EAP软件,但是设备没有SECS通信功能,这时候可以使用这套框架,直接连接设备ÿ…...

使 a === 1 a === 2 a === 3 为 true 的几种“下毒“方法
前言 这算得上是近些年的前端网红题了,曾经对这种网红题非常抵触,认为非常没有意义。 看到了不少人有做分享,有各种各样的方案,有涉及到 JS 非常基础的知识点,也不得不感叹解题者的脑洞之大。 但是,拿来…...
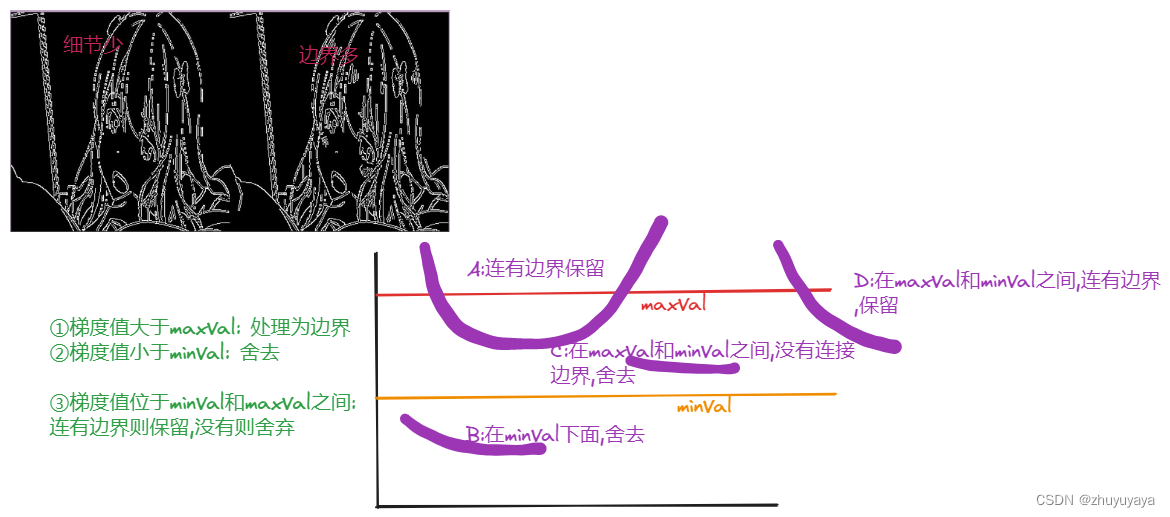
Canny边缘检测 双阈值检测理解
问题引入 我们用一个实际例子来引入问题 import cv2 import numpy as npimgcv2.imread("test.png",cv2.IMREAD_GRAYSCALE) # 修改图像大小 show cv2.resize(img,(500,500))v1cv2.Canny(show,120,250) v2cv2.Canny(show,50,100)# 连接图像 res np.hstack((v1,v2)…...

自动化测试:5分钟了解Selenium以及如何提升自动化测试的效果
在快节奏的技术世界里,自动化测试已经成为确保 Web 应用程序质量和性能的重要手段。自动化测试不仅加快了测试过程,还提高了测试的重复性和准确性。Selenium,作为领先的自动化测试工具之一,为测试人员提供了强大的功能来模拟用户在…...
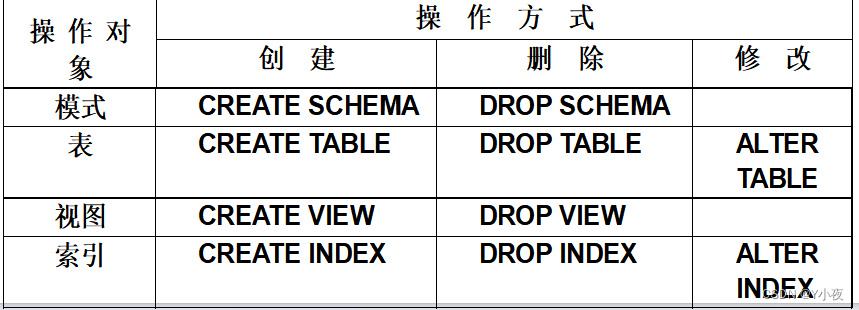
【MySQL】——关系数据库标准语言SQL(大纲)
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...

力扣hot100 最长有效括号 动态规划
Problem: 32. 最长有效括号 文章目录 思路Code 思路 👨🏫 参考题解 Code ⏰ 时间复杂度: O ( n ) O(n) O(n) 🌎 空间复杂度: O ( n ) O(n) O(n) class Solution {public int longestValidParentheses(String s){int n s.length();…...

@RequestBody注解基础
RequestBody RequestBody注解一般与post方法使用。 一个请求中只能存在一个RequestBody注解。 RequestBody 用于接收前端传递给后端的json字符串中的数据。(处理json格式的数据) 语法格式: (RequestBody Map map) (RequestBody Object obje…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
