位运算相关
文章目录
- 一、求1的个数
- 二、另类加法
- 三、数组中出现一次的数字
- 四、数组中出现一次的数字变形
一、求1的个数
二进制中1的个数
法一:逐位判断
根据与&运算 n&1=0,说明n的最右边一位为0 n&1=1,说明n的最右边一位为1
所以思路就是,将n右移再与1按位与
class Solution {
public:int hammingWeight(uint32_t n) {int count=0;while(n){if((n&1)==1) count++;n=n>>1;}return count;}
};
时间复杂度:O(logn)
逐位判断需循环log2n次,其中log2n代表数字n最高位1的所在位数(例如log2 4 = 2,log2 16 = 4)
右移一位的操作相当于除2
空间复杂度:O(1)
法二:利用n&(n-1)
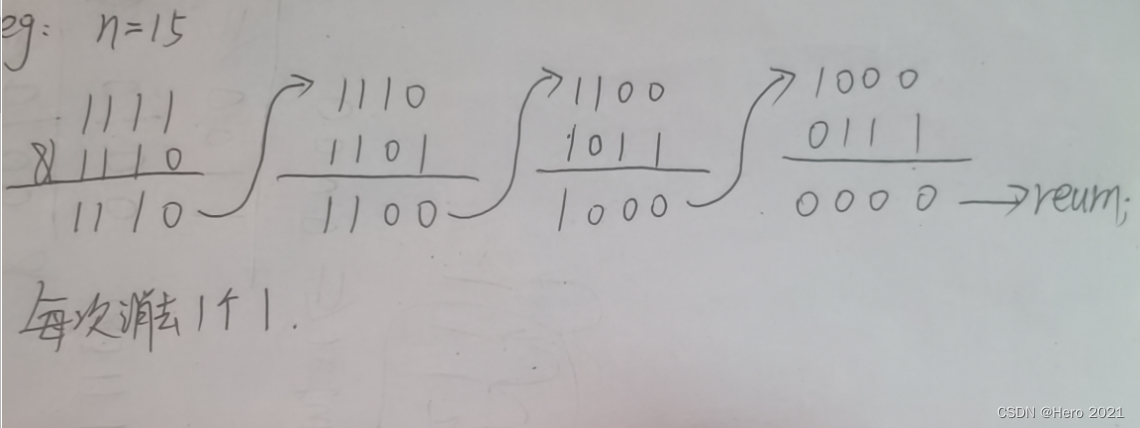
class Solution {
public:int hammingWeight(uint32_t n) {int count=0;while(n){n=n&n-1;count++;}return count;}
};
时间复杂度:O(m) m为二进制中1的个数
空间复杂度:O(1)
二、另类加法
不用加减号的加法
与:同时为1,才为1
异或:相同为0,相异为1

class Solution {
public:int add(int a, int b) {
//因为不允许用+号,所以求出异或部分和进位部分依然不能用+ 号,所以只能循环到没有进位为止 while(b!=0){
//保存进位值,下次循环用int c=(unsigned int)(a&b)<<1;//C++中负数不支持左移位,因为结果是不定的
//保存不进位值,下次循环用,a^=b;
//如果还有进位,再循环,如果没有,则直接输出没有进位部分即可。b=c; }return a;}
};
/*
把a+b转换成非进位和+进位,由于不能用加法,因此要一直转换直到第二个加数变成0。
用递归的写法比循环更容易一下子看懂
*/
class Solution {public int add(int a, int b) {if (b == 0) {return a;}// 转换成非进位和 + 进位return add(a ^ b, (a & b) << 1);}
};
三、数组中出现一次的数字
传送门
class Solution {
public:vector<int> singleNumbers(vector<int>& nums) {int res=0;//相同取0,相异取1,因此0^0=0,0^1=1,0异或任何数都为本身,可理解为没影响for (int n: nums) {res ^=n;//假设两个只出现一次的数分别为a和b,获得a异或b的结果}//找到ab第一个不相同的二进制位,用位与&操作(两个都为1才为1,其余为0,因此可理解0和任何数相与都还是本身)//理解:位与,就是0可以掩盖掉所有数字,0遇0为0,遇1还为0(子网掩码)//通过1的位置变化找出首个不一样的二进制位int m=1;while((m&res)==0){//m=000001,当第一位不是1时,结果为0,则m左移一位,000010类推直到找出m<<=1;}//找到m以后,用m划分数组,两个相同的数字,在m位一定相同,即其与m位与的结果一定是相同的,因此按m&n==0划分,就一定能保证://(1)原来相同的元素还在一组//(2)不同的两个元素被分到了不同组int a=0,b=0;for (int n:nums) {if ((n&m)==0) a^=n;else b^=n;}return {a,b};}
};
四、数组中出现一次的数字变形
传送门
法一:哈西最简单的方法
class Solution {
public:int singleNumber(vector<int>& nums) {map<int,int> m;for(auto e: nums){m[e]++;}for(auto e: m){if(e.second==1) return e.first;}return 0;}
};
法二:位运算
7 : 0B0111 7 : 0B01117 : 0B0111^^^|||出现数 333 // 从上向下,可以发现[3个7]每位都出次了 3 次那这样时再增加一个数。7 : 0B0111 7 : 0B01117 : 0B01114 : 0B0100^^^|||出现数 433 // 从上向下,只有第 3位bit 出现了 4次%%%333 // 接下来,把现各个位出现的次数,按 3取余‖‖‖100 // 取余结果刚好100对应的就是4
class Solution {
public:int singleNumber(vector<int>& nums) {int res = 0;for (int i = 0, sub = 0; i < 32; ++i, sub = 0) {for (auto &n : nums) sub += ((n >> i) & 1);if (sub % 3) res |= (1 << i);}return res;}
};
相关文章:

位运算相关
文章目录一、求1的个数二、另类加法三、数组中出现一次的数字四、数组中出现一次的数字变形一、求1的个数 二进制中1的个数 法一:逐位判断 根据与&运算 n&10,说明n的最右边一位为0 n&11,说明n的最右边一位为1 所以思路就是&…...

Linux进程信号(产生、保存、处理)/可重入函数概念/volatile理解/SIGCHLD信号
首先区分一下Linux信号跟进程间通信中的信号量,它们的关系就犹如老婆跟老婆饼一样,没有一毛钱的关系。 信号的概念 信号的概念:信号是进程之间事件异步通知的一种方式,属于软中断。比如:红绿灯是一种信号,…...

锯齿数组 - 贪心
文章目录锯齿数组 -贪心(不过挺像滑动窗口的)1144. 递减元素使数组呈锯齿状锯齿数组 -贪心(不过挺像滑动窗口的) 1144. 递减元素使数组呈锯齿状 题目链接:1144. 递减元素使数组呈锯齿状 题目大意:给你一个…...

[CVPR 2022] Balanced Contrastive Learning for Long-Tailed Visual Recognition
Contents IntroductionMethodPreliminariesBalanced Contrastive Learning (BCL)Drawbacks of SCLClass-averagingClass-complementLower bound of BCLOptimization with Logit CompensationFrameworkExperimentReferencesIntroduction 作者发现对于在长尾数据集上,Supervised…...

23种设计模式-工厂模式
工厂模式是一种创建型设计模式,它提供了一种创建对象的方式,而无需将具体的对象创建逻辑暴露给客户端。在Java中,工厂模式常常用于创建复杂对象或对象的构造过程涉及到多个步骤的情况。 在Android开发中,工厂模式也经常被使用&am…...

Linux操作系统学习(进程等待)
文章目录进程等待进程等待的必要性如何进程等待waiwaitpid验证进程等待 我们知道fork函数可以创建一个子进程,而子进程通常是替父进程完成一些任务,而父进程在fork之后需要通过wait/waitpid等待子进程退出。这就是进程等待 进程等待的必要性 通过获…...
load 和 import 命令的区别)
Docker学习(十八)load 和 import 命令的区别
Docker 中有两个命令可以将本地文件系统中的 tar 文件导入到 Docker 中:docker load 和 docker import。尽管它们的作用类似,但它们之间有一些重要的区别。 1.使用方式的不同: docker load 的使用示例: docker load --input tes…...

mysql中的事务
在日常生活中,我们会遇到一个场景,那就是在转账的时候,A有1000块钱,要给B转账500,那么最后的结果是A有500,B有500,但是也有可能出现A没有钱了,B有1000块,或者在转账过程中卡顿,这是不符合逻辑的,那么这个时候就要使用事务来解决问题 事务就是把一堆sql语句打包成一个整体,要么…...
)
《C++ Primer Plus》第18章:探讨 C++ 新标准(9)
编程练习 下面是一个简短程序的一部分: int main() {using namespace std;// list of double deduced from list contentsauto q average_list ({15.4, 10.7, 9.0});cout << q << endl;// list of int deduced from list contentscout << averag…...

记录一次PWM信号异常问题
问题我使用单片机输出PWM控制机械臂,但是控制过程中,机械臂总是会出现莫名的抽动。利用示波器测试PWM信号,发现信号正常。过程(1)在反复的测试过程中,队友提出,将示波器的地线放在左侧的GND波形…...

简单了解---性能测试
目录 一、什么是性能测试 二、常见的性能测试指标 1、并发 2、响应时间 3、事务 4、点击率 5、吞吐量 6、资源利用率 三、性能测试的分类 1、一般测试 2、负载测试 3、压力测试 4、稳定性测试 四、为什么要做性能测试? 五、影响性能的因素有哪些&…...
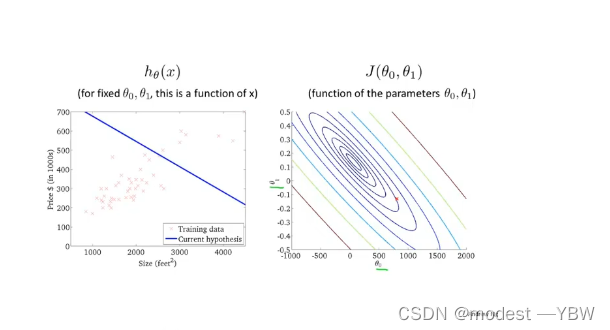
1.机器学习笔记第一周
机器学习利用领域: 1:随着网络数据增大,需要搜集用户的数据,做喜好性偏向判断等。 2:只要有数据的,无论是医疗领域,还是基因领域都是需要机器学习来发现数据密码。 3:机器自我学习…...
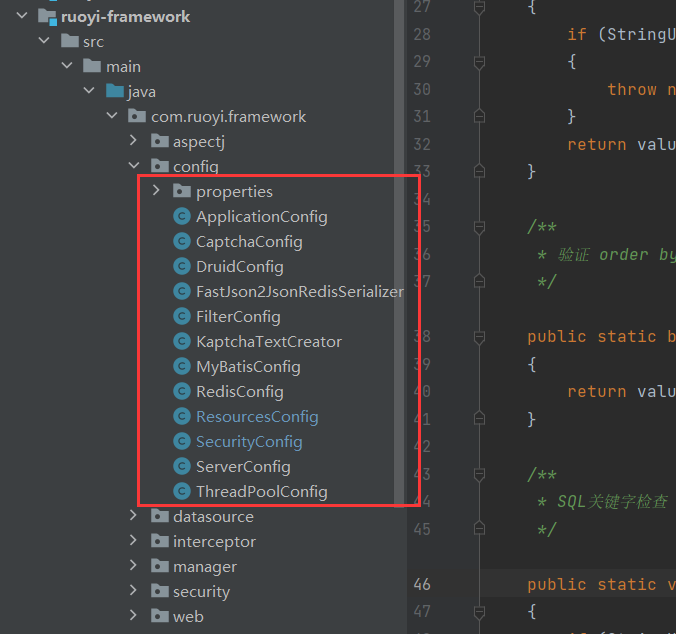
若依学习(前后端分离版)——启动时发生了啥?(@PostConstruct)(mybatis log free)
我们可以发现若依启动时执行了一些sql我们可以安装一个插件mybatis log free 来更好的进行sql查看 ,安装后需要修改一下若依的日志配置如下查看日志,我们发现执行了三个方法(),分别查询了一些数据。以第二个方法为例子…...

每日十问9c++-内存模型和名称空间
每日十问9c内存模型和名称空间 1.对于下面的情况,应使用哪种存储方案? a.homer 是函数的形参。 b. secret变量由两个文件共享。 c.topsecret 变量由一个文件中的所有函数共享,但对于其他文件来说是隐藏的。 d. beencalled 记录包含它的函数被调用的次数…...

【python】JSON数据类型与Python数据类型之间的转化
注:最后有面试挑战,看看自己掌握了吗 文章目录JSON格式文件JSON格式序列化与反序列化作用JSON常用数据结构键值对的集合值的有序列表JSON数据类型与Python数据类型之间的转化JSON格式和python的区别读写json文件dump 把python 写到json文件load 把json写…...

Spring——什么是事务?传播行为?事务隔离级别有哪些?
思维导图一、什么是事务?多条DML要么同时成功,要么同时失败Transaction(tx)二、事务的四个过程:开启事务(start transaction)执行核心业务代码提交事务(如果核心业务处理过程中没有出…...
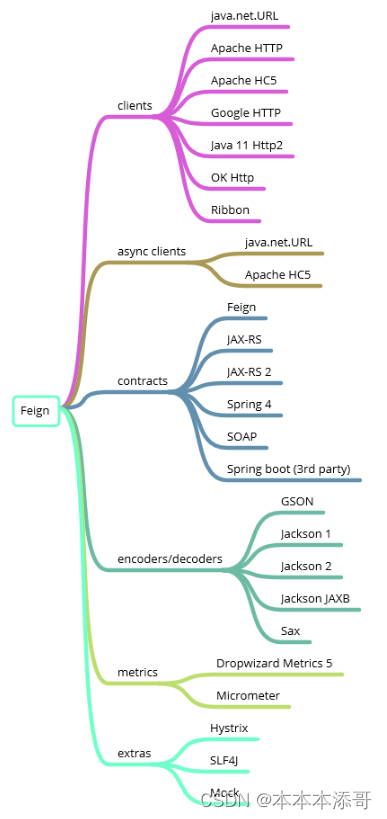
【项目实战】使用Feign服务间相互调用,其实OpenFeign也没有想象中那么难嘛
一、Feign介绍 openfeign是一个java的http客户端,用来简化http调用 二、Feign架构(来自官方) Feign由五大部分组成, 由于刚开始接触 feign ,比较关注的 clients 跟 encoders/decoders 三、OKHTTP与Feign之间的关系 在Feign中,Client是一个非常重要的组件,Feign最终…...
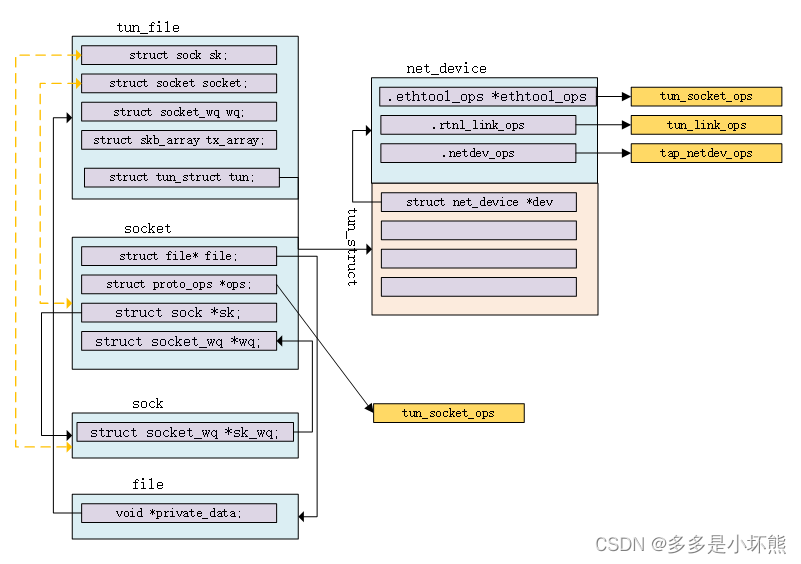
tun驱动之ioctl
struct ifreq ifr; ifr.ifr_flags | IFF_TAP | IFF_NO_PI; ioctl(fd, TUNSETIFF, (void *)&ifr); 上面的代码的意思是设置网卡信息,并将tun驱动设置为TAP模式。在TAP模式下,在用户空间下调用open打开/dev/net/tun驱动文件,发送(调用send函…...
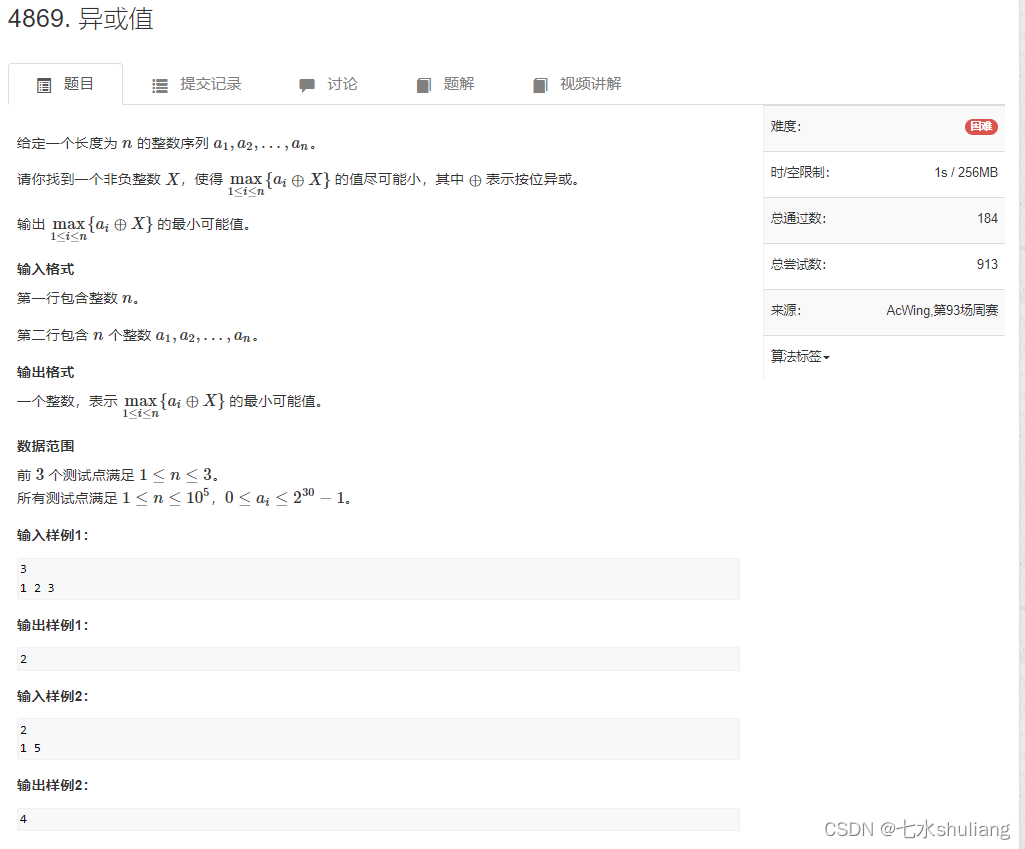
[acwing周赛复盘] 第 93 场周赛20230304
[acwing周赛复盘] 第 93 场周赛20230304 一、本周周赛总结二、 4867. 整除数1. 题目描述2. 思路分析3. 代码实现三、 4868. 数字替换1. 题目描述2. 思路分析3. 代码实现四、4869. 异或值1. 题目描述2. 思路分析3. 代码实现六、参考链接一、本周周赛总结 彩笔了,只A…...

NOIP2022 T4 比赛
P8868 [NOIP2022] 比赛 题目大意 有两个长度为nnn的序列aaa和bbb,有qqq次询问,每次询问给出l,rl,rl,r,求 ∑ilr∑ji1r(maxkijak)(maxlijbl)\sum\limits_{il}^r\sum\limits_{ji1}^r(\max\limits_{ki}^ja_k)\times(\max\limits_{li}^jb_l…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...
