NOIP2022 T4 比赛
P8868 [NOIP2022] 比赛
题目大意
有两个长度为nnn的序列aaa和bbb,有qqq次询问,每次询问给出l,rl,rl,r,求
∑i=lr∑j=i+1r(maxk=ijak)×(maxl=ijbl)\sum\limits_{i=l}^r\sum\limits_{j=i+1}^r(\max\limits_{k=i}^ja_k)\times(\max\limits_{l=i}^jb_l)i=l∑rj=i+1∑r(k=imaxjak)×(l=imaxjbl)
题解
我们可以离线做,对所有询问按rrr从小到大排序。假设当前考虑到rrr,令xi=maxj=irajx_i=\max\limits_{j=i}^ra_jxi=j=imaxraj,yi=maxj=irbjy_i=\max\limits_{j=i}^rb_jyi=j=imaxrbj,我们可以用线段树维护vi=∑j=irxjyjv_i=\sum\limits_{j=i}^rx_jy_jvi=j=i∑rxjyj,那么对于每一次询问,答案就是∑i=lrvi\sum\limits_{i=l}^rv_ii=l∑rvi。
可以先用单调栈处理出a,ba,ba,b数组中每个元素作为最大值向左能覆盖的最大位置,那么对于每一个询问的rrr,我们将当前右端点不断移动直到到达rrr点,每一次移动都要对线段树进行以下三个操作:
- 区间更新这一段的xix_ixi为ara_rar
- 区间更新这一段的yiy_iyi为brb_rbr
- 让下标在111到rrr之间的每一个viv_ivi都加上xi×yix_i\times y_ixi×yi。
线段树一共要维护四个信息,sss表示fif_ifi的区间和,xyxyxy表示xi×yix_i\times y_ixi×yi的区间和,xxx表示xix_ixi的区间和,yyy表示yiy_iyi的区间和。
有六个懒标记,cx,cycx,cycx,cy是覆盖标记,lyxy,lyx,lyy,lyvly_{xy},ly_x,ly_y,ly_vlyxy,lyx,lyy,lyv分别是∑xiyi,∑x,∑y,∑1\sum x_iy_i,\sum x,\sum y,\sum 1∑xiyi,∑x,∑y,∑1(即区间长度)的增量,也就是增加的倍数。
在下传懒标记时,按照是否有被覆盖,要做一些处理:
- 如果x,yx,yx,y都被覆盖,则lyxy∑xiyi=lyxy×cx×cy×lenly_{xy}\sum x_iy_i=ly_{xy}\times c_x\times c_y\times lenlyxy∑xiyi=lyxy×cx×cy×len,将lyxy×cx×cyly_{xy}\times c_x\times c_ylyxy×cx×cy加到lycly_clyc中
- 如果xxx被覆盖,则lyxy∑xiyi=lyxy×cx×∑yily_{xy}\sum x_iy_i=ly_{xy}\times c_x\times \sum y_ilyxy∑xiyi=lyxy×cx×∑yi,lyx∑xi=lyx×cx×lenly_x\sum x_i=ly_x\times c_x\times lenlyx∑xi=lyx×cx×len,将lyxy×cxly_{xy}\times c_xlyxy×cx加到lyyly_ylyy中,将lyx×cxly_x\times c_xlyx×cx加到lycly_clyc中
- 如果yyy被覆盖,与xxx被覆盖类似
- 如果都没有被覆盖,则各自相加即可
更新完加操作后,再更新覆盖操作。
对于区间信息的更新,首先s+=lyxy×∑xiyi+lyx×∑xi+lyy×∑yi+lyc×∑1s+=ly_{xy}\times \sum x_iy_i+ly_x\times \sum x_i+ly_y\times \sum y_i+ly_c\times \sum 1s+=lyxy×∑xiyi+lyx×∑xi+lyy×∑yi+lyc×∑1,其余部分要根据被覆盖的情况来更新。
对于取模的问题,用unsigned long long自然溢出即可解决。
可以看代码帮助理解。
时间复杂度为O(nlogn+qlogn)O(n\log n+q\log n)O(nlogn+qlogn)。
code
#include<bits/stdc++.h>
#define lc k<<1
#define rc k<<1|1
using namespace std;
typedef unsigned long long ULL;
const int N=250005;
int tt,n,q,q1[N],q2[N],l1[N],l2[N];
ULL a[N],b[N],ans[N];
struct gt{int l,r,id;
}w[N];
struct node{ULL s,xy,x,y;
}tr[N*4];
struct tag{ULL cx,cy,xy,x,y,c;
}ly[N*4];
bool cmp(gt ax,gt bx){return ax.r<bx.r;
}
void up(int k){tr[k]=(node){tr[lc].s+tr[rc].s,tr[lc].xy+tr[rc].xy,tr[lc].x+tr[rc].x,tr[lc].y+tr[rc].y};
}
void gx(int k,int len,tag t){tag &v1=ly[k];if(v1.cx&&v1.cy){v1.c+=t.xy*v1.cx*v1.cy+t.x*v1.cx+t.y*v1.cy+t.c;}else if(v1.cx){v1.c+=t.x*v1.cx+t.c;v1.y+=t.xy*v1.cx+t.y;}else if(v1.cy){v1.c+=t.y*v1.cy+t.c;v1.x+=t.xy*v1.cy+t.x;}else{v1.xy+=t.xy;v1.x+=t.x;v1.y+=t.y;v1.c+=t.c;}if(t.cx) v1.cx=t.cx;if(t.cy) v1.cy=t.cy;node &v2=tr[k];v2.s+=t.xy*v2.xy+t.x*v2.x+t.y*v2.y+t.c*len;if(t.cx&&t.cy){v2.xy=t.cx*t.cy*len;v2.x=t.cx*len;v2.y=t.cy*len;}else if(t.cx){v2.xy=t.cx*v2.y;v2.x=t.cx*len;}else if(t.cy){v2.xy=t.cy*v2.x;v2.y=t.cy*len;}
}
void down(int k,int l,int r){if(ly[k].cx||ly[k].cy||ly[k].xy||ly[k].x||ly[k].y||ly[k].c){int mid=l+r>>1;gx(lc,mid-l+1,ly[k]);gx(rc,r-mid,ly[k]);ly[k]=(tag){0,0,0,0,0,0};}
}
void ch(int k,int l,int r,int x,int y,tag t){if(l>=x&&r<=y){gx(k,r-l+1,t);return;}down(k,l,r);int mid=l+r>>1;if(x<=mid) ch(lc,l,mid,x,y,t);if(y>mid) ch(rc,mid+1,r,x,y,t);up(k);
}
ULL find(int k,int l,int r,int x,int y){if(l>=x&&r<=y) return tr[k].s;down(k,l,r);int mid=l+r>>1;ULL re=0;if(x<=mid) re+=find(lc,l,mid,x,y);if(y>mid) re+=find(rc,mid+1,r,x,y);return re;
}
int main()
{scanf("%d%d",&tt,&n);a[0]=b[0]=1e9;q1[++q1[0]]=q2[++q2[0]]=0;for(int i=1;i<=n;i++){scanf("%llu",&a[i]);while(q1[0]&&a[i]>a[q1[q1[0]]]) --q1[0];l1[i]=q1[q1[0]]+1;q1[++q1[0]]=i;}for(int i=1;i<=n;i++){scanf("%llu",&b[i]);while(q2[0]&&b[i]>b[q2[q2[0]]]) --q2[0];l2[i]=q2[q2[0]]+1;q2[++q2[0]]=i;}scanf("%d",&q);for(int i=1;i<=q;i++){scanf("%d%d",&w[i].l,&w[i].r);w[i].id=i;}sort(w+1,w+q+1,cmp);for(int i=1,r=0;i<=q;i++){while(r<w[i].r){++r;ch(1,1,n,l1[r],r,(tag){a[r],0,0,0,0,0});ch(1,1,n,l2[r],r,(tag){0,b[r],0,0,0,0});ch(1,1,n,1,r,(tag){0,0,1,0,0,0});}ans[w[i].id]=find(1,1,n,w[i].l,w[i].r);}for(int i=1;i<=q;i++){printf("%llu\n",ans[i]);}return 0;
}
相关文章:

NOIP2022 T4 比赛
P8868 [NOIP2022] 比赛 题目大意 有两个长度为nnn的序列aaa和bbb,有qqq次询问,每次询问给出l,rl,rl,r,求 ∑ilr∑ji1r(maxkijak)(maxlijbl)\sum\limits_{il}^r\sum\limits_{ji1}^r(\max\limits_{ki}^ja_k)\times(\max\limits_{li}^jb_l…...
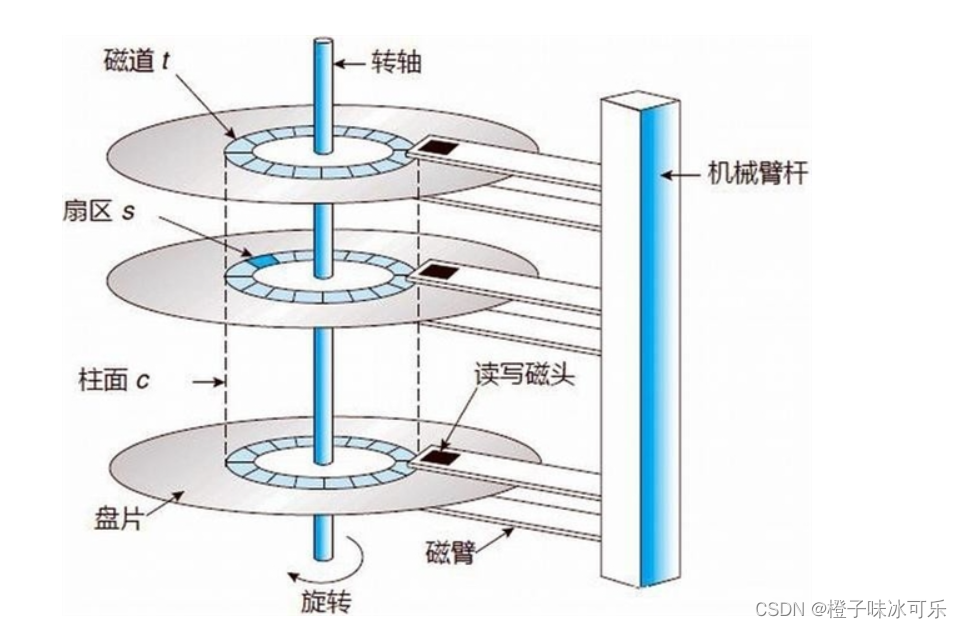
计算机组成原理
目录 ❤ 控制器 ❤ 运算器 ❤ 控制器运算器(计算机的中央处理器CPU) ❤ 存储器 内存(主存) 外存 内存和外村的区别 ❤ 输入设备 ❤ 输出设备 ❤ 适配器 ❤ 总线 ❤ 启动计算机的流程 ❤ 机械硬盘 ❤ 固态硬盘 python从小白到总裁完整教程目录:https://b…...

1. 命名规范
1. 命名规范 成绩10开启时间2021年09月17日 星期五 18:00折扣0.8折扣时间2021年11月6日 星期六 00:00允许迟交否关闭时间2021年11月21日 星期日 00:00 家有家法,行有行规。在家有家的规矩,入行有行的规矩。我们计算机一行就有一个命名的规矩,…...

论文投稿指南——中文核心期刊推荐(新闻事业)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
【Linux】工具(4)——make/Makefile
本期博客我们的任务就是搞懂自动化构建工具——make/Makefile一、什么是make/Makefile📌make是一个命令工具,是一个解释makefile中指令的命令工具,一般来说,大多数的IDE都有这个命令,比如:Delphi的make&…...
【企业服务器LNMP环境搭建】nginx安装
1、介绍(官方网址:nginx news ) 1.1 常见用法 1) web服务器软件 httpd http协议 同类的web服务器软件:apache nginx(俄罗斯) IIS(微软 fastcgi) lighttpd(德国) 2)代理服务器 反向代理 3)邮箱代理服务器 IMAP POP3 SMTP 4)负载均…...

Linux 配置规范 操作系统 _S3A3G3
目录 1.检查使用IP协议远程维护的设备是否配置SSH协议,禁用telnet协议 2.检查账户认证失败次数限制...
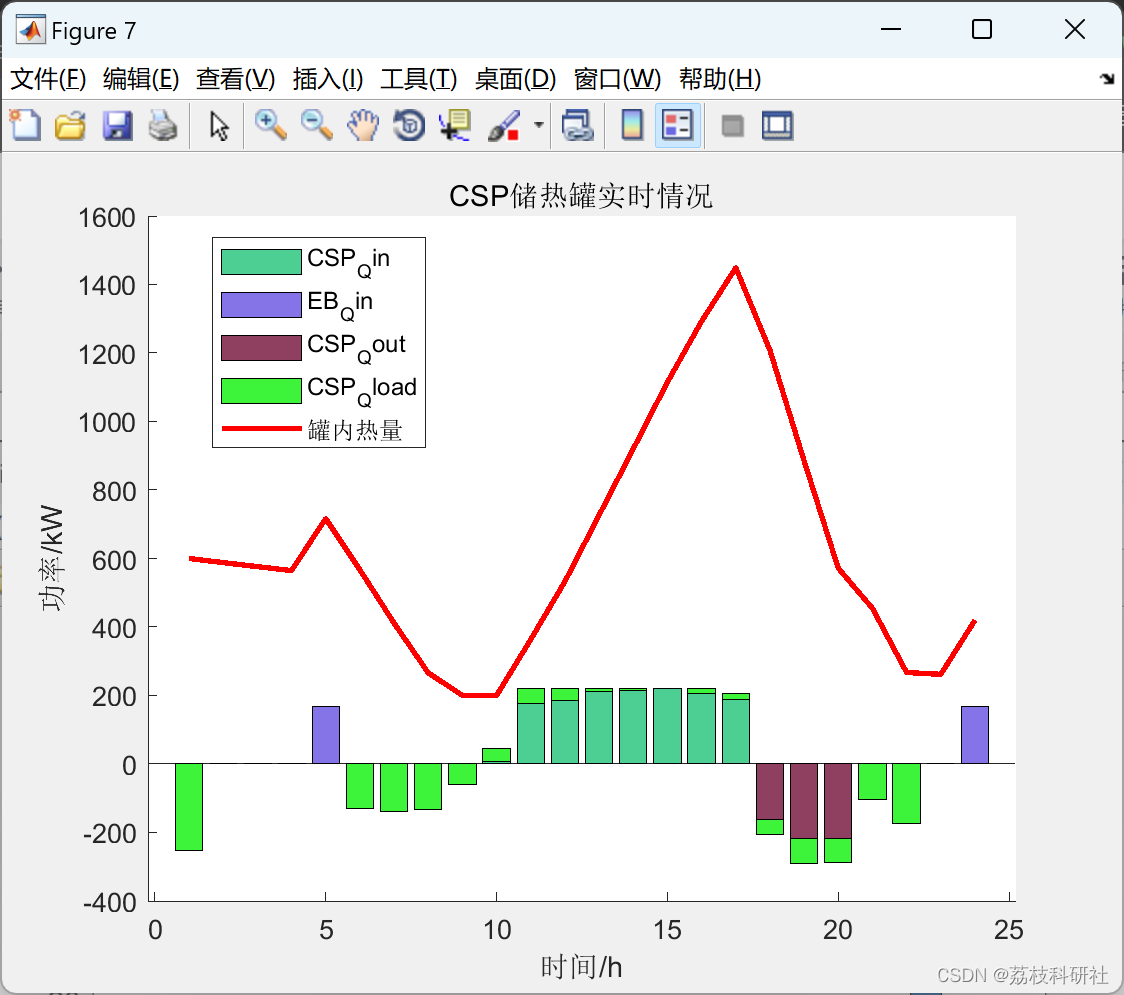
基于信息间隙决策理论的碳捕集电厂调度(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【C语言进阶:指针的进阶】回调函数
本章重点内容: 字符指针指针数组数组指针数组传参和指针传参函数指针函数指针数组指向函数指针数组的指针回调函数指针和数组面试题的解析什么是回调函数: 回调函数就是一个通过函数指针调用的函数。如果你把函数的指针(地址)作…...

C++模板的使用
在平时的工作和学习过程中,经常会用到泛型,这里对泛型和模板进行一下梳理,以便理解和使用。 模板关键字 template。为什么要使用模板? 假如设计一个两个参数的函数,用来求两个对象的乘积,在实践中我们可能需要定义n多个函数 int multipli…...

三天Golang快速入门—面向对象
面向对象Golang接口的定义go中类空接口空接口作为函数的参数切片实现空接口map的值实现空接口类型断言值接收者和指针接收者值接收者指针接收者接口嵌套Golang接口的定义 接口interface是一种抽象的类型。接口定义了一个对象的行为规范,只定义规范不实现࿰…...

开发手册——一、编程规约_6.并发处理
这篇文章主要梳理了在java的实际开发过程中的编程规范问题。本篇文章主要借鉴于《阿里巴巴java开发手册终极版》 下面我们一起来看一下吧。 1. 【强制】获取单例对象需要保证线程安全,其中的方法也要保证线程安全。 说明:资源驱动类、工具类、单例工厂…...

ACM---大一第三周周赛(Floyd算法+并查集算法学习周)
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...
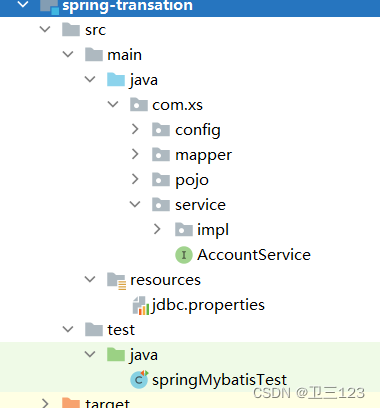
spring整合mybatis和Junit
该项目使用spring纯注解方式开发,用配置类取代spring的配置文件 一、导入依赖 整合Junit需要导入spring-test 整合mybatis需要导入spring-jdbc、mybatis-spring <dependencies><!-- https://mvnrepository.com/artifact/org.springframework/spring-cont…...

Spring Boot 3.0系列【7】核心特性篇之JSON
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot版本3.0.3 源码地址:https://gitee.com/pearl-organization/study-spring-boot3 文章目录 前言JSON什么是JSON常用JSON 库GsonFastJsonJacksonJackson 还是 FastjsonSpring Boot 中的 JSON1. 自动配置 Jackson2. @…...
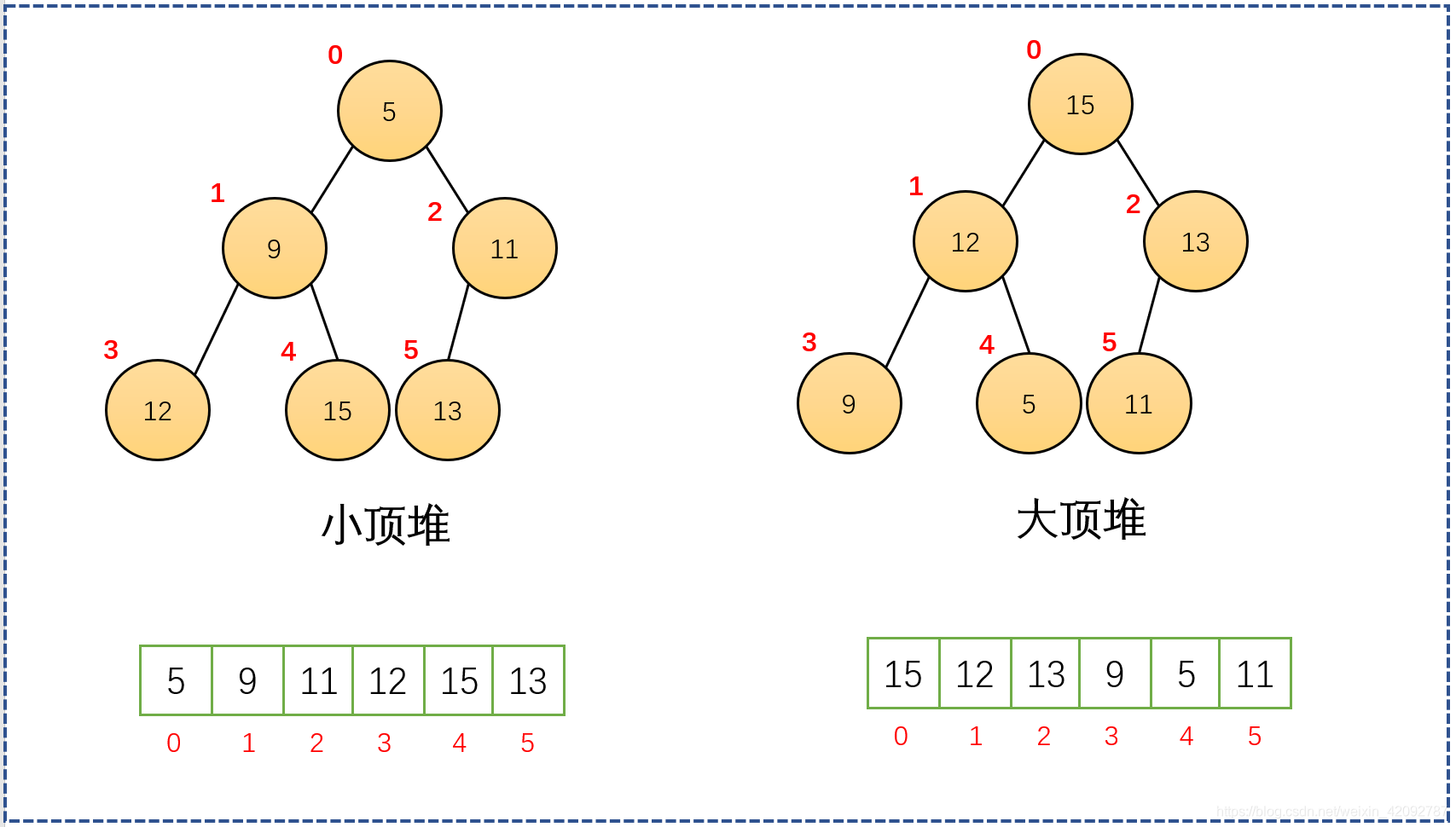
【数据结构初阶】二叉树顺序结构:堆的实现
前言 前边077带着大家学习了树与二叉树的相关概念,这篇文章我们来实现一个二叉树的顺序结构。 二叉树的顺序结构 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉…...
C/C++:动态内存管理
目录 一. C/C内存分布 二. C/C动态内存管理 2.1 C语言动态内存管理 2.2 C动态内存管理 2.2.1 new/delete操作符 2.2.2 operator new与operator delete函数 2.3 new/delete的实现原理 2.4 定位new(placement - new) 2.5 new/delete和malloc/free的…...
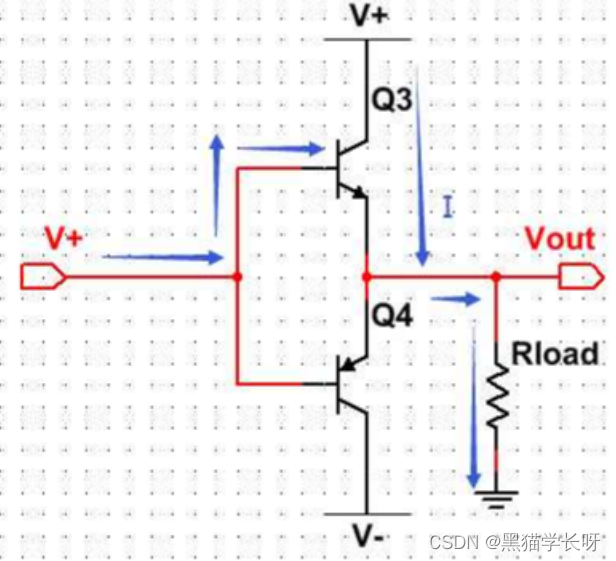
黑猫带你学eMMC协议第28篇:eMMC的开漏和推挽模式(push-pull open drain)
本文依据eMMC JEDEC5.1及个人工作经验整理而成,如有错误请留言。 文章为个人辛苦整理,付费内容,已加入原创侵权保护,禁止私自转载。 文章所在专栏:《黑猫带你学:eMMC协议详解》 1 什么是开漏和推挽 1.1 推挽电路是什么 关于推挽和开漏电路,更多介绍详见我的另一篇文章…...
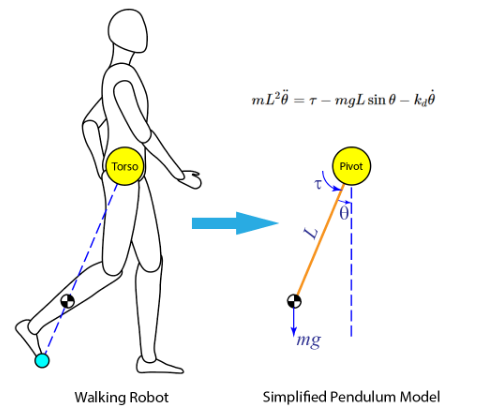
simulink PID控制
系列文章目录 文章目录系列文章目录前言一、非线性系统线性化原理二、反馈控制开环控制反馈or闭环控制PID ControllerPID微调案例总结前言 将非线性系统近似线性化PIDblock与微调 提示:以下是本篇文章正文内容,下面案例可供参考 一、非线性系统线性化 …...

如何在for循环内执行异步操作
var定义的i是全局的,每次遍历都会覆盖,最后i的值为10,所以输出10次10 for (var i 0; i < 10; i) {setTimeout(function () {console.log(i) // 输出10遍10}, 1000 i * 100)}setTimeOut 第三个函数 for (var i 0; i < 10; i) {setT…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
