【数据结构初阶】二叉树顺序结构:堆的实现
前言
前边077带着大家学习了树与二叉树的相关概念,这篇文章我们来实现一个二叉树的顺序结构。
二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
与前边的栈类似,数据结构中的堆与地址空间的堆是完全不同的,是两个学科中的名词。

堆的概念及结构
堆的性质:堆中某个节点的值总是不大于或不小于其父节点的值;堆总是一棵完全二叉树。
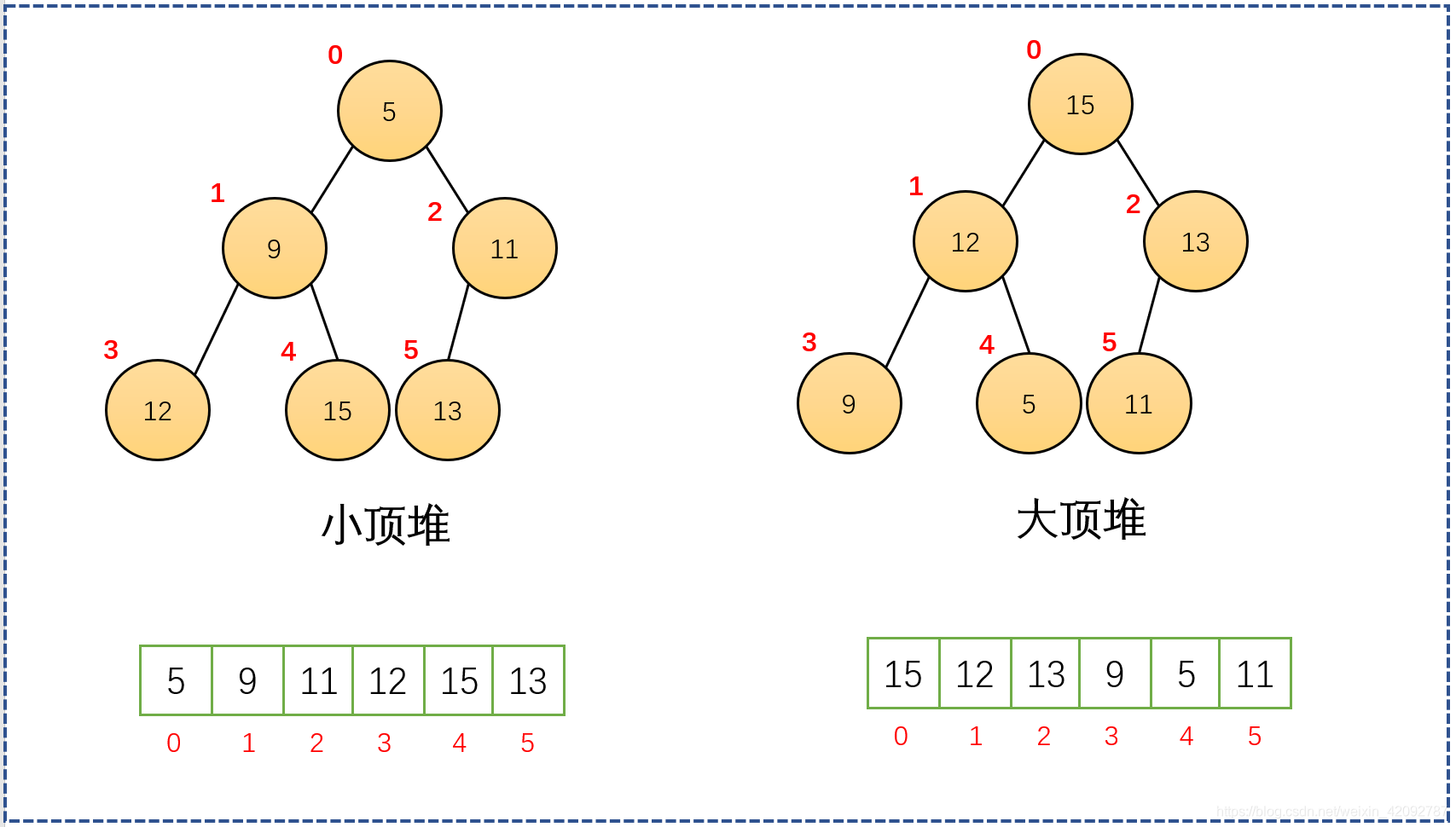
堆的实现
堆的接口实现
1.堆的结构
typedef int hpDataType;
typedef struct heap
{hpDataType* a;int size;int capacity;
}hp;void hpInit(hp* ph)
{assert(ph);ph->a = NULL;ph->capacity = ph->size = 0;
}3.销毁顺序表
void hpDestory(hp* ph)
{assert(ph);free(ph->a);ph->a = NULL;ph->capacity = ph->size = 0;
}4.向上调整
void adjustUp(hpDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){int tmp = a[child];a[child] = a[parent];a[parent] = tmp;child = parent;parent = (child - 1) / 2;}else{break;}}
}使用向上调整算法可以随意插入数据,并且还不改变堆,还为一个小堆或者大堆,我这里实现的是一个大堆。
void hpPush(hp* ph, hpDataType x)
{assert(ph);if (ph->size == ph->capacity){hpDataType newCapacity = ph->capacity == 0 ? 4 : ph->capacity * 2;hpDataType* tmp = (hpDataType*)realloc(ph->a, sizeof(hpDataType)*newCapacity);if (tmp == NULL){perror("realloc fail/n");exit(-1);}ph->a = tmp;ph->capacity = newCapacity;}ph->a[ph->size] = x;ph->size++;adjustUp(ph->a, ph->size - 1);
}在堆中插入数据的前提是不改变堆的性质,使其还是一个堆,所以我们可以在最后一个位置处插入数据,再调用向上调整函数来实现插入,当然与顺序表相同的是,当容量不够时我们要进行扩容操作。
6.向下调整算法
void adjustDown(hpDataType* a, int size, int parent)
{int child = parent * 2 + 1;//调整到没有孩子结点while (child < size){if (child + 1 < size && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){swap(&a[parent], & a[child]);parent = child;child = parent * 2 + 1;}else{break;} }
}我们使用向下调整函数也可以实现大堆和小堆,当某一节点不存在孩子结点时,向下调整结束,由于一个父节点存在左子树和右子树,所以我们在调整时,应该判断左右子树数据的大小并且判断右子树是否存在,来决定child的位置,再比较与父节点的位置来交换父节点与孩子结点。
7.堆的删除
void hpPop(hp* ph)
{assert(ph);assert(!hpEmpty(ph));swap(&ph->a[ph->size - 1], &ph->a[0]);ph->size--;adjustDown(ph->a, ph->size, 0);
}堆中数据的删除实际上指的是将堆顶数据进行删除,我们要进行的操作是将堆中最后一个数与堆顶元素互换,然后将堆的数据个数减一,这样就删除了堆顶元素,但是此时可能改变了堆的结构,我们再使用向下调整算法,调整根节点就能恢复了。
8.判空
bool hpEmpty(hp* ph)
{assert(ph);return ph->size == 0;
}9.取堆顶数据
hpDataType hpTop(hp* ph)
{assert(ph);assert(!hpEmpty(ph));return ph->a[0];
}10.打印堆中数据
void hpPrint(hp* hp)
{for (int i = 0; i < hp->size; ++i){printf("%d ", hp->a[i]);}printf("\n");
}源码
heap.h
#include<stdlib.h>
#include<stdbool.h>
#include<time.h>
typedef int hpDataType;
typedef struct heap
{hpDataType* a;int size;int capacity;
}hp;
void adjustUp(hpDataType* a, int child);
void adjustDown(hpDataType* a, int size, int child);void swap(int* px, int* py);
void hpInit(hp* ph);
void hpDestory(hp* ph);
void hpPush(hp* ph, hpDataType x);
void hpPop(hp* ph);
bool hpEmpty(hp* ph);
void hpPrint(hp* ph);
hpDataType hpTop(hp* ph);heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"heap.h"
void swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}
void adjustUp(hpDataType* a, int child)
{int parent = (child - 1) / 2;//调整到孩子结点就是根节点结束while (child > 0){if (a[child] > a[parent]){int tmp = a[child];a[child] = a[parent];a[parent] = tmp;child = parent;parent = (child - 1) / 2;}else{break;}}
}
void adjustDown(hpDataType* a, int size, int parent)
{int child = parent * 2 + 1;//调整到没有孩子结点while (child < size){if (child + 1 < size && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){swap(&a[parent], & a[child]);parent = child;child = parent * 2 + 1;}else{break;} }
}
void hpInit(hp* ph)
{assert(ph);ph->a = NULL;ph->capacity = ph->size = 0;
}
void hpDestory(hp* ph)
{assert(ph);free(ph->a);ph->a = NULL;ph->capacity = ph->size = 0;
}void hpPush(hp* ph, hpDataType x)
{assert(ph);if (ph->size == ph->capacity){hpDataType newCapacity = ph->capacity == 0 ? 4 : ph->capacity * 2;hpDataType* tmp = (hpDataType*)realloc(ph->a, sizeof(hpDataType)*newCapacity);if (tmp == NULL){perror("realloc fail/n");exit(-1);}ph->a = tmp;ph->capacity = newCapacity;}ph->a[ph->size] = x;ph->size++;adjustUp(ph->a, ph->size - 1);
}
void hpPop(hp* ph)
{assert(ph);assert(!hpEmpty(ph));swap(&ph->a[ph->size - 1], &ph->a[0]);ph->size--;adjustDown(ph->a, ph->size, 0);}
bool hpEmpty(hp* ph)
{assert(ph);return ph->size == 0;
}
void hpPrint(hp* hp)
{for (int i = 0; i < hp->size; ++i){printf("%d ", hp->a[i]);}printf("\n");
}
hpDataType hpTop(hp* ph)
{assert(ph);assert(!hpEmpty(ph));return ph->a[0];
}
test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"heap.h"void test()
{hp h;hpInit(&h);int a[] = { 70, 56, 30, 25, 15, 10, 1 };for (int i = 0; i < sizeof(a) / sizeof(a[0]); ++i){hpPush(&h, a[i]);}hpPrint(&h);hpDestory(&h);
}
int main()
{test();//testTopk();return;
}相关文章:

【数据结构初阶】二叉树顺序结构:堆的实现
前言 前边077带着大家学习了树与二叉树的相关概念,这篇文章我们来实现一个二叉树的顺序结构。 二叉树的顺序结构 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉…...
C/C++:动态内存管理
目录 一. C/C内存分布 二. C/C动态内存管理 2.1 C语言动态内存管理 2.2 C动态内存管理 2.2.1 new/delete操作符 2.2.2 operator new与operator delete函数 2.3 new/delete的实现原理 2.4 定位new(placement - new) 2.5 new/delete和malloc/free的…...
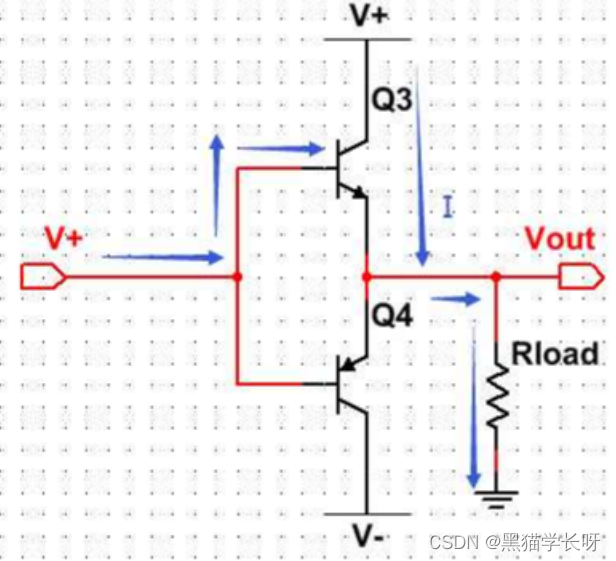
黑猫带你学eMMC协议第28篇:eMMC的开漏和推挽模式(push-pull open drain)
本文依据eMMC JEDEC5.1及个人工作经验整理而成,如有错误请留言。 文章为个人辛苦整理,付费内容,已加入原创侵权保护,禁止私自转载。 文章所在专栏:《黑猫带你学:eMMC协议详解》 1 什么是开漏和推挽 1.1 推挽电路是什么 关于推挽和开漏电路,更多介绍详见我的另一篇文章…...
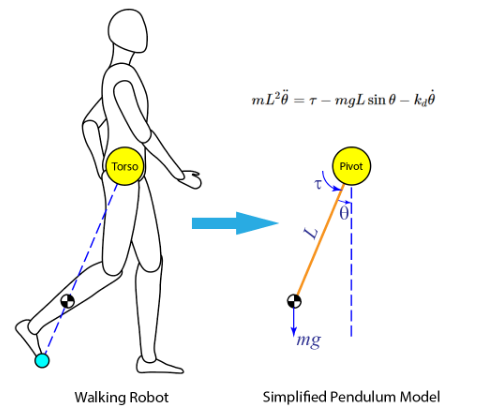
simulink PID控制
系列文章目录 文章目录系列文章目录前言一、非线性系统线性化原理二、反馈控制开环控制反馈or闭环控制PID ControllerPID微调案例总结前言 将非线性系统近似线性化PIDblock与微调 提示:以下是本篇文章正文内容,下面案例可供参考 一、非线性系统线性化 …...

如何在for循环内执行异步操作
var定义的i是全局的,每次遍历都会覆盖,最后i的值为10,所以输出10次10 for (var i 0; i < 10; i) {setTimeout(function () {console.log(i) // 输出10遍10}, 1000 i * 100)}setTimeOut 第三个函数 for (var i 0; i < 10; i) {setT…...
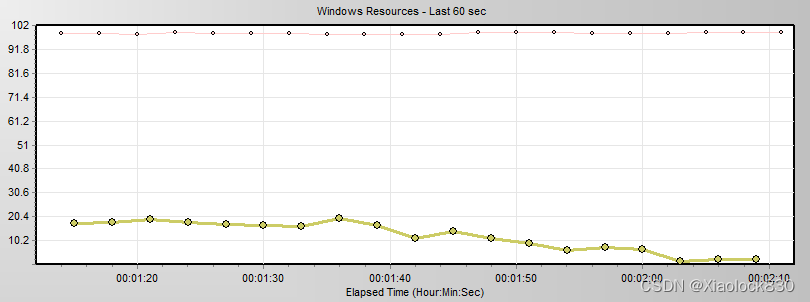
性能测试——LoadRunner: Controller的使用
Controller Controller是用来创建测试环境,执行在VUG中编写的测试脚本 可以直接点击Controller的快捷方式打开,也可以在VUG中打开 这里将虚拟用户数设置为3,比较适合自己的电脑性能 整个controller分为下面几个模块 这里先设置左下角的目标计划 设置初始化:双击…...
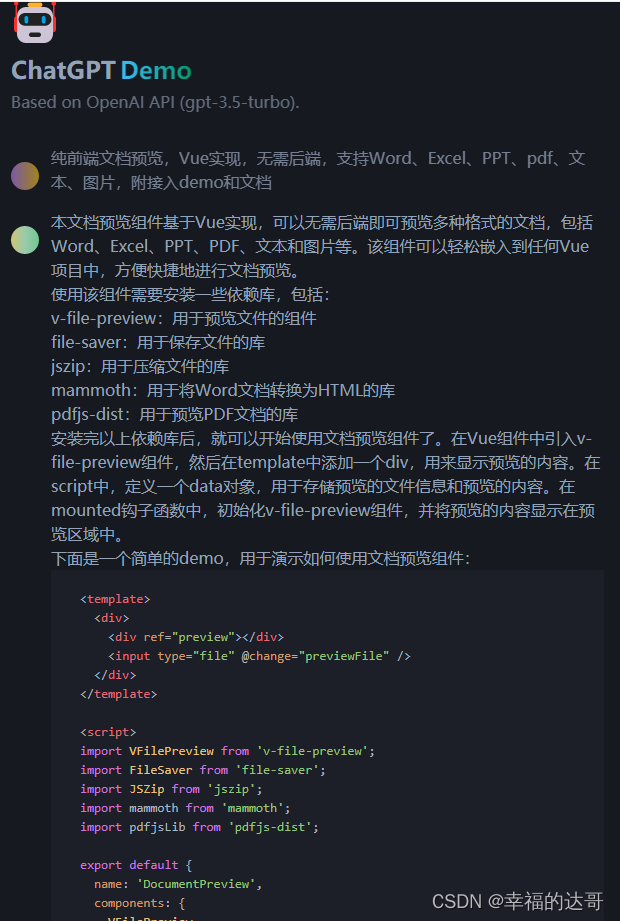
ChatGPT解答:纯前端文档预览,Vue实现,无需后端,支持Word、Excel、PPT、pdf、文本、图片,附接入demo和文档
ChatGPT解答:纯前端文档预览,Vue实现,无需后端,支持Word、Excel、PPT、pdf、文本、图片,附接入demo和文档 ChatGPTDemo Based on OpenAI API (gpt-3.5-turbo). 纯前端文档预览,Vue实现,无需后…...

刷题记录:牛客NC13950 Alliances 到树上联通点集的最短距离
传送门:牛客 题目描述: 题目较长,此处省略 输入: 7 1 2 1 3 2 4 2 5 3 6 3 7 2 2 6 7 1 4 3 5 1 2 1 1 1 5 2 1 2 输出: 2 1 1一道比较复杂的树题.需要一些复杂的讨论以及LCA知识 对于LCA,可以使用树链剖分进行解决 然后我们看一下题目,我们会发现有这样一个简单的结论,那就…...
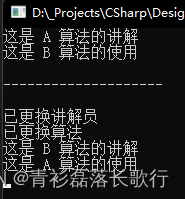
行为型模式 - 状态模式State
学习而来,代码是自己敲的。也有些自己的理解在里边,有问题希望大家指出。 个人理解:感觉像桥接模式 代理模式。不知道这么想对不对,还希望笔记在放出后,有大佬彻底了解了给我解解惑。 策略模式的定义与特点 策略&…...

电视剧《狂飙》太过诡异,主演各个悄无声息,龙套演员却身价倍增
说起电视剧《狂飙》,相信很多人都有过观看,这部以反腐为题材的大剧,尺度之大近年来绝无仅有。不过观众在被剧情震撼的同时,也发现了一些诡异的事情,比如说主角和配角的反差,让人感觉很不适应。 在电视剧《狂…...

【微信小程序】-- 案例 - 本地生活(二十)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

LeetCode 每日一题 2023/2/27-2023/3/5
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录2/27 1144. 递减元素使数组呈锯齿状2/28 2363. 合并相似的物品3/1 2373. 矩阵中的局部最大值3/2 面试题 05.02. 二进制数转字符串3/3 1487. 保证文件名唯一3/4 982. 按位与为…...

SpringMVC中JSON数据的设置、RestFul风格
Java知识点总结:想看的可以从这里进入 目录3.4、JSON数据3.4.1、前端使用3.4.2、后端使用1、Jackson2、fastjson3.5、RestFul风格3.5.1、简介3.5.2、使用3.4、JSON数据 3.4.1、前端使用 前端在JavaScript中有封装的JSON对象,可以直接用来操作JSON数据。…...
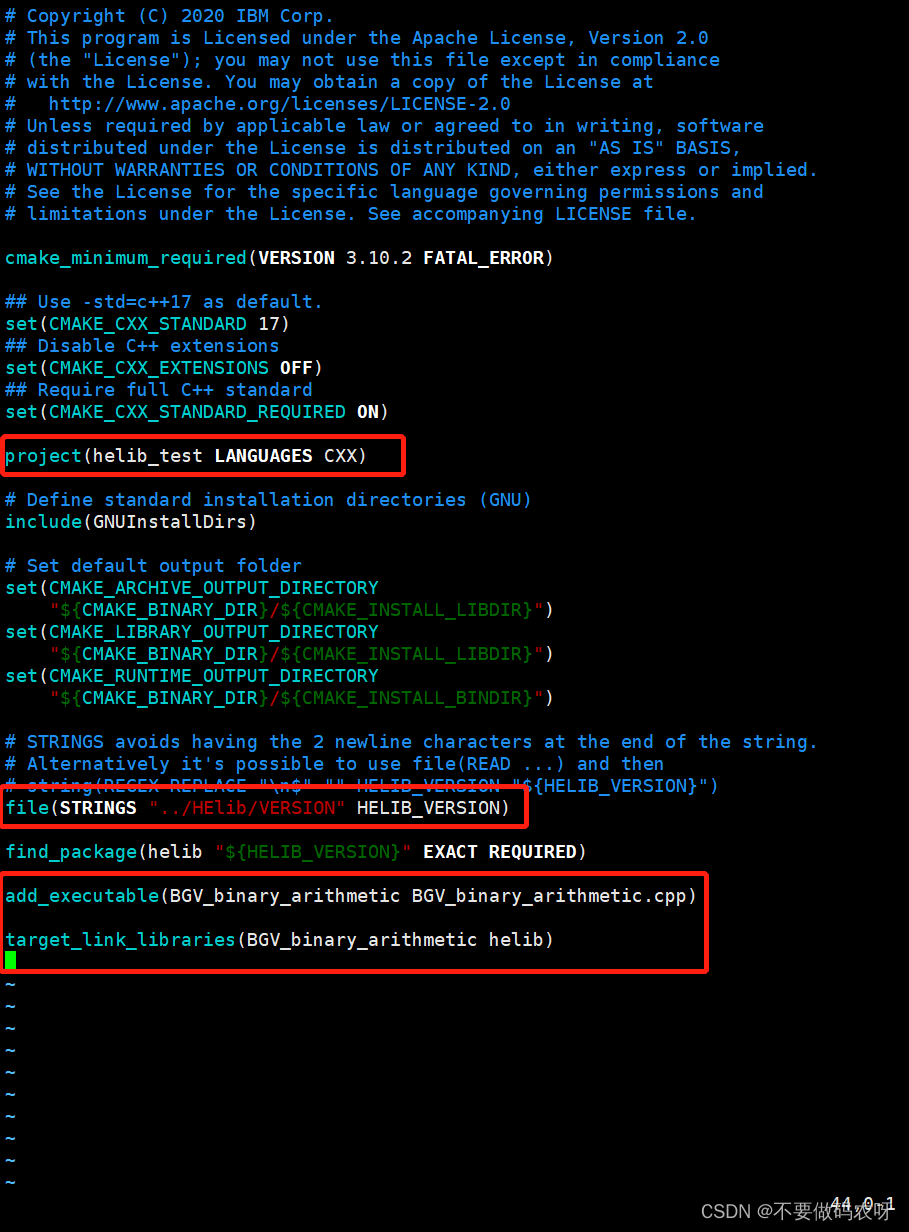
Clion连接Docker,使用HElib库
文章目录需求Clion连接服务器内的DockerDockerCLionDocker内配置HElib库参考需求 HElib库是用C编写的同态加密开源库,一般在Linux下使用为了不混淆生产环境,使用Docker搭建HElib运行环境本地在Windows下开发,使用的IDE为Clion,本…...

go网络编程-websocket
1. WebSocket编程 文章目录1. WebSocket编程1.1.1. webSocket是什么1.1.2. 举个聊天室的小例子server.go文件代码hub.go文件代码data.go文件代码local.html文件代码1.1.1. webSocket是什么 WebSocket是一种在单个TCP连接上进行全双工通信的协议 WebSocket使得客户端和服务器之…...
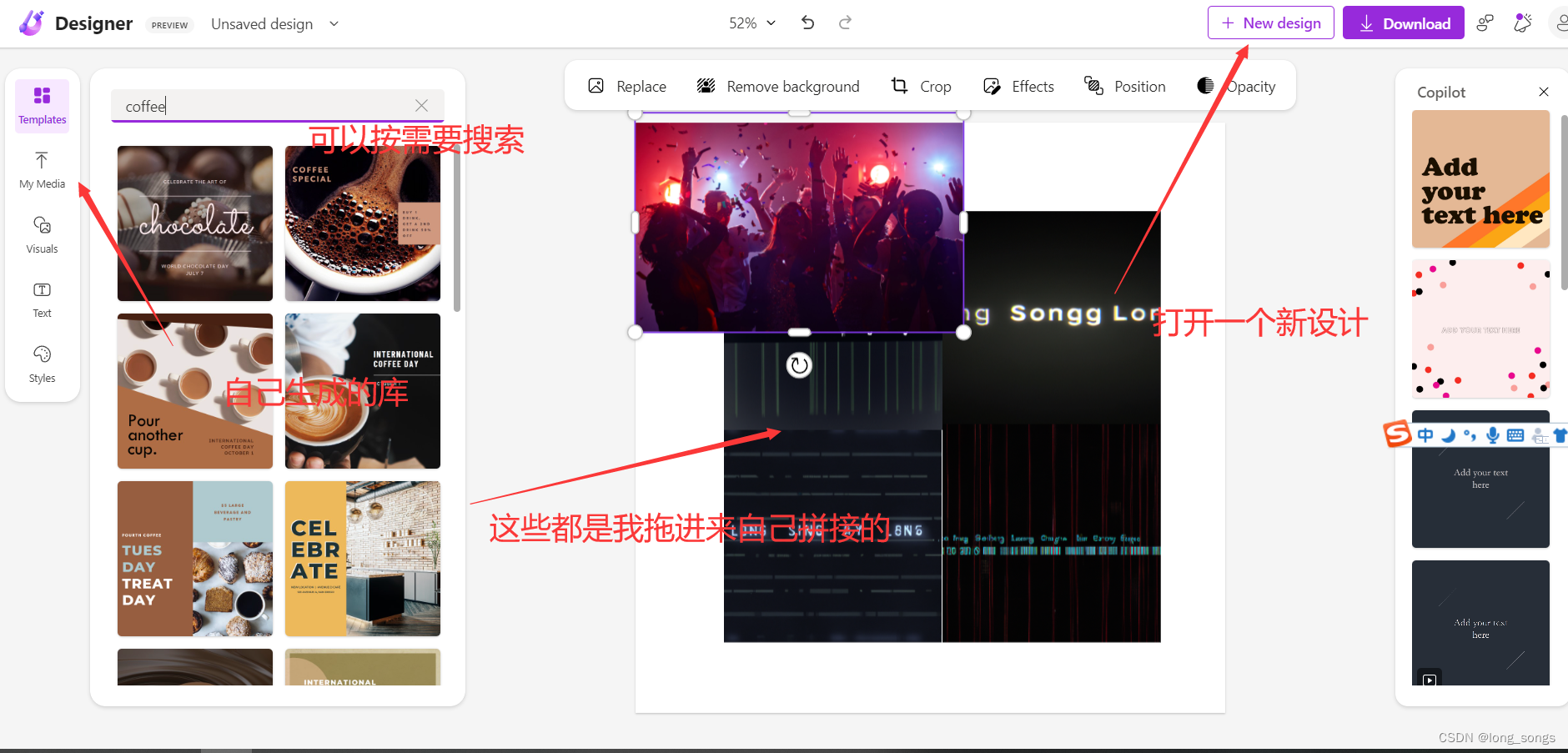
Microsoft designer 使用教程
继各种ai绘图软件诞生之后 dell 2 playground.... 微软自己研发的重量级产品 Microsoft designer 上线了 Microsoft Designer 是微软公司推出的一款设计工具,主要用于快速创建Web和移动应用程序的原型设计。它提供了一系列的工具和模板,可以帮助用户…...

《Docker系列》Docker容器修改配置文件后,重启失败,如何修改配置并启动容器?
Docker容器修改配置文件后,重启失败,如何修改配置并启动容器? docker部署的MySQL容器,修改了my.cnf配置文件,重启的时候导致无法启动 通过查日志发现,配置文件中的binlog-db-dbhw写错了,应该是…...

遇到多个构造器参数时要考虑使用构建器
静态工厂和构造器有个共同的局限性:他们都不能很好地扩展到大量的可选参数。比如用一个类表示包装食品外面显示的营养成分标签(包括必选域和可选域)。 重叠构造器 对于这样的类一般习惯采用重叠构造器(telescoping constructor&…...
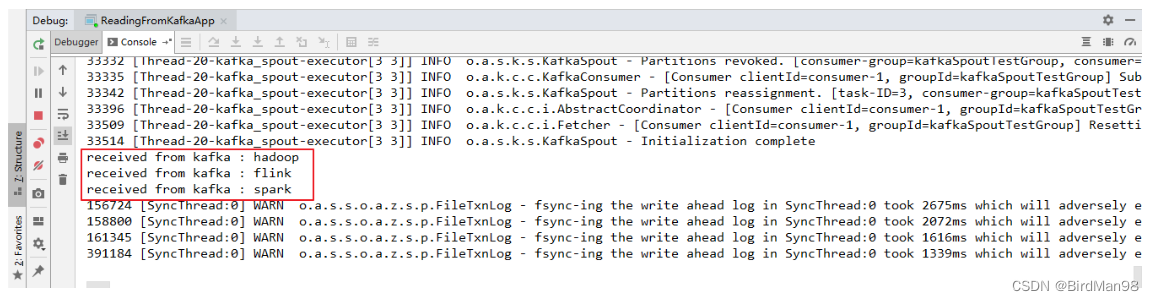
【Storm】【五】Storm集成Kafka
Storm集成Kafka 一、整合说明二、写入数据到Kafka三、从Kafka中读取数据一、整合说明 Storm 官方对 Kafka 的整合分为两个版本,官方说明文档分别如下: Storm Kafka Integration : 主要是针对 0.8.x 版本的 Kafka 提供整合支持;Storm Kafka …...

GVRP-LNP-VCMP讲解
目录 GVRP讲解 动态创建Vlan并将端口加入Vlan GVRP消息类型 GVRP工作原理 LNP讲解 动态修改接口链路类型 VCMP讲解 动态创建Vlan 相关概念 Vlan同步 VCMP与GVRP的区别 GVRP讲解 动态创建Vlan并将端口加入Vlan GVRP(GARR Vlan Registration Protocol…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
