刷题记录:牛客NC13950 Alliances 到树上联通点集的最短距离
传送门:牛客
题目描述:
题目较长,此处省略
输入:
7
1 2
1 3
2 4
2 5
3 6
3 7
2
2 6 7
1 4
3
5 1 2
1 1 1
5 2 1 2
输出:
2
1
1
一道比较复杂的树题.需要一些复杂的讨论以及LCA知识
对于LCA,可以使用树链剖分进行解决
然后我们看一下题目,我们会发现有这样一个简单的结论,那就是我们的两个点<u,v>被占领的时候,那么他们的祖先LCA(u,v)LCA(u,v)LCA(u,v)也必然是被占领的.(这个很好理解,因为我们的,uv肯定是穿过他们的祖先节点的).所以我们可以预处理出每一个帮派的LCALCALCA
同样的对于我们后来的联盟,我们可以求出这些联盟共同的LCALCALCA
那么对于一个首都vvv来说,此时的vvv有以下几种情况:
- 当vvv不是我们LCALCALCA的子节点.因为我们的被占领的地方肯定是一个联通图,所以此时我们的最短距离显然是vvv到第一个联通图上的一点,那么此时的那一个点就是我们的LCA(可以自己画图理解理解)
- 我们的vvv是我们的LCALCALCA的子节点.
此时我们可以预处理出所有节点的dfsdfsdfs序,那么对于此时我们的vvv来说,又有这几种情况:.
1.比v dfsdfsdfs序小的最近节点的是v的父亲,此时显然最短距离就是这个点与v的距离,注意肯定是一个联通图,而我们的v处于这个位置,所以在v的节点中不可能存在一个点是被占领的
2.比v dfsdfsdfs序小的最近节点是vvv的兄弟,设为u1,此时我们需要看一下dfsdfsdfs大的最近节点(设为u2)的情况,根据dfs遍历的性质,dfs序大的节点不可能是v的父亲了,此时必然是v的兄弟.所以此时我们的LCA(u1,v)和LCA(u2,v)的一个点到v的距离必然有一个是最短的.这里感觉很难说明清楚,因为用到了dfs遍历的性质,感觉使用到了dfs遍历中的夹逼性质,但是通过画图还是很好理解的
对于树上两点之间距离,可以使用到根节点的距离来进行解决
dis[u][v]=dist[u]+dist[v]−2∗dist[LCA(u,v)]dis[u][v]=dist[u]+dist[v]-2*dist[LCA(u,v)]dis[u][v]=dist[u]+dist[v]−2∗dist[LCA(u,v)]
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int fa[maxn],Size[maxn],max_son[maxn],dep[maxn];
vector<int>edge[maxn];
void dfs1(int u,int per_u) {Size[u]=1;for(int i=0;i<edge[u].size();i++) {int v=edge[u][i];if(v==per_u) continue;dep[v]=dep[u]+1;dfs1(v,u);fa[v]=u;Size[u]+=Size[v];if(Size[v]>Size[max_son[u]]) {max_son[u]=v;}}
}
int top[maxn];
void dfs2(int u,int t) {top[u]=t;if(!max_son[u]) return ;dfs2(max_son[u],t);for(int i=0;i<edge[u].size();i++) {int v=edge[u][i];if(v==fa[u]||v==max_son[u]) continue;dfs2(v,v);}
}
int LCA(int u,int v) {while(top[u]!=top[v]) {if(dep[top[u]]<dep[top[v]]) swap(u,v);u=fa[top[u]];}if(dep[u]>dep[v]) swap(u,v);return u;
}/*============================================================*/int n,k;int c[maxn],lc[maxn],t[maxn];//lc记录每一个帮派管的点的LCA
vector<int>g[maxn];//记录每一个帮派管的点的dfs序
int dfsn[maxn],dfscnt=0,pos[maxn];//记录dfs序
void dfs(int u,int per_u) {dfsn[u]=++dfscnt;pos[dfscnt]=u;for(int i=0;i<edge[u].size();i++) {int v=edge[u][i];if(v==per_u) continue;dfs(v,u);}
}
int get_dist(int u,int v) {return dep[u]+dep[v]-2*dep[LCA(u,v)];
}/*============================================================*/int main() {n=read();for(int i=1;i<=n-1;i++) {int u=read(),v=read();edge[u].push_back(v);edge[v].push_back(u);}dfs1(1,0);dfs2(1,1);dfs(1,1);int k=read();for(int i=1;i<=k;i++) {int num=read();for(int j=1;j<=num;j++) {c[j]=read();if(j==1) lc[i]=c[j];else lc[i]=LCA(lc[i],c[j]);g[i].push_back(dfsn[c[j]]);}sort(g[i].begin(),g[i].end());}int q=read();for(int i=1;i<=q;i++) {int v=read(),num=read();for(int j=1;j<=num;j++) t[j]=read();int lca=lc[t[1]];for(int j=2;j<=num;j++) lca=LCA(lca,lc[t[j]]);if(LCA(lca,v)!=lca) {printf("%d\n",get_dist(lca,v));continue;}int ans=int_INF;for(int j=1;j<=num;j++) {int tmp=t[j];auto p=lower_bound(g[tmp].begin(),g[tmp].end(),dfsn[v]);if(p!=g[tmp].end()) { ans=min(ans,get_dist(v,LCA(v,pos[*p])));}if(p!=g[tmp].begin()) {ans=min(ans,get_dist(v,LCA(v,pos[*prev(p)])));}}cout<<ans<<endl;}return 0;
}
相关文章:

刷题记录:牛客NC13950 Alliances 到树上联通点集的最短距离
传送门:牛客 题目描述: 题目较长,此处省略 输入: 7 1 2 1 3 2 4 2 5 3 6 3 7 2 2 6 7 1 4 3 5 1 2 1 1 1 5 2 1 2 输出: 2 1 1一道比较复杂的树题.需要一些复杂的讨论以及LCA知识 对于LCA,可以使用树链剖分进行解决 然后我们看一下题目,我们会发现有这样一个简单的结论,那就…...
行为型模式 - 状态模式State
学习而来,代码是自己敲的。也有些自己的理解在里边,有问题希望大家指出。 个人理解:感觉像桥接模式 代理模式。不知道这么想对不对,还希望笔记在放出后,有大佬彻底了解了给我解解惑。 策略模式的定义与特点 策略&…...

电视剧《狂飙》太过诡异,主演各个悄无声息,龙套演员却身价倍增
说起电视剧《狂飙》,相信很多人都有过观看,这部以反腐为题材的大剧,尺度之大近年来绝无仅有。不过观众在被剧情震撼的同时,也发现了一些诡异的事情,比如说主角和配角的反差,让人感觉很不适应。 在电视剧《狂…...

【微信小程序】-- 案例 - 本地生活(二十)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

LeetCode 每日一题 2023/2/27-2023/3/5
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录2/27 1144. 递减元素使数组呈锯齿状2/28 2363. 合并相似的物品3/1 2373. 矩阵中的局部最大值3/2 面试题 05.02. 二进制数转字符串3/3 1487. 保证文件名唯一3/4 982. 按位与为…...

SpringMVC中JSON数据的设置、RestFul风格
Java知识点总结:想看的可以从这里进入 目录3.4、JSON数据3.4.1、前端使用3.4.2、后端使用1、Jackson2、fastjson3.5、RestFul风格3.5.1、简介3.5.2、使用3.4、JSON数据 3.4.1、前端使用 前端在JavaScript中有封装的JSON对象,可以直接用来操作JSON数据。…...
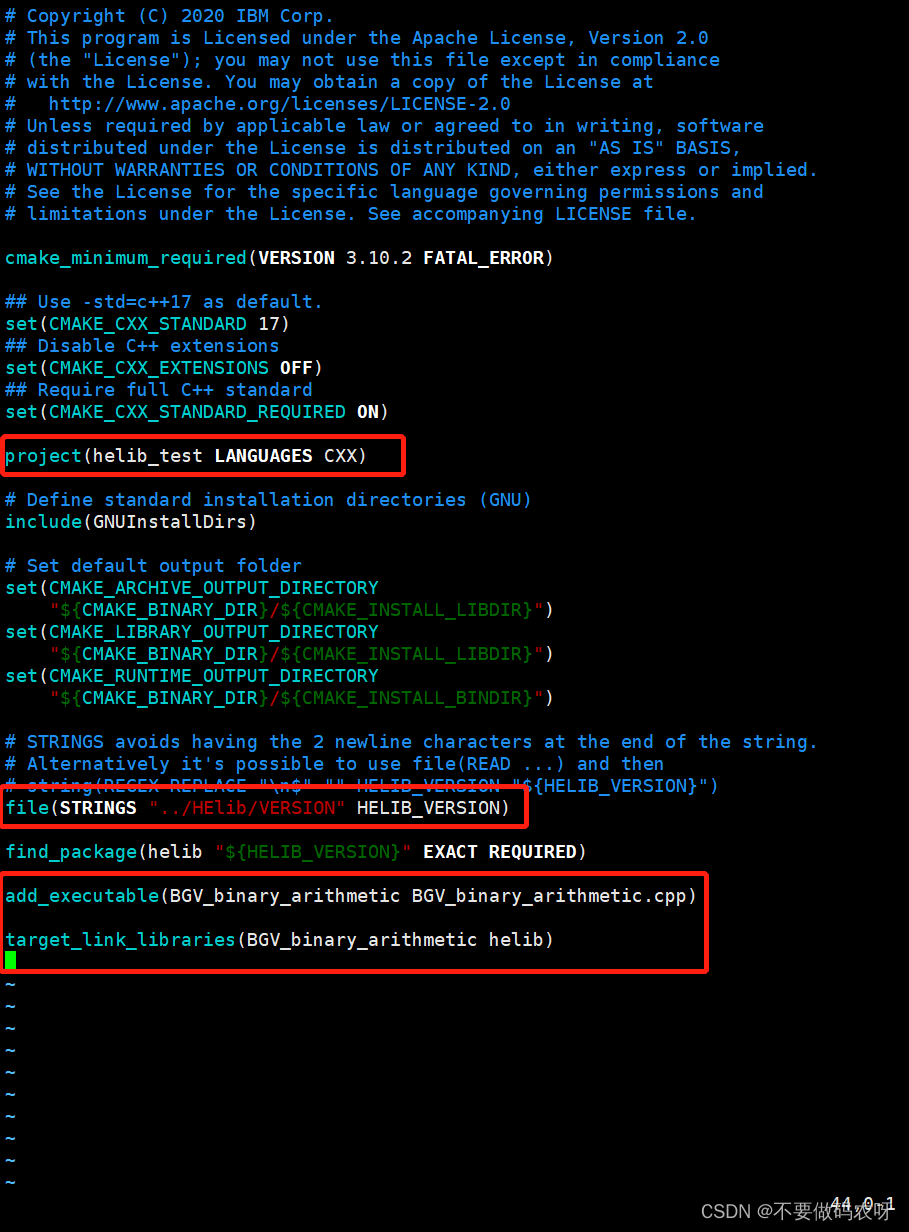
Clion连接Docker,使用HElib库
文章目录需求Clion连接服务器内的DockerDockerCLionDocker内配置HElib库参考需求 HElib库是用C编写的同态加密开源库,一般在Linux下使用为了不混淆生产环境,使用Docker搭建HElib运行环境本地在Windows下开发,使用的IDE为Clion,本…...

go网络编程-websocket
1. WebSocket编程 文章目录1. WebSocket编程1.1.1. webSocket是什么1.1.2. 举个聊天室的小例子server.go文件代码hub.go文件代码data.go文件代码local.html文件代码1.1.1. webSocket是什么 WebSocket是一种在单个TCP连接上进行全双工通信的协议 WebSocket使得客户端和服务器之…...
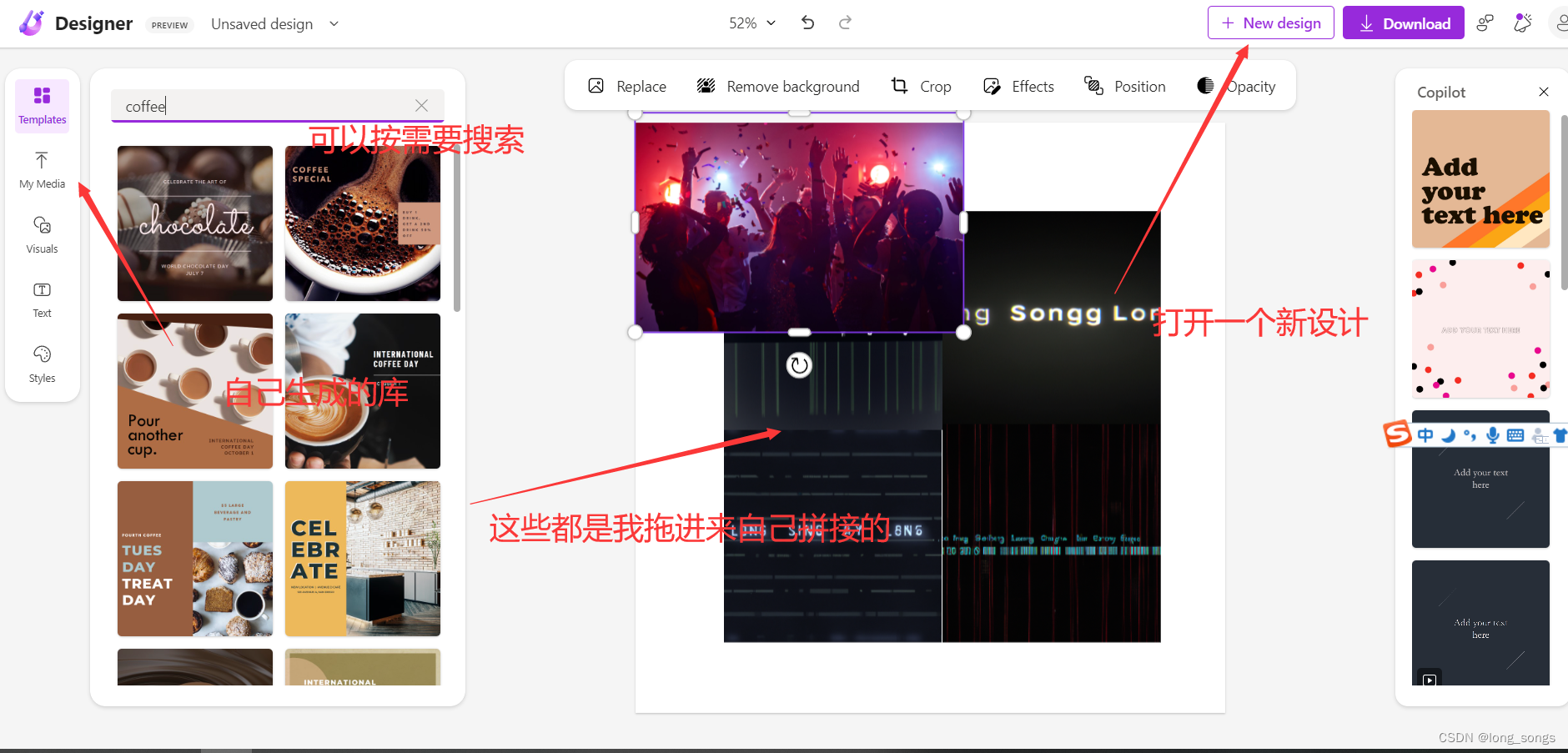
Microsoft designer 使用教程
继各种ai绘图软件诞生之后 dell 2 playground.... 微软自己研发的重量级产品 Microsoft designer 上线了 Microsoft Designer 是微软公司推出的一款设计工具,主要用于快速创建Web和移动应用程序的原型设计。它提供了一系列的工具和模板,可以帮助用户…...

《Docker系列》Docker容器修改配置文件后,重启失败,如何修改配置并启动容器?
Docker容器修改配置文件后,重启失败,如何修改配置并启动容器? docker部署的MySQL容器,修改了my.cnf配置文件,重启的时候导致无法启动 通过查日志发现,配置文件中的binlog-db-dbhw写错了,应该是…...

遇到多个构造器参数时要考虑使用构建器
静态工厂和构造器有个共同的局限性:他们都不能很好地扩展到大量的可选参数。比如用一个类表示包装食品外面显示的营养成分标签(包括必选域和可选域)。 重叠构造器 对于这样的类一般习惯采用重叠构造器(telescoping constructor&…...
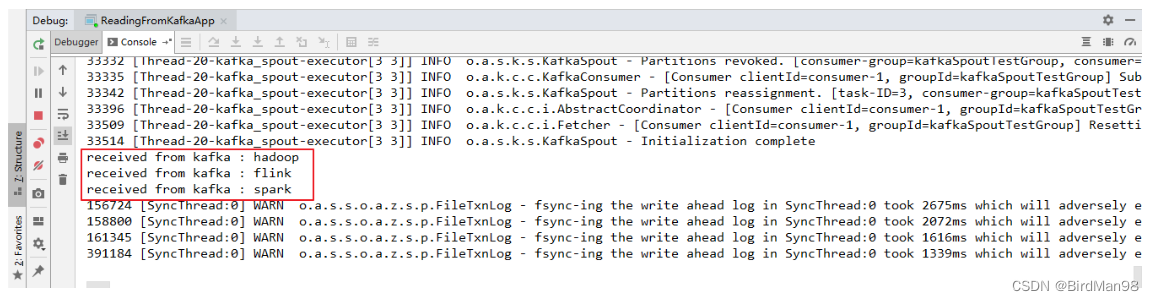
【Storm】【五】Storm集成Kafka
Storm集成Kafka 一、整合说明二、写入数据到Kafka三、从Kafka中读取数据一、整合说明 Storm 官方对 Kafka 的整合分为两个版本,官方说明文档分别如下: Storm Kafka Integration : 主要是针对 0.8.x 版本的 Kafka 提供整合支持;Storm Kafka …...

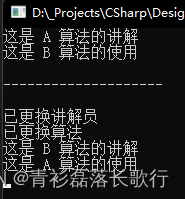
GVRP-LNP-VCMP讲解
目录 GVRP讲解 动态创建Vlan并将端口加入Vlan GVRP消息类型 GVRP工作原理 LNP讲解 动态修改接口链路类型 VCMP讲解 动态创建Vlan 相关概念 Vlan同步 VCMP与GVRP的区别 GVRP讲解 动态创建Vlan并将端口加入Vlan GVRP(GARR Vlan Registration Protocol…...

28个精品Python爬虫实战项目
先来说说Python的优势!然后给大家看下这28个实战项目的实用性!Python跟其他语言相比,有以下优点:1. 简单Python是所有编程语言里面,代码量最低,非常易于读写,遇到问题时,程序员可以把…...

相信人还是相信ChatGPT,龙测首席AI专家给出了意料之外的答案
最近,关于ChatGPT的话题太火了!各大社交软件都是他的消息!从去年12月份ChatGPT横空出世,再到近期百度文心一言、复旦Moss的陆续宣布,点燃了全球对AIGC(内容人工智能自动生成)领域的热情…...

安卓逆向_5 --- jeb 和 AndroidStudio 动态调试 smali
Jeb 工具的使用 :https://www.52pojie.cn/forum.php?modviewthread&tid742250:https://zhuanlan.zhihu.com/p/302856081动态调试 smali 有两种方法: Jeb 调试AndroidStudio smalidea 插件动态调试。1、Jeb 动态调试 smali JEB是一个…...

docker-容器命令
1.新建启动 docker run options image command [arg..] options: --name"容器新名字" -d:后台运行程序 -it:交互式运行 -P: 随机端口 -p: 指定端口 docker run -it ubuntu /bin/bash docker run -it ubuntu:v1 /bin/bash docker run -it 1c352…...
Spring——是什么?作用?内容?用到的设计模式?
目录 什么是spring? spring是为了解决什么问题而衍生的?(历史)Spring解决了实际生产中的什么问题? spring包含了哪些部分?(组成) Spring的特点是什么? spring框架中…...
Qt交叉编译环境搭建
环境及版本: 编译机:Deepin 20.3 Qt 5.12.9 arm编译工具: gcc-linaro-6.5.0-2018.12-x86_64_arm-linux-gnueabihf.tar.xz 运行机:创龙335X开发板 1.下载arm编译工具: gcc-linaro-6.5.0-2018.12-x86_64_arm-linux-…...

Java switch case 语句
Java 的 switch case 语句是一种常用的控制流语句,用于基于不同的输入值执行不同的操作。本文将详细介绍 Java switch case 语句的作用、用法以及在实际工作中的应用。 一、switch case 语句的作用 switch case 语句是一种多分支条件语句,它基于不同的输…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
