[acwing周赛复盘] 第 93 场周赛20230304
[acwing周赛复盘] 第 93 场周赛20230304
- 一、本周周赛总结
- 二、 4867. 整除数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、 4868. 数字替换
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、4869. 异或值
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
- 彩笔了,只AC一题。
- T1模拟,整除向上取整。
- T2 BFS。这题应该是能AC的,但是一直TLE,就是样例都TLE,特判了也TLE。最后发现把前边一堆import删了就ac了。。看来import是加时间的。
- T3 分治/01字典树/异或字典树。
二、 4867. 整除数
链接: 4867. 整除数
1. 题目描述
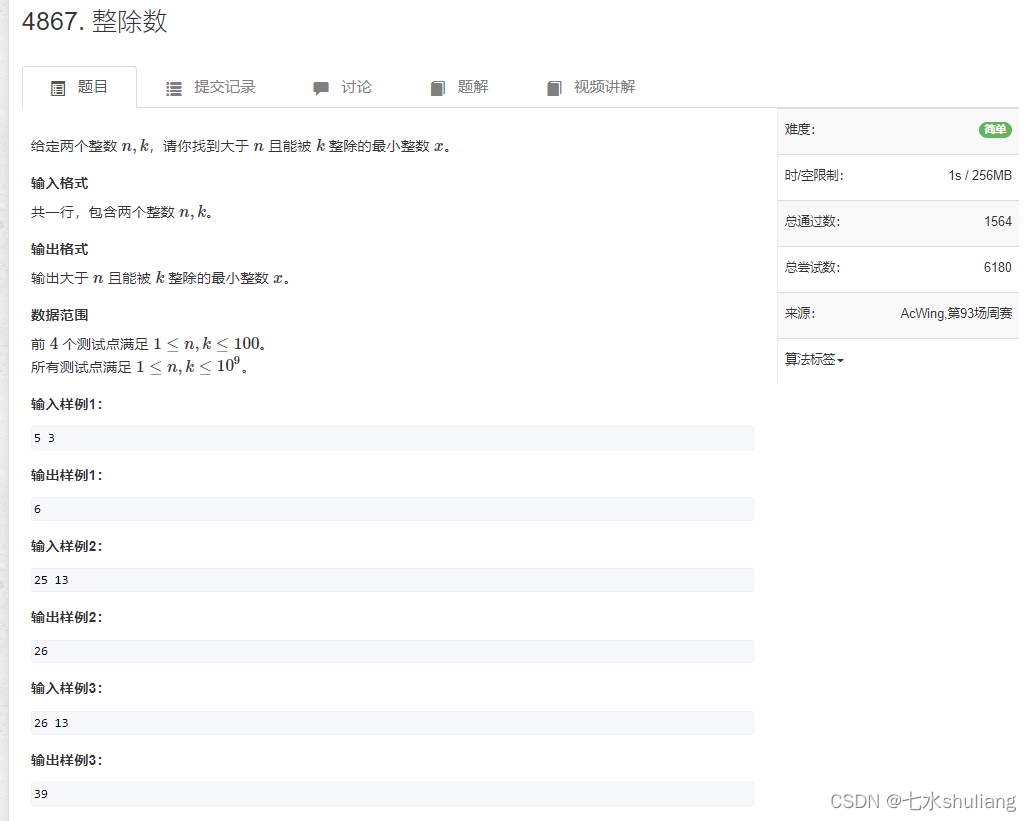
2. 思路分析
- 题目要求整除,且大于n,即最小是n+1的能整除k的数。显然是ceil((n+1) / k)
3. 代码实现
# Problem: 整除数
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4870/
# Memory Limit: 256 MB
# Time Limit: 1000 msimport sysRI = lambda: map(int, sys.stdin.buffer.readline().split())# ms
def solve():n, k = RI()n += 1print((n + k - 1) // k * k)if __name__ == '__main__':solve()
三、 4868. 数字替换
链接: 4868. 数字替换
1. 题目描述
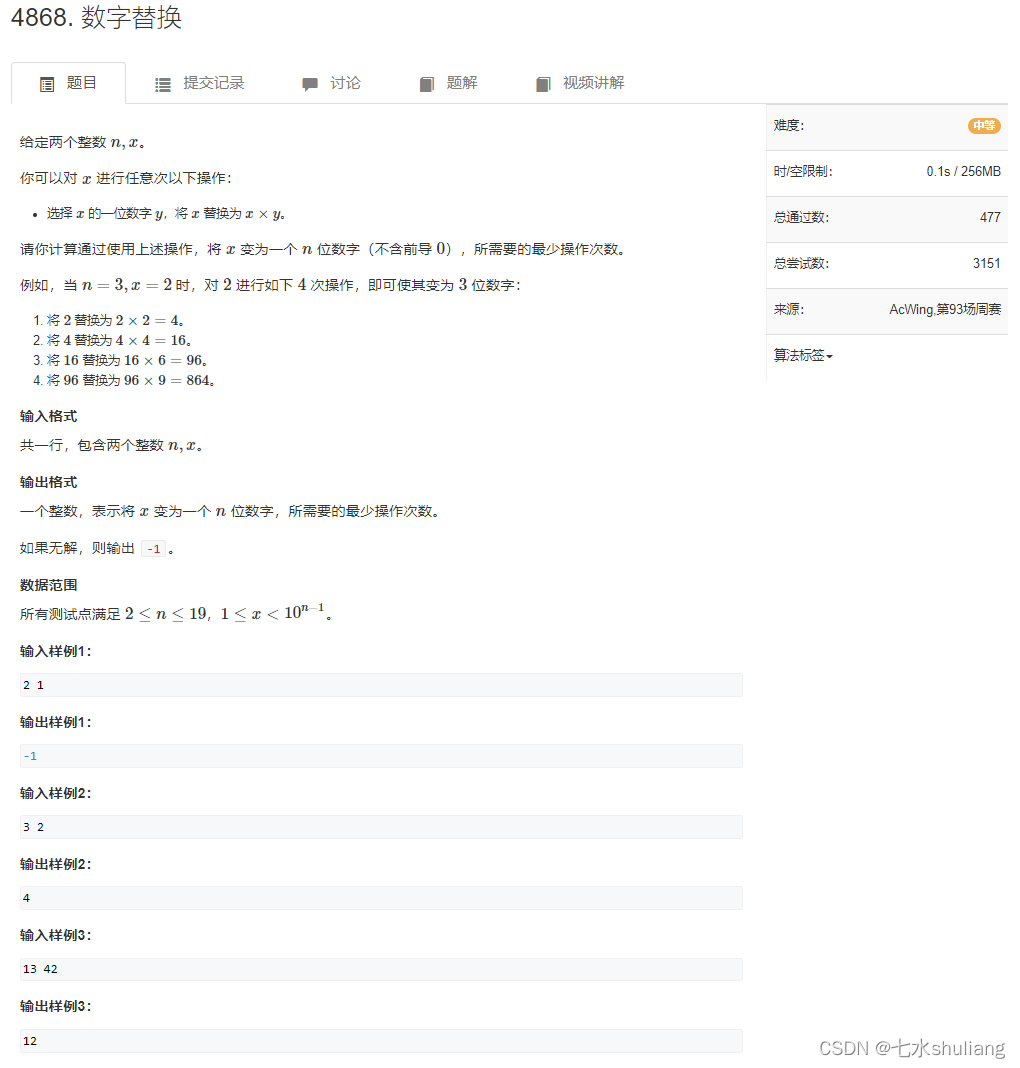
2. 思路分析
这题的教训是:如果在acw卡常,先把import都删干净!
- 看完题应该立刻想到一些特例,然后BFS即可。
- 特例:如果x是0或者1,那么n只能是1,否则返回-1.
- 如果x里有0,那么可以一步到一位数。
- 只有0才能让数字位数变小,且只能变到一位,特判一下存在0且n==1的情况
- 其它情况只要n<len(x) 一定无解。
- 然后bfs即可。
3. 代码实现
# Problem: 数字替换
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4871/
# Memory Limit: 256 MB
# Time Limit: 1000 msimport sys
from collections import *RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')# ms
def solve():n, x = RI()ans = 0s = str(x)if len(s) == n:return print(0)if '0' in s and n == 1:return print(1)if n < len(s):return print(-1)if max(s) == '1':return print(-1)q = deque([x])vis = {x}while q:ans += 1for _ in range(len(q)):x = q.popleft()s = str(x)for i in s:y = x * int(i)if len(str(y)) == n:return print(ans)if y not in vis:vis.add(y)q.append(y)print(-1)if __name__ == '__main__':solve()
四、4869. 异或值
链接: 4869. 异或值
1. 题目描述
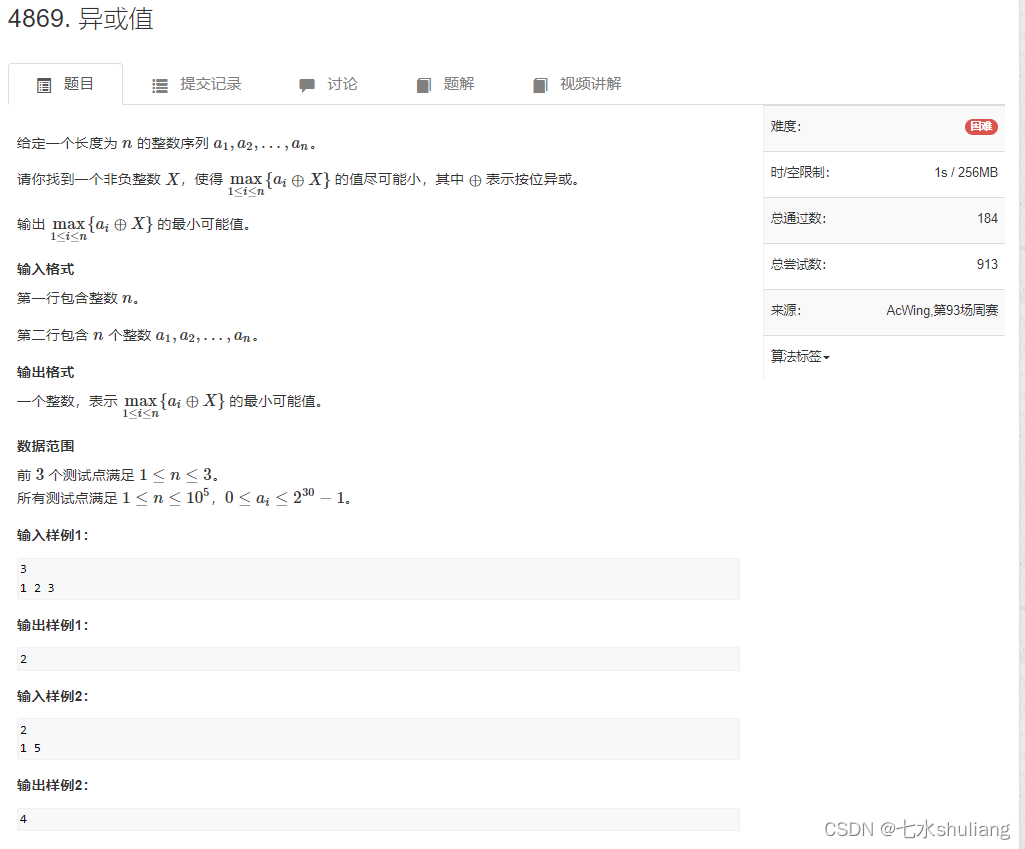
2. 思路分析
这题01字典树或者分治都可以。
- 其实应该立刻想到01字典树的,因为是批量异或的最大值问题。
- 假设我们要异或的数字是x,最终得到最大值是mx。
- 建完树后,从高位向下逐层考虑:
- 如果本层里只有1,那可以让x这一位是1,则mx的这一位可以是0。那么我们往1走,返回递归后的结果即可。
- 如果只有0,同理。往0走即可。
- 如果01都有,那么x这位无论是几,mx这位都会取到1,那么我们往01走都要试一下,取那个最小的;别忘记加上本层的1。
- 恶心之处在于,做这题时,用封装版的TLE了,拆出来后才过的,但也7000ms。
- 试了下,直接分治是更快的。1700ms。
- 直接按位考虑,把数字按本位01分组。讨论方法同上。
- 若只有1的组,那就递归1即可。
- 若只有0的组,递归0即可。
- 若都有,则mx这位必是1,递归两边取最小。
3. 代码实现
# Problem: 异或值
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4872/
# Memory Limit: 256 MB
# Time Limit: 1000 msimport sysRI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')MOD = 10 ** 9 + 7
PROBLEM = """
"""class TrieXor:def __init__(self, nums=None, bit_len=31):# 01字典树,用来处理异或最值问题,本模板只处理数字最低的31位# 用nums初始化字典树,可以为空self.trie = {}self.cnt = 0 # 字典树插入了几个值if nums:for a in nums:self.insert(a)self.bit_len = bit_lendef insert(self, num):# 01字典树插入一个数字num,只会处理最低bit_len位。cur = self.triefor i in range(self.bit_len - 1, -1, -1):nxt = (num >> i) & 1if nxt not in cur:cur[nxt] = {}cur = cur[nxt]cur[3] = cur.get(3, 0) + 1 # 这个节点被经过了几次cur[5] = num # 记录这个数:'#'或者'end'等非01的当key都行;这里由于key只有01因此用5self.cnt += 1def find_max_xor_num(self, num):# 计算01字典树里任意数字异或num的最大值,只会处理最低bit_len位。# 贪心的从高位开始处理,显然num的某位是0,对应的优先应取1;相反同理cur = self.trieret = 0for i in range(self.bit_len - 1, -1, -1):if (num >> i) & 1 == 0: # 如果本位是0,那么取1才最大;取不到1才取0if 1 in cur:cur = cur[1]ret += ret + 1else:cur = cur.get(0, {})ret <<= 1else:if 0 in cur:cur = cur[0]ret += ret + 1else:cur = cur.get(1, {})ret <<= 1return retdef find_max_xor_any(self):"""计算所有数字异或异或同一数字x时,结果里max的最小值"""def dfs(cur, bit): # 计算当前层以下能取到的最小的最大值if bit < 0:return 0if 0 not in cur: # 如果这层都是1,那么可以使x的这层是1,结果里的这层就是0,递归下一层即可。return dfs(cur[1], bit - 1)elif 1 not in cur: # 如果这层都是0,使x这层是0,递归下一层。return dfs(cur[0], bit - 1)# 如果01都有,那么x这层不管是几,结果最大值里这层都是1,那么考虑走1还是走0方向,取min后加上本层的值。return min(dfs(cur[0], bit - 1), dfs(cur[1], bit - 1)) + (1 << bit)return dfs(self.trie, self.bit_len - 1)def count_less_than_limit_xor_num(self, num, limit):# 计算01字典树里有多少数字异或num后小于limit# 由于计算的是严格小于,因此只需要计算三种情况:# 1.当limit对应位是1,且异或值为0的子树部分,全部贡献。# 2.当limit对应位是1,且异或值为1的子树部分,向后检查。# 3.当limit对应为是0,且异或值为0的子树部分,向后检查。# 若向后检查取不到,直接剪枝breakcur = self.trieans = 0for i in range(self.bit_len - 1, -1, -1):a, b = (num >> i) & 1, (limit >> i) & 1if b == 1:if a == 0:if 0 in cur: # 右子树上所有值异或1都是0,一定小于1ans += cur[0][3]cur = cur.get(1) # 继续检查右子树if not cur: break # 如果没有1,即没有右子树,可以直接跳出了if a == 1:if 1 in cur: # 右子树上所有值异或1都是0,一定小于1ans += cur[1][3]cur = cur.get(0) # 继续检查左子树if not cur: break # 如果没有0,即没有左子树,可以直接跳出了else:cur = cur.get(a) # limit是0,因此只需要检查异或和为0的子树if not cur: break # 如果没有相同边的子树,即等于0的子树,可以直接跳出了return ans# 封装成类卡常真是吐了 ms
def solve_tle():n, = RI()a = RILST()trie = TrieXor(bit_len=30)for x in a:trie.insert(x)ans = trie.find_max_xor_any()print(ans)# 7224 ms
def solve1():n, = RI()a = RILST()trie = {}for x in a:cur = triefor i in range(29, -1, -1):nxt = (x >> i) & 1if nxt not in cur:cur[nxt] = {}cur = cur[nxt]def dfs(cur, bit): # 计算当前层以下能取到的最小的最大值if bit < 0:return 0if 0 not in cur: # 如果这层都是1,那么可以使x的这层是1,结果里的这层就是0,递归下一层即可。return dfs(cur[1], bit - 1)elif 1 not in cur: # 如果这层都是0,使x这层是0,递归下一层。return dfs(cur[0], bit - 1)# 如果01都有,那么x这层不管是几,结果最大值里这层都是1,那么考虑走1还是走0方向,取min后加上本层的值。return min(dfs(cur[0], bit - 1), dfs(cur[1], bit - 1)) + (1 << bit)ans = dfs(trie, 29)print(ans)# 1725 ms
def solve():n, = RI()a = set(RILST())def dfs(a, bit): # 计算当前层以下能取到的最小的最大值if bit < 0:return 0x, y = [], []t = 1 << bitfor v in a:if v & t:x.append(v)else:y.append(v)if not x: return dfs(y, bit - 1)if not y: return dfs(x, bit - 1)# 如果01都有,那么x这层不管是几,结果最大值里这层都是1,那么考虑走1还是走0方向,取min后加上本层的值。return min(dfs(x, bit - 1), dfs(y, bit - 1)) + tprint(dfs(a, 29))if __name__ == '__main__':solve()六、参考链接
- 无
相关文章:

[acwing周赛复盘] 第 93 场周赛20230304
[acwing周赛复盘] 第 93 场周赛20230304 一、本周周赛总结二、 4867. 整除数1. 题目描述2. 思路分析3. 代码实现三、 4868. 数字替换1. 题目描述2. 思路分析3. 代码实现四、4869. 异或值1. 题目描述2. 思路分析3. 代码实现六、参考链接一、本周周赛总结 彩笔了,只A…...

NOIP2022 T4 比赛
P8868 [NOIP2022] 比赛 题目大意 有两个长度为nnn的序列aaa和bbb,有qqq次询问,每次询问给出l,rl,rl,r,求 ∑ilr∑ji1r(maxkijak)(maxlijbl)\sum\limits_{il}^r\sum\limits_{ji1}^r(\max\limits_{ki}^ja_k)\times(\max\limits_{li}^jb_l…...
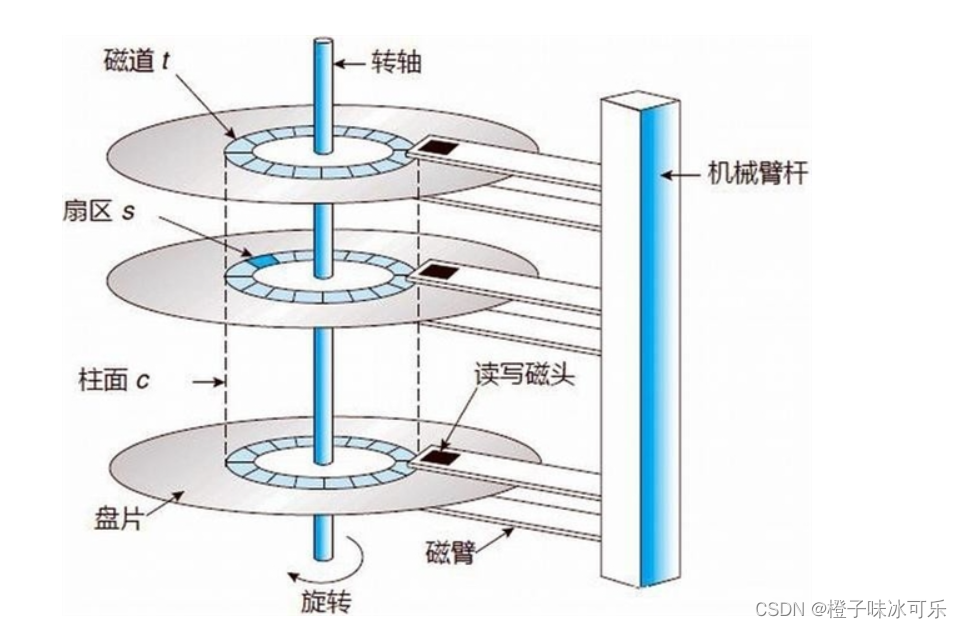
计算机组成原理
目录 ❤ 控制器 ❤ 运算器 ❤ 控制器运算器(计算机的中央处理器CPU) ❤ 存储器 内存(主存) 外存 内存和外村的区别 ❤ 输入设备 ❤ 输出设备 ❤ 适配器 ❤ 总线 ❤ 启动计算机的流程 ❤ 机械硬盘 ❤ 固态硬盘 python从小白到总裁完整教程目录:https://b…...

1. 命名规范
1. 命名规范 成绩10开启时间2021年09月17日 星期五 18:00折扣0.8折扣时间2021年11月6日 星期六 00:00允许迟交否关闭时间2021年11月21日 星期日 00:00 家有家法,行有行规。在家有家的规矩,入行有行的规矩。我们计算机一行就有一个命名的规矩,…...

论文投稿指南——中文核心期刊推荐(新闻事业)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
【Linux】工具(4)——make/Makefile
本期博客我们的任务就是搞懂自动化构建工具——make/Makefile一、什么是make/Makefile📌make是一个命令工具,是一个解释makefile中指令的命令工具,一般来说,大多数的IDE都有这个命令,比如:Delphi的make&…...
【企业服务器LNMP环境搭建】nginx安装
1、介绍(官方网址:nginx news ) 1.1 常见用法 1) web服务器软件 httpd http协议 同类的web服务器软件:apache nginx(俄罗斯) IIS(微软 fastcgi) lighttpd(德国) 2)代理服务器 反向代理 3)邮箱代理服务器 IMAP POP3 SMTP 4)负载均…...

Linux 配置规范 操作系统 _S3A3G3
目录 1.检查使用IP协议远程维护的设备是否配置SSH协议,禁用telnet协议 2.检查账户认证失败次数限制...
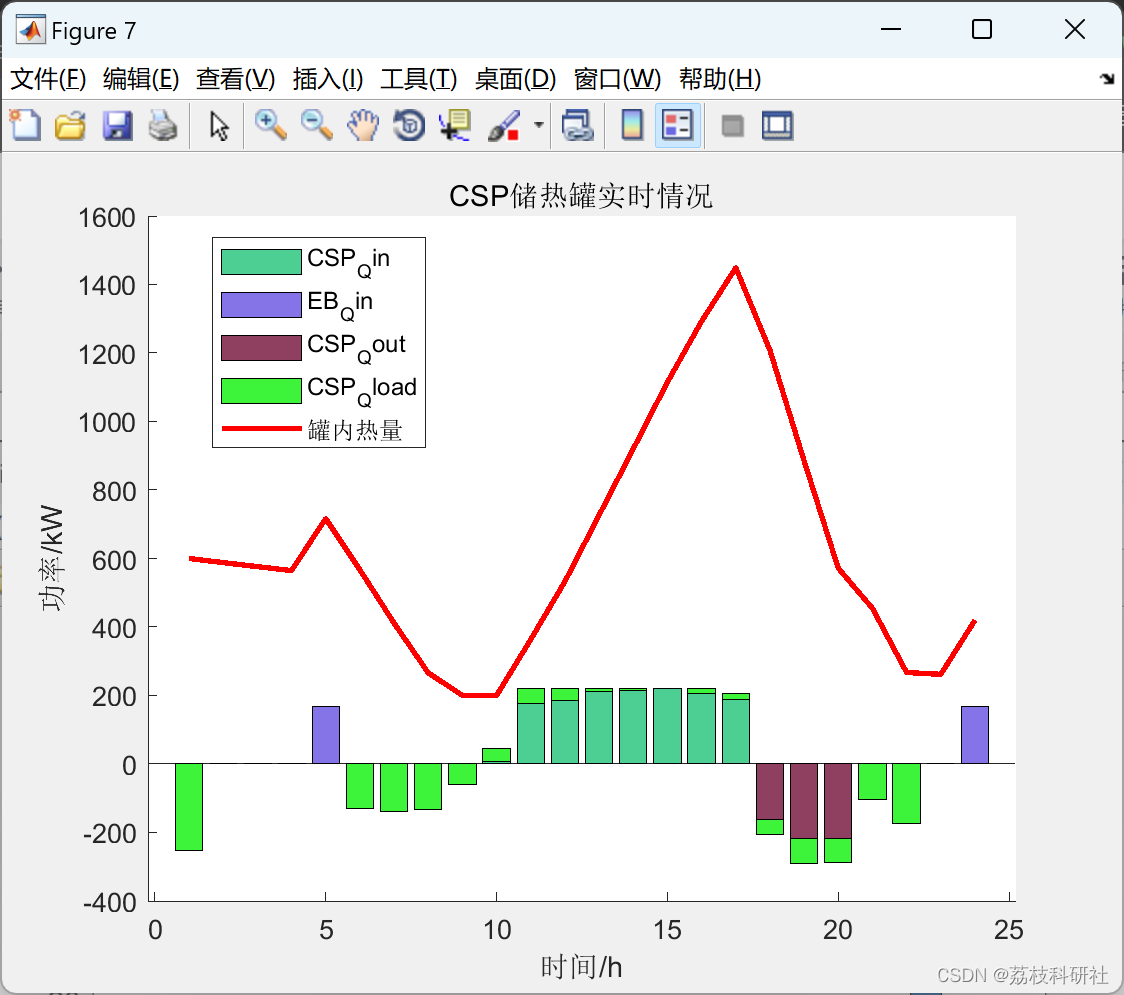
基于信息间隙决策理论的碳捕集电厂调度(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【C语言进阶:指针的进阶】回调函数
本章重点内容: 字符指针指针数组数组指针数组传参和指针传参函数指针函数指针数组指向函数指针数组的指针回调函数指针和数组面试题的解析什么是回调函数: 回调函数就是一个通过函数指针调用的函数。如果你把函数的指针(地址)作…...

C++模板的使用
在平时的工作和学习过程中,经常会用到泛型,这里对泛型和模板进行一下梳理,以便理解和使用。 模板关键字 template。为什么要使用模板? 假如设计一个两个参数的函数,用来求两个对象的乘积,在实践中我们可能需要定义n多个函数 int multipli…...

三天Golang快速入门—面向对象
面向对象Golang接口的定义go中类空接口空接口作为函数的参数切片实现空接口map的值实现空接口类型断言值接收者和指针接收者值接收者指针接收者接口嵌套Golang接口的定义 接口interface是一种抽象的类型。接口定义了一个对象的行为规范,只定义规范不实现࿰…...

开发手册——一、编程规约_6.并发处理
这篇文章主要梳理了在java的实际开发过程中的编程规范问题。本篇文章主要借鉴于《阿里巴巴java开发手册终极版》 下面我们一起来看一下吧。 1. 【强制】获取单例对象需要保证线程安全,其中的方法也要保证线程安全。 说明:资源驱动类、工具类、单例工厂…...

ACM---大一第三周周赛(Floyd算法+并查集算法学习周)
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...
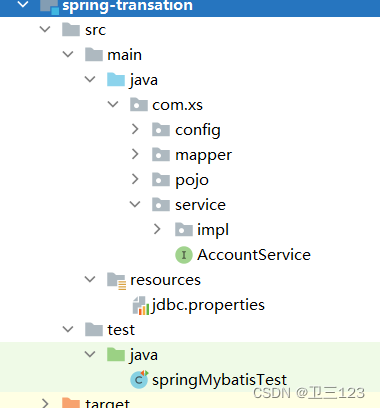
spring整合mybatis和Junit
该项目使用spring纯注解方式开发,用配置类取代spring的配置文件 一、导入依赖 整合Junit需要导入spring-test 整合mybatis需要导入spring-jdbc、mybatis-spring <dependencies><!-- https://mvnrepository.com/artifact/org.springframework/spring-cont…...

Spring Boot 3.0系列【7】核心特性篇之JSON
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot版本3.0.3 源码地址:https://gitee.com/pearl-organization/study-spring-boot3 文章目录 前言JSON什么是JSON常用JSON 库GsonFastJsonJacksonJackson 还是 FastjsonSpring Boot 中的 JSON1. 自动配置 Jackson2. @…...
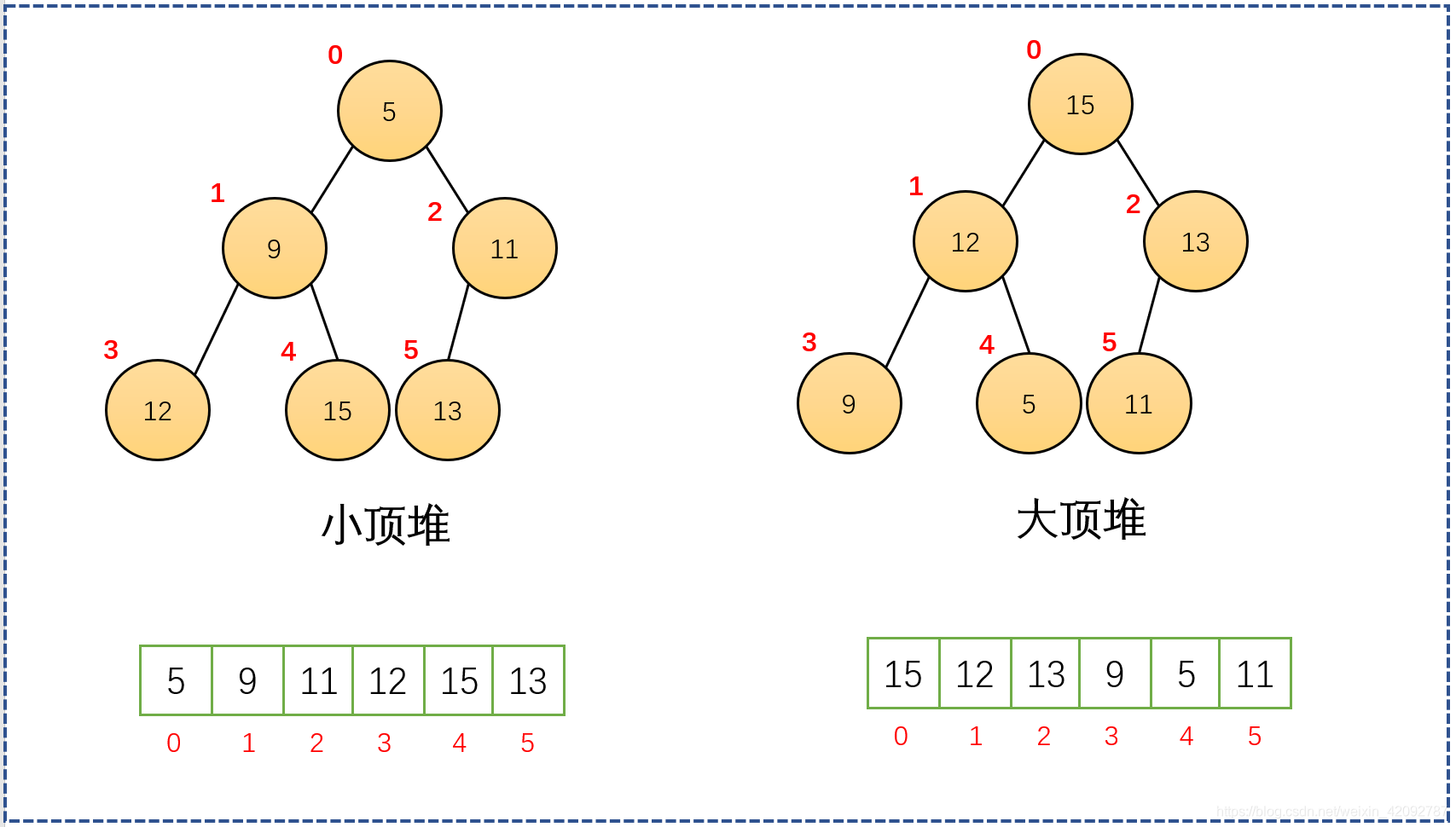
【数据结构初阶】二叉树顺序结构:堆的实现
前言 前边077带着大家学习了树与二叉树的相关概念,这篇文章我们来实现一个二叉树的顺序结构。 二叉树的顺序结构 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉…...
C/C++:动态内存管理
目录 一. C/C内存分布 二. C/C动态内存管理 2.1 C语言动态内存管理 2.2 C动态内存管理 2.2.1 new/delete操作符 2.2.2 operator new与operator delete函数 2.3 new/delete的实现原理 2.4 定位new(placement - new) 2.5 new/delete和malloc/free的…...
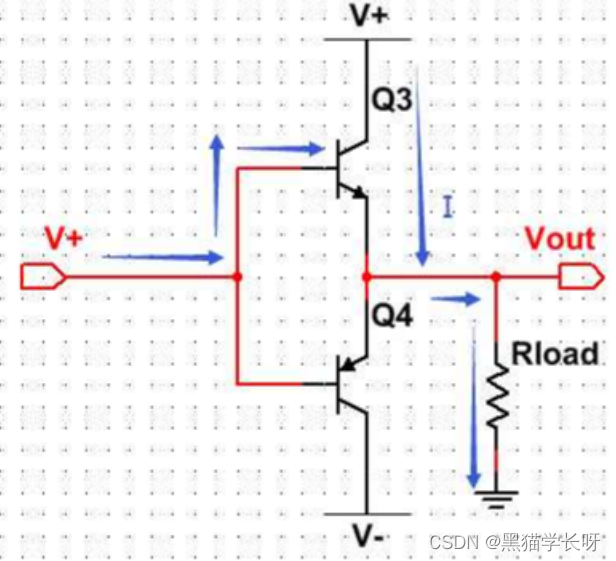
黑猫带你学eMMC协议第28篇:eMMC的开漏和推挽模式(push-pull open drain)
本文依据eMMC JEDEC5.1及个人工作经验整理而成,如有错误请留言。 文章为个人辛苦整理,付费内容,已加入原创侵权保护,禁止私自转载。 文章所在专栏:《黑猫带你学:eMMC协议详解》 1 什么是开漏和推挽 1.1 推挽电路是什么 关于推挽和开漏电路,更多介绍详见我的另一篇文章…...
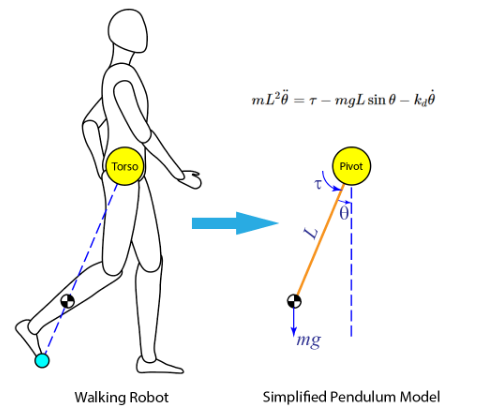
simulink PID控制
系列文章目录 文章目录系列文章目录前言一、非线性系统线性化原理二、反馈控制开环控制反馈or闭环控制PID ControllerPID微调案例总结前言 将非线性系统近似线性化PIDblock与微调 提示:以下是本篇文章正文内容,下面案例可供参考 一、非线性系统线性化 …...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...
