【算法基础 数学】快速幂
题目描述
给定 n n n组 a i , b i , p i a_i,b_i,p_i ai,bi,pi,对于每组数据,求出 a i b i m o d p i a_i^{b^i}~mod~p_i aibi mod pi 的值。
样例
输入样例:
2
3 2 5
4 3 9
输出样例:
4
1
快速幂解决的问题
用来解决快速的求解 a k m o d a^k~mod ak mod p p p的结果
时间复杂度为 O ( l o g k ) O(logk) O(logk)
原理(反复平方法)
预处理出来这些值:
a 2 0 m o d p a^{2^0}~mod~p a20 mod p
a 2 1 m o d p a^{2^1}~mod~p a21 mod p
a 2 2 m o d p a^{2^2}~mod~p a22 mod p
. . . ... ...
a 2 l o g k m o d p a^{2^{logk}}~mod~p a2logk mod p
大概是logk个
则 a k a^k ak可以表示为前面分解的这些数的某些数的乘积
则 k k k可以表示为 2 2 2的若干次幂的和
(利用k的二进制表示)
a k = a 2 x 1 a 2 x 2 . . . a 2 x t = a 2 x 1 + 2 x 2 + . . . + 2 x t a^k =a^{2^{x_1}}a^{2^{x_2}}...a^{2^{x_t}} =a^{2^{x_1}+2^{x_2}+...+2^{x_t}} ak=a2x1a2x2...a2xt=a2x1+2x2+...+2xt
如何求 a x a^x ax?
a 1 = a a^1~=~a a1 = a
a 2 1 = ( a 1 ) 2 a^{2^1}~=~(a^{1})^2 a21 = (a1)2
a 2 2 = ( a 2 1 ) 2 a^{2^2}~=~(a^{2^1})^2 a22 = (a21)2
. . . ... ...
a 2 l o g k = ( a 2 l o g k − 1 ) 2 a^{2^{logk}}~=~(a^{2^{logk}-1})^2 a2logk = (a2logk−1)2
也就是说,后一个数都是前一个数的平方
也就是经过k次迭代,就可以把这些数分解出来了
其实就是看k的二进制表示里面,哪些位是1,把1对应的这些位对应的数乘起来就可以了
代码
#include<iostream>
#include<algorithm>
using namespace std;typedef long long LL;LL qmi(int a, int k, int p){LL res = 1 % p;while(k){if(k & 1) res = res * a % p; //如果最后一位是1,乘上a^2^a%pa = a * (LL)a % p; //a向后迭代,继续平方k >>= 1; //把k的最后以为删掉}return res;
}int main(){int n, a, b, p;cin >> n;while(n--){scanf("%d%d%d", &a, &b, &p);printf("%lld\n", qmi(a, b, p));}return 0;
}
作者:为梦而生
链接:https://www.acwing.com/solution/content/220897/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

【算法基础 数学】快速幂
题目描述 给定 n n n组 a i , b i , p i a_i,b_i,p_i ai,bi,pi,对于每组数据,求出 a i b i m o d p i a_i^{b^i}~mod~p_i aibi mod pi 的值。 样例 输入样例: 2 3 2 5 4 3 9输出样例: 4 1快速幂解决的问题 用来…...

2024年华为OD机考高分攻略-完整题库-两周350分
华为OD是个不错的机会,很适合非软件行业到软件行业的转身。 但是很多同学之前没有软件基础,不知道该如何高效的准备OD机考。 我是一名软件培训老师,我的学生有上百人顺利通过了华为OD机考,并取得了高分,我将经验分享…...

【微信小程序独立开发 4】基本信息编辑
这一节完成基本信息的编辑和保存 首先完成用户头像的获取 头像选择 需要将 button 组件 open-type 的值设置为 chooseAvatar,当用户选择需要使用的头像之后,可以通过 bindchooseavatar 事件回调获取到头像信息的临时路径。 从基础库2.24.4版本起&…...

Docker-基础指令
前置知识 docker官网地址:https://www.docker.com/ docker镜像地址:https://hub.docker.com/ docker安装教程:https://docs.docker.com/engine/install/centos/ 安装只需要注意将仓库源改为国内就好,推荐去阿里云注册自己的账号获得加速地址…...
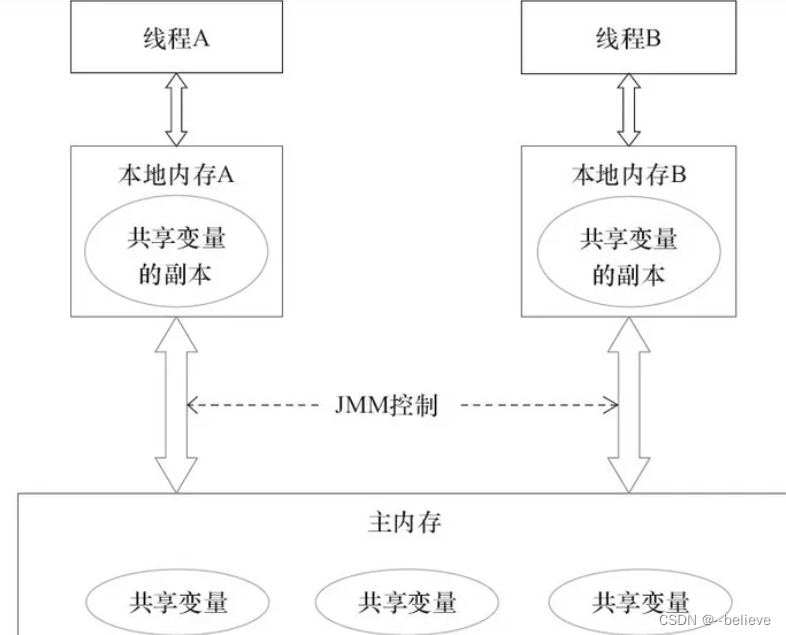
JUC-Java内存模型JMM
JMM概述 Java Meory Model java内存模型。在不同的硬件和不同的操作系统上,对内存的访问方式是不一样的。这就造成了同一套java代码运行在不同的操作系统上会出问题。JMM就屏蔽掉硬件和操作系统的差异,增加java代码的可移植性。这是一方面。 另一方面JM…...

uni-app使用HBuilderX打包Web项目
非常简单,就是容易忘记 一、找到manifest.json配置Web配置 二、源码视图配置 "h5" : {"template" : "","domain" : "xxx.xx.xx.xxx","publicPath" : "./","devServer" : {&quo…...

前后置、断言、提取变量、数据库操作功能
前置操作和后置操作都是 API 请求在发送和响应过程中执行的脚本,主要用于在发起 API 请求前和获得响应后完成验证或执行某些操作,目的是为了提高 API 调试和测试的效率,并确保接口的正确性。 前置操作 前置操作是在 API 请求之前执行的脚本…...
)
三子棋/井字棋(C语言)
这个游戏需要用到三个文件 game.h头文件用来申明函数和导包 game.h如下: #pragma once #define ROW 3 #define COL 3 #include <stdlib.h> #include <time.h> #include <stdio.h>//初始化棋盘的函数void InitBoard(char board[ROW][COL], int row, int co…...

数据结构小项目----通讯录的实现(这里用链表实现) 超详细~~~~૮(˶ᵔ ᵕ ᵔ˶)ა
目录 Contact.h说明: 结构体与头文件的包含: 编辑 函数在头文件的声明与定义: Contact.c中各个函数的实现: 1.检查链表中的数据是否满了,满了就扩容 2.链表的尾插 3.链表的删除 4.查找名字是否匹配 5.初始化通讯…...
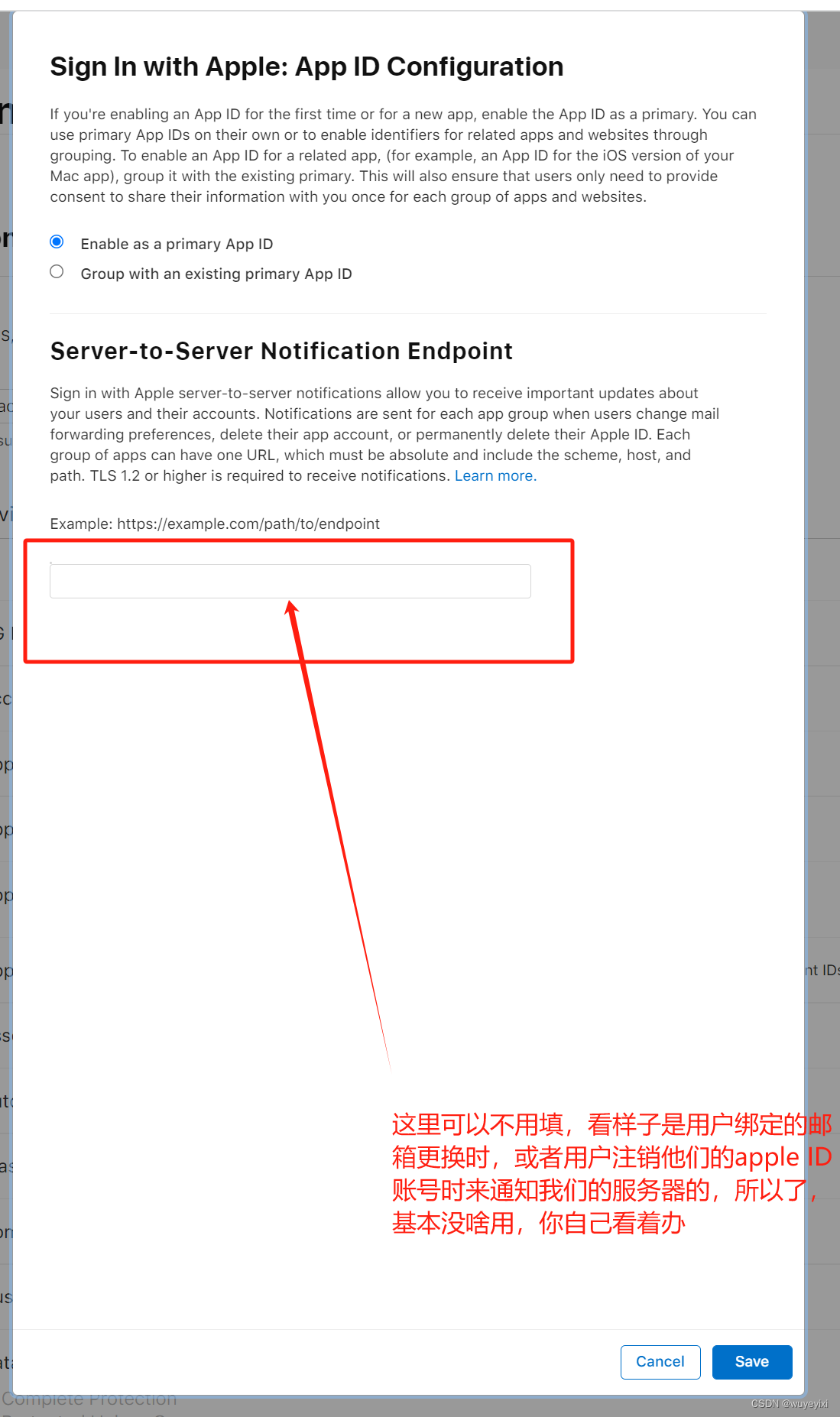
Electron Apple SignIn 登录
本人写博客,向来主张:代码要完整,代码可运行,文中不留下任何疑惑。 最讨厌写博客,代码只留下片段,文中关键的东西没写清楚。之前看了那么多文章,就是不告诉我clientId从哪来的。 官方资料地址&…...
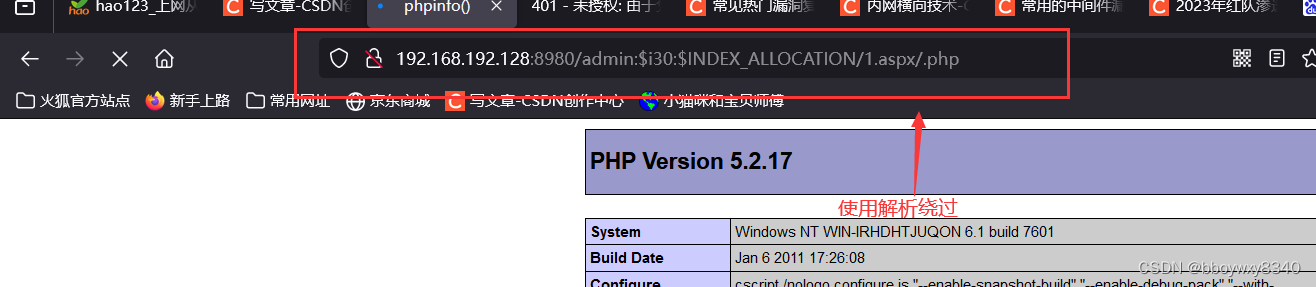
常用中间件漏洞
IIS6 IIS7 安装 控制面板-----打开关闭windows功能 添加角色-----添加IIS 启动之后访问localhost 复现 服务器换成IIS7 访问报错 大概就是缺少CGI模块 问题解决 添加php-cgi的路径 添加脚本映射 修改php.ini文件 将 cgi.fix_pathinfo1 然后设置一个图片 访问 在后缀加上/.…...

Windows系统使用手册
点击前往查看🔗我的博客文章目录 Windows系统使用手册 文章目录 Windows系统使用手册Windows10解决大小核调度问题Windows系统安装软件Windows系统Typora快捷键Windows系统压缩包方式安装redisWindows安装dockerWindows系统的docker设置阿里源Windows系统下使用doc…...
mp4文件可以转成mp3音频吗
现在是个非常流行刷短视频一个年代,刷短视似乎成了人们休闲娱乐的一种方式,在日常刷短视频过程中,肯定会有很多同学被短视频 bgm 神曲洗脑,比如很多被网红翻唱带火的歌曲,例如其中"不负人间”,就是其中…...

Java-IO流【登录注册小项目】
♥️作者:白日参商 🤵♂️个人主页:白日参商主页 ♥️坚持分析平时学习到的项目以及学习到的软件开发知识,和大家一起努力呀!!! 🎈🎈加油! 加油!…...

数字化金融时代:探讨全球金融科技创新的最新动态
在当今数字化金融时代,金融科技创新如影随形,迅猛发展。本文将深入探讨全球范围内金融科技的最新动态,剖析各地新兴趋势与突破。从区块链技术的应用到人工智能在金融领域的崭露头角,我们将一一解读这个正在不断演变的金融科技画卷…...

LeetCode:206. 反转链表
力扣链接 算法思想:由于单链表是单向的,想要对当前元素进行操作,需找到前一个元素。本题利用双指针,初始pre指针指向NULL,cur指针指向head.再对局部翻转之前,先把下一个结点存到temp指针中。当进行完如下代…...
linux 安装nginx
介绍 官网 https://nginx.org/en/download.html 在安装nginx前首先要确认系统中安装了gcc、pcre-devel、zlib-devel、openssl-devel linux 检查是否安装过某软件包 yum -y install gcc pcre-devel zlib-devel openssl openssl-devel #下载 wget https://nginx.org/downloa…...

1.C语言——基础知识
C语言基础知识 1.第一个C语言程序2.注释3.标识符4.关键字5.数据类型6.变量7.常量8.运算符9.输入输出输入输出 1.第一个C语言程序 C语言的编程框架 #include <stdio.h> int main() {/* 我的第一个 C 程序 */printf("Hello, World! \n");return 0; }2.注释 单行…...

Redis 存在线程安全问题吗?为什么?
一个工作了 5 年的粉丝私信我。 他说自己准备了半年时间,想如蚂蚁金服,结果第一面就挂了,非常难过。 问题是: “Redis 存在线程安全问题吗?” 一、问题解析 关于这个问题,我从两个方面来回答。 第一个&a…...

无人机测绘助力实现高效、安全的城市规划
随着城市化进程的不断加快,城市规划显得尤为重要。而无人机测绘技术作为一种创新的工具,为城市规划提供了更加高效、安全的解决方案。它通过快速、精确的数据采集和分析,为行业提供有力的决策支持,助力城市规划的现代化和可持续发…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
