当前位置： 首页 > news >正文

向量和向量如何相乘？

news 2026/2/10 11:56:11

向量与向量相乘主要有两种方式：点积（内积）和叉积（外积）。这两种运算的结果和应用是不同的。

点积（内积）：
点积是两个向量的对应元素相乘后再求和的结果，通常用于计算两个向量的相似度。点积的结果是一个标量。

例子：
在这里插入图片描述

叉积（外积）：
叉积是定义在三维向量上的运算，结果是一个新的向量，垂直于原来两个向量所构成的平面。叉积的大小表示原来两个向量组成的平行四边形的面积。

例子：
在这里插入图片描述
点积通常用于测量向量在方向上的投影，而叉积则用于求解与两个向量垂直的向量。

相关文章：

向量和向量如何相乘？

向量与向量相乘主要有两种方式：点积（内积）和叉积（外积）。这两种运算的结果和应用是不同的。 点积（内积）： 点积是两个向量的对应元素相乘后再求和的结果，通常用于计算两个…...

编程日记 2024/1/22 5:19:06

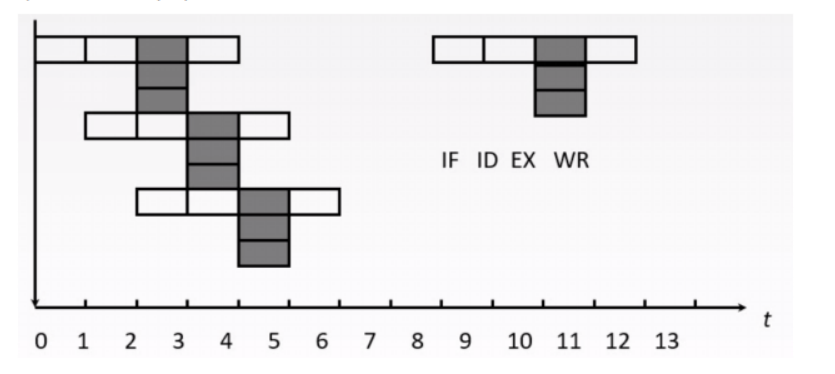
计算机组成原理 指令流水线

文章目录 指令流水线指令流水线的概念流水线性能分析流水线的吞吐率流水线的加速比流水线的效率 影响流水线的因素结构相关 (资源冲突)数据相关 (数据冲突)控制相关 (控制冲突) 流水线分类超量流水线 指令流水线 #mermaid-svg-sWaRASMFAvh8sLJk {font-family:"trebuchet m…...

编程日记 2024/1/22 5:18:04

macOS - md5 | md5sum

文章目录 简单使用介绍文档Linux - md5summacOS - md5 大文件传输是否完整，你可以使用 md5 进行校验 linux 上使用 md5sum 命令，在macOS 上 md5 命令是和 md5sum 等效的 简单使用介绍 参考：https://blog.csdn.net/cnds123321/article/detail…...

编程日记 2024/1/22 5:13:59

Tomcat快速入门

1.Tomcat介绍 Apache Tomcat 是由 Apache Software Foundation（ASF）开发的一个开源 Java WEB 应用服务器，如apache处理静态HTML能力突出不同，tomcat处理动态HTML能力相当强大，因此一般项目都是部署apachetomcat&#…...

编程日记 2024/1/22 5:10:57

如何结合antd design pro 5 结合express 上传多个文件

在Ant Design Pro 5（基于React）的前端界面结合Express后端实现上传整个文件夹的文件，实际上是在前端进行多文件选择，并通过POST请求将文件列表发送到后端，然后由后端处理上传。由于浏览器API限制，直接上传整…...

编程日记 2024/1/22 5:08:55

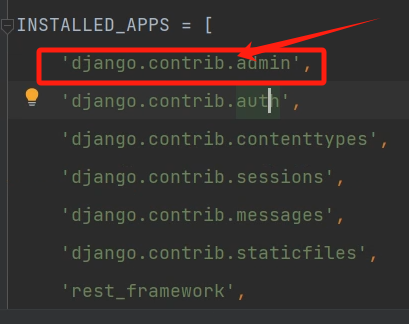
Django随笔

关于Django的admin 1. 在url中把 from django.contrib import admin 重新解开 把path(admin/,admin.site.urls), 解开 2. 注册app，在配置文件中写 django.contrib.admin, 3.输入命令进行数据库迁移 Django国际化 配置文件中（改成中文） LA…...

编程日记 2024/1/22 5:05:53

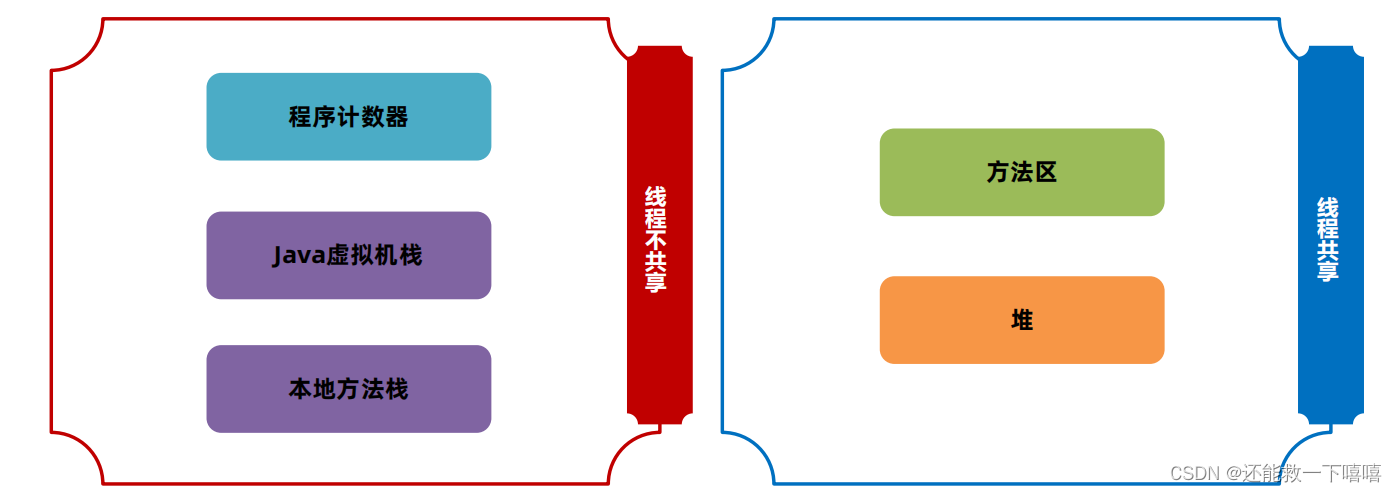
线程和进程的区别（从JVM角度出发）

进程与线程的区别 线程具有许多传统进程所具有的特征，故又称为轻型进程(Light—Weight Process)或进程元；而把传统的进程称为重型进程(Heavy—Weight Process)，它相当于只有一个线程的任务。在引入了线程的操作系统中，通常一个进…...

编程日记 2024/1/22 5:02:50

手把手教你如何快速定位bug,如何编写测试用例,快来观摩......

手把手教你如何快速定位bug,如何编写测试用例,快来观摩......手把手教你如何快速定位bug,如何编写测试用例,快来观摩......作为一名测试人员如果连常见的系统问题都不知道如何分析，频繁将前端人员问题指派给后端人员，后端人员问题指派给前端人员&#xf…...

编程日记 2024/1/22 5:01:49

计算矩阵边缘元素之和(c++)

题目描述 输入一个整数矩阵&#xff0c;计算位于矩阵边缘的元素之和。所谓矩阵边缘的元素&#xff0c;就是第一行和最后一行的元素以及第一列和最后一列的元素。 输入格式 第一行分别为矩阵的行数 和列数 &#xff08;m<100&#xff0c;n<100&#xff09;&#xff0c…...

编程日记 2024/1/22 4:59:47

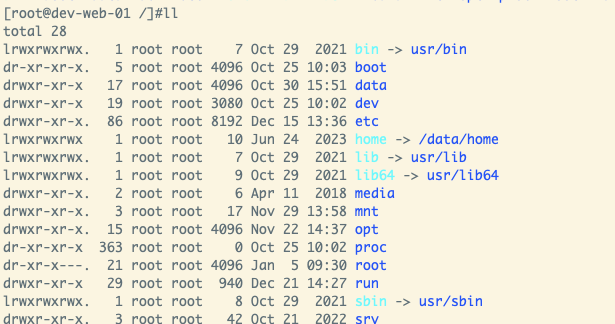
java使用jsch处理软链接判断是否文件夹

前言 这一次主要是碰到一个问题。因为使用jsch去读取文件的时候&#xff0c;有一些文件它是使用软链接制作的一个映射。因为这里面有一个问题。如果它是软链接你就无法判断他到底是文件。还是文件夹&#xff1f;因为他没有提供可以直接读取的方法&#xff0c;用权限信息去判断…...

编程日记 2024/1/22 4:56:45

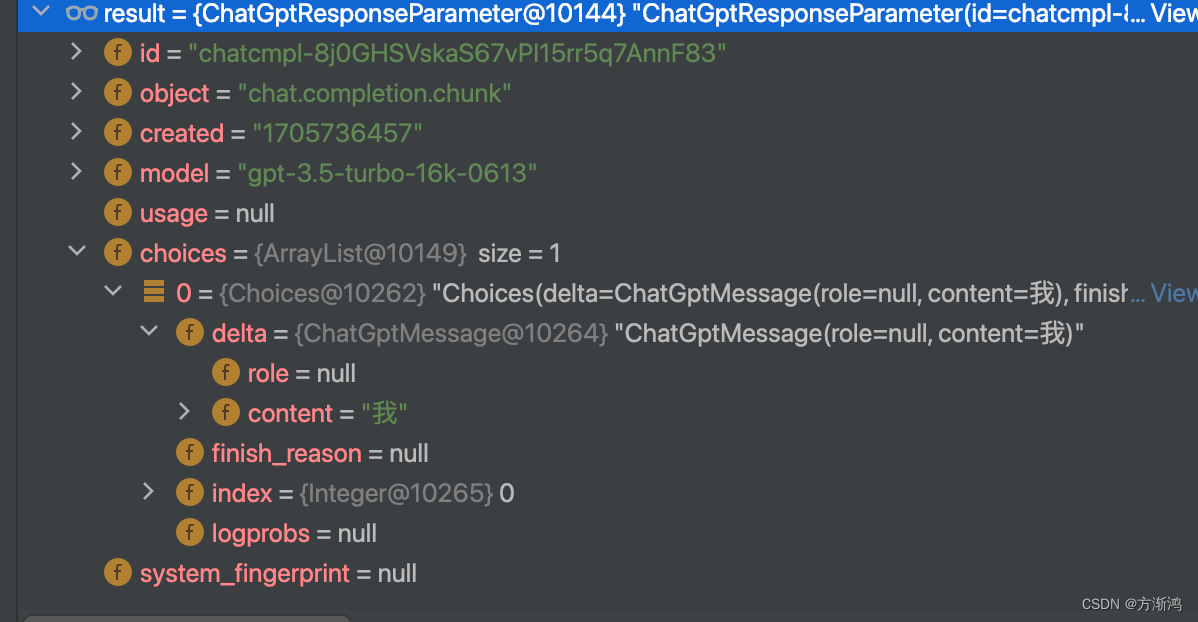
【2023】java使用WebClient实现chatGPT调用建立web socket连接

&#x1f4bb;目录 一、介绍1、使用技术2、效果 二、代码1、前端代码2、后端代码2.1、maven依赖2.2、model2.2.1、请求接口的格式2.2.2、响应数据对象 2.3、工具类2.3.1、&#x1f534;使用WebClient调用chatgpt方法2.3.2、&#x1f7e0; webSocket连接对话方法 2.4、Controlle…...

编程日记 2024/1/22 4:55:44

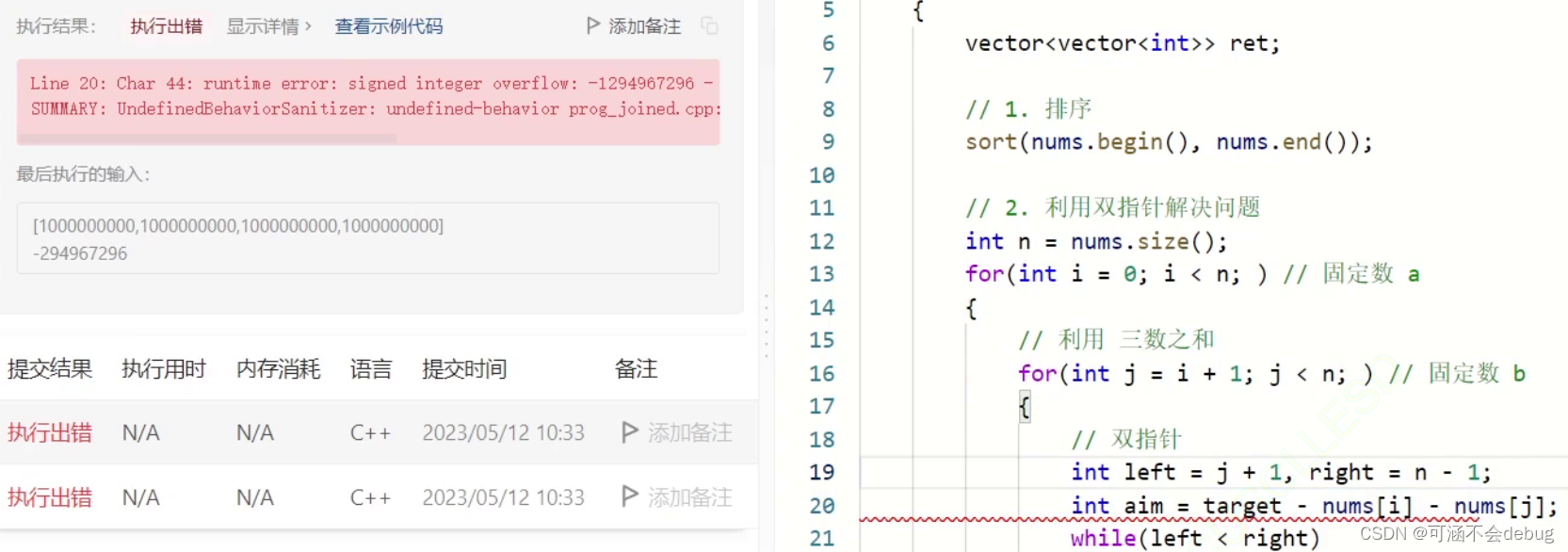
力扣【四数之和】

一、题目描述 18. 四数之和 给你一个由 n 个整数组成的数组 nums &#xff0c;和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] &#xff08;若两个四元组元素一一对应&#xff0c;则认为两个四元组重复&#x…...

编程日记 2024/1/22 4:54:43

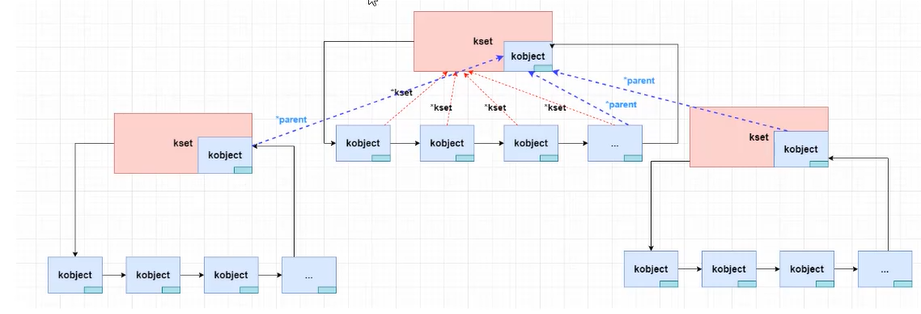
IMX6LL|linux设备驱动模型

linux设备驱动模型 为什么需要设备驱动模型 早期内核&#xff08;2.4之前&#xff09;没有统一的设备驱动模型&#xff0c;但照样可以用2.4~2.6期间使用devfs&#xff0c;挂载在/dev目录。 需要在内核驱动中创建设备文件(devfs_register)&#xff0c;命名死板 2.6以后使用sys…...

编程日记 2024/1/22 4:51:39

2023年的技术总结和工作反思

一、回顾2023年 回顾自己的2023年&#xff0c;还是发生了很多的变化。在大学毕业&#xff0c;就来到了芯翼参加工作&#xff0c;在这里也遇到了很多的前辈和小伙伴&#xff0c;收获工作的同时也收获了友情。但是&#xff0c;随着公司发展战略的变化&#xff0c;公司的人员架构…...

编程日记 2024/1/22 4:49:37

Stable Diffusion中的Embeddings

什么是Embeddings&#xff1f; Embeddings是一种数学技术&#xff0c;它允许我们将复杂的数据&#xff08;如文本或图像&#xff09;转换为数值向量。这些向量是高维空间中的点&#xff0c;可以捕捉数据的关键特征和属性。在文本处理中&#xff0c;例如&#xff0c;embeddings可…...

编程日记 2024/1/22 4:46:35

如何快速打开github

作为一个资深码农&#xff0c;怎么能不熟悉全球最大的同性交友社区——github呢&#xff0c;但头疼的是github有时能打开&#xff0c;有时打不开&#xff0c;这是怎么回事&#xff1f; 其实问题出在github.com解析DNS上&#xff0c;并不是需要FQ。下面提供一个方法&#xff0c;…...

编程日记 2024/1/22 4:45:34

【sql/python】表中某列值以列表聚合

需求背景&#xff1a; 有一个表含有两个字段 “ID”,“VALUE” 1,香蕉 1,苹果 2,橘子 3,香蕉 3,苹果 3,橘子 目标要求&#xff1a;将每个ID的VALUE列聚合成一个字符串列表 “ID”,“VALUE” 1,[香蕉,苹果] 2,[橘子] 3,[香蕉,苹果,橘子] 一、SQL使用 LISTAGG函数聚合方式 ---将…...

编程日记 2024/1/22 4:42:31

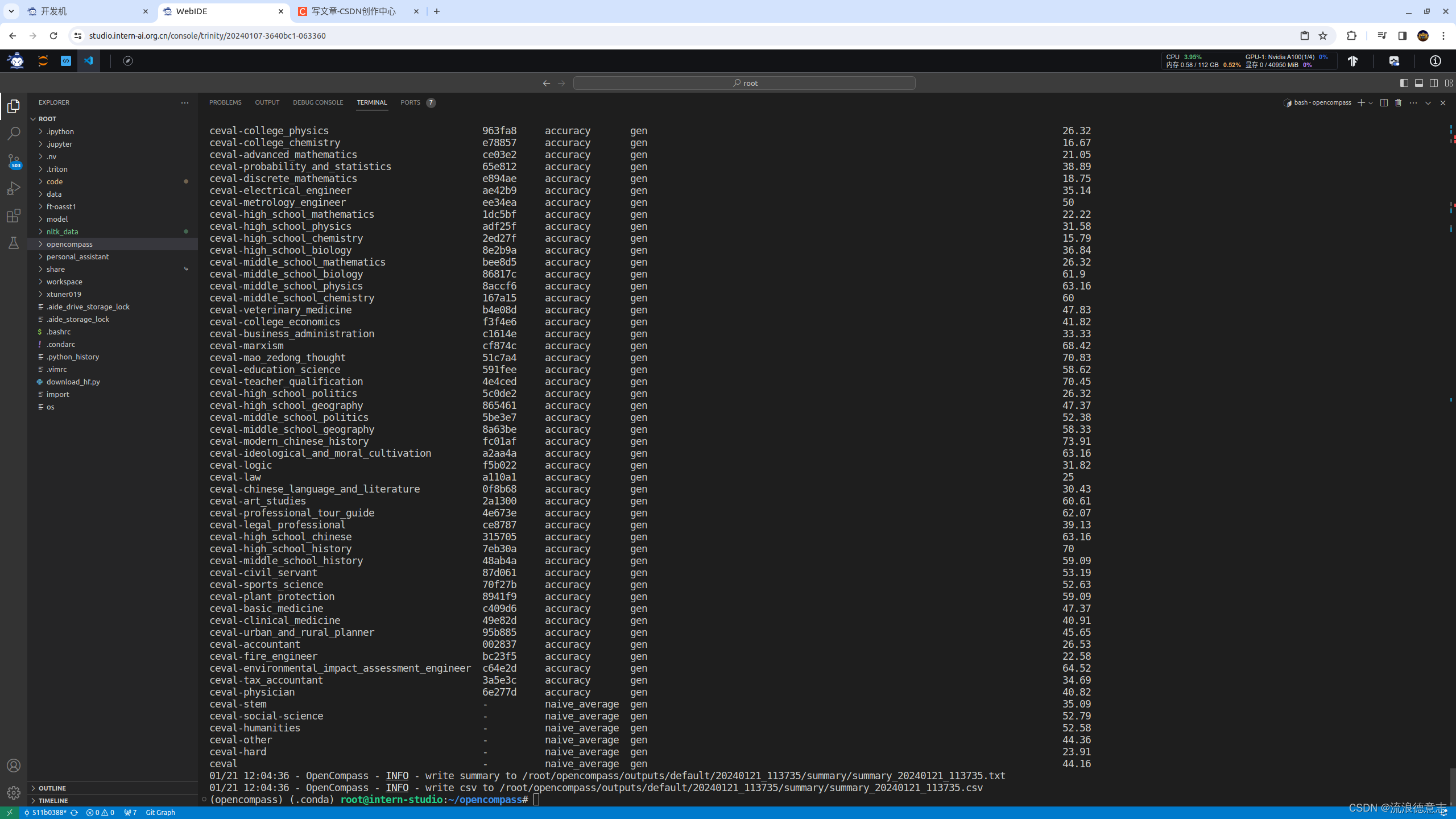
大模型实战营Day6 作业

基础作业 使用 OpenCompass 评测 InternLM2-Chat-7B 模型在 C-Eval 数据集上的性能 环境配置 conda create --name opencompass --clone/root/share/conda_envs/internlm-base source activate opencompass git clone https://github.com/open-compass/opencompass cd openco…...

编程日记 2024/1/22 4:36:24

C#，入门教程(20)——列表（List）的基础知识

上一篇&#xff1a; C#&#xff0c;入门教程(19)——循环语句&#xff08;for&#xff0c;while&#xff0c;foreach&#xff09;的基础知识https://blog.csdn.net/beijinghorn/article/details/124060844 List顾名思义就是数据列表&#xff0c;区别于数据数组&#xff08;arr…...

编程日记 2024/1/22 4:34:22

【蓝桥杯日记】复盘篇一：深入浅出顺序结构

&#x1f680;前言 本期是一篇关于顺序结构的题目的复盘,通过复盘基础知识&#xff0c;进而把基础知识学习牢固&#xff01;通过例题而进行复习基础知识。 &#x1f6a9;目录 前言 1.字符三角形 分析&#xff1a; 知识点&#xff1a; 代码如下 2. 字母转换 题目分析: 知…...

编程日记 2024/1/22 4:29:18

【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15

缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下&#xff1a; struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

编程新知 2025/11/27 21:52:13

前端导出带有合并单元格的列表

// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

编程新知 2026/1/25 3:21:09

基于数字孪生的水厂可视化平台建设：架构与实践

分享大纲&#xff1a; 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年&#xff0c;数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段&#xff0c;基于数字孪生的水厂可视化平台的…...

编程新知 2025/12/23 17:14:55

视频字幕质量评估的大规模细粒度基准

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用&#xff0c;因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型&#xff08;VLMs&#xff09;在字幕生成方面…...

编程新知 2026/2/6 9:24:15

WordPress插件：AI多语言写作与智能配图、免费AI模型、SEO文章生成

厌倦手动写WordPress文章&#xff1f;AI自动生成&#xff0c;效率提升10倍&#xff01; 支持多语言、自动配图、定时发布&#xff0c;让内容创作更轻松&#xff01; AI内容生成 → 不想每天写文章&#xff1f;AI一键生成高质量内容&#xff01;多语言支持 → 跨境电商必备&am…...

编程新知 2026/1/30 17:24:20

项目部署到Linux上时遇到的错误（Redis，MySQL，无法正确连接，地址占用问题）

Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败&#xff0c;具体原因是客户端发送了密码认证请求&#xff0c;但Redis服务器未设置密码 1.为Redis设置密码&#xff08;匹配客户端配置&#xff09; 步骤&#xff1a; 1&#xff09;.修…...

编程新知 2026/2/8 14:19:47

OPENCV形态学基础之二腐蚀

一.腐蚀的原理 (图1) 数学表达式&#xff1a;dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一&#xff0c;腐蚀跟膨胀属于反向操作&#xff0c;膨胀是把图像图像变大&#xff0c;而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

编程新知 2026/2/8 22:00:17

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”（装配）

船舶制造装配管理现状&#xff1a;装配工作依赖人工经验&#xff0c;装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书&#xff0c;但在实际执行中&#xff0c;工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

编程新知 2026/2/6 2:16:18

R语言速释制剂QBD解决方案之三

本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

编程新知 2026/2/9 2:43:24

GO协程(Goroutine)问题总结

在使用Go语言来编写代码时&#xff0c;遇到的一些问题总结一下 [参考文档]&#xff1a;https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现&#xff1a; 今天在看到这个教程的时候&#xff0c;在自己的电…...

编程新知 2026/1/31 6:53:53