【AI理论知识】EM算法
基本定义
期望最大化算法(Expectation-Maximization,EM算法)是一种用于估计包含潜在变量的概率模型参数的迭代优化算法。EM算法的主要目标是在存在未观测数据或缺失数据的情况下,通过迭代地进行期望步骤(E步)和最大化步骤(M步),来估计模型的参数。
算法步骤
-
初始化: 随机初始化模型参数。
-
E步(Expectation): 使用当前模型参数估计潜在变量的期望(Expectation)。这通常涉及计算给定观测数据的潜在变量的后验分布。
-
M步(Maximization): 最大化期望步骤中计算得到的期望,更新模型的参数。这涉及通过最大化似然函数或边缘似然函数来找到新的参数。
-
迭代: 重复执行E步和M步,直到模型参数收敛或达到预定的迭代次数。
优点
对潜在变量的处理能力和在估计复杂模型参数时的鲁棒性
缺点
其对初始值的敏感性和可能陷入局部最优解。
应用场景
-
高斯混合模型(GMM): EM算法的典型应用之一是对高斯混合模型的参数估计。GMM在许多领域中被用于建模复杂的概率分布,例如图像分割、语音识别和模式识别。
-
缺失数据问题: 当数据中存在缺失值时,EM算法可以用于估计缺失数据的概率分布。这在处理实际数据集时很常见,例如医学或社会科学研究中的调查数据。
-
混合模型: EM算法可以用于估计混合模型的参数,其中数据可以由多个组成分或成分生成。这种模型在聚类、分布拟合和异常检测等任务中有应用。
-
隐变量模型: 在一些问题中,存在未观测到的隐变量,而EM算法可以用于通过观测数据来估计这些隐变量的分布,从而推断模型的参数。
-
正态混合模型: EM算法被广泛应用于正态混合模型的参数估计,这在金融领域中用于建模资产收益率和风险管理。
-
模型选择: EM算法也可以用于模型选择问题,通过比较不同模型的似然性来确定最合适的模型。
-
概率图模型: 在概率图模型中,EM算法可以用于参数估计,例如在隐马尔可夫模型(HMM)中,用于估计转移概率和观测概率。
-
文本挖掘: EM算法在文本挖掘中被用于主题模型,如Latent Dirichlet Allocation(LDA),用于发现文本数据中的隐藏主题结构。
实例
实现医学图像去噪
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal# 生成带噪声的二维图像
np.random.seed(42)
size = 100
x, y = np.meshgrid(np.linspace(0, 1, size), np.linspace(0, 1, size))
true_image = np.sin(2 * np.pi * x) * np.cos(2 * np.pi * y)
noisy_image = true_image + np.random.normal(0, 0.1, (size, size))# EM算法去噪
def em_denoise(image, num_components, num_iterations):# 将二维图像转换为一维数组flat_image = image.flatten()# 初始化模型参数mean = np.linspace(np.min(flat_image), np.max(flat_image), num_components)covariance = np.ones(num_components)weights = np.ones(num_components) / num_componentsfor _ in range(num_iterations):# E步pdfs = np.array([weights[k] * multivariate_normal.pdf(flat_image, mean[k], covariance[k]) for k in range(num_components)])posteriors = pdfs / pdfs.sum(axis=0)# M步mean = np.dot(posteriors, flat_image) / posteriors.sum(axis=1)covariance = np.dot(posteriors, (flat_image - mean.reshape(-1, 1))**2) / posteriors.sum(axis=1)weights = posteriors.sum(axis=1) / len(flat_image)# 根据估计的参数生成去噪后的图像denoised_image = np.dot(posteriors.T, mean).reshape(image.shape)return denoised_image# 使用EM算法进行去噪
num_components = 2
num_iterations = 50
denoised_result = em_denoise(noisy_image, num_components, num_iterations)# 可视化结果
plt.figure(figsize=(12, 4))
plt.subplot(131)
plt.imshow(true_image, cmap='viridis')
plt.title('True Image')plt.subplot(132)
plt.imshow(noisy_image, cmap='viridis')
plt.title('Noisy Image')plt.subplot(133)
plt.imshow(denoised_result, cmap='viridis')
plt.title('Denoised Image')plt.show()
相关文章:

【AI理论知识】EM算法
基本定义 期望最大化算法(Expectation-Maximization,EM算法)是一种用于估计包含潜在变量的概率模型参数的迭代优化算法。EM算法的主要目标是在存在未观测数据或缺失数据的情况下,通过迭代地进行期望步骤(E步ÿ…...

03 OSPF
参考文章 1 初步认识OSPF的大致内容(第三课)-CSDN博客 2...
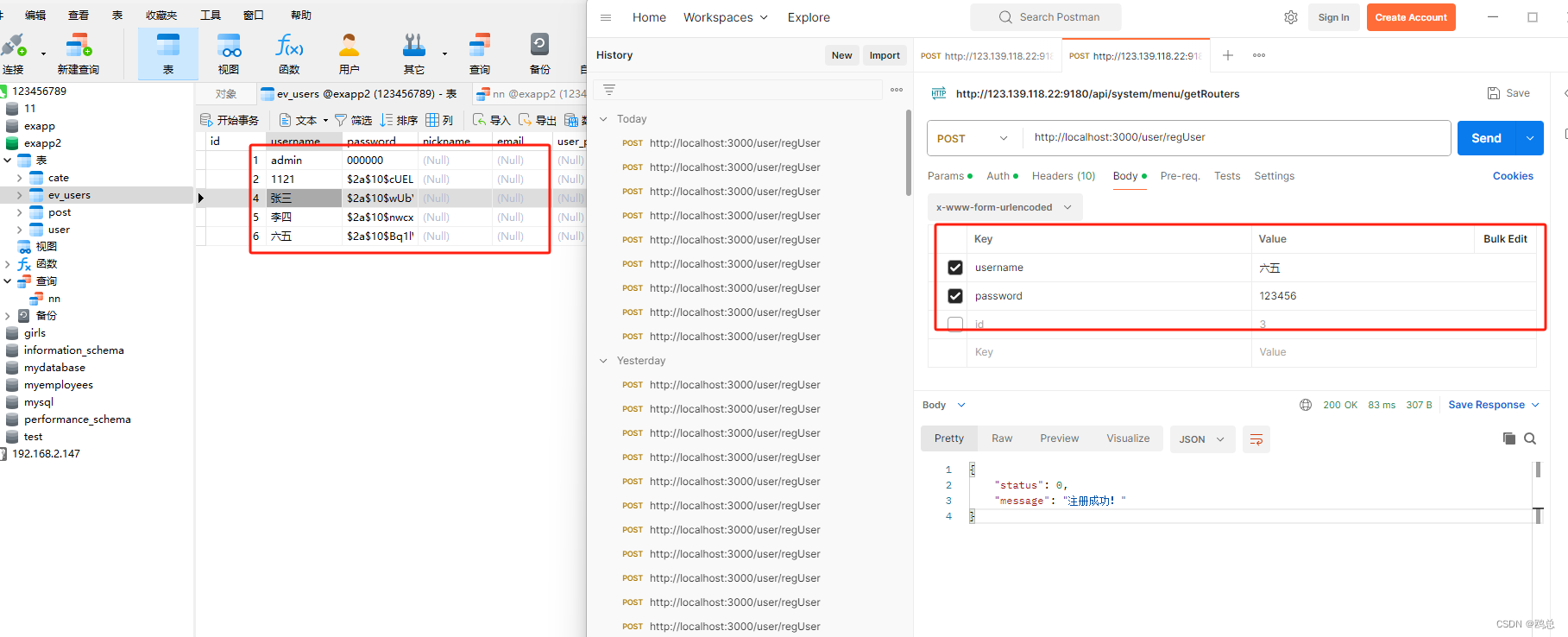
node.js(express.js)+mysql实现注册功能
文章目录 实现步骤一、获取客户端提交到服务器的用户信息,对表单中的数据,进行合法性的效验 代码如下:二、检测用户名是否被占用三、对密码进行加密四、插入新用户(完整代码)总结 实现步骤 一、获取客户端提交到服务器的用户信息…...
AI绘画Stable Diffusion进阶使用
本文讲解,模型底模,VAE美化模型,Lora模型,hypernetwork。 文本Stable Diffusion 简称sd 欢迎关注 使用模型 C站:https://civitai.com/ huggingface:https://huggingface.co/models?pipeline_tagtext-to-…...
判断)
C 练习实例33 - 质数(素数)判断
题目:判断一个数字是否为质数。 程序分析:质数(prime number)又称素数,有无限个。一个大于1的自然数,除了1和它本身外,不能被其他自然数整除。 这题做过很多遍了,懂得都懂。 代码…...
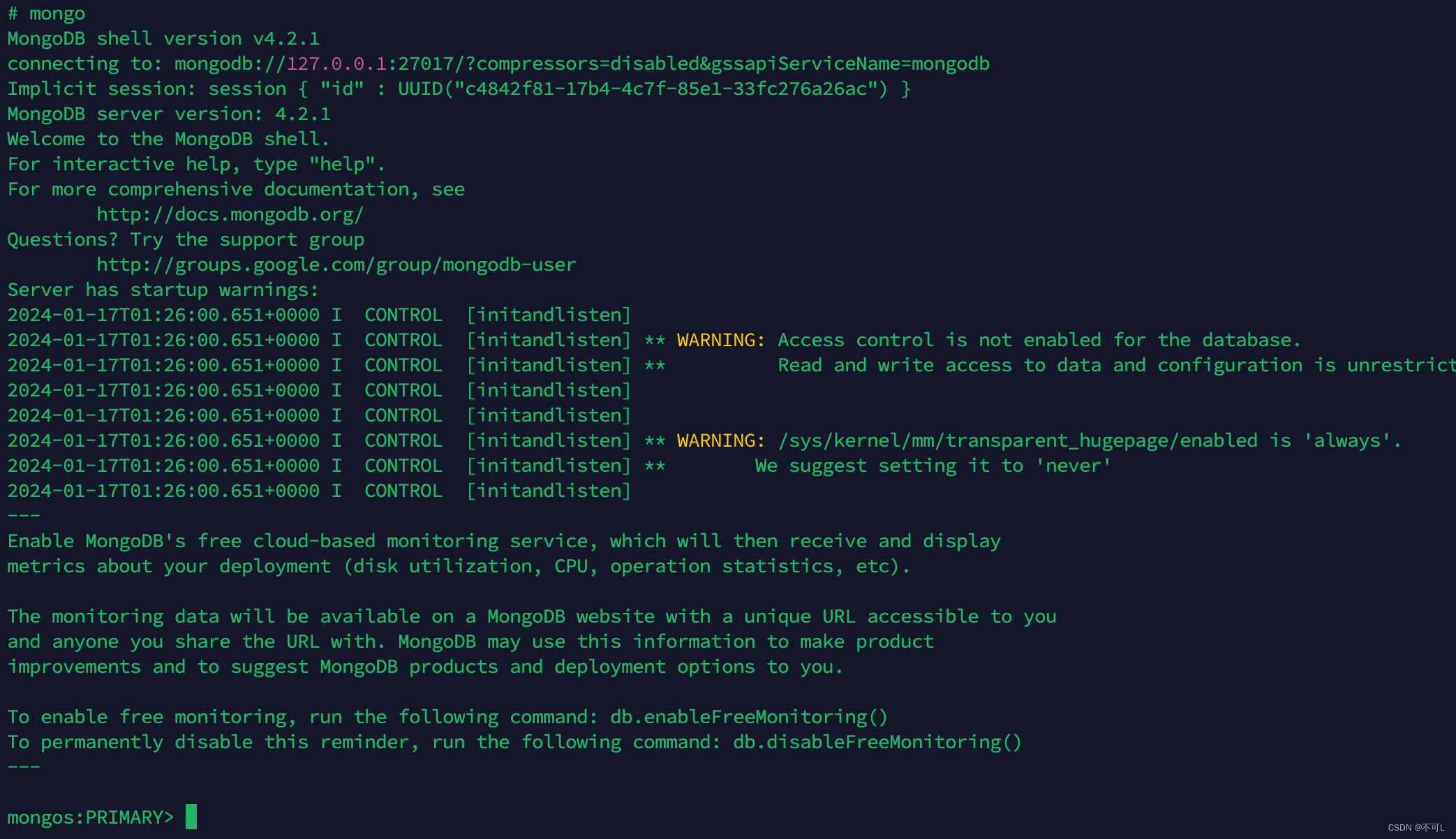
docker环境下mongo副本集的部署及异常修复
最近更换了办公地点。部署在本地docker环境里的mongo数据库不能使用了。原因是本地的ip地址变更。以前的mongo副本集的配置需要更新。处理完后,索性重新记录一下mongo副本集在docker中的部署流程。 mongo的事务及副本集 我们先了解一下什么是事务,事务…...
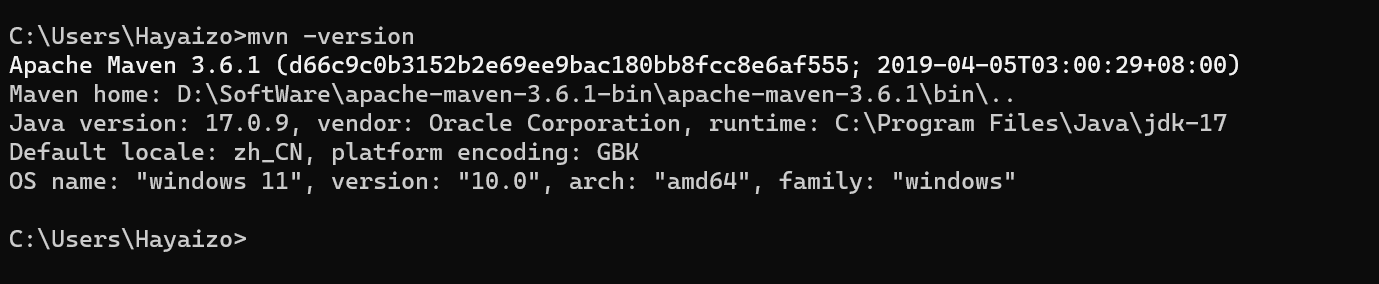
【Java】Maven的安装与配置
初识Maven Maven是专门用于管理和构建Java项目的工具,它的主要功能有: 提供了一套标准化的项目结构 提供了一套标准化的构建流程(编译,测试,打包,发布……) 提供了一套依赖管理机制 标准化的…...

向量和向量如何相乘?
向量与向量相乘主要有两种方式:点积(内积)和叉积(外积)。这两种运算的结果和应用是不同的。 点积(内积): 点积是两个向量的对应元素相乘后再求和的结果,通常用于计算两个…...
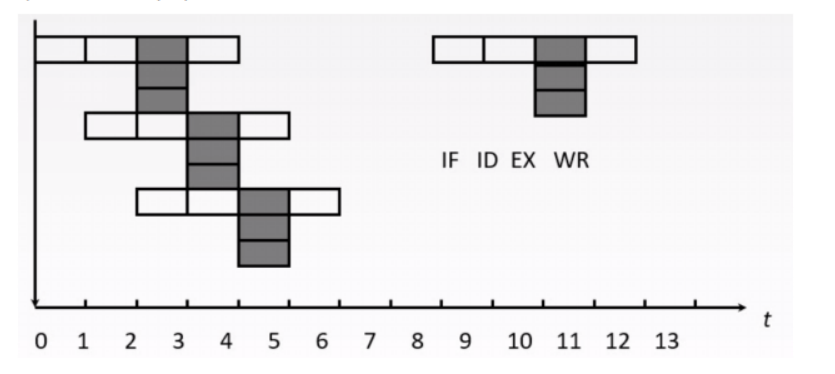
计算机组成原理 指令流水线
文章目录 指令流水线指令流水线的概念流水线性能分析流水线的吞吐率流水线的加速比流水线的效率 影响流水线的因素结构相关 (资源冲突)数据相关 (数据冲突)控制相关 (控制冲突) 流水线分类超量流水线 指令流水线 #mermaid-svg-sWaRASMFAvh8sLJk {font-family:"trebuchet m…...

macOS - md5 | md5sum
文章目录 简单使用介绍文档Linux - md5summacOS - md5 大文件传输是否完整,你可以使用 md5 进行校验 linux 上使用 md5sum 命令,在macOS 上 md5 命令是和 md5sum 等效的 简单使用介绍 参考:https://blog.csdn.net/cnds123321/article/detail…...

Tomcat快速入门
1.Tomcat介绍 Apache Tomcat 是由 Apache Software Foundation(ASF)开发的一个开源 Java WEB 应用服务器,如apache处理静态HTML能力突出不同,tomcat处理动态HTML能力相当强大,因此一般项目都是部署apachetomcat&#…...

如何结合antd design pro 5 结合express 上传多个文件
在Ant Design Pro 5(基于React)的前端界面结合Express后端实现上传整个文件夹的文件,实际上是在前端进行多文件选择,并通过POST请求将文件列表发送到后端,然后由后端处理上传。由于浏览器API限制,直接上传整…...
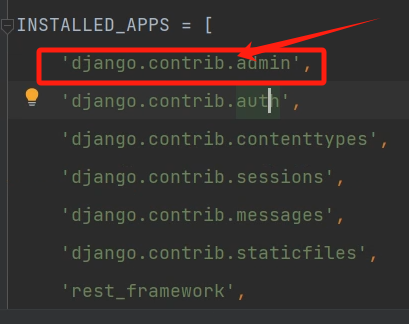
Django随笔
关于Django的admin 1. 在url中把 from django.contrib import admin 重新解开 把path(admin/,admin.site.urls), 解开 2. 注册app,在配置文件中写 django.contrib.admin, 3.输入命令进行数据库迁移 Django国际化 配置文件中(改成中文) LA…...
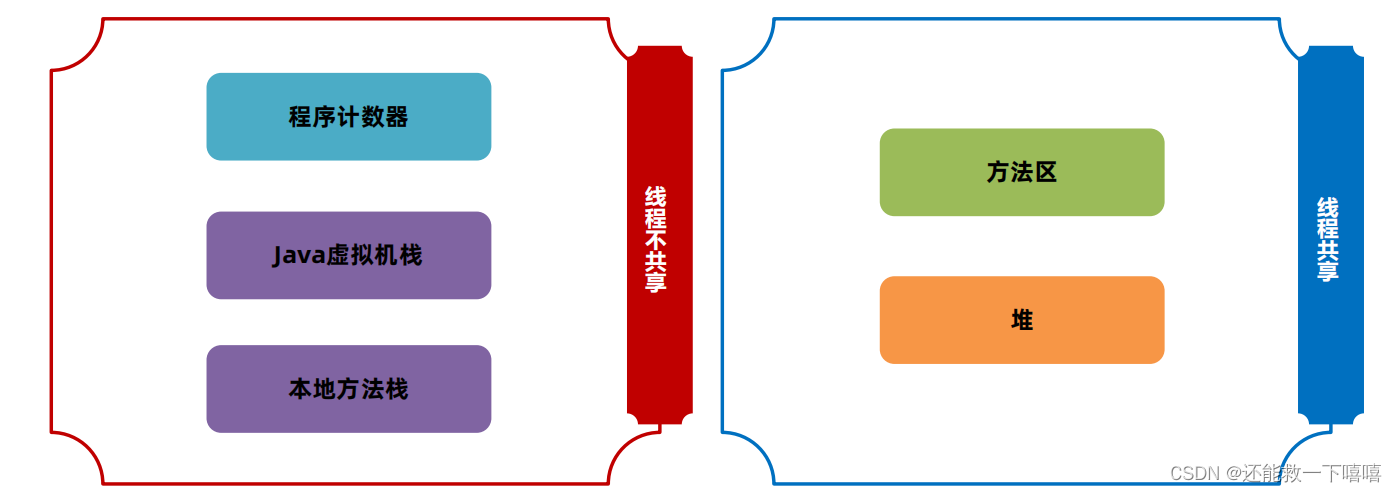
线程和进程的区别(从JVM角度出发)
进程与线程的区别 线程具有许多传统进程所具有的特征,故又称为轻型进程(Light—Weight Process)或进程元;而把传统的进程称为重型进程(Heavy—Weight Process),它相当于只有一个线程的任务。在引入了线程的操作系统中,通常一个进…...

手把手教你如何快速定位bug,如何编写测试用例,快来观摩......
手把手教你如何快速定位bug,如何编写测试用例,快来观摩......手把手教你如何快速定位bug,如何编写测试用例,快来观摩......作为一名测试人员如果连常见的系统问题都不知道如何分析,频繁将前端人员问题指派给后端人员,后端人员问题指派给前端人员…...
)
计算矩阵边缘元素之和(c++)
题目描述 输入一个整数矩阵,计算位于矩阵边缘的元素之和。所谓矩阵边缘的元素,就是第一行和最后一行的元素以及第一列和最后一列的元素。 输入格式 第一行分别为矩阵的行数 和列数 (m<100,n<100),…...
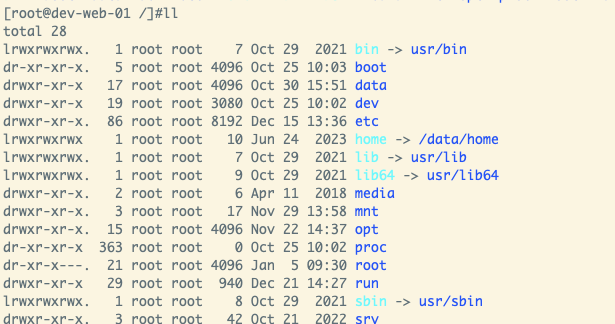
java使用jsch处理软链接判断是否文件夹
前言 这一次主要是碰到一个问题。因为使用jsch去读取文件的时候,有一些文件它是使用软链接制作的一个映射。因为这里面有一个问题。如果它是软链接你就无法判断他到底是文件。还是文件夹?因为他没有提供可以直接读取的方法,用权限信息去判断…...
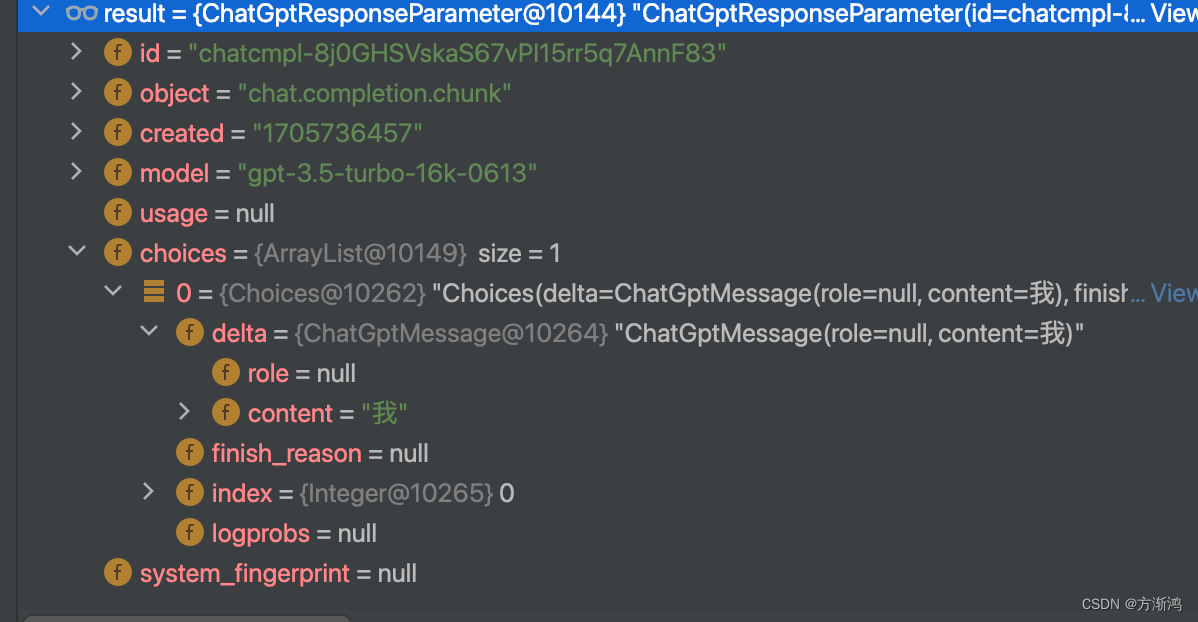
【2023】java使用WebClient实现chatGPT调用建立web socket连接
💻目录 一、介绍1、使用技术2、效果 二、代码1、前端代码2、后端代码2.1、maven依赖2.2、model2.2.1、请求接口的格式2.2.2、响应数据对象 2.3、工具类2.3.1、🔴使用WebClient调用chatgpt方法2.3.2、🟠 webSocket连接对话方法 2.4、Controlle…...
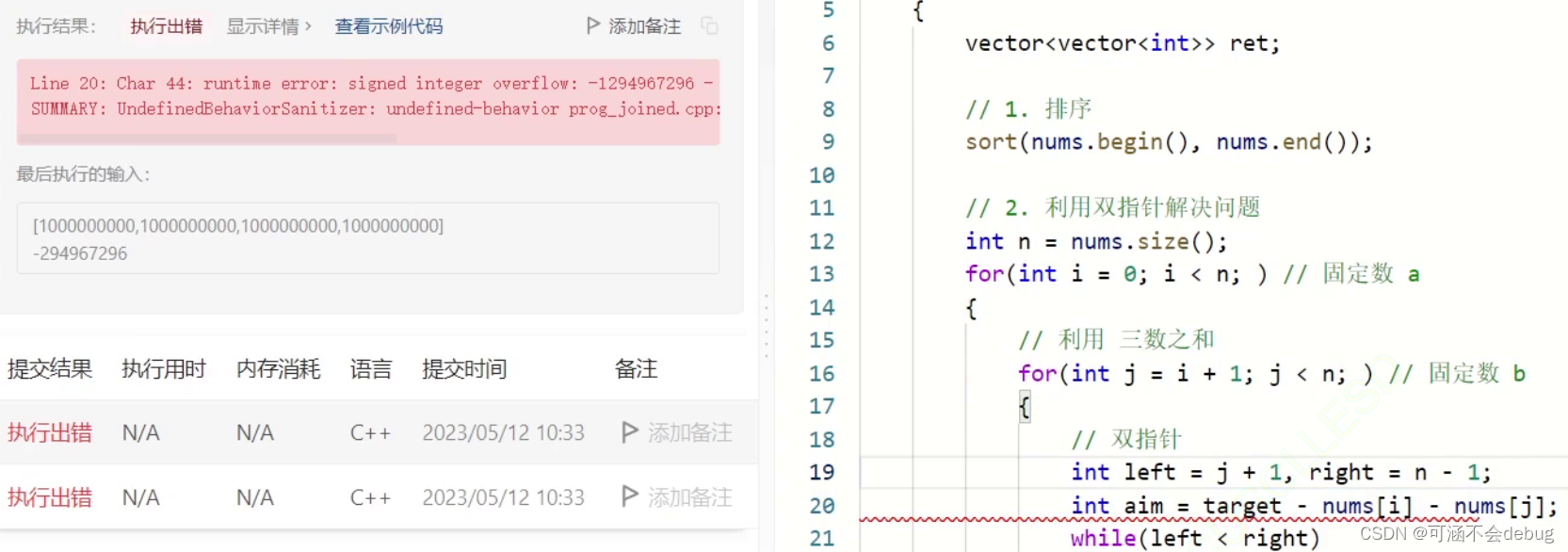
力扣【四数之和】
一、题目描述 18. 四数之和 给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复&#x…...
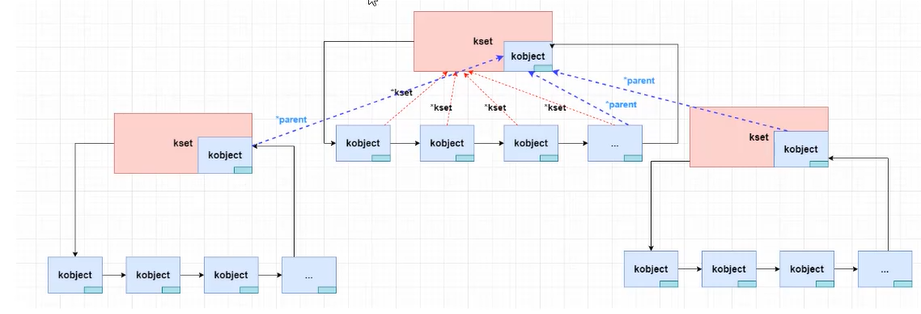
IMX6LL|linux设备驱动模型
linux设备驱动模型 为什么需要设备驱动模型 早期内核(2.4之前)没有统一的设备驱动模型,但照样可以用2.4~2.6期间使用devfs,挂载在/dev目录。 需要在内核驱动中创建设备文件(devfs_register),命名死板 2.6以后使用sys…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...
