人工智能数学验证工具LEAN4【入门介绍3】乘法世界-证明乘法的所有运算律
视频链接,创作不易记得投币哦:
import Game.Levels.Multiplication.L08add_mul
World "Multiplication"
Level 9
Title "mul_assoc"
namespace MyNat
Introduction
"
We now have enough to prove that multiplication is associative,
the boss level of multiplication world. Good luck!
"
LemmaDoc MyNat.mul_assoc as "mul_assoc" in "*" "
`mul_assoc a b c` is a proof that `(a * b) * c = a * (b * c)`.
Note that when Lean says `a * b * c` it means `(a * b) * c`.
Note that `(a * b) * c = a * (b * c)` cannot be proved by \"pure thought\":
for example subtraction is not associative, as `(6 - 2) - 1` is not
equal to `6 - (2 - 1)`.
"
/-- Multiplication is associative.
In other words, for all natural numbers $a$, $b$ and $c$, we have
$(ab)c = a(bc)$. -/
Statement mul_assoc
(a b c : ℕ) : (a * b) * c = a * (b * c) := by
induction c with d hd
· rw [mul_zero, mul_zero, mul_zero]
rfl
· rw [mul_succ]
rw [mul_succ]
rw [hd]
rw [mul_add]
rfl
LemmaTab "*"
Conclusion "
A passing mathematician notes that you've proved
that the natural numbers are a commutative semiring.
If you want to begin your journey to the final boss, head for Power World.
"
相关文章:

人工智能数学验证工具LEAN4【入门介绍3】乘法世界-证明乘法的所有运算律
视频链接,创作不易记得投币哦: import Game.Levels.Multiplication.L08add_mul World "Multiplication" Level 9 Title "mul_assoc" namespace MyNat Introduction " We now have enough to prove that multiplication is a…...

Armv8-M的TrustZone技术简介
TrustZone技术是适用于Armv8-M的可选安全扩展,旨在为各种嵌入式应用提供改进的系统安全基础。 TrustZone技术的概念并不新鲜。该技术已经在Arm Cortex-A系列处理器上使用了几年,现在已经扩展到Armv8-M处理器。 在high level上,TrustZone技术适用于Armv8-M的概念与Arm Cort…...

ctfshow-反序列化(web267-web270)
目录 web267 web268 web269 web270 总结 web267 页面用的什么框架不知道 看源码看一下 框架就是一种软件工具,它提供了一些基础功能和规范,可以帮助开发者更快地构建应用程序。比如Yii框架和ThinkPHP框架就是两个流行的PHP框架,它们提供…...
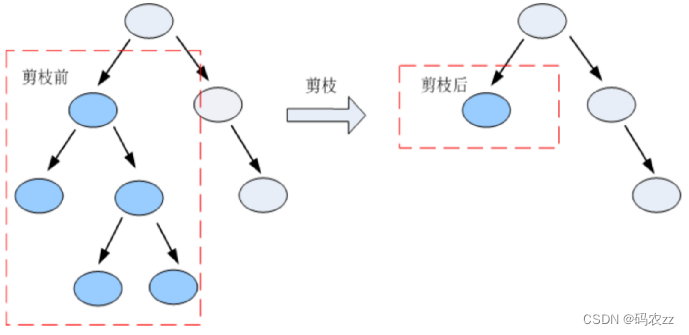
决策树的分类
概念 决策树是一种树形结构 树中每个内部节点表示一个特征上的判断,每个分支代表一个判断结果的输出,每个叶子节点代表一种分类结果 决策树的建立过程 1.特征选择:选取有较强分类能力的特征。 2.决策树生成:根据选择的特征生…...

LateX--插入伪代码类型详解
文章目录 1.算法伪代码流程图----循环带范围1.1.算法伪代码示例图11.2.算法伪代码示例图2 2.算法伪代码流程图----循环不带范围3.算法伪代码流程图---不带行数数字4.参考文献 1.算法伪代码流程图----循环带范围 #需要插入这个宏包 \usepackage[ruled,linesnumbered]{algorithm…...

《Python数据分析技术栈》第06章使用 Pandas 准备数据 04 DataFrames
04 DataFrames 《Python数据分析技术栈》第06章使用 Pandas 准备数据 04 DataFrames A DataFrame is an extension of a Series. It is a two-dimensional data structure for storing data. While the Series object contains two components - a set of values, and index …...
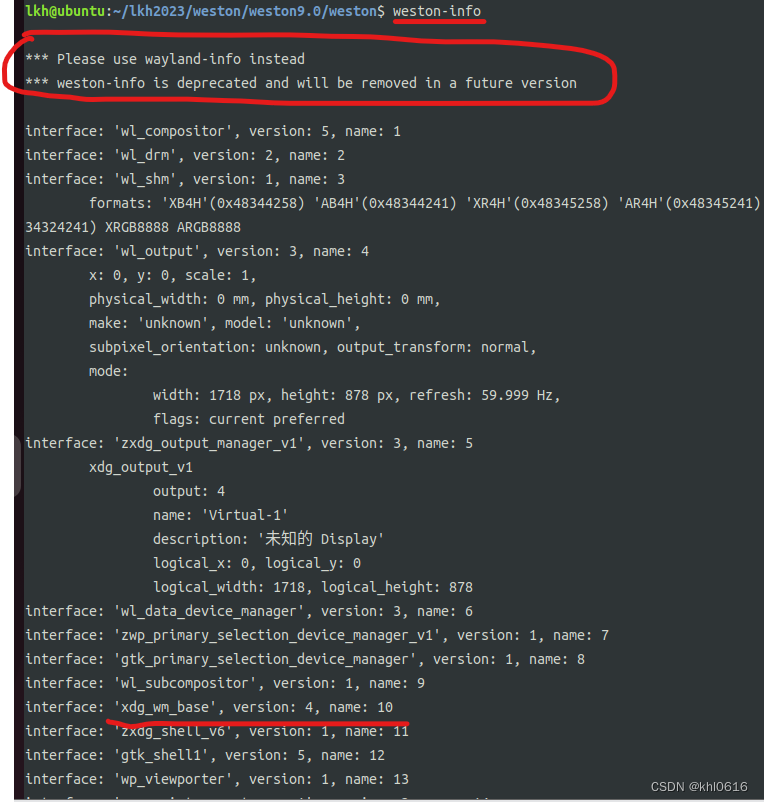
wayland(xdg_wm_base) + egl + opengles 最简实例
文章目录 前言一、ubuntu 下相关环境准备1. 获取 xdg_wm_base 依赖的相关文件2. 查看 ubuntu 上安装的opengles 版本3. 查看 weston 所支持的 窗口shell 接口种类二、xdg_wm_base 介绍三、egl_wayland_demo1.egl_wayland_demo2_0.c2.egl_wayland_demo3_0.c3. xdg-shell-protoco…...

MySQL部署
1、卸载mariadb rpm -qi mariadb-libs yum remove mysql-libs -y 2、查看操作系统内核版本及硬件架构 uname -a 3、查看glibc版本 ldd --version 4、下载mysql压缩包 wget https://cdn.mysql.com/archives/mysql-8.0/mysql-8.0.35-linux-glibc2.17-x86_64.tar 5、解压到/mnt目录…...

【ARM 嵌入式 编译系列 3.7 -- newlib 库文件与存根函数 stubs 详细介绍】
请阅读【嵌入式开发学习必备专栏 之 ARM GCC 编译专栏】 文章目录 newlib 库文件介绍资源使用平台支持功能性能许可证兼容性系统调用函数介绍系统调用存根 stubs 详细介绍为什么需要系统调用存根(Stubs)?常见的系统调用存根如何实现系统调用存根如何告知编译器使用自定义存根…...

【C++】结构体
目录 1.结构体基本概念 2.结构体的定义和使用 3.结构体数组 4.结构体指针 5.结构体嵌套结构体 6.结构体做函数参数 7.结构体中const使用场景 1.结构体基本概念 结构体属于用户 ---- 自定义的数据类型,允许用户储存不同的数据类型 2.结构体的定义和使用 语法…...

web架构师编辑器内容-拖动元素改变元素的位置和大小的完成
拖动移动元素 改变编辑器的定位系统 我们目前的元素都是按照块级元素直接自上而下的排列在画布中,为了让元素实现精确的定位和调整,我们需要改变这些元素的定位实现。我们需要让这些元素画布区域来进行绝对定位。如果我们有一个元素有这些已经保存的 c…...
基于CNN的水果识别-含数据集训练模型
数据集介绍,下载本资源后,界面如下: 有一个文件夹一个是存放数据集的文件。 数据集介绍: 一共含有:8个类别,包含:Apple, Banana, Cherry, Dragon Fruit, Mango, Orange, Papaya, Pineapple等。 然后本地的train.txt和…...
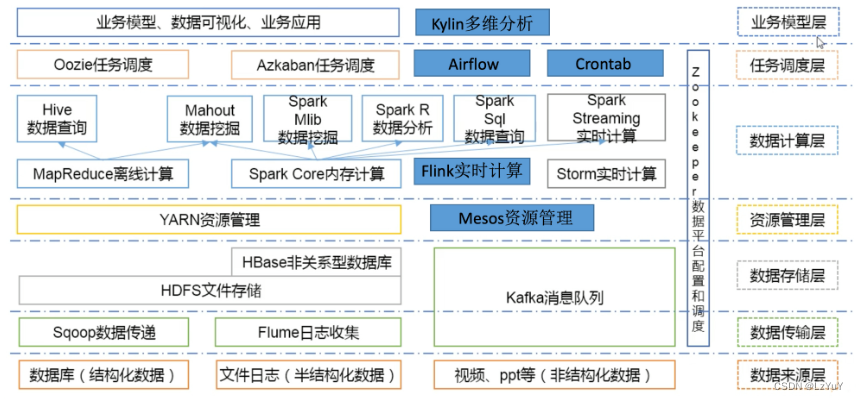
Hadoop基本概论
目录 一、大数据概论 1.大数据的概念 2.大数据的特点 3.大数据应用场景 二、Hadoop概述 1.Hadoop定义 2.Hadoop发展历史 3.Hadoop发行版本 4.Hadoop优势 5.Hadoop1.x/2.x/3.x 6.HDFS架构 7.Yarn架构 8.MapReduce架构 9.大数据技术生态体系 一、大数据概论 1.大数…...
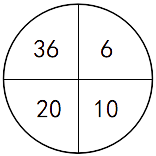
2023年12月 Scratch 图形化(一级)真题解析#中国电子学会#全国青少年软件编程等级考试
Scratch图形化等级考试(1~4级)全部真题・点这里 一、单选题(共25题,每题2分,共50分) 第1题 观察下列每个圆形中的四个数,找出规律,在括号里填上适当的数?( ) A:9 B:17 C:21 D:5 答案:C 左上角的数=下面两个数的和+右上角的数...
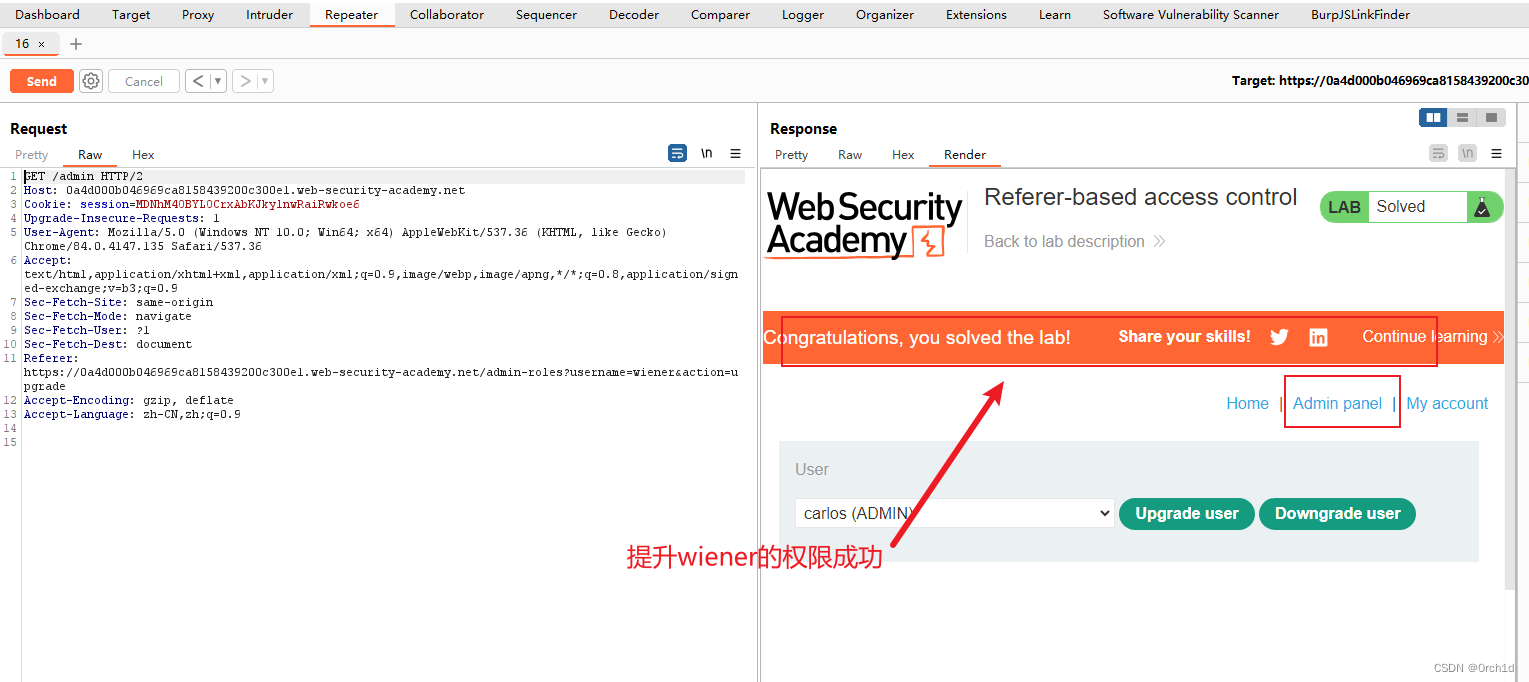
burp靶场--访问控制【越权】
【Burp系列】超全越权漏洞实验总结 https://portswigger.net/web-security/access-control/lab-unprotected-admin-functionality 1. 访问控制【越权】 https://portswigger.net/web-security/access-control#what-is-access-control ### 什么是访问控制: 访问控…...

C#使用DateTime.Now静态属性动态获得系统当前日期和时间
目录 一、实例 1.源码 2.生成效果 二、相关知识点 1.Thread类 (1)Thread.Sleep()方法 (2)Thread(ThreadStart) (3)IsBackground (4)Invoke( ) 2.CreateGrap…...

华为机考入门python3--(0)模拟题2-vowel元音字母翻译
分类:字符串 知识点: 字符串转list,每个字符成为list中的一个元素 list(string) 字符串变大小写 str.upper(), str.lower() 题目来自【华为招聘模拟考试】 # If you need to import additional packages or classes, please import …...

【轮式平衡机器人】——角度/速度/方向控制分析软件控制框架
轮式平衡机器人具有自不稳定性,可类比一级倒立摆系统的控制方法,常见有反馈线性化方法、非线性PID控制、自适应控制、自抗扰控制,还有改进的传统缺乏对外界干扰和参数改变鲁棒性的滑模变结构控制。我们采用较为简单的双闭环PID控制实现平衡模…...
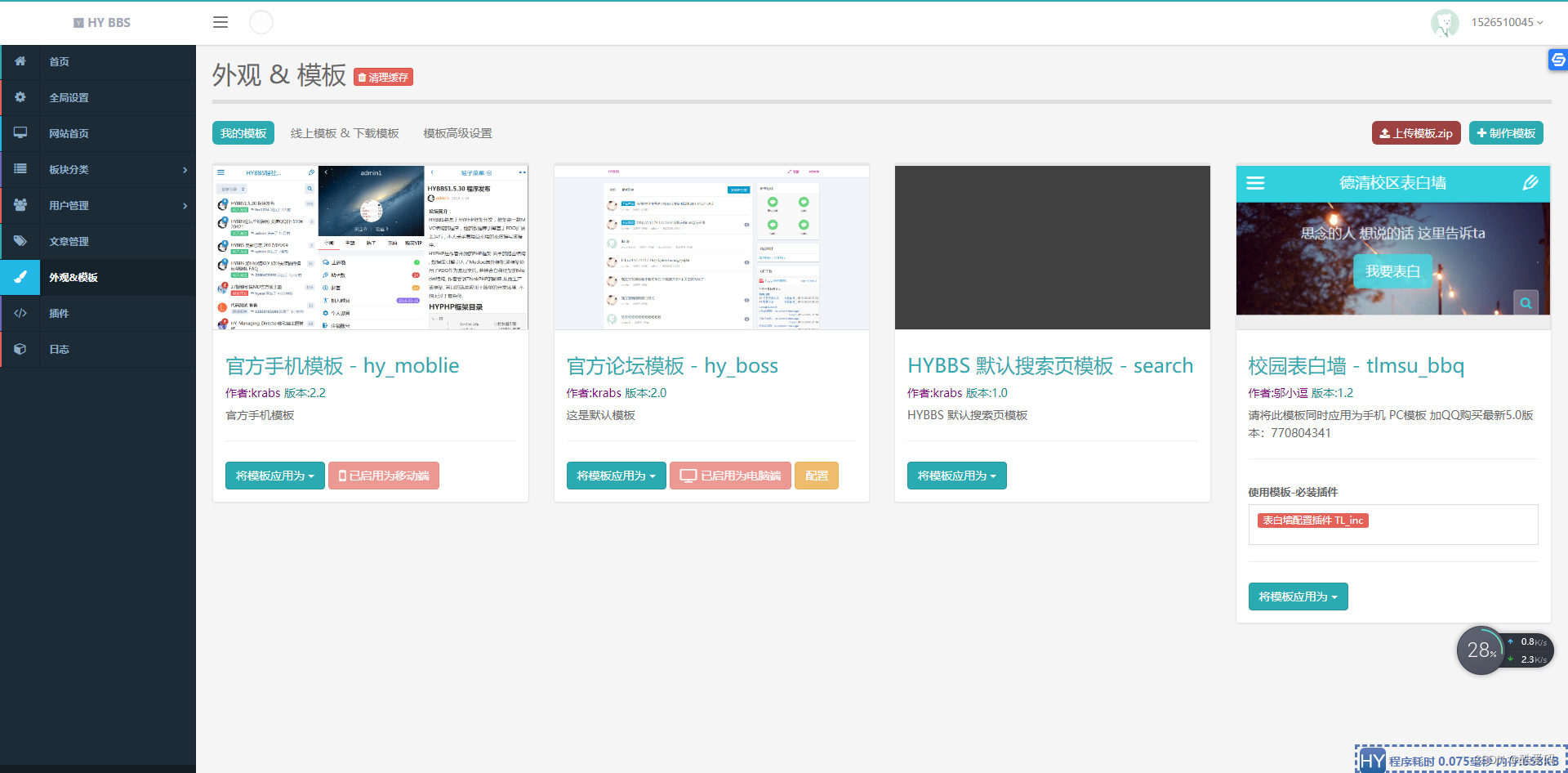
HYBBS 表白墙网站PHP程序源码 可封装成APP
源码介绍 PHP表白墙网站源码,可以做校园内的,也可以做校区间的,可封装成APP。告别QQ空间的表白墙吧。 安装PHP5.6以上随意 上传程序安装,然后设置账号密码,登陆后台切换模板手机PC都要换开启插件访问前台。 安装完…...
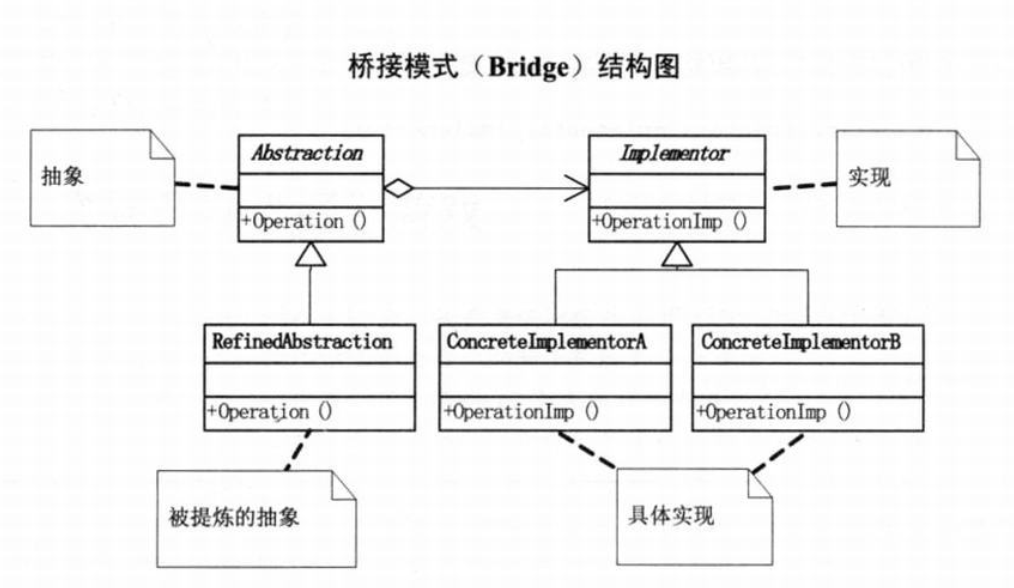
【设计模式】适配器和桥接器模式有什么区别?
今天我探讨一下适配器模式和桥接模式,这两种模式往往容易被混淆,我们希望通过比较他们的区别和联系,能够让大家有更清晰的认识。 适配器模式:连接不兼容接口 当你有一个类的接口不兼容你的系统,而你又不希望修改这个…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
