AtCoder Regular Contest 170(A~B)
A - Yet Another AB Problem
给你两个字符串S和T,你可以对S执行操作,选择两个字符,将前面的改为A,后面的改为B,最少操作几次可以把S改成T。如果改不成就输出-1。
从左往右一个一个改过去,分类讨论,如果是要把A改成B。
S:A->B
T:B
那么T中该位置前面一定要有一个A,否则无法修改。
如果要把B改成A。
S:B->A
T:A
那么T中该位置后面一定要有一个B,否则无法修改。
其中可以本次修改可以更优,即S中后面有一个A,对应T后面的B(一次修改,完成两次对应)
#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define fr first
#define se second
#define endl '\n'
using namespace std;
const int N=2e5+5;int n,ans,a;
string s,t;queue<int>q;
int b[N];void solve(){cin>>n>>s>>t;per(i,0,n-1){if(t[i]=='B' and s[i]=='A')q.push(i);}rep(i,n-1,0){if(t[i]=='B')b[i]++;if(i>=1)b[i-1]=b[i];}per(i,0,n-1){if(t[i]=='A')a++;if(s[i]!=t[i]){if(s[i]=='A'){//需要改成B,前面至少有一个Aif(!a){cout<<-1<<endl;return ;}ans++;}else{//需要改成A,后面至少有一个Bif(!b[i+1]){cout<<-1<<endl;return;}ans++;while(!q.empty() and q.front()<i)q.pop();if(!q.empty()){s[q.front()]='B';q.pop();}}}}cout<<ans<<endl;
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}补题:B - Arithmetic Progression Subsequence
给你1e5个数,每个数是1~10。对于l和r区间,如果区间中有三个数(不管顺序)a[j],a[k],a[l],满足1 2 3或3 2 1(差为1) 或者1 5 9,9 5 1(差为4)这种差相等的,说明l和r是一个好区间,号区间有几个。
思路1:考虑差值最大只有可能是4,对于一个数a[i],只需要枚举所有差值(sub:1~4),a[i],a[i]+sub,a[i]+2*sub(注意也可以是减法),如果在a[i]之后存在这样的值,那么第三个数的下标及其以后都是好区间。所以只需要想一个算法维护每个数后面的1~10第一次出现的位置。
思路2:找到一个好区间之后就可以无限左右扩展,还需要去判断内部是否有好空间,如果内部有一个好空间,那么外部也都是好空间,所以不应该是从每一个数开始枚举,应该枚举好空间序列长度,从3开始往上扩展。
正确思路:正难则反,只会出现1~10的数,尝试构建无解的情况,从差为0开始往上,如果差重复了就必然有解,如1 1 2 4 8,几乎就没别的数可以填了,就会开始重复了。
AC代码
#include <bits/stdc++.h>
#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define fr first
#define se second
#define endl '\n'
using namespace std;
const int N=1e5+5;int n,a[N],ans;bool check(int l,int r){//约1~100次查询per(i,l,r){per(j,i+1,r){per(k,j+1,r){if(a[j]-a[i]==a[k]-a[j])return true;}}}return false;
}void solve(){cin>>n;per(i,1,n)cin>>a[i];per(i,1,n){per(j,i+1,n){//i和j差到10以内就必然有解,复杂度是带系数的O(n),check比较烂总体约1e9if(check(i,j)){ans+=n-j+1;break;}}}cout<<ans<<endl;
}signed main(){ios::sync_with_stdio(false),cin.tie(nullptr);int t=1;while(t--)solve();return 0;
}顺带一提不开long long见祖宗。

相关文章:

AtCoder Regular Contest 170(A~B)
A - Yet Another AB Problem 给你两个字符串S和T,你可以对S执行操作,选择两个字符,将前面的改为A,后面的改为B,最少操作几次可以把S改成T。如果改不成就输出-1。 从左往右一个一个改过去,分类讨论&#x…...

rk1126, 实现 yolov8 目标检测
基于 RKNN 1126 实现 yolov8 目标检测 Ⓜ️ RKNN 模型转换 ONNX yolo export model./weights/yolov8s.pt formatonnx导出 RKNN 这里选择输出 concat 输入两个节点 onnx::Concat_425 和 onnx::Concat_426 from rknn.api import RKNNONNX_MODEL ./weights/yolov8s.onnxRKNN_MOD…...

【软件测试】学习笔记-网站可扩展性架构设计
可扩展性,指的是网站的架构设计能够快速适应需求的变化,当需要增加新的功能实现时,对原有架构不需要做修改或者做很少的修改就能够快速实现新的业务需求。 从这个定义中,我们很容易就可以得出衡量网站可扩展性设计优秀与否的主要标…...
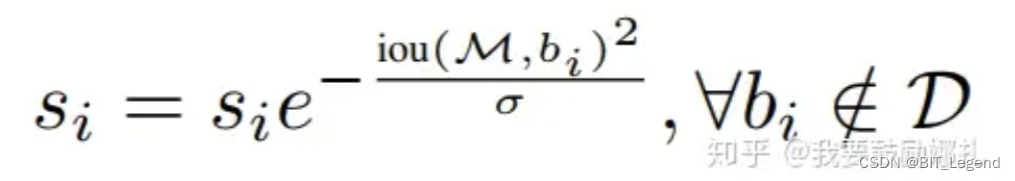
深度学习常用代码总结(k-means, NMS)
目录 一、k-means 算法 二、NMS 一、k-means 算法 k-means 是一种无监督聚类算法,常用的聚类算法还有 DBSCAN。k-means 由于其原理简单,可解释强,实现方便,收敛速度快,在数据挖掘、数据分析、异常检测、模式识别、金…...
数据结构·顺序表应用
本节应用是要用顺序表实现一个通讯录,收录联系人的姓名、性别、电话号码、住址、年龄 顺序表的实现在上一节中已经完成了,本节的任务其实就是应用上节写出来的代码的那些接口函数功能,做出来一个好看的,可…...

第一个 OpenGL 程序:旋转的立方体(VS2022 / MFC)
文章目录 OpenGL API开发环境在 MFC 中使用 OpenGL初始化 OpenGL绘制图形重置视口大小 创建 MFC 对话框项目添加 OpenGL 头文件和库文件初始化 OpenGL画一个正方形OpenGL 坐标系改变默认颜色 重置视口大小绘制立方体使用箭头按键旋转立方体深度测试添加纹理应用纹理换一个纹理 …...

剩余银饰的重量 - 华为OD统一考试
OD统一考试(C卷) 分值: 100分 题解: Java / Python / C 题目描述 有N块二手市场收集的银饰,每块银饰的重量都是正整数,收集到的银饰会被熔化用于打造新的饰品。 每一回合,从中选出三块 最重的…...
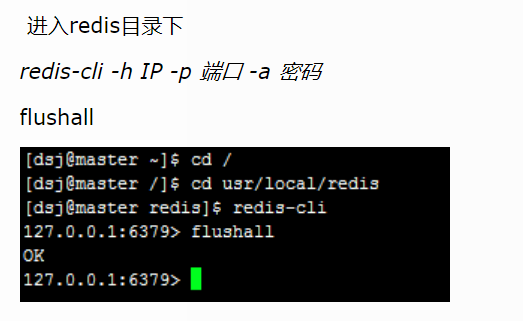
redis远程连接不上解决办法
问题描述: redis远程服务端运行在192.168.3.90计算机上,客户端计算机(ip:192.168.3.110)通过redsi-cli.exe客户端工具连接时,没有反应,连接不上。 如图所示: 解决步骤: 步骤一&…...
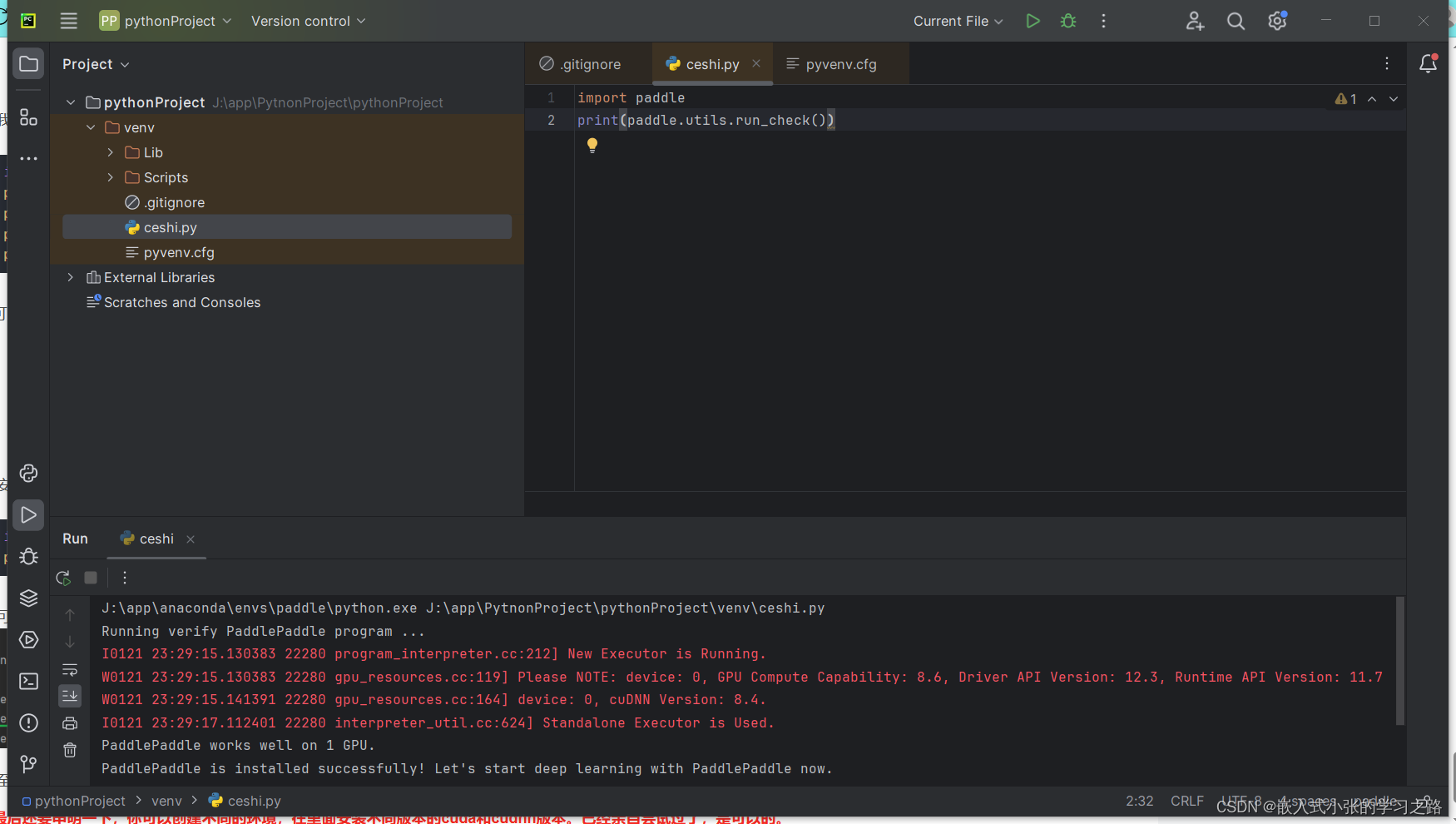
利用Anaconda安装pytorch和paddle深度学习环境+pycharm安装后不能调用pytorch和paddlepaddle框架
问题现象: 之前安装后不能在添加pytorch和paddlepaddle框架 原因(疑似): 在终端中显示pytorch和paddle在C盘但是安装是安装在J盘 解决办法: 卸载、删除文件重新安装后可以看到文件位置在J盘中 但是选择时还是显示C…...
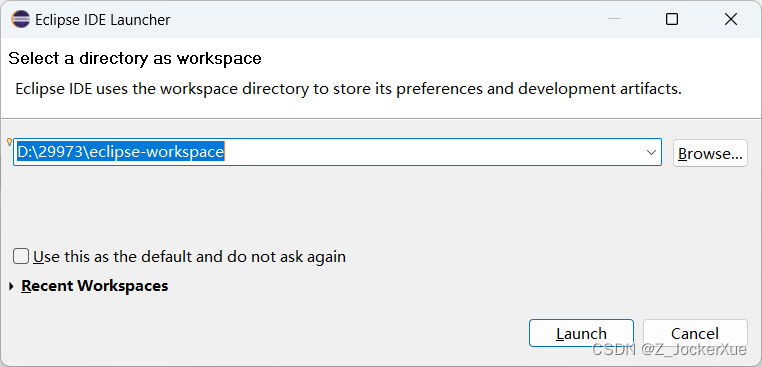
Eclipses安装教程
一、下载开发工具包 1、开发工具包JDK 下载地址链接:https://www.oracle.com/cn/java/technologies/downloads/ 下载教程: 1)点击链接,可以跳转到页面 2)下滑页面,找到开发工具包 3) 记住下载之…...

安装python版opencv的一些问题
安装python版opencv的一些问题 OpenCV是知名的开源计算机视觉算法库,提供了C\Python\Java版共享库。 在Python中使用OpenCV格外简单,一句命令就能安装,一行import就能引入,可谓是神器。然而,在实际使用中可能遇到一些…...
RabbitMQ入门实战
RabbitMQ 是一个开源的消息中间件,实现了高级消息队列协议(AMQP),用于在分布式系统中进行消息传递。它能够在应用之间传递消息,解耦应用组件,提高系统的可伸缩性和可维护性。RabbitMQ 使用高级消息队列协议…...
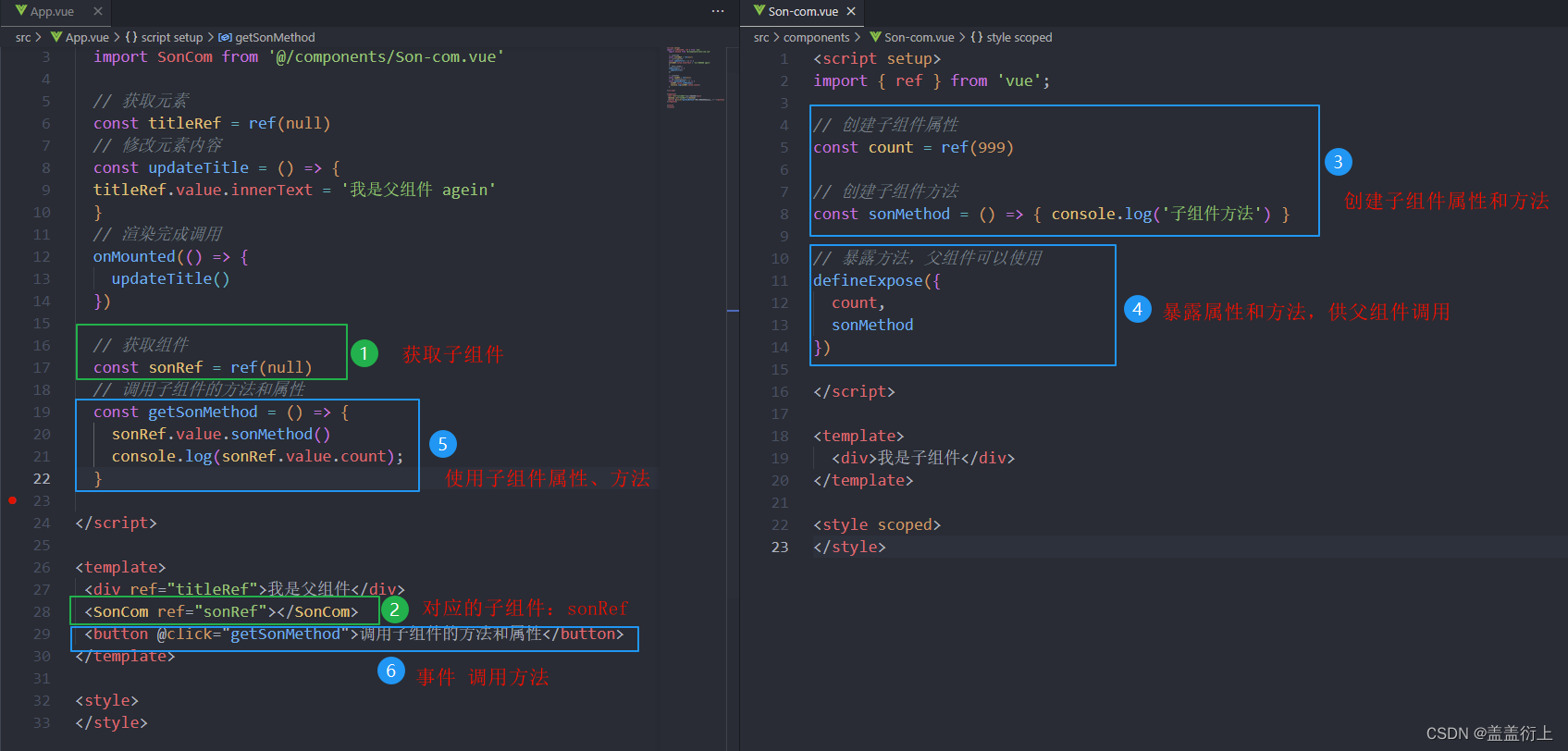
vue3-模版引用ref
1. 介绍 概念:通过 ref标识 获取真实的 dom对象或者组件实例对象 2. 基本使用 实现步骤: 调用ref函数生成一个ref对象 通过ref标识绑定ref对象到标签 代码如下: 父组件: <script setup> import { onMounted, ref } …...

C# 十大排序算法
以下是常见的十大排序算法(按照学习和实现的顺序排列): 冒泡排序(Bubble Sort)选择排序(Selection Sort)插入排序(Insertion Sort)希尔排序(Shell Sort&…...
面试之Glide如何绑定Activity的生命周期
Glide绑定Activity生命周期 Glide.with() 下面都是它的重载方法,Context,Activity,FragmentActivity, Fragment, android.app.Fragment fragment,View都可以作为他的参数,内容大同小异,都是先getRetriever࿰…...

从 fatal 错误到 sync.Map:Go中 Map 的并发策略
为什么 Go 语言在多个 goroutine 同时访问和修改同一个 map 时,会报出 fatal 错误而不是 panic?我们该如何应对 map 的数据竞争问题呢? 这篇文章将带你一步步了解背后的原理,并引出解决 map 并发问题的方案。 Map 数据竞争 首先…...

Simon算法详解
0.0 Intro 相关的算法: Deutsh-Jozsa算法: 第一个量子算法对经典算法取得指数级加速的算法 美中不足在于只能确定函数是平衡的还是非平衡的,无法确定函数具体的内容,即无法直接解出函数 Bernstein-Vazirani算法ÿ…...

jrebel IDEA 热部署
1 下载 2022.4.1 JRebel and XRebel - IntelliJ IDEs Plugin | Marketplace 2 选择下载好的zip 离线安装IDEA 插件 重启IDEA 3 打开 [Preference -> JRebel & XRebel] 菜单,输入 GUID address 为 https://jrebel.qekang.com/1e67ec1b-122f-4708-87d…...

pdf拆分成各个小pdf的方法
背景:由于某些缘故,一个大的pdf需要拆分成页数少的pdf,或者pdf需要去掉指定页,那么就有必要对pdf进行重新编辑,这里需要用到一个库,直接进行操作即可。 当使用Python时,可以使用PyMuPDF库来拆分PDF文件。以下是一个示例代码, import fitz # PyMuPDF def split_pdf(i…...

IntelliJ IDEA 常用快捷键一览表(通用型,提高编写速度,类结构、查找和查看源码,替换与关闭,调整格式)
文章目录 IntelliJ IDEA 常用快捷键一览表1-IDEA的日常快捷键第1组:通用型第2组:提高编写速度(上)第3组:提高编写速度(下)第4组:类结构、查找和查看源码第5组:查找、替换…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
