八大排序算法之堆排序的实现+经典TopK问题
目录
一.堆元素的上下调整接口
1.前言
2.堆元素向上调整算法接口
3.堆元素向下调整算法接口
二.堆排序的实现
1.空间复杂度为O(N)的堆排序(以排升序为例)
思路分析:
代码实现:
排序测试:
时空复杂度分析:
2. 空间复杂度为O(1)的堆排序(以排降序为例)
将数组arr调整成堆的思路:
将数组arr调整成堆的时间复杂度分析:
在数组arr数组被调整成堆的基础上完成排序的思路
堆排序代码实现:
排序时空复杂度分析:
三.用堆数据结构解决TopK问题
1. 问题描述:
2.问题分析与求解
一.堆元素的上下调整接口
1.前言
完全二叉树的物理结构和逻辑结构:
关于堆和堆元素上下调整算法接口的设计原理分析参见青菜的博客http://t.csdn.cn/MKzyt
http://t.csdn.cn/MKzyt青菜友情提示:想要深刻理解堆排序,必须掌握堆的构建
注意:接下来给出的两个接口是针对小根堆的元素调整算法接口,若需要用到大根堆数据结构,只需在小根堆的元素调整算法接口中将子父结点值比较符号换一下方向即可用于实现大根堆.
2.堆元素向上调整算法接口
函数首部:
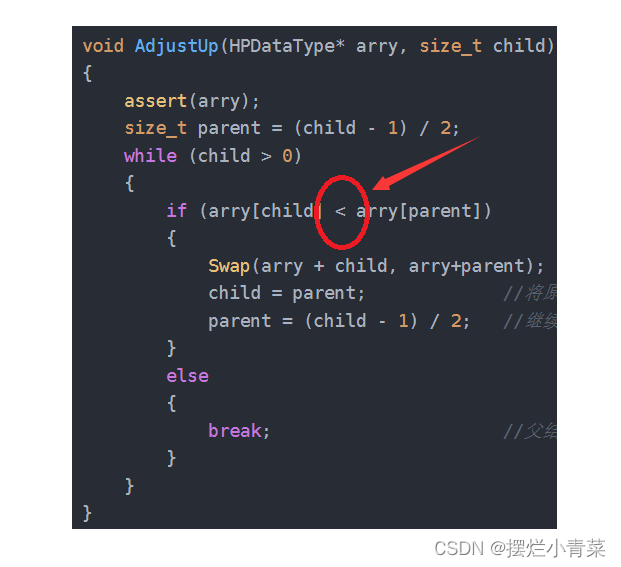
void AdjustUp(HPDataType* arry, size_t child) //child表示孩子结点的编号HPDataType是typedef定义的数据类型,arry是指向堆区数组的指针,child是待调整的结点在完全二叉树中的编号(物理上是其数组下标)
- 算法调用场景:
接口实现:
//元素交换接口 void Swap(HPDataType* e1, HPDataType* e2) {assert(e1 && e2);HPDataType tem = *e1;*e1 = *e2;*e2 = tem; }//小堆元素的向上调整接口 void AdjustUp(HPDataType* arry, size_t child) //child表示待调整的结点的编号 {assert(arry);size_t parent = (child - 1) / 2; //找到child结点的父结点while (child > 0) //child减小到0时则调整结束(说明待调整结点被调整到了根结点位置){if (arry[child] < arry[parent]) //父结点大于子结点,则子结点需要上调以保持小堆的结构{Swap(arry + child, arry+parent);child = parent; //将原父结点作为新的子结点继续迭代过程parent = (child - 1) / 2; //继续向上找另外一个父结点}else{break; //父结点不大于子结点,则堆结构任然成立,无需调整}} }
- 循环的结束分两种情况:
- child减小到0时,说明待调整结点被调整到了根结点的位置(小根堆数据结构恢复)
- 若某次父子结点比较中,父结点的值若大于子结点,则说明小根堆数据结构恢复,break跳出循环即可
- 调用该接口的前提是:待调整的结点的上层结构(包括待调整结点的所在层,但不包括待调整结点本身)满足小根堆的数据结构,比如:
否则的话堆元素的调整将失去意义(因为只有在满足上述前提的情况下,每次调用完该接口,待调整的结点的上层结构将保持小根堆的数据结构,并且以待调整结点为叶结点的上层结构会成为一个堆)
- 大根堆的元素向上调整算法接口:
- 若要将接口改为大根堆元素向上调整算法接口,只需将上图中的红圈中的小于号改为大于号即可
3.堆元素向下调整算法接口
函数首部:
void AdjustDown(HPDataType* arry,size_t size,size_t parent)HPDataType是typedef定义的数据类型,arry是指向堆区数组首地址的指针,size是堆的元素总个数,parent是待调整的结点在完全二叉树中的编号(物理上是其数组下标)
- 算法调用场景:
接口实现:
//元素交换接口 void Swap(HPDataType* e1, HPDataType* e2) {assert(e1 && e2);HPDataType tem = *e1;*e1 = *e2;*e2 = tem; }//小堆元素的向下调整接口 void AdjustDown(HPDataType* arry,size_t size,size_t parent) {assert(arry);size_t child = 2 * parent + 1; //确定父结点的左孩子的编号while (child < size) //child增加到大于或等于size时则调整结束{if (child + 1 < size && arry[child + 1] < arry[child]) //确定左右孩子中较小的孩子结点{++child;}if ( arry[child] < arry[parent])//父结点大于子结点,则子结点需要上调以保持小堆的结构{Swap(arry + parent, arry + child);parent = child; //将原子结点作为新的父结点继续迭代过程child = 2 * parent + 1; //继续向下找另外一个子结点}else{break; //父结点不大于子结点,则堆结构任然成立,无需调整}} }
- 算法需要注意的一些边界条件:
- child >= size说明被调整元素已经被交换到了叶结点的位置,小根堆数据结构恢复,终止循环
- 接口中,我们只设计了一个child变量来表示当前父结点的孩子结点编号,因此我们需要先确定左右孩子中哪一个结点值较小,令child等于较小的孩子结点的编号:
if (child + 1 < size && arry[child + 1] > arry[child]) //确定左右孩子中较小的孩子结点 {++child; }child + 1<size判断语句是为了确定当前父结点的右孩子是否存在;
调用该接口的前提是:待调整的结点位置的左右子树都满足小根堆的数据结构,比如:
否则的话堆元素的调整将失去意义(因为只有在满足上述前提的情况下,每次调用完该接口后,待调整的结点位置的左右子树将保持小根堆的数据结构,并且以待调整结点为根结点的子树会成为一个堆)
大根堆的元素向下调整算法接口:
若要实现大根堆的元素向下调整算法接口,我们只需将上图红圈中的两个小于号改为大于号即可
堆元素上下调整算法接口的实现原理分析参见:http://t.csdn.cn/MKzyt
http://t.csdn.cn/MKzyt
二.堆排序的实现
有了堆元素的上下调整算法接口后,我们便可以利用堆的数据结构来实现高效的排序算法.
现在我们给出一个一百个元素的数组(每个元素随机附一个值):
typedef int HPDataType; int main() {int arr[100] = { 0 };srand((unsigned int)time(NULL));for (int i = 0; i < 100; i++){arr[i] = rand() % 10000; //数组每个元素赋上一个随机值}return 0; }
堆排序函数接口:
void HeapSort(int * arr,int size);arr是指向待排序数组首地址的指针,size是待排序的数组的元素个数
1.空间复杂度为O(N)的堆排序(以排升序为例)
思路分析:
- 实现堆排序的其中一种非常暴力的思路是:
- 在HeapSort接口中动态开辟一个和待排序数组空间大小相同的Heap数组作为堆
- 然后将待排序数组的元素逐个尾插到Heap数组中同时调用堆元素向上调整算法调整堆尾元素的位置来建堆(排升序则建立小根堆)
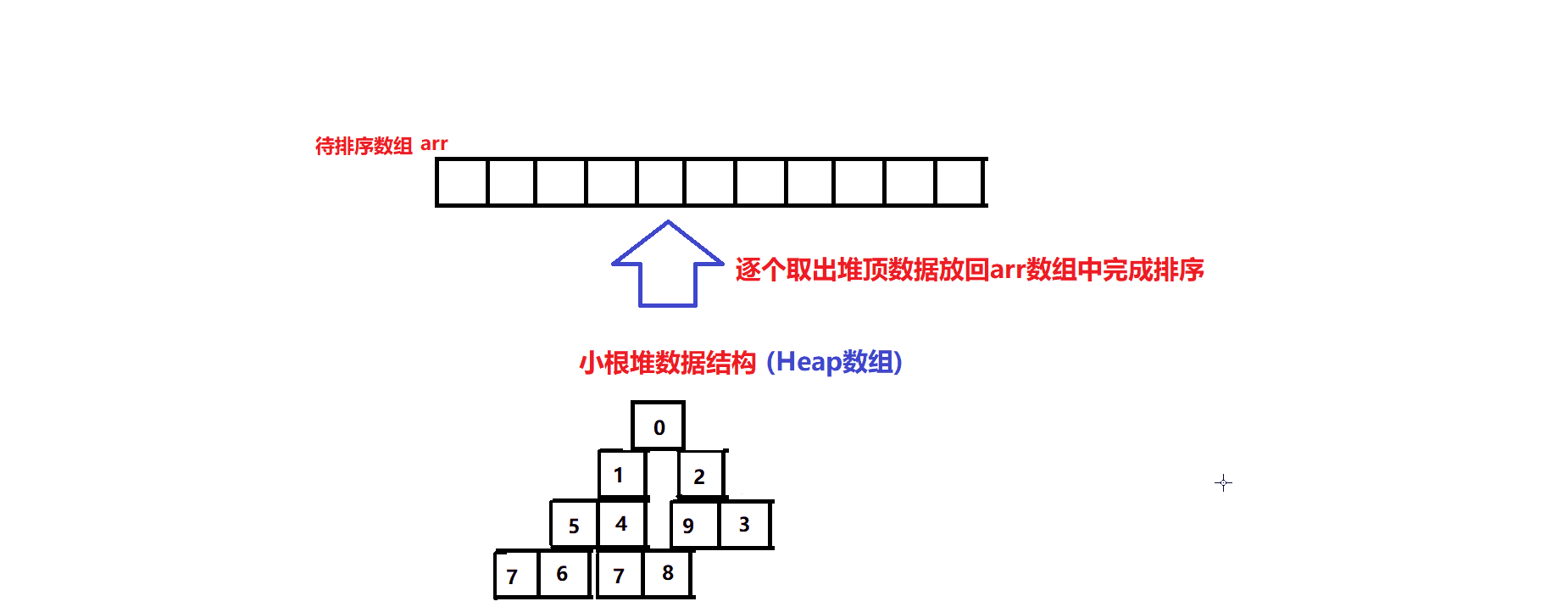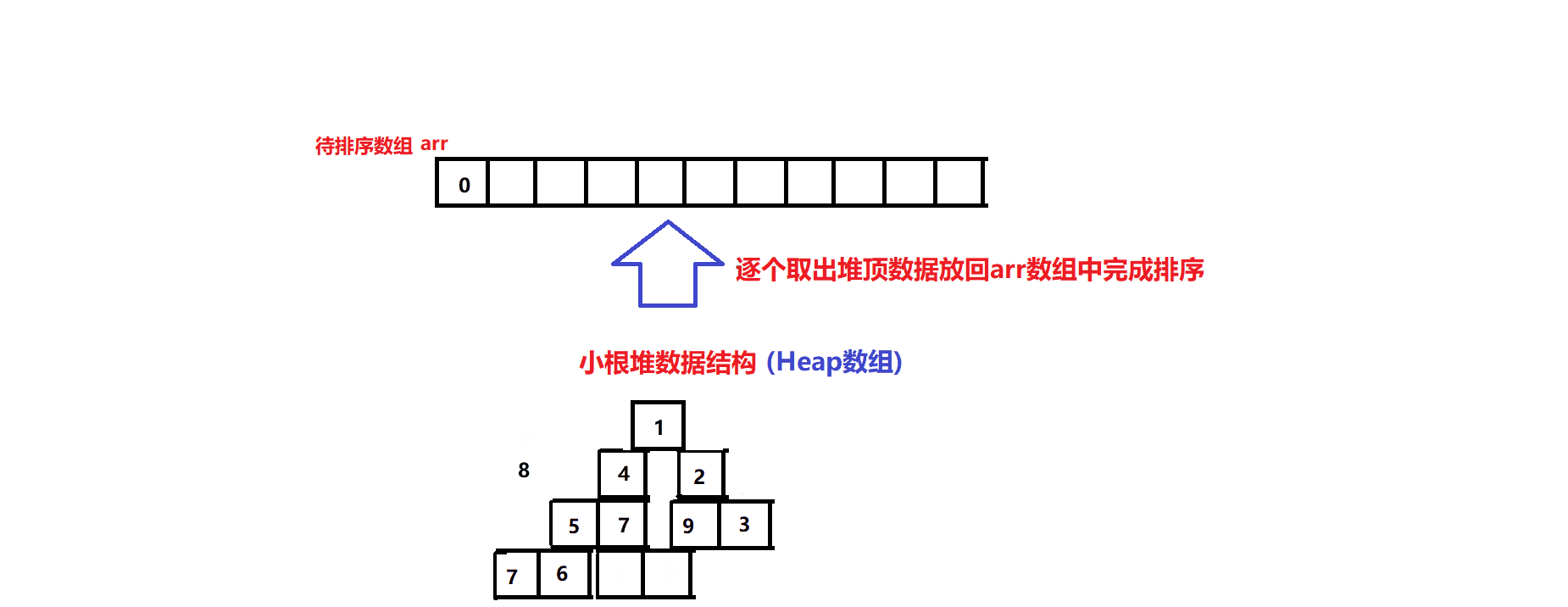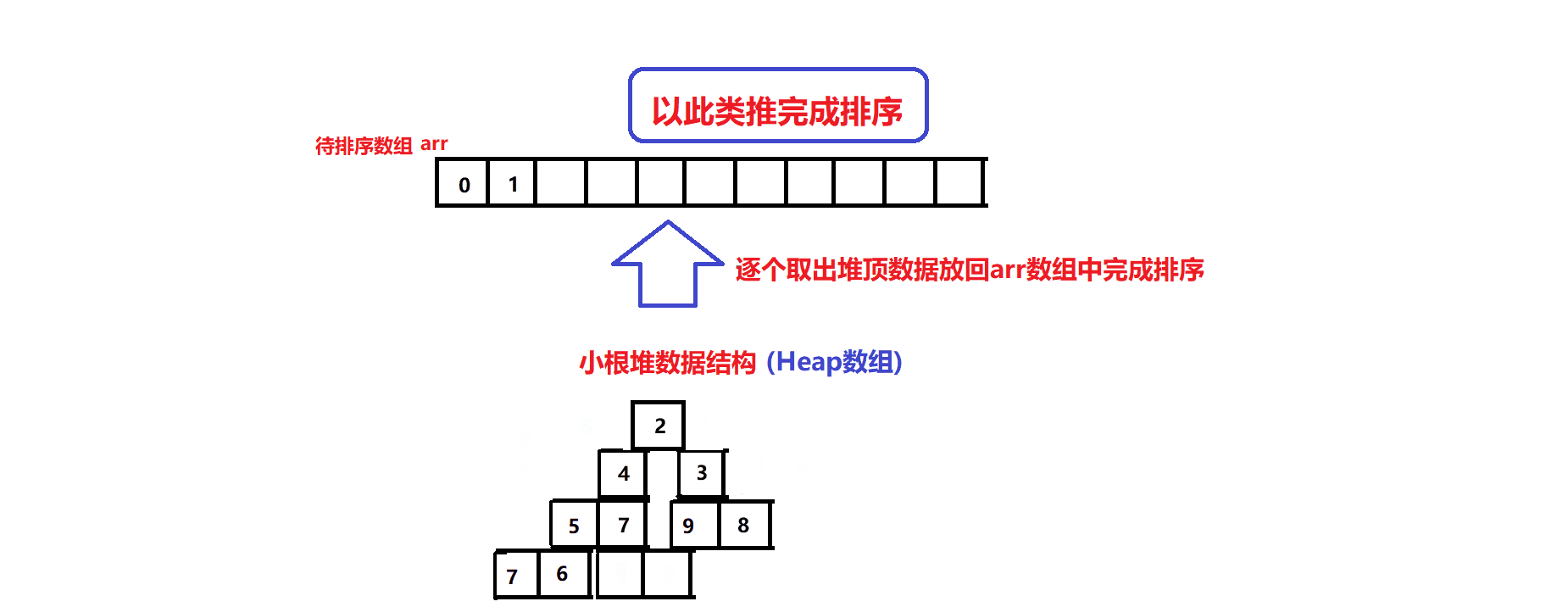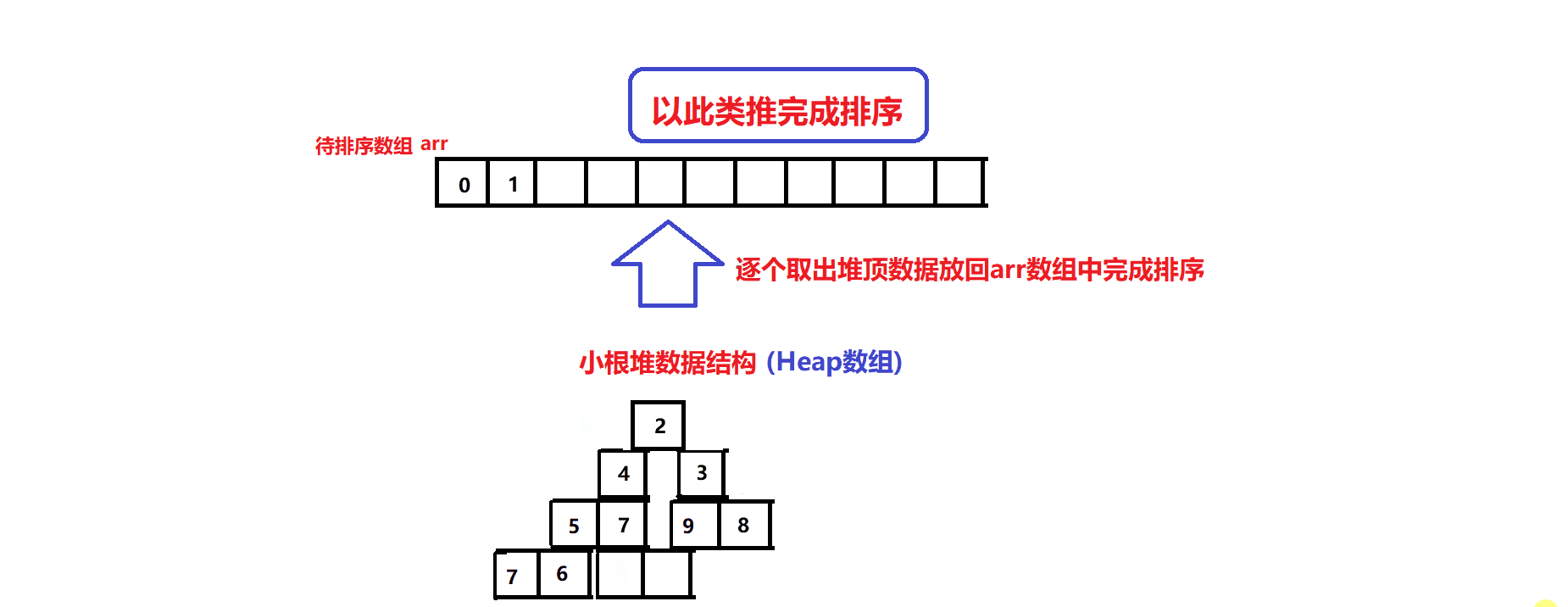
- 建堆过程完成后,再逐个取出堆顶数据(按照堆顶元素删除的方式取出,具体参见堆的实现http://t.csdn.cn/vhbJf)(堆顶数据为堆中的最小元素)从待排序数组首地址开始覆盖待排序数组的空间即可完成排序
排序算法图解:
- 先将arr中的元素逐个尾插到Heap数组中建堆
- 再逐个将Heap数组的堆顶元素利用堆顶元素删除操作放回到arr数组中,完成升序排序(其原理在于小根堆堆顶元素永远是堆中的最小元素)(堆顶元素删除操作指的是:先将堆顶元素与堆尾元素交换,维护堆尾的下标指针减一(堆元素个数减一),再将堆顶元素向下调整恢复小根堆数据结构):
代码实现:
//元素交换接口 void Swap(HPDataType* e1, HPDataType* e2) {assert(e1 && e2);HPDataType tem = *e1;*e1 = *e2;*e2 = tem; }//小堆元素的向上调整接口 void AdjustUp(HPDataType* arry, size_t child) //child表示待调整的结点的编号 {assert(arry);size_t parent = (child - 1) / 2; //找到child结点的父结点while (child > 0) //child减小到0时则调整结束(说明待调整结点被调整到了根结点位置){if (arry[child] < arry[parent]) //父结点大于子结点,则子结点需要上调以保持小堆的结构{Swap(arry + child, arry+parent);child = parent; //将原父结点作为新的子结点继续迭代过程parent = (child - 1) / 2; //继续向上找另外一个父结点}else{break; //父结点不大于子结点,则堆结构任然成立,无需调整}} }//小堆元素的向下调整接口 void AdjustDown(HPDataType* arry,size_t size,size_t parent) {assert(arry);size_t child = 2 * parent + 1; //确定父结点的左孩子的编号while (child < size) //child增加到大于或等于size时则调整结束{if (child + 1 < size && arry[child + 1] < arry[child]) //确定左右孩子中较小的孩子结点{++child;}if ( arry[child] < arry[parent])//父结点大于子结点,则子结点需要上调以保持小堆的结构{Swap(arry + parent, arry + child);parent = child; //将原子结点作为新的父结点继续迭代过程child = 2 * parent + 1; //继续向下找另外一个子结点}else{break; //父结点不大于子结点,则堆结构任然成立,无需调整}} }void HeapSort(int* arr, int size) {assert(arr);int* Heap = (int*)malloc(size * sizeof(int));assert(Heap);int ptrarr = 0; //维护arr数组的下标指针int ptrheap = 0; //维护Heap数组的下标指针//逐个尾插元素建堆while (ptrarr < size){Heap[ptrheap] = arr[ptrarr]; //将arr数组中的元素逐个尾插到Heap数组中AdjustUp(Heap, ptrheap); //每尾插一个元素就将该元素向上调整保持小堆的数据结构ptrheap++;ptrarr++;}//逐个将堆顶的元素放回arr数组(同时进行删堆操作)ptrarr = 0;int HeapSize = size;while (ptrarr < size){Swap(&Heap[0], &Heap[HeapSize - 1]); //交换堆顶和堆尾的元素arr[ptrarr] = Heap[HeapSize-1]; //将原堆顶元素插入arr数组中HeapSize--; //堆元素个数减一(完成堆数据弹出)ptrarr++; //维护arr的下标指针+1AdjustDown(Heap, HeapSize, 0); //将交换到堆顶的数据向下调整恢复堆的数据结构} }排序测试:
int main() {int arr[100] = { 0 };srand((unsigned int)time(NULL));for (int i = 0; i < 100; i++){arr[i] = rand() % 10000; //数组每个元素赋上一个随机值}HeapSort(arr, 100);for (int i = 0; i < 100; ++i){printf("%d ", arr[i]);}return 0; }
时空复杂度分析:
- 由于尾插建堆和堆顶删堆的时间复杂度都是O(NlogN),因此排序的时间复杂度为O(NlogN)
- 显然,在HeapSort接口中多开辟了一个Heap数组,排序的空间复杂度为O(N)
- 关于建堆和删堆的时间复杂度证明参见青菜的博客:http://t.csdn.cn/MKzyt
http://t.csdn.cn/MKzyt
- 该种堆排序代码量很大,数据并发量也很大,而且空间复杂度较高,接下来我们来实现一种最优良的堆排序算法
2. 空间复杂度为O(1)的堆排序(以排降序为例)
前面的堆排序算法中引入了Heap数组来建堆,浪费了很多空间。
实际上,我们可以在待排序数组上原地完成堆的构建(即将数组arr调整成堆).
将数组arr调整成堆的思路:
- 现有一个乱序数组arr,逻辑上我们将其看成一颗完全二叉树:
- 接下来我们尝试用堆的元素向下调整算法接口将arr调整成小根堆
- 调用堆元素向下调整接口的前提是:待调整的结点位置的左右子树都满足小根堆的数据结构(因为在满足这个前提的情况下,我们每次调用完该接口后待调整的结点位置的左右子树将保持小根堆的数据结构,并且以待调整结点为根结点的子树会成为一个堆)
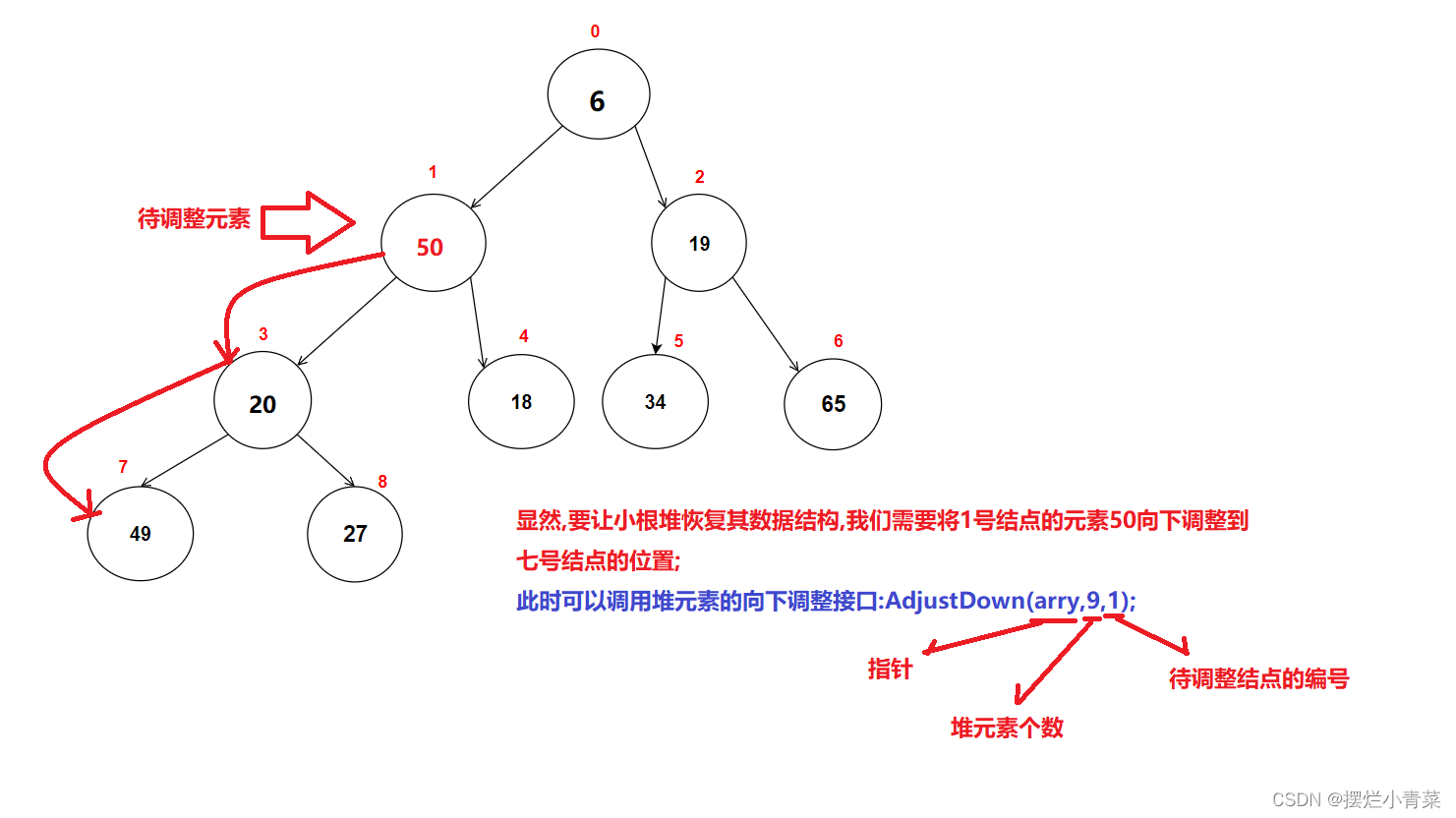
- 由上述前提可知,如果从堆顶(或中间任意一个位置的结点)元素开始调整堆是没有意义的,所以我们只能从堆尾的子结构开始调堆:
- 通过上图的分析,我们可以通过堆尾元素找到第一个要被向下调整的结点,然后从第一个要被向下调整的结点开始依次往前向下调整其他结点直到完成对树的根结点的向下调整之后,整颗完全二叉树就会被调整成堆:
- 调堆小动画:
- 实现将arr数组调整成小根堆的代码:
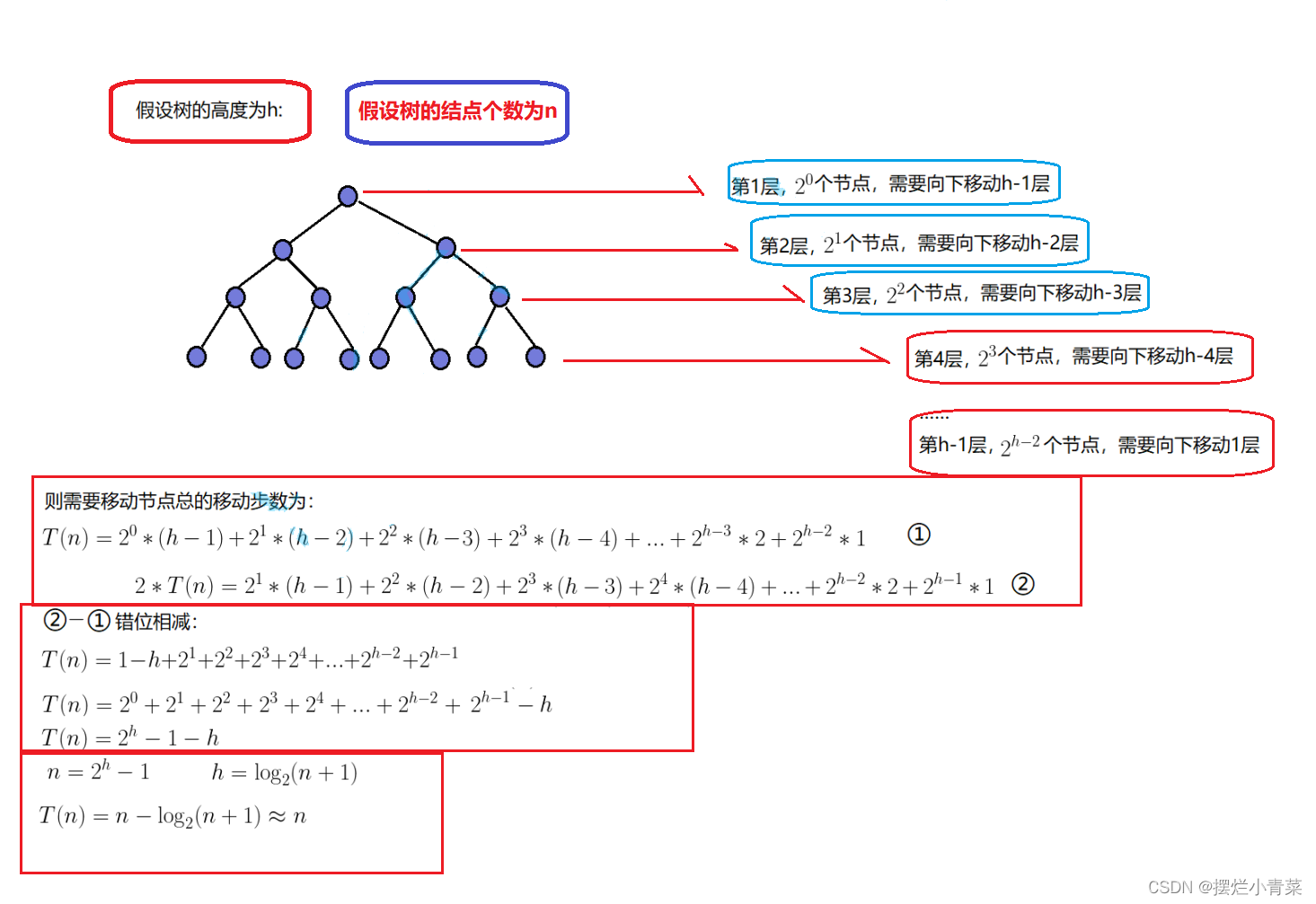
void HeapSort(int* arr, int size) {assert(arr);int parent = (size - 1 - 1) / 2; //找到第一个要被调整向下调整的元素for (; parent >= 0; --parent){AdjustDown(arr, size, parent); //逐个元素向下调整完成堆的构建} }将数组arr调整成堆的时间复杂度分析:
因此假设arr数组中有N个元素,将数组arr调整成堆的时间复杂度为:O(N)
在数组arr数组被调整成堆的基础上完成排序的思路
- 数组arr被调整成小根堆后,我们只需逐个删除堆顶元素就可以完成所有数的降序排序
- 堆元素删除操作指的是:先将堆顶元素与堆尾元素交换,维护堆尾的下标指针减一(堆元素个数减一),再将堆顶元素向下调整恢复小根堆数据结构)
- 逐个删除堆顶元素完成降序排序的过程图解:
- 由上述算法设计思路可知:为了完成堆排序我们只需额外设计一个堆元素向下调整接口
堆排序代码实现:
//元素交换接口 void Swap(HPDataType* e1, HPDataType* e2) {assert(e1 && e2);HPDataType tem = *e1;*e1 = *e2;*e2 = tem; }//小堆元素的向下调整接口 void AdjustDown(HPDataType* arry,size_t size,size_t parent) {assert(arry);size_t child = 2 * parent + 1; //确定父结点的左孩子的编号while (child < size) //child增加到大于或等于size时则调整结束{if (child + 1 < size && arry[child + 1] < arry[child]) //确定左右孩子中较小的孩子结点{++child;}if ( arry[child] < arry[parent])//父结点大于子结点,则子结点需要上调以保持小堆的结构{Swap(arry + parent, arry + child);parent = child; //将原子结点作为新的父结点继续迭代过程child = 2 * parent + 1; //继续向下找另外一个子结点}else{break; //父结点不大于子结点,则堆结构任然成立,无需调整}} }void HeapSort(int* arr, int size) {assert(arr);int parent = (size - 1 - 1) / 2; //找到第一个要被调整向下调整的元素for (; parent >= 0; --parent){AdjustDown(arr, size, parent); //逐个元素向下调整完成堆的构建}while (size > 0) //逐个删除堆顶元素完成降序排序,我们将size作为堆尾指针{Swap(&arr[0], &arr[size - 1]); //交换堆尾与堆顶元素size--; //堆尾指针减一,堆元素个数减一AdjustDown(arr, size, 0); //将堆顶元素向下调整恢复小根堆数据结构} }排序接口测试:
int main() {int arr[100] = { 0 };srand((unsigned int)time(NULL));for (int i = 0; i < 100; i++){arr[i] = rand() % 10000; //数组每个元素赋上一个随机值}HeapSort(arr, 100);for (int i = 0; i < 100; ++i){printf("%d ", arr[i]);}return 0; }
排序时空复杂度分析:
- 逐个删除堆顶元素直到将堆删空的时间复杂度为O(NlogN),证明分析参见青菜的博客:http://t.csdn.cn/vhbJf
http://t.csdn.cn/vhbJf
- 已知将arr数组调整成堆的时间复杂度为O(N),因此堆排序整体的时间复杂度为O(NlogN)
- 同时易知,堆排序算法的空间复杂度为O(1)
- 可见堆排序是一个非常高效的排序算法(至少比冒泡厉害多了)
三.用堆数据结构解决TopK问题
TopK问题指的是,从N个元素数组中,选出K个最值.(K<=N)
Leetcode上面有相关题型.
面试题 17.14. 最小K个数 - 力扣(Leetcode)
1. 问题描述:
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。(数组元素个数为arrSize)
(k<=arrSize)
示例:
输入: arr = [1,3,5,7,2,4,6,8], k = 4 输出: [1,2,3,4]
题解接口:
int* smallestK(int* arr, int arrSize, int k, int* returnSize) {}arrSize为题设数组的元素个数,k为要找出的最小数的个数,returnSize是结果数组的元素个数
2.问题分析与求解
- 本题如果直接对arr数组进行排序理论上是可以解决的,但是时间效率略低(O(NlogN)),有种杀鸡用牛刀的感觉
- 我们可以考虑利用堆数据结构来实现本题的最优解之一:
- 首先创建一个k*sizeof(int)字节大小的数组Heap用于存储堆
- 然后将arr中前k个元素尾插到Heap中建堆
- 然后将arr中后(arrSize-k)个元素逐个与Heap堆顶的元素比较,若arr中后(arrSize-k)个元素中的某元素小于Heap堆顶的元素,则将其与Heap堆顶元素交换,再将其进行向下调整保持堆的数据结构(元素交换入堆)
- 完成arr中后(arrSize-k)个元素与Heap堆顶的遍历比较后,堆中最后剩下的就是arr数组中最小的k个元素
算法图解:
算法的合理性证明:
- 由于大根堆的堆顶元素是堆中的最大元素,因此在arr中后(arrSize-k)个元素与Heap堆顶的遍历比较的过程中没有入堆的元素一定都大于堆中的k个元素,因此最终堆中的k个元素一定是arr数组中最小的k个元素
题解代码:
void Swap(int* e1 ,int* e2) {int tem = *e1;*e1 = *e2;*e2 = tem; }//大堆元素的向上调整接口 void AdjustUp(int * arry, size_t child) //child表示待调整结点的编号 {assert(arry);size_t parent = (child - 1) / 2;while (child > 0) //child减小到0时则调整结束{if (arry[child] > arry[parent]) //父结点小于子结点,则子结点需要上调以保持大堆的结构{Swap(arry + child, arry+parent);child = parent; //将原父结点作为新的子结点继续迭代过程parent = (child - 1) / 2; //继续向上找另外一个父结点}else{break; //父结点不小于子结点,则堆结构任然成立,无需调整}} }//大堆元素的向下调整接口 void AdjustDown(int * arry,size_t size,size_t parent) {assert(arry);size_t child = 2 * parent + 1; //确定父结点的左孩子的编号while (child < size) //child增加到大于或等于size时则调整结束{if (child + 1 < size && arry[child + 1] > arry[child]) //确定左右孩子中较大的孩子结点{++child;}if ( arry[child] > arry[parent])//父结点小于子结点,则子结点需要上调以保持大堆的结构{Swap(arry + parent, arry + child);parent = child; //将原子结点作为新的父结点继续迭代过程child = 2 * parent + 1; //继续向下找另外一个子结点}else{break; //父结点不小于子结点,则堆结构任然成立,无需调整}} }int* smallestK(int* arr, int arrSize, int k, int* returnSize) {if(0==k){*returnSize =0;return NULL;}int * Heap = (int*)malloc(k*sizeof(int));*returnSize = k; //创建一个空间大小为k的数组用于存储堆int ptrHeap =0; //维护堆尾的指针while(ptrHeap<k) //将arr数组前k个元素尾插到Heap中完成建堆{Heap[ptrHeap]=arr[ptrHeap];AdjustUp(Heap,ptrHeap); ptrHeap++;}int ptrarr = k; //用于遍历arr中后(arrSize-k)个元素的下标指针while(ptrarr < arrSize) //将arr中后(arrSize-k)个元素逐个与Heap堆顶的元素进行比较{//如果找到arr中后(arrSize-k)个元素中比堆顶元素小的元素则将该元素替换入堆//并通过堆元素向下调整接口保持大根堆的数据结构if(Heap[0]>arr[ptrarr]){Swap(&Heap[0],&arr[ptrarr]);AdjustDown(Heap,k,0);}ptrarr++;}return Heap; //返回Heap数组作为及结果 }
算法时空复杂度分析:
设数组arr元素个数为N
- 建立Heap数组堆的时间复杂度为O(klogk)
- arr后(N-k)个元素与heap堆顶元素比较并入堆的时间复杂度为O((N-k)logk)(在最坏的情况下,arr后(N-k)个元素每个都进行了交换入堆并且被调整到了堆的叶子结点位置)
- 因此算法的总体时间复杂度为O(Nlogk)
- 易知算法的空间复杂度为O(k)
TopK问题的求解思想有着十分重要的实际意义:
比如在硬盘中有十亿个数据,我们想选出其中的100个最小值,那么利用上面的算法思想我们就可以在极少的内存消耗,极高的时间效率下完成这个工作.

相关文章:

八大排序算法之堆排序的实现+经典TopK问题
目录 一.堆元素的上下调整接口 1.前言 2.堆元素向上调整算法接口 3.堆元素向下调整算法接口 二.堆排序的实现 1.空间复杂度为O(N)的堆排序(以排升序为例) 思路分析: 代码实现: 排序测试: 时空复杂度分析: 2. 空间复杂度为O(1)的堆排序(以排降序为例) 将数组arr调…...
使用AppSmith(PagePlug )低代码平台快速构建小程序应用实践
文章目录一、入门(一)介绍(二)功能特性(三)体验一下(四)参考教程二、使用Appsmith构建商城微信小程序(一)说明(二)应用配置࿰…...

第52章 短信验证服务和登录的后端定义实现
1 Services.Messages.SmsValidate using Core.Domain.Messages; using Data; using Microsoft.EntityFrameworkCore; namespace Services.Messages { /// <summary> /// 【短信验证服务--类】 /// <remarks> /// 摘要: /// 通过类中的方法成员实…...
谷歌验证码的使用
1. 表单重复提交之验证码 1.1 表单重复提交三种常见情况 提交完表单。服务器使用请求转来进行页面跳转。这个时候,用户按下功能键 F5,就会发起最后一次的请求。造成表单重复提交问题。解决方法:使用重定向来进行跳转用户正常提交服务器&…...
- git的安装与配置)
Git学习入门(1)- git的安装与配置
title: git学习(1) - git的安装与配置CSDN: https://blog.csdn.net/jj6666djdbbd?typeblogBlog: https://helloylh.comGithub: https://github.com/luumodtags: gitabbrlink: 12001description: 本文主要讲解了git的安装,配置基本工作date: …...

【Python】使用Playwright断言方法验证网页和Web应用程序状态
作为测试框架,Playwright 提供了一系列断言方法,您可以使用它们来验证网页和 Web 应用程序的状态。在这篇博客中,田辛老师将介绍 Playwright 中可用的各种断言方法,并为每种方法提供示例。 assert page.url() expected_url &…...

libgdx导入blender模型
具体就是参考 官网 https://libgdx.com/wiki/graphics/3d/importing-blender-models-in-libgdx blender 教程可以看八个案例教程带你从0到1入门blender【已完结】 这里贴一下过程图。 1.初始环境搭建略过。 2.打开blender 选中摄像机和灯光,右键进行删除。 3.选中…...
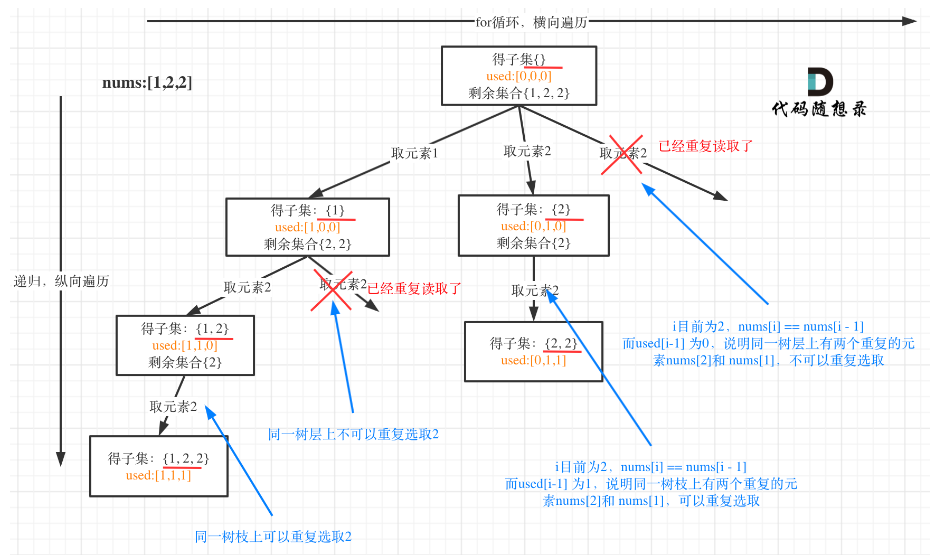
【20230227】回溯算法小结
回溯法又叫回溯搜索法,是搜索的一种方式。回溯法本质是穷举所有可能。如果想让回溯法高效一些,可以加一些剪枝操作。回溯算法解决的经典问题:组合问题切割问题子集问题排列问题棋盘问题如何去理解回溯法?回溯法解决的问题都可以抽…...
centos安装rocketmq
centos安装rocketmq1 下载rocketmq二进制包2 解压二进制包3 修改broker.conf4 修改runbroker.sh和runserver.sh的JVM参数5 启动NameServer和Broker6 安装rockermq dashboard(可视化控制台)1 下载rocketmq二进制包 点击rocketmq二进制包下载地址,下载完成之后通过ft…...
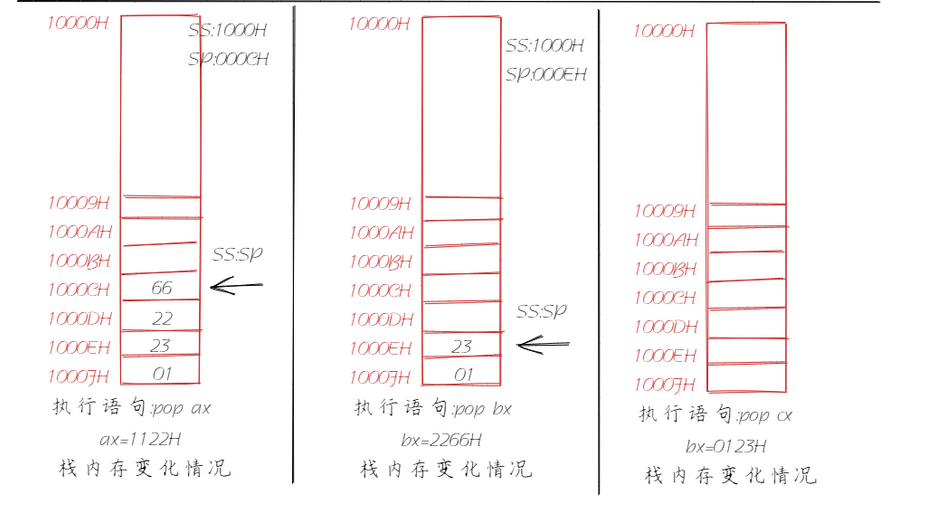
汇编语言程序设计(二)之寄存器
系列文章 汇编语言程序设计(一) 寄存器 在学习汇编的过程中,我们经常需要操作寄存器,那么寄存器又是什么呢?它是用来干什么的? 它有什么分类?又该如何操作?… 你可能会有许多的…...

华为OD机试Golang解题 - 单词接龙 | 独家
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

Elasticsearch的搜索命令
Elasticsearch的搜索命令 文章目录Elasticsearch的搜索命令数据准备URI Searchq(查询字符串)analyzer(指定查询字符串时使用的分析器)df(指定查询字段)_source(指定返回文档的字段)s…...

为什么人们宁可用Lombok,也不把成员设为public?
目录专栏导读一、从零了解JavaBean1、基本概念2、JavaBean的特征3、JavaBean的优点二、定义最简单的JavaBean三、思考一个问题,为何属性是private,然后用get/set方法?四、下面系统的分析以下,why?五、不和谐的声音,禁…...
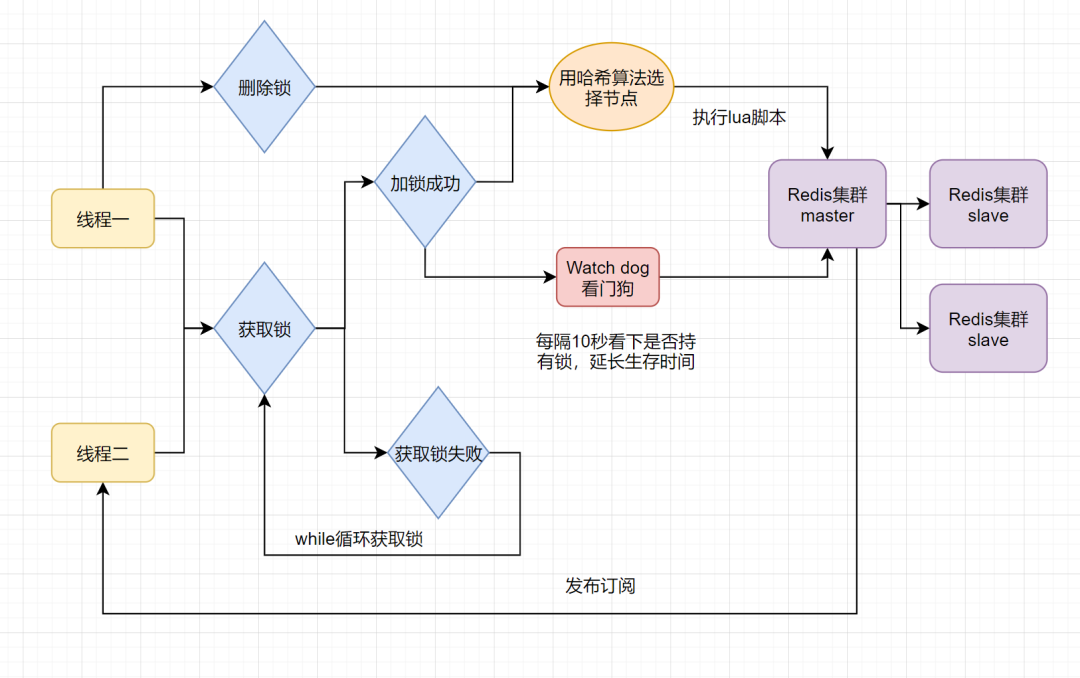
【Redis】Redis 如何实现分布式锁
Redis 如何实现分布式锁1. 什么是分布式锁1.1 分布式锁的特点1.2 分布式锁的场景1.3 分布式锁的实现方式2. Redis 实现分布式锁2.1 setnx expire2.2 set ex px nx2.3 set ex px nx 校验唯一随机值,再删除2.4 Redisson 实现分布式锁1. 什么是分布式锁 分布式锁其实…...
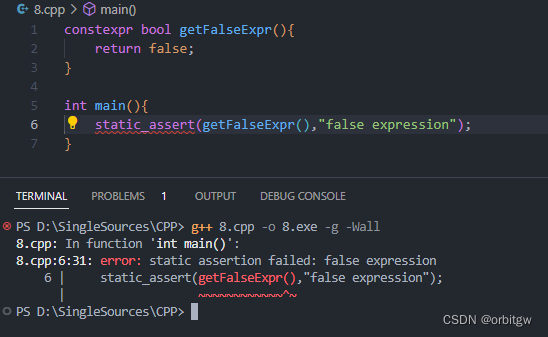
C++ 断言
文章目录前言assertstatic_assert前言 断言(Assertion)是一种常用的编程手段,用于排除程序中不应该出现的逻辑错误。它是一种很好的Debug工具。其作用是判断表达式是否为真。C提供了assert和static_assert来进行断言。在C库中也有断言,其中断言与C的相同…...
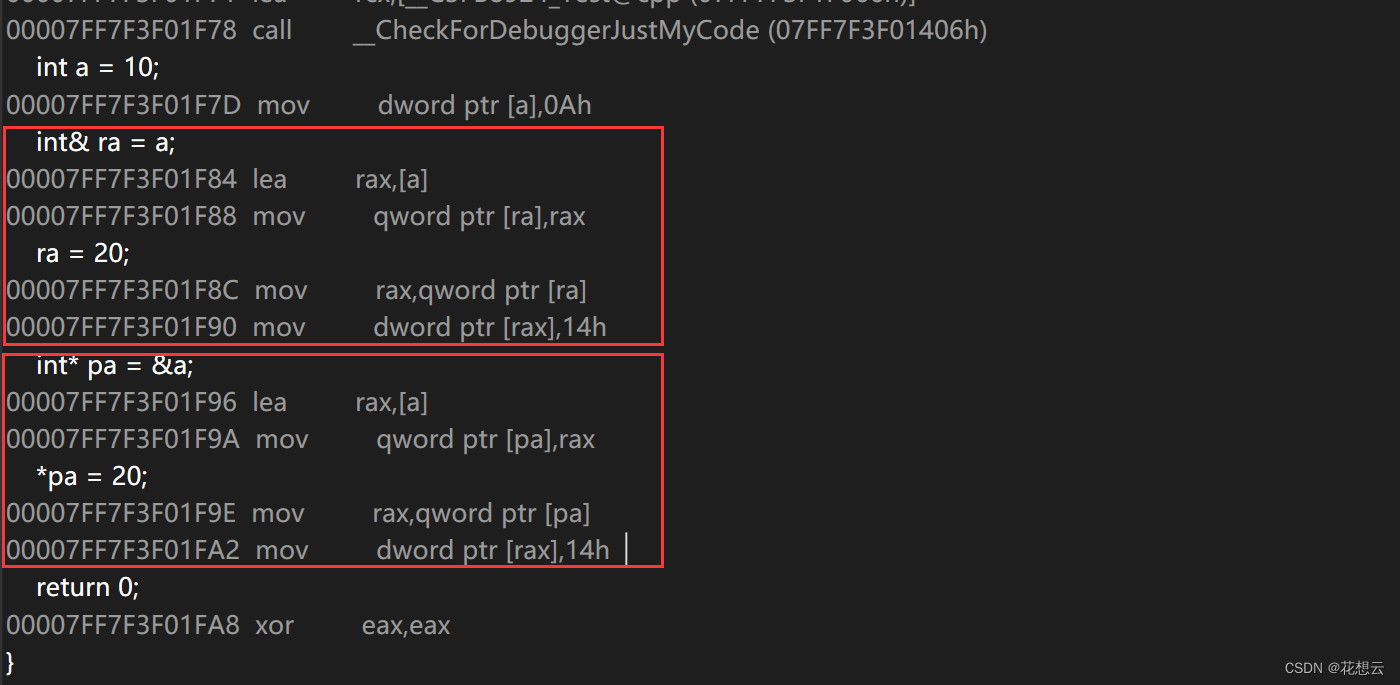
C++修炼之练气期第五层——引用
目录 1.引用的概念 2.引用的性质 3.常量引用 4.使用场景 1.作参数 2.作返回值 5.传值与传引用的效率比较 6.值和引用作为返回值的性能比较 7.引用与指针 指针与引用的不同点 要说C语言中哪个知识点最难学难懂,大部分人可能和我一样的答案——指针。C既然…...
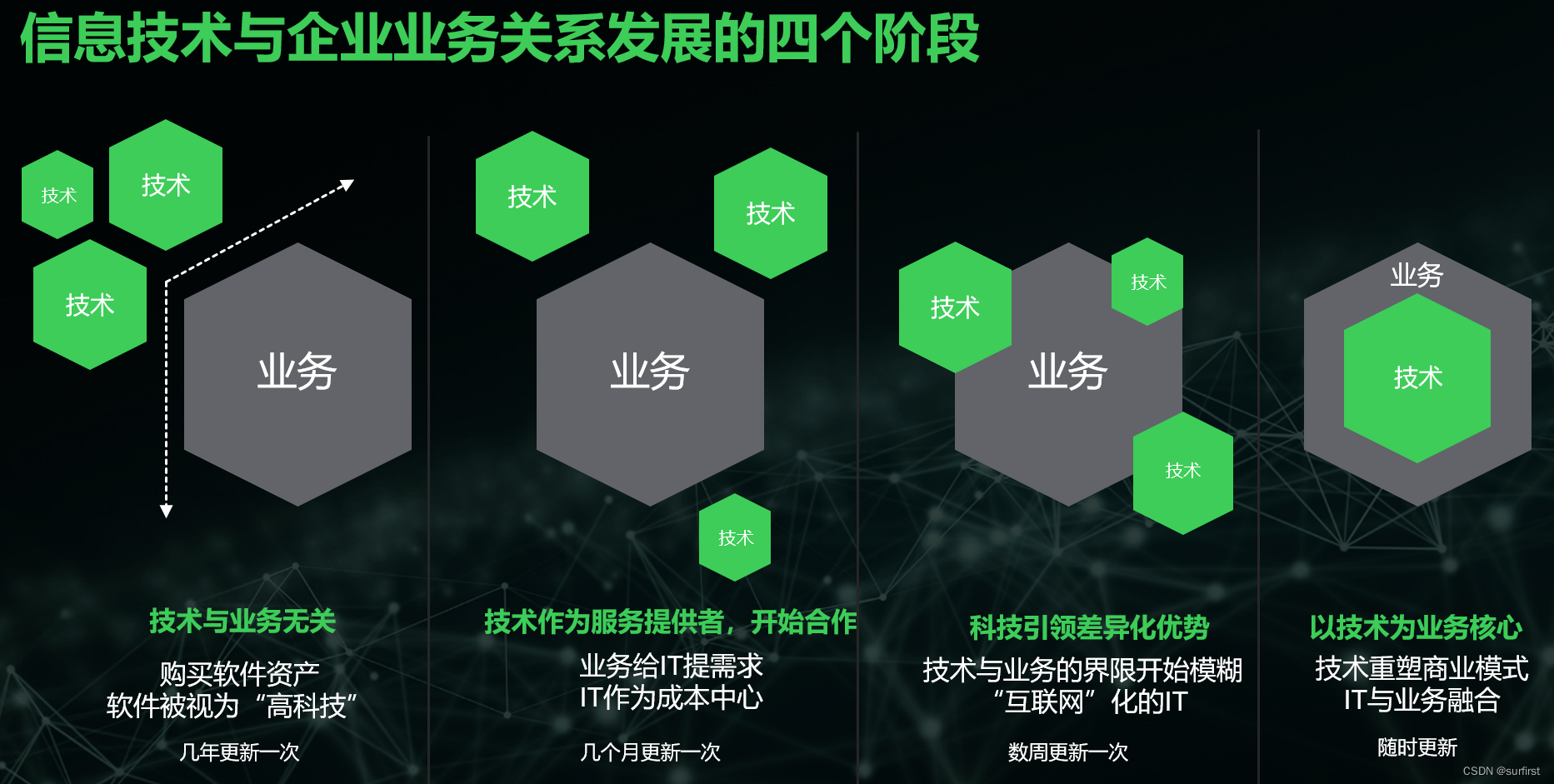
从企业数字化发展的四个阶段,看数字化创新战略
《Edge: Value-Driven Digital Transformation》一书根据信息技术与企业业务发展的关系把企业的数字化分为了四个阶段: 技术与业务无关技术作为服务提供者开始合作科技引领差异化优势以技术为业务核心 下图展示了这四个阶段的特点: 通过了解和分析各个…...
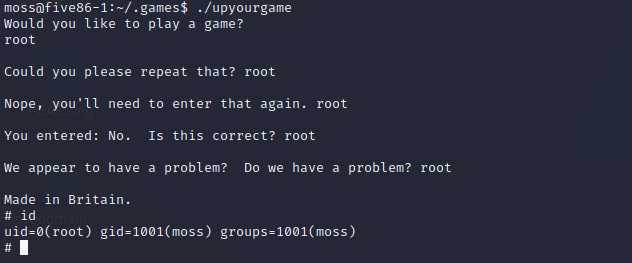
vulnhub five86-1
总结:私钥登录,隐藏文件很多 目录 下载地址 漏洞分析 信息收集 网站渗透 爆破密码 提权 下载地址 Five86-1.zip (Size: 865 MB)Download (Mirror): https://download.vulnhub.com/five86/Five86-1.zip使用:下载以后打开压缩包,使用vm直…...

28个案例问题分析---01---redis没有及时更新问题--Redis
redis没有及时更新问题一:背景介绍二:前期准备pom依赖连接Redis工具类连接mysql工具类三:过程使用redis缓存,缓存用户年龄业务对应流程图使用redis缓存用户年龄对应代码四:总结一:背景介绍 业务中使用redis…...
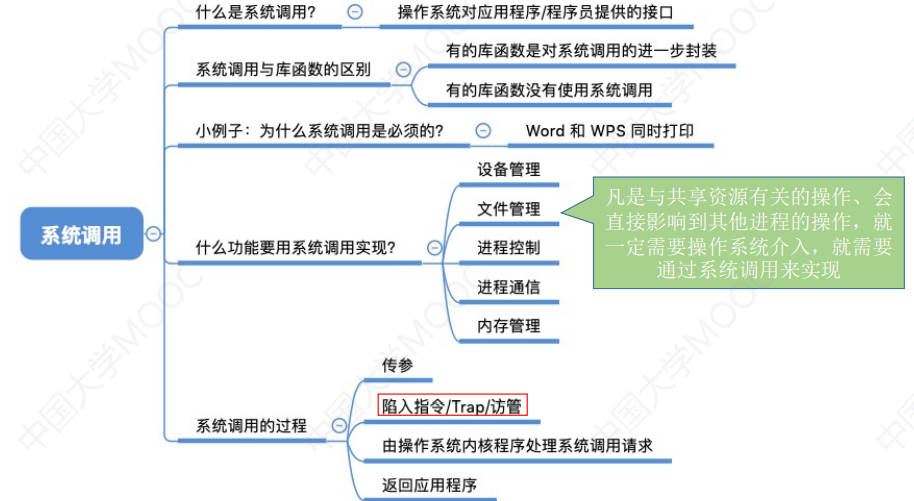
[1.3_3]计算机系统概述——系统调用
文章目录第一章 计算机系统概述系统调用(一)什么是系统调用,有何作用(二)系统调用与库函数的区别(三)小例子:为什么系统调用是必须的(四)什么功能要用到系统调…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

[QMT量化交易小白入门]-六十二、ETF轮动中简单的评分算法如何获取历史年化收益32.7%
本专栏主要是介绍QMT的基础用法,常见函数,写策略的方法,也会分享一些量化交易的思路,大概会写100篇左右。 QMT的相关资料较少,在使用过程中不断的摸索,遇到了一些问题,记录下来和大家一起沟通,共同进步。 文章目录 相关阅读1. 策略概述2. 趋势评分模块3 代码解析4 木头…...

第2课 SiC MOSFET与 Si IGBT 静态特性对比
2.1 输出特性对比 2.2 转移特性对比 2.1 输出特性对比 器件的输出特性描述了当温度和栅源电压(栅射电压)为某一具体数值时,漏极电流(集电极电流...