【20230227】回溯算法小结
回溯法又叫回溯搜索法,是搜索的一种方式。
回溯法本质是穷举所有可能。如果想让回溯法高效一些,可以加一些剪枝操作。
回溯算法解决的经典问题:
组合问题
切割问题
子集问题
排列问题
棋盘问题
如何去理解回溯法?
回溯法解决的问题都可以抽象为树形结构,回溯法解决的是在集合中递归查找子集,集合的大小构成树的宽度,递归的深度构成树的深度。
递归就要有终止条件,所以必然是一颗高度有限的树(N叉树)
回溯法模板
回溯三部曲
回溯函数模板返回值以及参数(一般返回值都为void)
回溯函数终止条件
if(终止条件){存放结果;return;
}回溯搜索的遍历过程
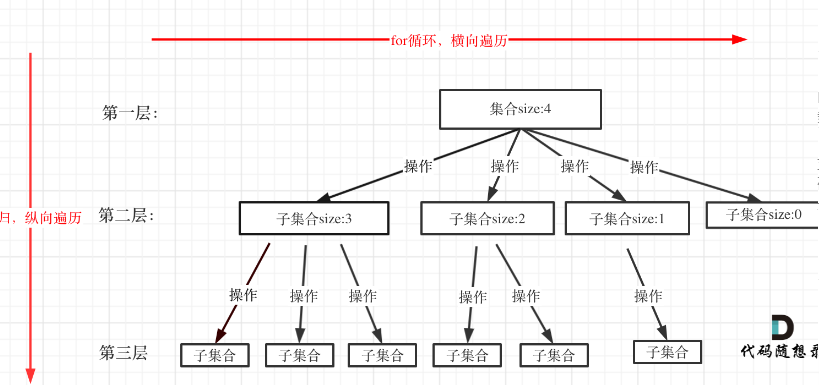
for(选择:本层集合中的元素(树中节点孩子的数量就是集合的大小)){处理节点;backtracking(路径,选择列表);//递归回溯,撤销处理结果
}组合问题
组合
在for循环中,i的结束条件可以优化,即:
列表剩余元素个数n-i+1>=所需元素个数k-path.size(),i<=n-k+path.size()+1。
组合总和 | 无重复数 | 可重复取 |
组合总和II | 有重复数 | 不可重复取 |
组合总和III | 无重复数 | 不可重复取 |
组合总和IV | 无重复数 | 可重复取,且有排列(动规问题) |
组合总和III
电话号码的字组合
数字与字母的映射问题可以用map,也可以用一个二维数组;
将char型转为int型,用char-‘0’的方式。
组合总和
可以重复使用元素,所以startIndex直接等于i就行了,不能直接每次都从0开始(这是排列的情况,会有重复出现);
组合总和II
集合中出现了重复元素,如果用之前的常规做法,会出现下面重复的情况,因此需要去重工作。
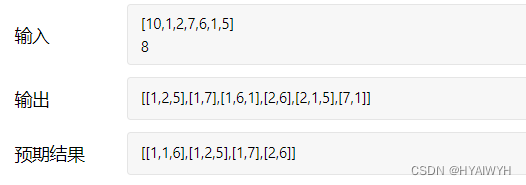
组合总和IV
用回溯超时了,是动态规划问题。
切割问题
分割回文串
如何切割的问题--确定分割点,例如abcdef,切割一个a后,在bvdef中再去切割第二段
如何判断为回文串--写一个bool型函数,专门用来判断
注意:截取子字符串substr(n,m)表示从下标n开始取m个元素。
复原IP地址
如何切割的问题,确定切割点,插入.号,用已经插入.号的数量来判断是否结束
如何判断是否为有效IP地址
注意一些细节问题:
string中插入 insert 擦除erase,因为已经插入.号,因此下一层递归开始应该在i+2处
除了只有一个0以外,以0开头的数字不合法;大于255不合法;
bool isValid(string& s,int left,int right){if(left>right) return false;if(s[left]=='0'&&left!=right) return false;int x=stoi(s.substr(left,right-left+1));if(x<=255) return true;else return false;}子集问题
子集 (不含重复元素)
子集问题是找树的所有节点,而组合和分割问题都是收集树的叶子节点。
每个节点都需要保存,所以先存,再判断终止条件。
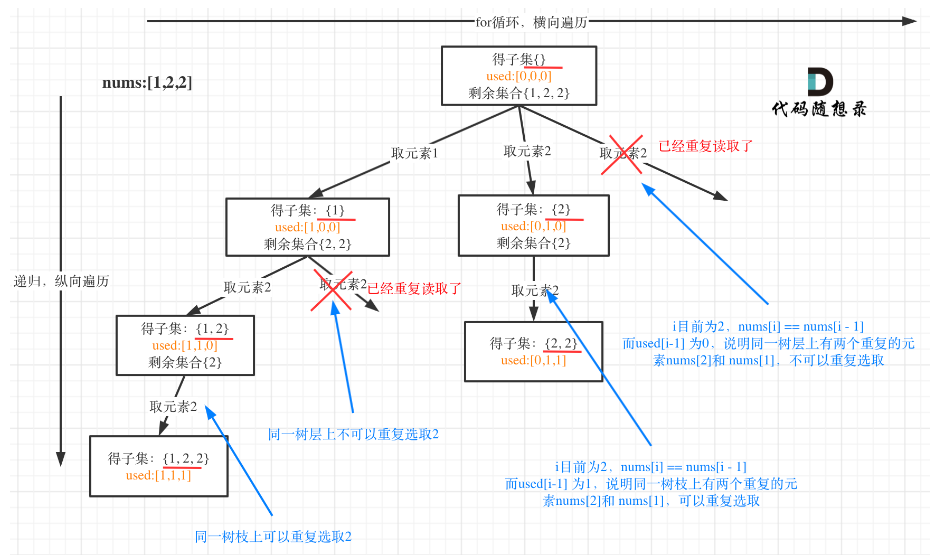
子集II (含有重复元素)
在同一层中不可选取相同元素,属于树层去重。
其实树层去重可以不用used数组,直接排序后判断相邻的数是否相同就可以完成树层去重。
注意:去重都需要排序!!!
递增子序列
需要解决的问题:
去重问题,仍然是树层的去重,但是不能对数组进行排序了,于是用哈希表进行去重;
选取的是符合条件的每个节点,其实可以与之前的联系起来,相当于可以不用写终止条件;
排列问题
全排列(没有重复元素)
排列问题就不需要startIndex了,需要使用used数组,来确定该数字在path中已经被取过了。
全排列II(有重复元素)
使用used数组+哈希表进行树枝去重和数层去重。
棋盘问题
重新安排行程
一个起飞机场对应多个降落机场、并且降落机场是有序的。所以映射后的降落机场用map去存。
map中所有元素都是pair,pair中第一个元素为key值(键值),第二个元素为value(实值)。
所有元素都会根据元素的键值自动排序。
unordered_map<string,map<string,int>> targets
相关文章:

【20230227】回溯算法小结
回溯法又叫回溯搜索法,是搜索的一种方式。回溯法本质是穷举所有可能。如果想让回溯法高效一些,可以加一些剪枝操作。回溯算法解决的经典问题:组合问题切割问题子集问题排列问题棋盘问题如何去理解回溯法?回溯法解决的问题都可以抽…...
centos安装rocketmq
centos安装rocketmq1 下载rocketmq二进制包2 解压二进制包3 修改broker.conf4 修改runbroker.sh和runserver.sh的JVM参数5 启动NameServer和Broker6 安装rockermq dashboard(可视化控制台)1 下载rocketmq二进制包 点击rocketmq二进制包下载地址,下载完成之后通过ft…...
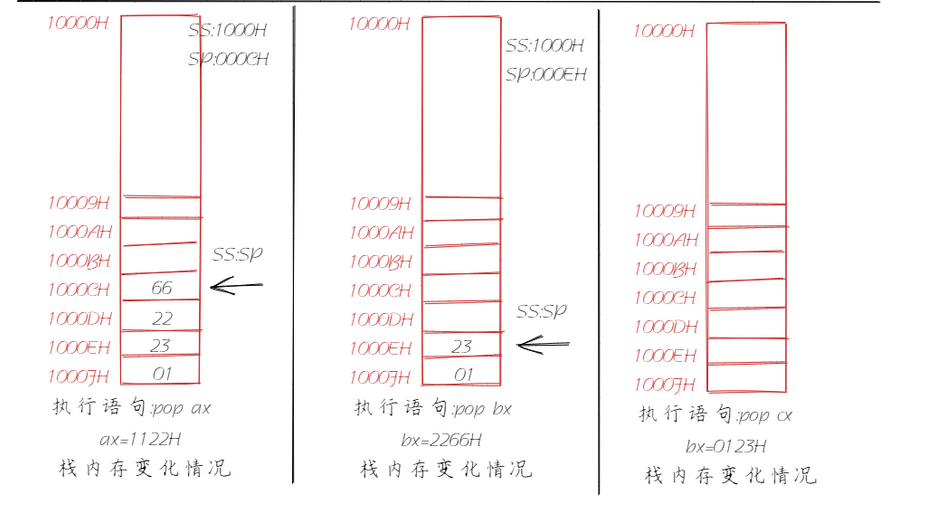
汇编语言程序设计(二)之寄存器
系列文章 汇编语言程序设计(一) 寄存器 在学习汇编的过程中,我们经常需要操作寄存器,那么寄存器又是什么呢?它是用来干什么的? 它有什么分类?又该如何操作?… 你可能会有许多的…...

华为OD机试Golang解题 - 单词接龙 | 独家
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

Elasticsearch的搜索命令
Elasticsearch的搜索命令 文章目录Elasticsearch的搜索命令数据准备URI Searchq(查询字符串)analyzer(指定查询字符串时使用的分析器)df(指定查询字段)_source(指定返回文档的字段)s…...

为什么人们宁可用Lombok,也不把成员设为public?
目录专栏导读一、从零了解JavaBean1、基本概念2、JavaBean的特征3、JavaBean的优点二、定义最简单的JavaBean三、思考一个问题,为何属性是private,然后用get/set方法?四、下面系统的分析以下,why?五、不和谐的声音,禁…...
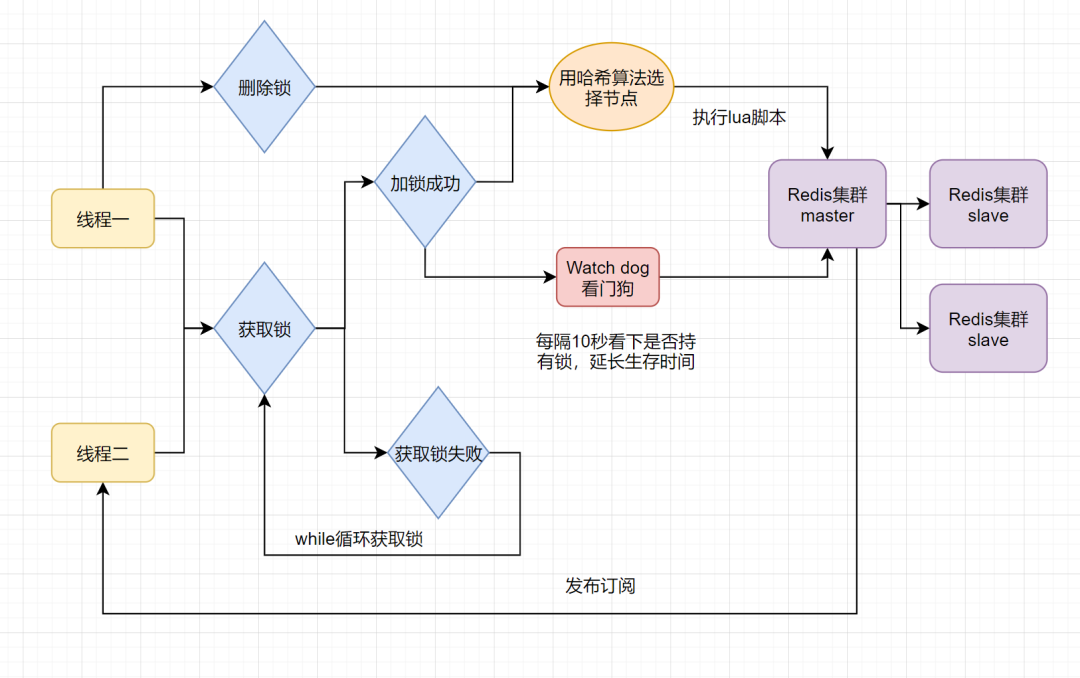
【Redis】Redis 如何实现分布式锁
Redis 如何实现分布式锁1. 什么是分布式锁1.1 分布式锁的特点1.2 分布式锁的场景1.3 分布式锁的实现方式2. Redis 实现分布式锁2.1 setnx expire2.2 set ex px nx2.3 set ex px nx 校验唯一随机值,再删除2.4 Redisson 实现分布式锁1. 什么是分布式锁 分布式锁其实…...
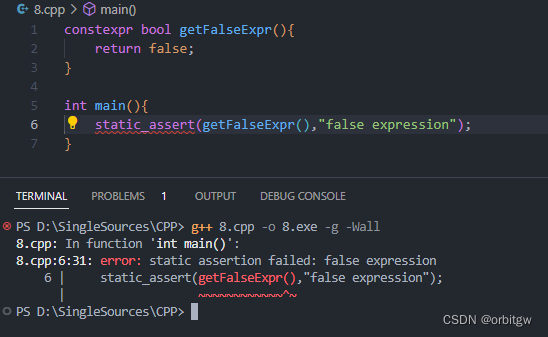
C++ 断言
文章目录前言assertstatic_assert前言 断言(Assertion)是一种常用的编程手段,用于排除程序中不应该出现的逻辑错误。它是一种很好的Debug工具。其作用是判断表达式是否为真。C提供了assert和static_assert来进行断言。在C库中也有断言,其中断言与C的相同…...
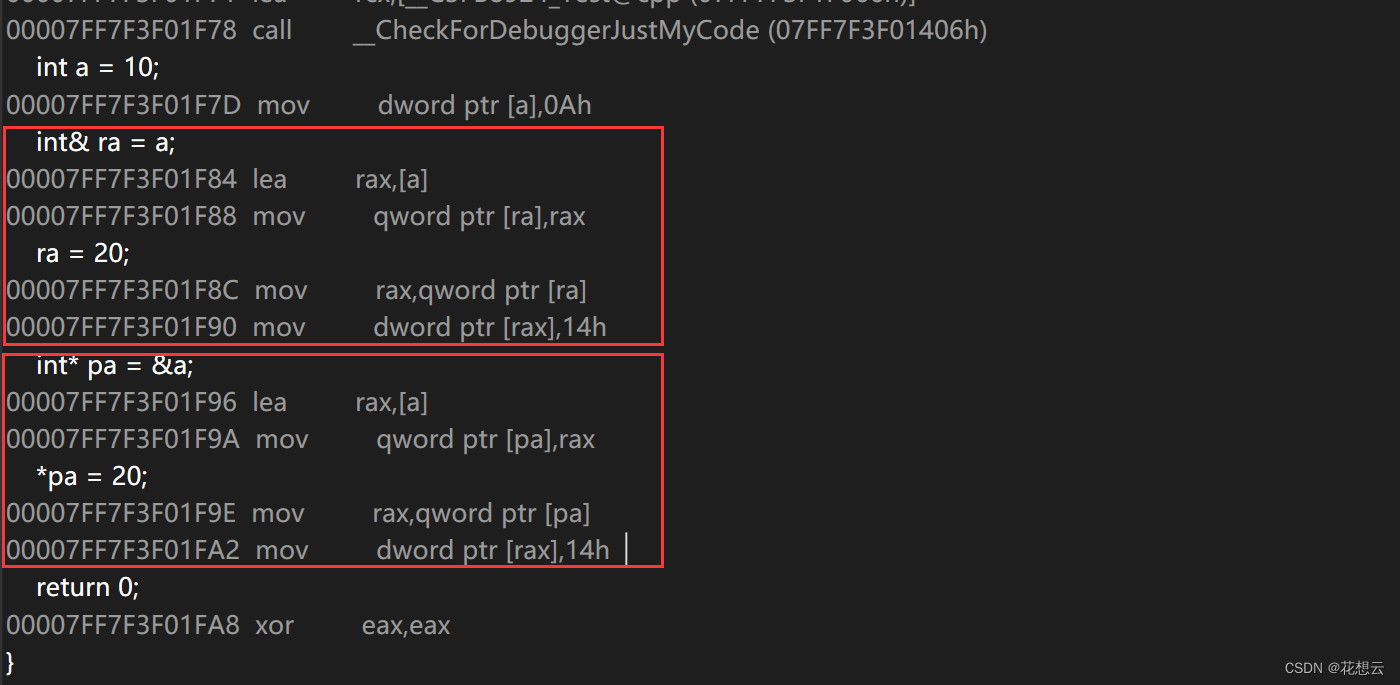
C++修炼之练气期第五层——引用
目录 1.引用的概念 2.引用的性质 3.常量引用 4.使用场景 1.作参数 2.作返回值 5.传值与传引用的效率比较 6.值和引用作为返回值的性能比较 7.引用与指针 指针与引用的不同点 要说C语言中哪个知识点最难学难懂,大部分人可能和我一样的答案——指针。C既然…...
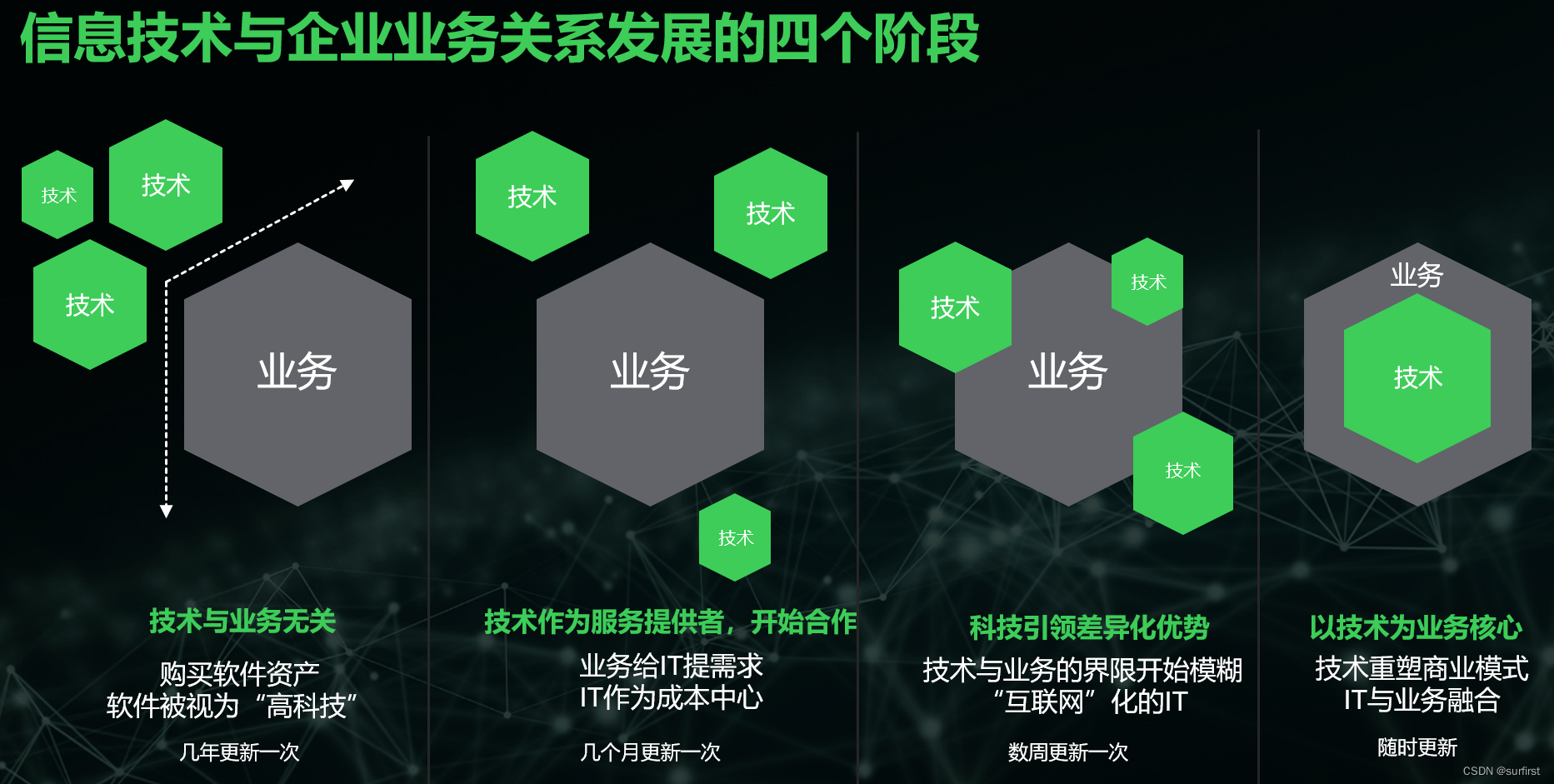
从企业数字化发展的四个阶段,看数字化创新战略
《Edge: Value-Driven Digital Transformation》一书根据信息技术与企业业务发展的关系把企业的数字化分为了四个阶段: 技术与业务无关技术作为服务提供者开始合作科技引领差异化优势以技术为业务核心 下图展示了这四个阶段的特点: 通过了解和分析各个…...
vulnhub five86-1
总结:私钥登录,隐藏文件很多 目录 下载地址 漏洞分析 信息收集 网站渗透 爆破密码 提权 下载地址 Five86-1.zip (Size: 865 MB)Download (Mirror): https://download.vulnhub.com/five86/Five86-1.zip使用:下载以后打开压缩包,使用vm直…...

28个案例问题分析---01---redis没有及时更新问题--Redis
redis没有及时更新问题一:背景介绍二:前期准备pom依赖连接Redis工具类连接mysql工具类三:过程使用redis缓存,缓存用户年龄业务对应流程图使用redis缓存用户年龄对应代码四:总结一:背景介绍 业务中使用redis…...
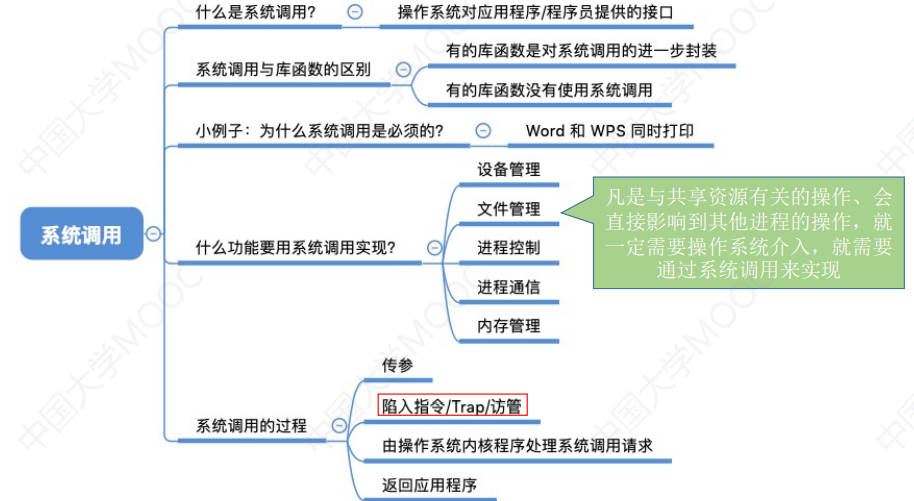
[1.3_3]计算机系统概述——系统调用
文章目录第一章 计算机系统概述系统调用(一)什么是系统调用,有何作用(二)系统调用与库函数的区别(三)小例子:为什么系统调用是必须的(四)什么功能要用到系统调…...

Vue基础学习 第一个Vue程序 el挂载点 v-指令(1)
Vue简介 Vue是一个Javascript框架Vue框架可以简化Dom操作响应式数据驱动 : 页面是由数据生成的,当数据出现改动,页面也会即时改变 第一个Vue程序 Vue中文文档官网:https://v2.cn.vuejs.org/v2/guide/ 根据官方文档的说法&#…...

前端页面性能
提升页面性能的方法资源压缩合并,减少HTTP请求非核心代码异步加载异步加载方式?1)动态脚本加载、2)defer、3)async(在加载js的时候在script标签上添加这两个属性,<script src"./test.js" charset"utf-8" defer><…...

2023-03-04 反思
摘要: 当前的时期确实比较特殊,不但是对于一个生命周期的最后的挣扎,更是在经历了各种浮浮沉沉的波澜之后还有更多的波浪。 精神分析-GRY: 非常奇怪的一个跳梁小丑, 不过我个人认为用这个标签是对跳梁小丑的侮辱和上层管理者对于这种人的纵容有很大关系…...

奇思妙想:超链接唤起本地应用
文章目录分析实现参考很多人的博客都有这样的小玩意,点击之后就可以直接与博主进行对话,而且无需添加好友。 先研究一下网页源代码: <a href"tencent://message/?uin88888888&Siteqq&Menuyes">联系我</a>很明…...

初识数据结构——“数据结构与算法”
各位CSDN的uu们你们好呀,今天小雅兰进入一个全新的内容的学习,就是算法和数据结构啦,话不多说,让我们进入数据结构的世界吧 什么是数据结构? 什么是算法? 数据结构和算法的重要性 如何学好数据结构和算…...

华为OD机试Golang解题 - 计算网络信号
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

ESP32编译及运行错误记录
1、打印格式不对 一般都是因为日志中某个参数打印格式不匹配造成。 ESP_LOGI(TAG, "[APP] Free memory: %lu bytes", esp_get_free_heap_size());//将之前的%d 改为%lu 2、配置载不对 这里选择了蓝牙模块需要引入蓝牙组件才能编译通过 idf.py menuconfig Component…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
