初识数据结构——“数据结构与算法”
各位CSDN的uu们你们好呀,今天小雅兰进入一个全新的内容的学习,就是算法和数据结构啦,话不多说,让我们进入数据结构的世界吧
什么是数据结构?
什么是算法?
数据结构和算法的重要性
如何学好数据结构和算法
算法的时间复杂度和空间复杂度
算法效率
时间复杂度
空间复杂度
常见复杂度对比
复杂度的oj练习
什么是数据结构?
数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的 数据元素的集合。
实现一些项目,需要在内存中将数据存储起来,比如实现一个通讯录,把每个人的信息存储起来,可以使用数组的方式,也可以使用链表,当然,也可以使用树
什么是算法?
算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
排序、查找、去重
数据结构和算法的重要性
- 怎么计算一个类到底实例化了多少对象?
- 如果还有一个派生类继承了这个类,那么如何计算这两个类,各自实例化了多少对象?
- 你了解联合体和结构体吗?
- 如何测试一个机器是大端还是小端?
- 你了解队列和栈吗?
- 怎么用两个栈实现一个队列。
- 你使用过模版吗?
- 写一个比较两个数大小的模板函数。
- 你使用过容器吗?
- 判断两个链表是否相交。
- Vector和数组的区别。
- 你在学校里做的最满意的一个项目是什么?简述一下这个项目。
- 自我介绍
- 学习STL具体是怎么开展的?
- 如果一款产品给你怎么检测内存泄露?
- 进程间通信方式,共享内存是怎么实现的,会出现什么问题,怎么解决?
- TCP为什么是可靠的?可靠是怎么保证的?为什么要三次握手?为什么三次握手就可以可靠?
- Http数据分包问题;
- Vector相关;
- Hashmap相关;
- 红黑树的原理、时间复杂度等;
- Memcpy和memmove的区别;
- 客户端给服务器发送数据,意图发送aaa,然后再发bbb,但是可能会出现aaabbb这种情 况,如何处理?
- 游戏的邮件服务器中每天会有玩家频繁的创建邮件和删除邮件,海量数据、大小不一,会有 哪些场景,怎么存储,邮件是怎么到内存的?
- 写一道算法题
- 手写五道题,三道编程题,一道数据库,一道linux
- 数据库的题两问
- 算法了解的如何,插入排序编程
- 说一下IP,TCP,ARP
- 内核是什么
- IP层主要功能
- map和set底层
- bootstrap的用法,html,html的全称
- 你觉得框架和库有啥区别
- 代码优化
- 哈希表
- shell脚本
- 快速排序思想
- 递归是什么
- 分治是什么,与递归区别是什么
- web平台是怎么做的
- linux命令
- 了解些什么前沿的技术,英语怎么样,了解过什么英语的文献
可见,数据结构与算法确实是非常重要的
如何学好数据结构和算法
死磕代码,磕成这样就可以了,哈哈哈

注意画图和思考
算法效率
算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
时间复杂度
时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一 个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
此函数表示数学里面带有未知数的函数表达式,和C语言的函数不一样
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。

下面,我们来看一个具体的例子:
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);}Func1 执行的基本操作次数:

- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010
N越大,后两项对结果的影响是越小的
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这 里我们使用大O的渐进表示法。
大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
下面,还是来先看看题目吧!!!
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
一般情况下时间复杂度计算时都是用的N,但是其他的,比如M、K也是可以的
如果题目有条件:
- M远大于N,那么可以认为是O(M)
- N远大于M,那么可以认为是O(N)
- M和N差不多大,那么可以认为是O(M),也可以认为是O(N)
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
基本操作执行了100次,通过推导大O阶方法,时间复杂度为 O(1)
O(1),不是代表算法运行一次,是常数次
// 计算strchr的时间复杂度?
const char* strchr(const char* str, int character);

有些算法的时间复杂度存在最好、平均和最坏情况:
- 最坏情况:任意输入规模的最大运行次数(上界)
- 平均情况:任意输入规模的期望运行次数
- 最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
- 最好情况:1次找到
- 最坏情况:N次找到
- 平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)

所以:
基本操作执行最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
基本操作执行最好N次,最坏执行了(N*(N+1)/2)次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N^2)
算时间复杂度不能只去看是几层循环,而是要看它的思想
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x){begin = mid + 1;}else if (a[mid] > x){end = mid - 1;}else{return mid;}}return -1;
}基本操作执行最好1次,最坏O(logN)次,时间复杂度为 O(logN)
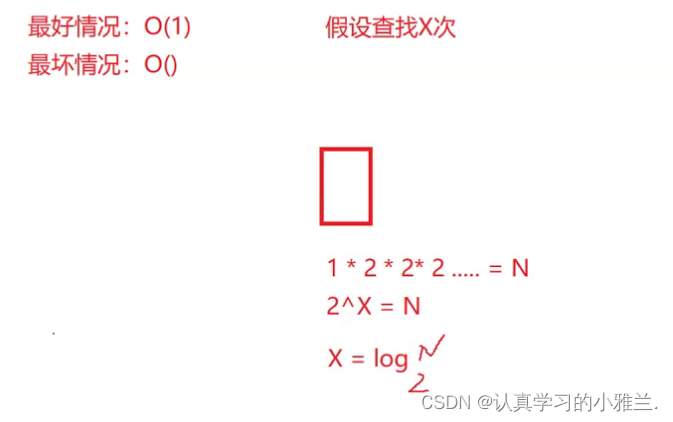
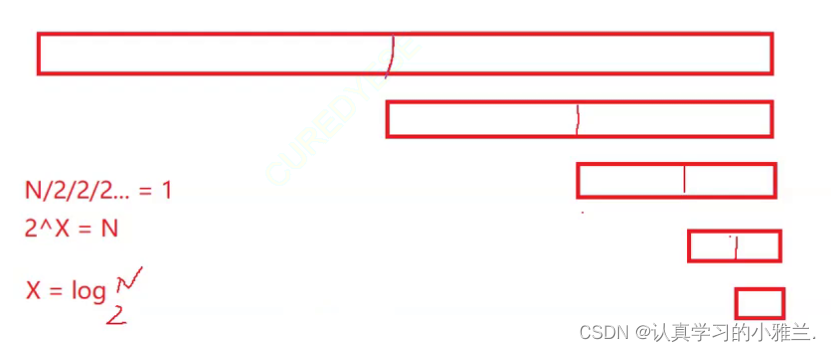
logN在算法分析中表示是底数为2,对数为N。有些地方会写成lgN。

// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}递归算法:递归次数*每次递归调用的次数
递归次数为O(1),每次递归调用的次数为O(N)
通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}通过计算分析发现基本操作递归了2^N次,时间复杂度为O(2^N)。
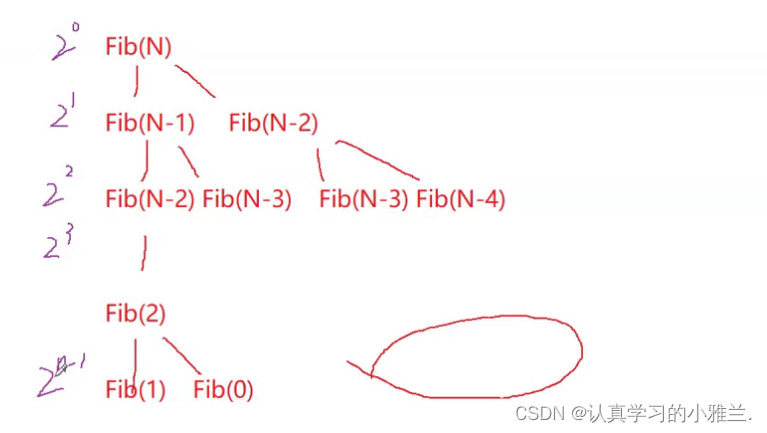
右边一些递归分支会提前结束,那么,就会缺一些递归调用,但是对总体来说影响不大

每次递归调用的次数是O(1)
斐波拉契数列的递归写法完全就是一个实际上没用的算法,因为太慢了
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时额外占用存储空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。 空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
下面,还是来看看题目:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
使用了常数个额外空间,所以空间复杂度为 O(1)
// 计算Fibonacci的空间复杂度?// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}动态开辟了N个空间,空间复杂度为 O(N)
时间复杂度:O(N)
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
- 空间是可以重复利用,不累计的
- 时间是一去不复返,累计的
常见复杂度对比
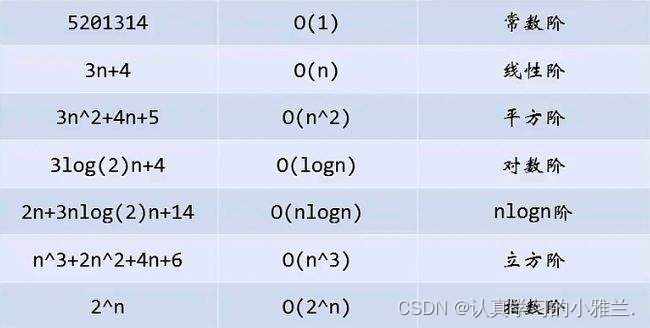
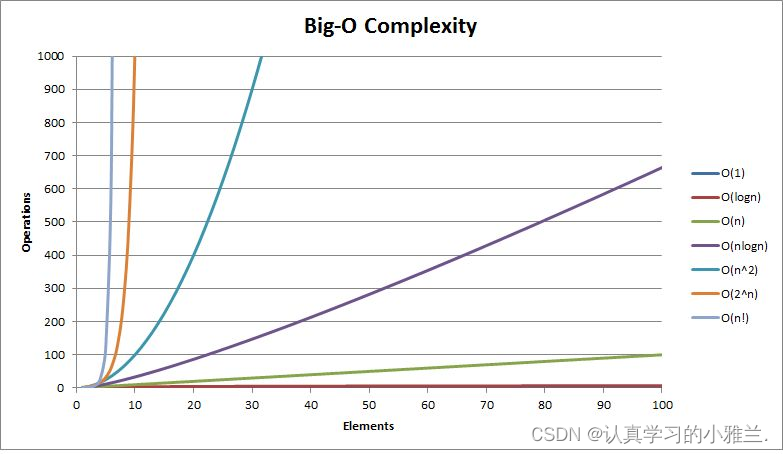
复杂度的oj练习
力扣
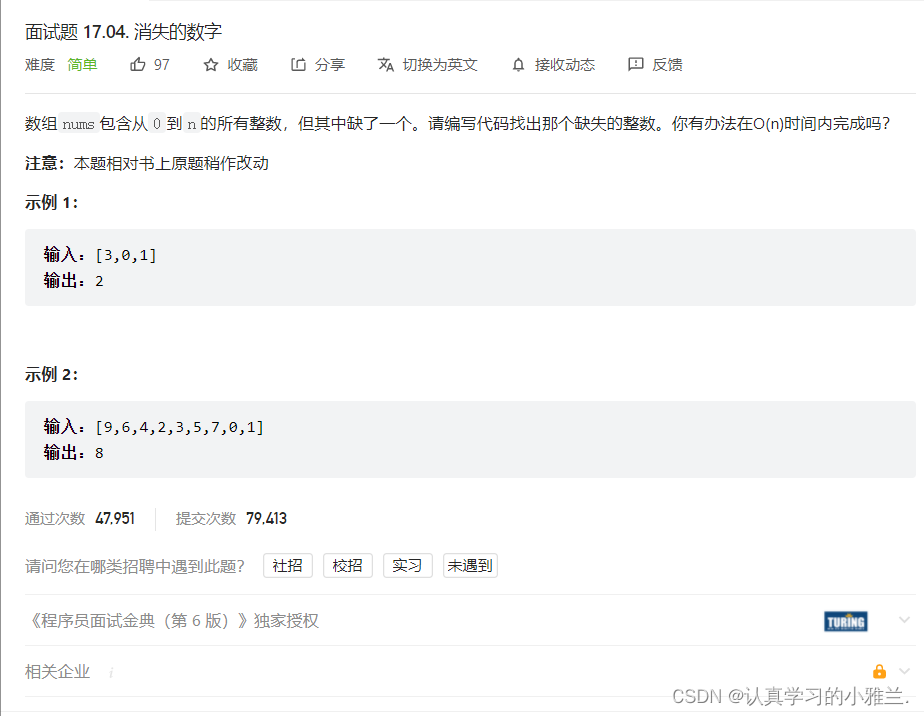


int missingNumber(int* nums, int numsSize)
{int x = 0;//跟[0,n]异或for (int i = 0; i <= numsSize; i++){x ^= i;}//再跟数组中值异或for (int i = 0; i < numsSize; i++){x ^= nums[i];}return x;
}好啦,小雅兰今天的内容就到这里啦,数据结构与算法确实是一个难啃的东西,小雅兰加油呀!!!

相关文章:

初识数据结构——“数据结构与算法”
各位CSDN的uu们你们好呀,今天小雅兰进入一个全新的内容的学习,就是算法和数据结构啦,话不多说,让我们进入数据结构的世界吧 什么是数据结构? 什么是算法? 数据结构和算法的重要性 如何学好数据结构和算…...

华为OD机试Golang解题 - 计算网络信号
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

ESP32编译及运行错误记录
1、打印格式不对 一般都是因为日志中某个参数打印格式不匹配造成。 ESP_LOGI(TAG, "[APP] Free memory: %lu bytes", esp_get_free_heap_size());//将之前的%d 改为%lu 2、配置载不对 这里选择了蓝牙模块需要引入蓝牙组件才能编译通过 idf.py menuconfig Component…...

GEE开发之降雨(CHIRPS)数据获取和分析
GEE开发之降雨CHIRPS数据获取和分析1.数据介绍2.初识CHIRPS2.1 代码一2.2 代码二3.逐日数据分析和获取4.逐月数据分析和获取4.1 代码一4.2 代码二(简洁)5.逐年数据分析和获取5.1 代码一5.2 代码二(简洁)前言:主要获取和分析UCSB-CHG/CHIRPS/DAILY的日数据、月数据和…...

TypeScript中面向对象
面向对象 要想面向对象,操作对象,首先便要拥有对象; 要创建对象,必须要先定义类,所谓的类可以理解为对象的模型; 程序中可以根据类创建指定类型的对象; 举例来说: 可以通过Perso…...

Transformer 模型:入门详解(1)
动动发财的小手,点个赞吧! 简介 众所周知,transformer 架构是自然语言处理 (NLP) 领域的一项突破。它克服了 seq-to-seq 模型(如 RNN 等)无法捕获文本中的长期依赖性的局限性。事实证明,transformer 架构是…...

深入理解js中的new关键字
在js中我们经常会使用到new关键字,那我们在使用new关键字的时候,new到底做了什么呢?今天我们就来深入探究一下 1.初步使用 我们先来使用一下,这是一个正常操作 function Person() {this.name "John";}let person new…...
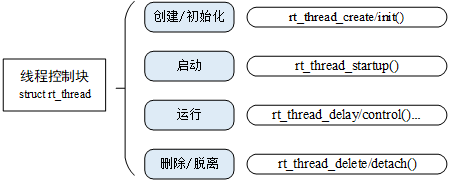
RT-Thread Nano(2) - 线程
参考:RT-Thread API参考手册: 线程管理 线程的分类:动态线程,静态线程 动态线程是系统自动从动态内存堆上分配栈空间的线程句柄(程序运行时再分配空间),静态线程是由用户分配栈空间与线程句柄(可以说是程序编译时已经分配好空间) 1.创建线程 创建一个动态线程 rt_thread_t …...
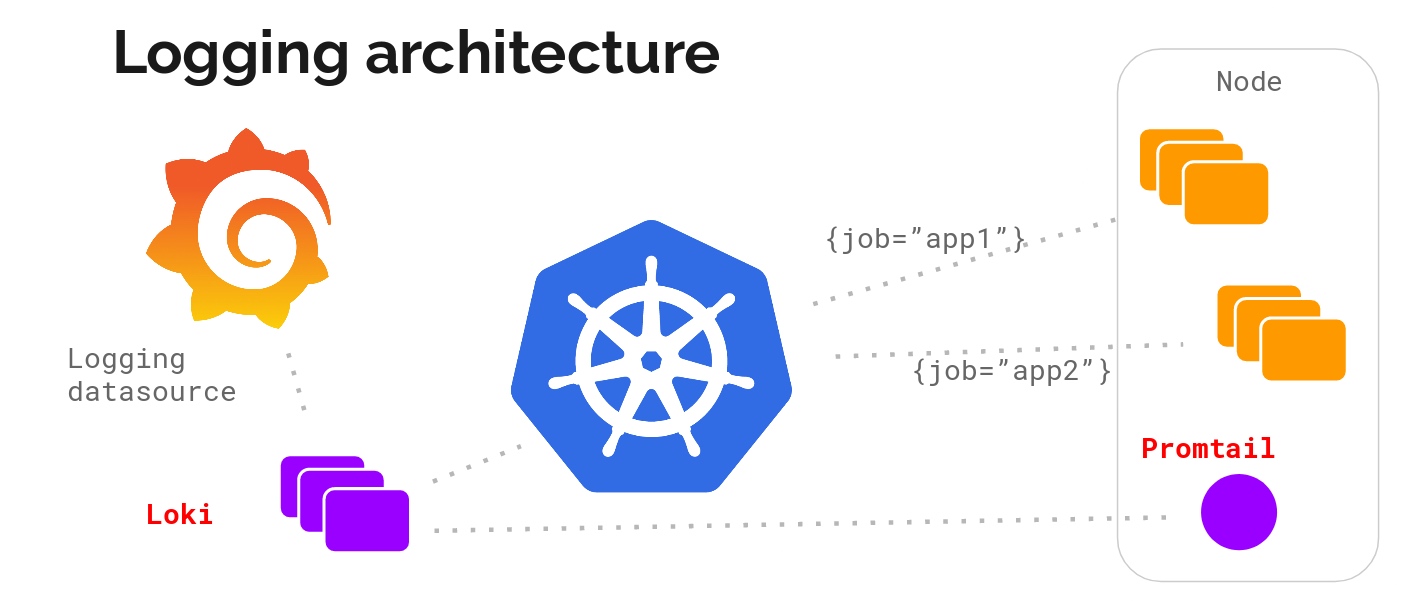
真香,Grafana开源Loki日志系统取代ELK?
一、Loki是什么? Loki是由Grafana Labs开源的一个水平可扩展、高可用性,多租户的日志聚合系统的日志聚合系统。它的设计初衷是为了解决在大规模分布式系统中,处理海量日志的问题。Loki采用了分布式的架构,并且与Prometheus、Graf…...

机器学习|多变量线性回归 | 吴恩达学习笔记
前文回顾:机器学习 | 线性回归(单变量) 目录 📚多维特征 📚多变量梯度下降 📚梯度下降法实践 🐇特征缩放 🐇学习率 📚特征和多项式回归 📚正规方程 &…...

高并发内存池
按照threadcache,centralcache,pagecache顺序所列 这里还需要一定的前期准备工作 首先是可以设计一个定长内存池 ObjectPool.h #pragma once #include<iostream> #include"Common.h" using std::cout; using std::endl; using std::…...

springboot mybatis-plus 对接 sqlserver 数据库 批处理的问题
问题: 在对接 sqlserver数据库的时候 主子表 保存的时候 子表批量保存 使用的 mybatis-plus提供的saveOrUpdateBatch 这个方法 但是 报错 报错内容为 : com.microsoft.sqlserver.jdbc.SQLServerException: 必须执行该语句才能获得结果。 框架版本 sprin…...
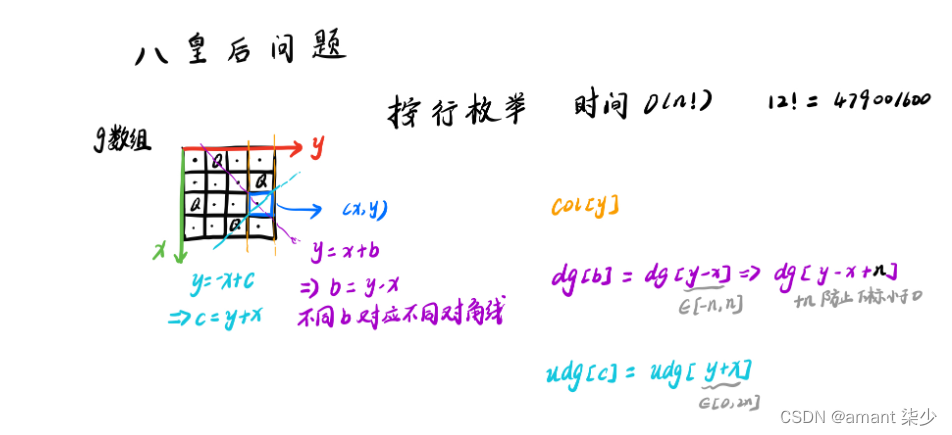
Acwing---843. n-皇后问题——DFS
n-皇后问题1.题目2.基本思想3.代码实现1.题目 n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 …...

Android事件分发机制
文章目录Android View事件分发机制:事件分发中的核心方法onTouchListener和onClickListener的优先级事件分发DOWN,MOVE,UP 事件分发CANCEL代码实践requestdisallowIntereptTouchEvent作用Android View事件分发机制: 事件分发中的核心方法 Android中事件…...

python版协同过滤算法图书管理系统
基于协同过滤算法的图书管理系统 一、简介(v信:1257309054) 本系统基于推荐算法给用户实现精准推荐图书。 根据用户对物品或者信息的偏好,发现物品或者内容本身的相关性,或者是发现用户的相关性,然…...
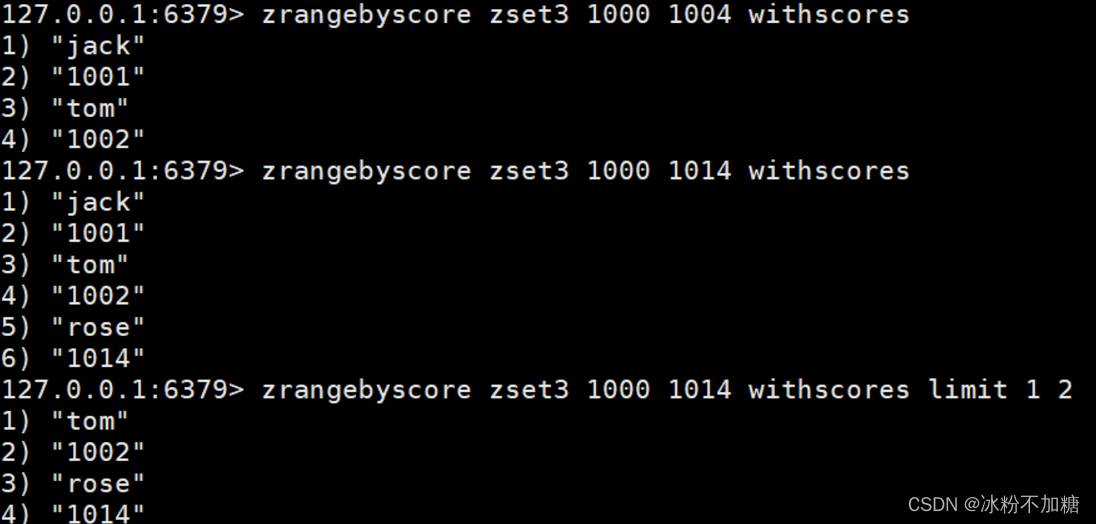
Redis基础入门
文章目录前言一、redis是什么?二、安装步骤1.下载安装包2.安装三、Redis的数据类型redis是一种高级的key-value的存储系统,其中的key是字符串类型,尽可能满足如下几点:字符串(String)列表(List)集合(Set,不允许出现重复…...

【微服务】Feign实现远程调用和负载均衡
目录 1.什么是Feign 2 订单微服务集成Feign 2.1.引入依赖 2.2添加注解 2.3编写Feign的客户端 2.4修改OrderServiceImpl.java的远程调用方法 2.5重启订单服务,并验证 总结 1.什么是Feign Feign是Spring Cloud提供的⼀个声明式的伪Http客户端, 它…...

Windows使用QEMU搭建arm64 ubuntu 环境
1. 下载 QEMU: https://qemu.weilnetz.de/w64/ QEMU UEFI固件文件: https://releases.linaro.org/components/kernel/uefi-linaro/latest/release/qemu64/QEMU_EFI.fd arm64 Ubuntu镜像: http://cdimage.ubuntu.com/releases/20.04.3/rel…...

NodeJS安装
一、简介Node.js是一个让JavaScript运行在服务端的开发平台,Node.js不是一种独立的语言,简单的说 Node.js 就是运行在服务端的 JavaScript。npm其实是Node.js的包管理工具(package manager),类似与 maven。二、安装步骤…...

Gin 优雅打印请求与回包内容
文章目录1.Gin 的 Middleware2.使用 Middleware 打印请求与回包内容3.多次读取请求 Body 的问题4.多次读取响应 Body 的问题5.小结参考文献在开发 Web 应用程序时,难免不会遇到功能或性能等问题。为了快速定位问题,需要打印请求和响应的内容。本文将介绍…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
