深入理解js中的new关键字
在js中我们经常会使用到new关键字,那我们在使用new关键字的时候,new到底做了什么呢?今天我们就来深入探究一下
1.初步使用
我们先来使用一下,这是一个正常操作
function Person() {this.name = "John";}let person = new Person();console.log(person.name); // Johnnew关键字主要做了这几件事情:
1.创建一个新对象
2.将构造函数的作用域赋值给新对象(this指向新对象)
3.执行构造函数中的代码
4.返回新对象
2.不使用new
那我们不使用new关键字,又会发生什么?
function Person1() {this.name = "John1";}let p1 = Person1();console.log(p1); //undefinedconsole.log(name); //name this指向window,所以输出John13.构造函数有return
function Person2() {this.name = "mike";return { age: 18 };}let p2 = new Person2();console.log(p2); //{age: 18}console.log(p2.name); //undefined如果构造函数返回一个对象,new命令会直接返回这个return的对象
如果return的不是一个对象,那还是回按照new的实现步骤,返回实例对象
4.手动实现new关键字
function _new(fn, ...args) {if (typeof fn !== "function") {throw "fn must be a function";}// 创建一个对象,其对象的原型,指向构造函数的原型对象let obj = Object.create(fn.prototype);let res = fn.apply(obj, ...args);return res instanceof Object ? res : obj// 构造函数本身如果返回的是对象的话,则 返回的就是此对象// 如果返回值不是对象的话,则 返回对应的objreturn isObject || isFunction ? res : obj;}function Ele() {this.name = "Ele";}let e = _new(Ele)console.log(e.name); // Ele如果你觉得本文对你有所帮助,欢迎评论,点赞与关注,一起卷~
相关文章:

深入理解js中的new关键字
在js中我们经常会使用到new关键字,那我们在使用new关键字的时候,new到底做了什么呢?今天我们就来深入探究一下 1.初步使用 我们先来使用一下,这是一个正常操作 function Person() {this.name "John";}let person new…...
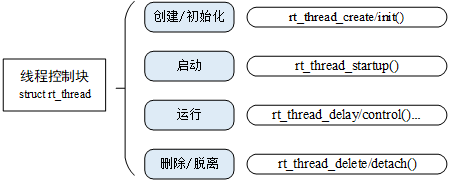
RT-Thread Nano(2) - 线程
参考:RT-Thread API参考手册: 线程管理 线程的分类:动态线程,静态线程 动态线程是系统自动从动态内存堆上分配栈空间的线程句柄(程序运行时再分配空间),静态线程是由用户分配栈空间与线程句柄(可以说是程序编译时已经分配好空间) 1.创建线程 创建一个动态线程 rt_thread_t …...
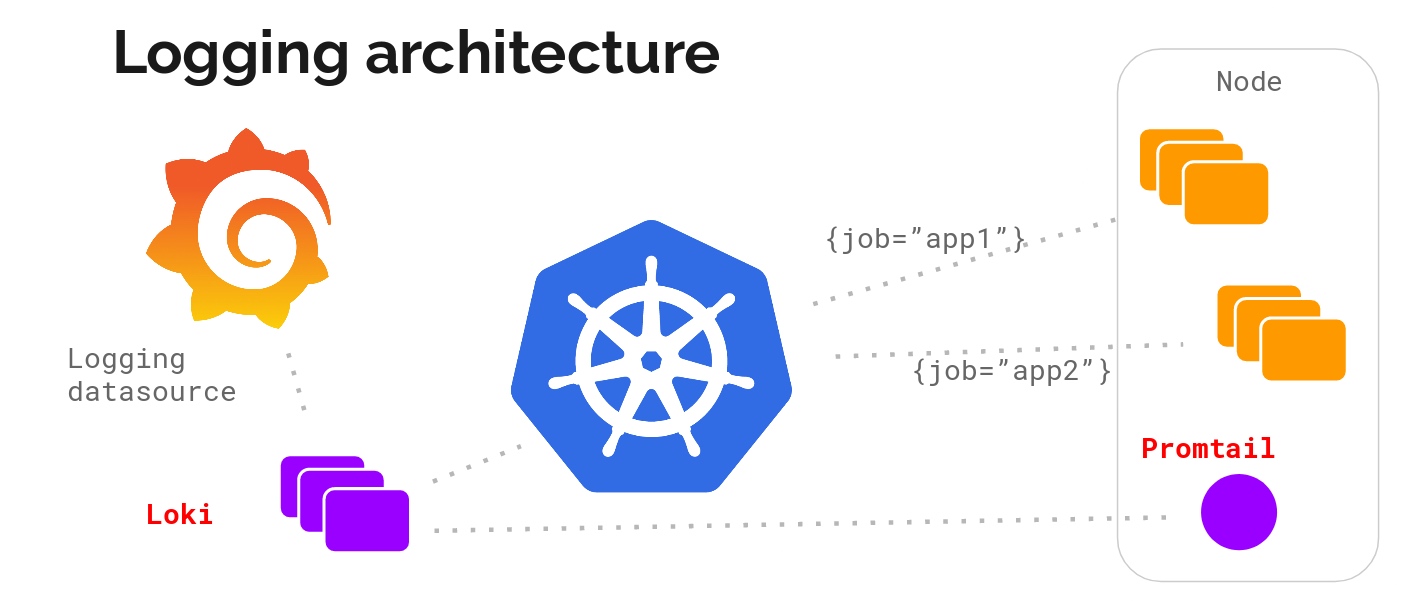
真香,Grafana开源Loki日志系统取代ELK?
一、Loki是什么? Loki是由Grafana Labs开源的一个水平可扩展、高可用性,多租户的日志聚合系统的日志聚合系统。它的设计初衷是为了解决在大规模分布式系统中,处理海量日志的问题。Loki采用了分布式的架构,并且与Prometheus、Graf…...

机器学习|多变量线性回归 | 吴恩达学习笔记
前文回顾:机器学习 | 线性回归(单变量) 目录 📚多维特征 📚多变量梯度下降 📚梯度下降法实践 🐇特征缩放 🐇学习率 📚特征和多项式回归 📚正规方程 &…...

高并发内存池
按照threadcache,centralcache,pagecache顺序所列 这里还需要一定的前期准备工作 首先是可以设计一个定长内存池 ObjectPool.h #pragma once #include<iostream> #include"Common.h" using std::cout; using std::endl; using std::…...

springboot mybatis-plus 对接 sqlserver 数据库 批处理的问题
问题: 在对接 sqlserver数据库的时候 主子表 保存的时候 子表批量保存 使用的 mybatis-plus提供的saveOrUpdateBatch 这个方法 但是 报错 报错内容为 : com.microsoft.sqlserver.jdbc.SQLServerException: 必须执行该语句才能获得结果。 框架版本 sprin…...
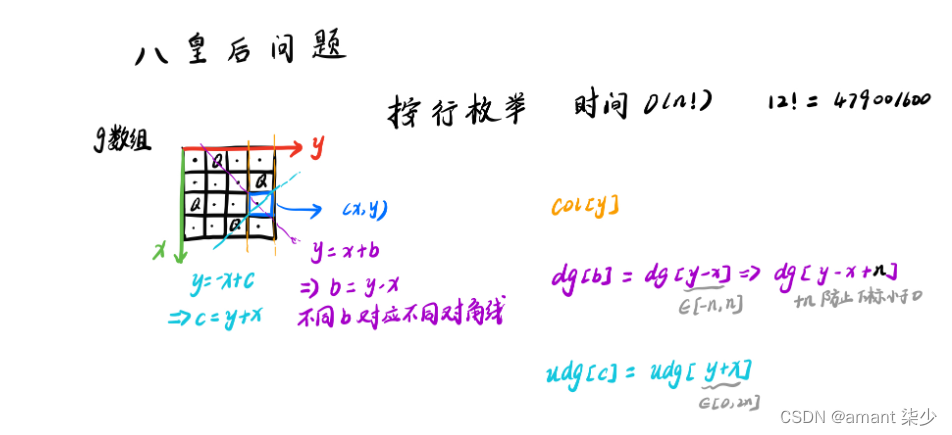
Acwing---843. n-皇后问题——DFS
n-皇后问题1.题目2.基本思想3.代码实现1.题目 n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 …...

Android事件分发机制
文章目录Android View事件分发机制:事件分发中的核心方法onTouchListener和onClickListener的优先级事件分发DOWN,MOVE,UP 事件分发CANCEL代码实践requestdisallowIntereptTouchEvent作用Android View事件分发机制: 事件分发中的核心方法 Android中事件…...

python版协同过滤算法图书管理系统
基于协同过滤算法的图书管理系统 一、简介(v信:1257309054) 本系统基于推荐算法给用户实现精准推荐图书。 根据用户对物品或者信息的偏好,发现物品或者内容本身的相关性,或者是发现用户的相关性,然…...
Redis基础入门
文章目录前言一、redis是什么?二、安装步骤1.下载安装包2.安装三、Redis的数据类型redis是一种高级的key-value的存储系统,其中的key是字符串类型,尽可能满足如下几点:字符串(String)列表(List)集合(Set,不允许出现重复…...

【微服务】Feign实现远程调用和负载均衡
目录 1.什么是Feign 2 订单微服务集成Feign 2.1.引入依赖 2.2添加注解 2.3编写Feign的客户端 2.4修改OrderServiceImpl.java的远程调用方法 2.5重启订单服务,并验证 总结 1.什么是Feign Feign是Spring Cloud提供的⼀个声明式的伪Http客户端, 它…...

Windows使用QEMU搭建arm64 ubuntu 环境
1. 下载 QEMU: https://qemu.weilnetz.de/w64/ QEMU UEFI固件文件: https://releases.linaro.org/components/kernel/uefi-linaro/latest/release/qemu64/QEMU_EFI.fd arm64 Ubuntu镜像: http://cdimage.ubuntu.com/releases/20.04.3/rel…...

NodeJS安装
一、简介Node.js是一个让JavaScript运行在服务端的开发平台,Node.js不是一种独立的语言,简单的说 Node.js 就是运行在服务端的 JavaScript。npm其实是Node.js的包管理工具(package manager),类似与 maven。二、安装步骤…...

Gin 优雅打印请求与回包内容
文章目录1.Gin 的 Middleware2.使用 Middleware 打印请求与回包内容3.多次读取请求 Body 的问题4.多次读取响应 Body 的问题5.小结参考文献在开发 Web 应用程序时,难免不会遇到功能或性能等问题。为了快速定位问题,需要打印请求和响应的内容。本文将介绍…...

关于k8s中ETCD集群备份灾难恢复的一些笔记
写在前面 集群电源不稳定,或者节点动不动就 宕机,一定要做好备份,ETCD 的快照文件很容易受影响损坏。重置了很多次集群,才认识到备份的重要博文内容涉及 etcd 运维基础知识了解静态 Pod 方式 etcd 集群灾备与恢复 Demo定时备份的任务编写二进…...

【设计模式之美 设计原则与思想:设计原则】19 | 理论五:控制反转、依赖反转、依赖注入,这三者有何区别和联系?
关于 SOLID 原则,我们已经学过单一职责、开闭、里式替换、接口隔离这四个原则。今天,我们再来学习最后一个原则:依赖反转原则。在前面几节课中,我们讲到,单一职责原则和开闭原则的原理比较简单,但是&#x…...

2023年全国最新高校辅导员精选真题及答案13
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、单选题 131.下列不属于我国国土空间具有的特点的是() A.水资…...

【XXL-JOB】XXL-JOB定时处理视频转码
【XXL-JOB】XXL-JOB定时处理视频转码 文章目录【XXL-JOB】XXL-JOB定时处理视频转码1. 准备工作1.1 高级配置1.2 分片广播2. 需求分析2.1 作业分片方案2.2 保证任务不重复执行2.2.1 保证幂等性3. 视频处理业务流程3.1 添加待处理任务3.2 查询待处理任务3.3 更新任务状态3.4 工具…...

optuna用于pytorch的轻量级调参场景和grid search的自定义设计
文章目录0. 背景:why optuna0.1 插播一个简单的grid search0.2 参考1. Optuna1.1 a basic demo与部分参数释义1.2 random的问题1.3 Objective方法类2. Optuna与grid search4. optuna的剪枝prune5. optuna与可视化6. 未完待续0. 背景:why optuna 小模型参…...

语法篇--汇编语言先导浅尝
一、相关概念 1.机器语言 机器语言(Machine Language)是一种计算机程序语言,由二进制代码(0和1)组成,可被计算机直接执行。机器语言是计算机硬件能够理解和执行的唯一语言。 机器语言通常由一系列的指令组…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
