机器学习|多变量线性回归 | 吴恩达学习笔记
前文回顾:机器学习 | 线性回归(单变量)
目录
📚多维特征
📚多变量梯度下降
📚梯度下降法实践
🐇特征缩放
🐇学习率
📚特征和多项式回归
📚正规方程
📚梯度下降与正规方程的比较
📚多维特征
接上文单变量线性回归,现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为
。
增添更多特征后,我们引入一系列新的注释:
-
代表特征的数量
代表第i个训练实例,是特征矩阵中的第i行,是一个向量。
代表特征矩阵中第i行的第j个特征,也就是第i个训练实例的第j个特征。

- 支持多变量的假设h表示为:
,这个公式中有n+1个参数和n个变量,为了使公式能够简化一些,引入
。
- 则公式转化为
- 此时模型中的参数是一个n+1维的向量,任何一个训练实例也都是n+1维的向量,最后公式可以简化为:

- 则公式转化为
📚多变量梯度下降
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,且我们的目标依旧是要找出使得代价函数最小的一系列参数。

多元线性回归的批量梯度下降算法为:


在这里我们回顾当时单变量用到的代价函数,就会发现单变量多变量的代价函数其实就是同一个东西,
。
我们开始随机选择一系列参数值,计算所有的预测结果后,再给所有的参数一个新的值,如此循环直至收敛。
📚梯度下降法实践
🐇特征缩放
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000 平方英尺,而房间数量的值则是 0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,图像会显得很扁,梯度下降算法需要非常多次的迭代(会反复振荡)才能收敛,就是会走一条折来折去的路线来找全局最小值。

最简单的方法是令:,其中
是平均值,
是标准差。针对这个
,一般就是最大值减去最小值就可以了。而且其实特征缩放也不一定需要那么精确,我们只是为了让梯度下降运行得更快一点,收敛所需的迭代次数更少。
🐇学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,而我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

所以这条曲线显示的是梯度下降的每步迭代后代价函数的值。如果代价函数正常工作的话,每一步迭代之后都应该下降,因此看这种曲线图可以告诉你算法有没有正常工作。而且可以通过这个曲线判断梯度下降算法最后有没有收敛(如上图,可以判断在400次左右就已经收敛了)。
也有一些自动测试是否收敛的方法,例如将代价函数的变化值与某个阀值(例如 0.001)进行比较,但通常看上面这样的图表更好。
通常可以考虑尝试这些学习率:,通过图像找出最快收敛的
。
📚特征和多项式回归
如以下房价预测问题,所给的特征是邻街宽度和纵向深度,而我们可以用临街宽度×纵向深度得到面积,并用面积这一更好的特征来替换原有的那两个特征。
与选择特征想法密切相关的一个概念被称为多项式回归。
线性回归并不适用于所有的数据,有时我们需要曲线来适应我们的数据,例如以下所给出的数据集,我们或许会用二次方模型去拟合(考虑到数据集的后续下降趋势),也可以用三次方模型去拟合(考虑到数据集后续再升高),通常我们需要先观察数据然后再决定准备尝试怎样的模型。

且相关特征的选择也可以是灵活的,例如以下二次方模型的两种特征选择。

最后不管选择了怎样的模型,我们可以通过换元在将模型转化为线性回归模型。

注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。因为平方甚至更高次方等等数据之间相差太多啦。
📚正规方程
到目前为止,我们都在使用梯度下降算法,但是对于某些线性回归问题,正规方法是更好的解决方案。正规方程(区别于迭代方法的直接解法)。
假设我们的训练集特征矩阵为X(包含了),并且我们的训练集结果为向量y,则利用正规方程解出向量

在Octave中,正规方程写作:
pinv(X'*X)*X'*y注:
- 对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),正规方程方法是不能用的(原则上)。
- 首先,看特征值里是否有一些多余的特征,像这些
和
是线性相关的,互为线性函数。同时,当有一些多余的特征时,可以删除这两个重复特征里的其中一个,无须两个特征同时保留,将解决不可逆性的问题。
- 但于𝑋′𝑋的不可逆的问题很少发生,在 Octave 里,如果用pinv()来实现𝜃的计算,会得到一个正常的解,即便矩阵 𝑋′𝑋是不可逆的(即使𝑋′𝑋的结果是不可逆的,但算法执行的流程是正确的)。在 Octave 里,有两个函数可以求解矩阵的逆,一个被称为 pinv(),另一个是 inv(),这两者之间的差异是些许计算过程上的,一个是所谓的伪逆, 另一个被称为逆。
是不可逆的。
📚梯度下降与正规方程的比较
| 梯度下降 | 正规方程 |
| 需要选择学习率 | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量n大时也能较好适用 | 需要计算 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
一般来说,只要特征变量的数目并不大,标准方程是一个很好的计算参数θ的替代方法。
参考学习链接:【中英字幕】吴恩达机器学习系列课程,本篇对应4.1-4.7
be happy——

相关文章:

机器学习|多变量线性回归 | 吴恩达学习笔记
前文回顾:机器学习 | 线性回归(单变量) 目录 📚多维特征 📚多变量梯度下降 📚梯度下降法实践 🐇特征缩放 🐇学习率 📚特征和多项式回归 📚正规方程 &…...

高并发内存池
按照threadcache,centralcache,pagecache顺序所列 这里还需要一定的前期准备工作 首先是可以设计一个定长内存池 ObjectPool.h #pragma once #include<iostream> #include"Common.h" using std::cout; using std::endl; using std::…...

springboot mybatis-plus 对接 sqlserver 数据库 批处理的问题
问题: 在对接 sqlserver数据库的时候 主子表 保存的时候 子表批量保存 使用的 mybatis-plus提供的saveOrUpdateBatch 这个方法 但是 报错 报错内容为 : com.microsoft.sqlserver.jdbc.SQLServerException: 必须执行该语句才能获得结果。 框架版本 sprin…...
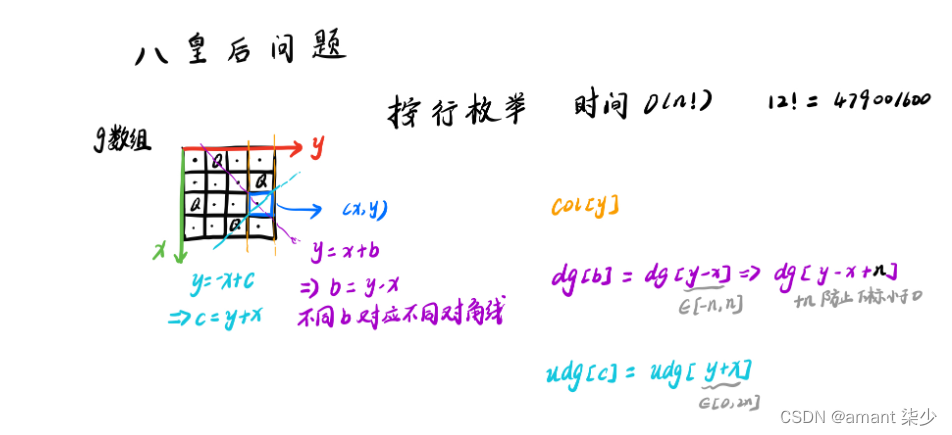
Acwing---843. n-皇后问题——DFS
n-皇后问题1.题目2.基本思想3.代码实现1.题目 n−皇后问题是指将 n 个皇后放在 nn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 n,请你输出所有的满足条件的棋子摆法。 …...

Android事件分发机制
文章目录Android View事件分发机制:事件分发中的核心方法onTouchListener和onClickListener的优先级事件分发DOWN,MOVE,UP 事件分发CANCEL代码实践requestdisallowIntereptTouchEvent作用Android View事件分发机制: 事件分发中的核心方法 Android中事件…...

python版协同过滤算法图书管理系统
基于协同过滤算法的图书管理系统 一、简介(v信:1257309054) 本系统基于推荐算法给用户实现精准推荐图书。 根据用户对物品或者信息的偏好,发现物品或者内容本身的相关性,或者是发现用户的相关性,然…...
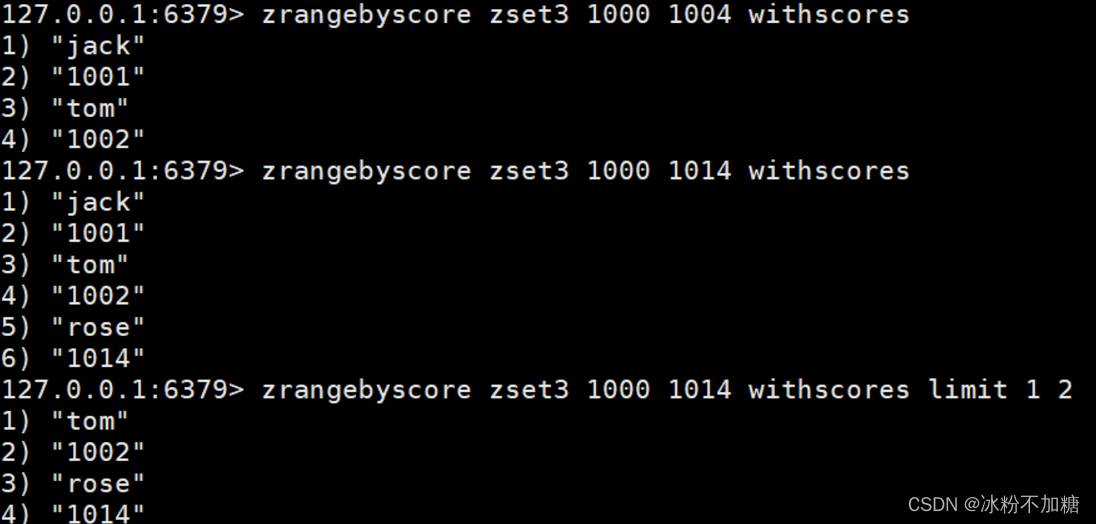
Redis基础入门
文章目录前言一、redis是什么?二、安装步骤1.下载安装包2.安装三、Redis的数据类型redis是一种高级的key-value的存储系统,其中的key是字符串类型,尽可能满足如下几点:字符串(String)列表(List)集合(Set,不允许出现重复…...

【微服务】Feign实现远程调用和负载均衡
目录 1.什么是Feign 2 订单微服务集成Feign 2.1.引入依赖 2.2添加注解 2.3编写Feign的客户端 2.4修改OrderServiceImpl.java的远程调用方法 2.5重启订单服务,并验证 总结 1.什么是Feign Feign是Spring Cloud提供的⼀个声明式的伪Http客户端, 它…...

Windows使用QEMU搭建arm64 ubuntu 环境
1. 下载 QEMU: https://qemu.weilnetz.de/w64/ QEMU UEFI固件文件: https://releases.linaro.org/components/kernel/uefi-linaro/latest/release/qemu64/QEMU_EFI.fd arm64 Ubuntu镜像: http://cdimage.ubuntu.com/releases/20.04.3/rel…...

NodeJS安装
一、简介Node.js是一个让JavaScript运行在服务端的开发平台,Node.js不是一种独立的语言,简单的说 Node.js 就是运行在服务端的 JavaScript。npm其实是Node.js的包管理工具(package manager),类似与 maven。二、安装步骤…...

Gin 优雅打印请求与回包内容
文章目录1.Gin 的 Middleware2.使用 Middleware 打印请求与回包内容3.多次读取请求 Body 的问题4.多次读取响应 Body 的问题5.小结参考文献在开发 Web 应用程序时,难免不会遇到功能或性能等问题。为了快速定位问题,需要打印请求和响应的内容。本文将介绍…...

关于k8s中ETCD集群备份灾难恢复的一些笔记
写在前面 集群电源不稳定,或者节点动不动就 宕机,一定要做好备份,ETCD 的快照文件很容易受影响损坏。重置了很多次集群,才认识到备份的重要博文内容涉及 etcd 运维基础知识了解静态 Pod 方式 etcd 集群灾备与恢复 Demo定时备份的任务编写二进…...

【设计模式之美 设计原则与思想:设计原则】19 | 理论五:控制反转、依赖反转、依赖注入,这三者有何区别和联系?
关于 SOLID 原则,我们已经学过单一职责、开闭、里式替换、接口隔离这四个原则。今天,我们再来学习最后一个原则:依赖反转原则。在前面几节课中,我们讲到,单一职责原则和开闭原则的原理比较简单,但是&#x…...

2023年全国最新高校辅导员精选真题及答案13
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、单选题 131.下列不属于我国国土空间具有的特点的是() A.水资…...

【XXL-JOB】XXL-JOB定时处理视频转码
【XXL-JOB】XXL-JOB定时处理视频转码 文章目录【XXL-JOB】XXL-JOB定时处理视频转码1. 准备工作1.1 高级配置1.2 分片广播2. 需求分析2.1 作业分片方案2.2 保证任务不重复执行2.2.1 保证幂等性3. 视频处理业务流程3.1 添加待处理任务3.2 查询待处理任务3.3 更新任务状态3.4 工具…...

optuna用于pytorch的轻量级调参场景和grid search的自定义设计
文章目录0. 背景:why optuna0.1 插播一个简单的grid search0.2 参考1. Optuna1.1 a basic demo与部分参数释义1.2 random的问题1.3 Objective方法类2. Optuna与grid search4. optuna的剪枝prune5. optuna与可视化6. 未完待续0. 背景:why optuna 小模型参…...

语法篇--汇编语言先导浅尝
一、相关概念 1.机器语言 机器语言(Machine Language)是一种计算机程序语言,由二进制代码(0和1)组成,可被计算机直接执行。机器语言是计算机硬件能够理解和执行的唯一语言。 机器语言通常由一系列的指令组…...

【ID:17】【20分】A. DS顺序表--类实现
时间限制1秒内存限制128兆字节题目描述用C语言和类实现顺序表属性包括:数组、实际长度、最大长度(设定为1000)操作包括:创建、插入、删除、查找类定义参考输入第1行先输入n表示有n个数据,即n是实际长度;接着输入n个数据…...
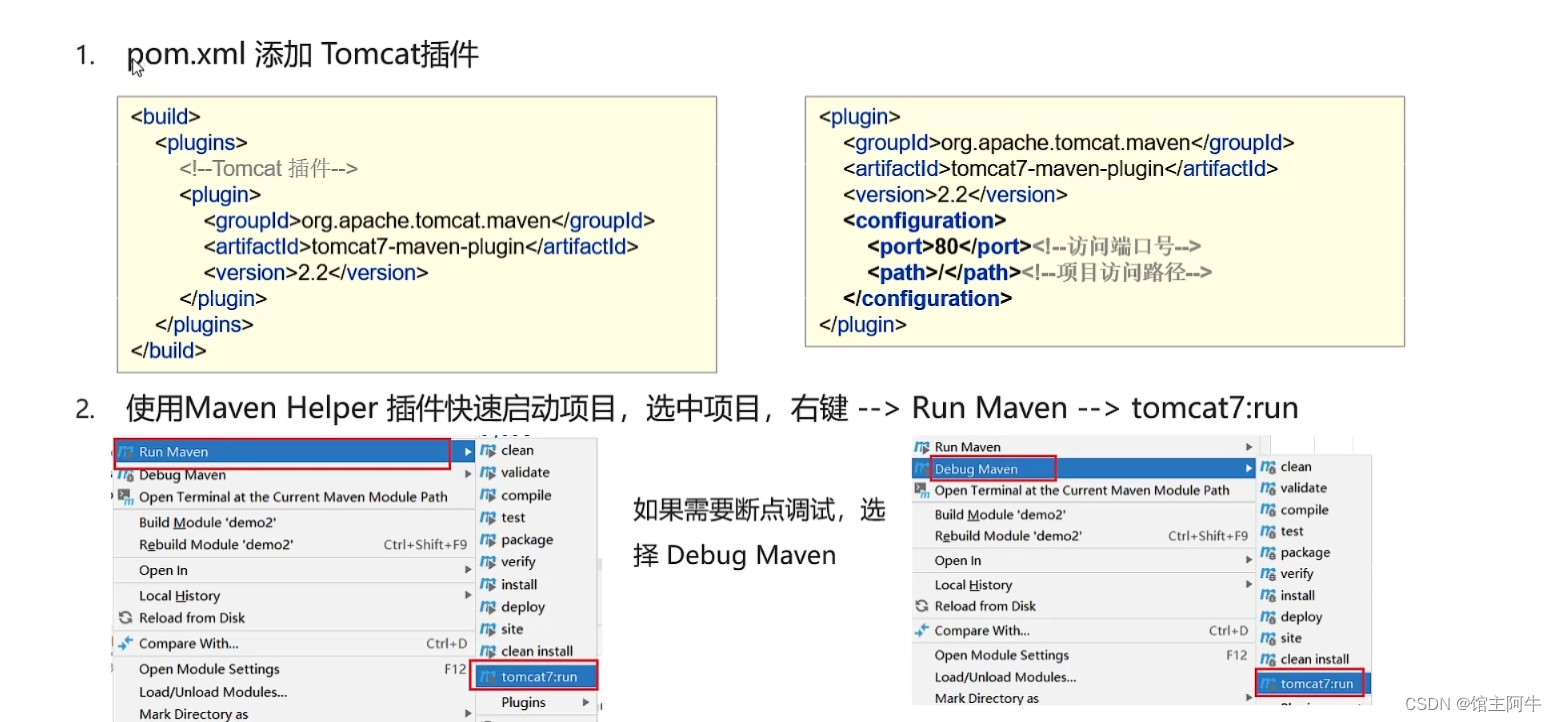
【java web篇】Tomcat的基本使用
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...

MySQL实战解析底层---行锁功过:怎么减少行锁对性能的影响
目录 前言 从两阶段锁说起 死锁和死锁检测 前言 MySQL 的行锁是在引擎层由各个引擎自己实现的但并不是所有的引擎都支持行锁,比如MyISAM 引擎就不支持行锁不支持行锁意味着并发控制只能使用表锁,对于这种引擎的表,同一张表上任何时刻只能有…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...



