ZJOI2009 对称的正方形
P2601 [ZJOI2009] 对称的正方形
题目大意
给定一个 n × m n\times m n×m的矩阵,求这个矩阵中满足上下对称且左右对称的正方形子矩阵的个数。
1 ≤ n , m ≤ 1000 1\leq n,m\leq 1000 1≤n,m≤1000
题解
首先,我们对原矩阵、左右翻转后的矩阵、上下翻转后的矩阵分别做二维哈希的处理。
对于边长为偶数的正方形,枚举正方形中心的格点并二分最远的符合题意的长度。
对于边长为奇数的正方形,枚举正方形中心的各自并二分最远的符合题意的长度。
判断是否符合题意可以通过判断三个矩阵中对应位置的二维哈希值是否相等来得到。
最后记得加上单个格子的贡献。
时间复杂度为 O ( n m log min ( n , m ) ) O(nm\log \min(n,m)) O(nmlogmin(n,m))。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1000;
const int bs1=131,bs2=233;
const long long mod=1e9+7;
int n,m,a[N+5][N+5],b[N+5][N+5],c[N+5][N+5];
long long ans=0,f1[N+5],f2[N+5];
long long s1[N+5][N+5],s2[N+5][N+5],s3[N+5][N+5];
long long gt1(int ux,int uy,int dx,int dy){return s1[dx][dy]-s1[dx][uy-1]*f1[dy-uy+1]%mod-s1[ux-1][dy]*f2[dx-ux+1]%mod+s1[ux-1][uy-1]*f1[dy-uy+1]%mod*f2[dx-ux+1]%mod;
}
long long gt2(int ux,int uy,int dx,int dy){return s2[dx][dy]-s2[dx][uy-1]*f1[dy-uy+1]%mod-s2[ux-1][dy]*f2[dx-ux+1]%mod+s2[ux-1][uy-1]*f1[dy-uy+1]%mod*f2[dx-ux+1]%mod;
}
long long gt3(int ux,int uy,int dx,int dy){return s3[dx][dy]-s3[dx][uy-1]*f1[dy-uy+1]%mod-s3[ux-1][dy]*f2[dx-ux+1]%mod+s3[ux-1][uy-1]*f1[dy-uy+1]%mod*f2[dx-ux+1]%mod;
}
bool check(int ux,int uy,int dx,int dy){if(ux<1||uy<1||dx>n||dy>m) return 0;long long v1,v2,v3;v1=(gt1(ux,uy,dx,dy)%mod+mod)%mod;v2=(gt2(n-dx+1,uy,n-ux+1,dy)%mod+mod)%mod;v3=(gt3(ux,m-dy+1,dx,m-uy+1)%mod+mod)%mod;return v1==v2&&v2==v3;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);b[n-i+1][j]=a[i][j];c[i][m-j+1]=a[i][j];}}f1[0]=f2[0]=1;for(int i=1;i<=min(n,m);i++){f1[i]=f1[i-1]*bs1%mod;f2[i]=f2[i-1]*bs2%mod;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){s1[i][j]=(s1[i][j-1]*bs1+a[i][j])%mod;s2[i][j]=(s2[i][j-1]*bs1+b[i][j])%mod;s3[i][j]=(s3[i][j-1]*bs1+c[i][j])%mod;}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){s1[i][j]=(s1[i-1][j]*bs2+s1[i][j])%mod;s2[i][j]=(s2[i-1][j]*bs2+s2[i][j])%mod;s3[i][j]=(s3[i-1][j]*bs2+s3[i][j])%mod;}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){int l=1,r=n,mid;while(l<=r){mid=l+r>>1;if(check(i-mid+1,j-mid+1,i+mid,j+mid)) l=mid+1;else r=mid-1;}ans+=l-1;}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){int l=1,r=n,mid;while(l<=r){mid=l+r>>1;if(check(i-mid,j-mid,i+mid,j+mid)) l=mid+1;else r=mid-1;}ans+=l-1;}}ans+=n*m;printf("%lld",ans);return 0;
}
相关文章:

ZJOI2009 对称的正方形
P2601 [ZJOI2009] 对称的正方形 题目大意 给定一个 n m n\times m nm的矩阵,求这个矩阵中满足上下对称且左右对称的正方形子矩阵的个数。 1 ≤ n , m ≤ 1000 1\leq n,m\leq 1000 1≤n,m≤1000 题解 首先,我们对原矩阵、左右翻转后的矩阵、上下翻转后…...
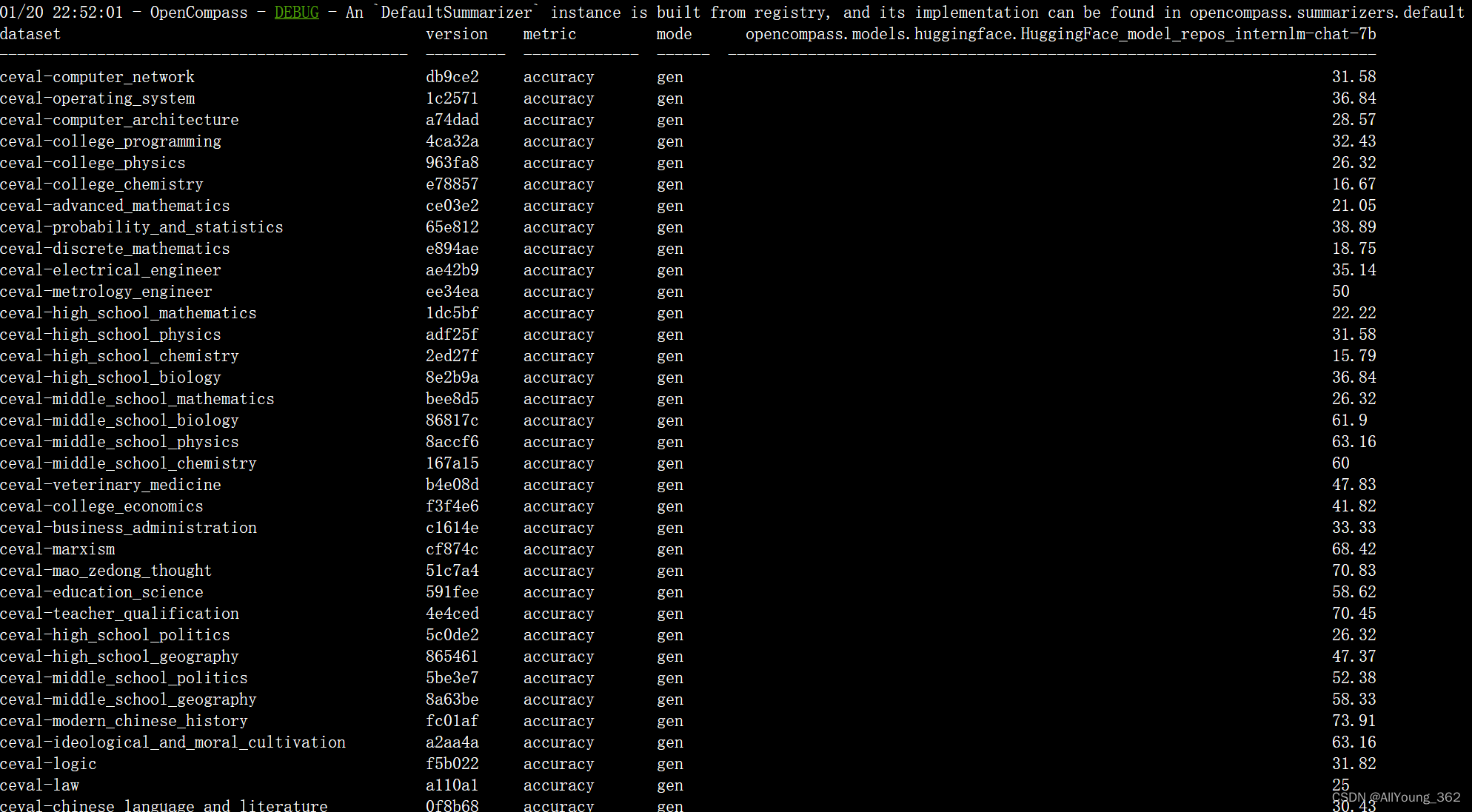
大模型学习与实践笔记(十一)
一、使用OpenCompass 对模型进行测评 1.环境安装: git clone https://github.com/open-compass/opencompass cd opencompass pip install -e . 当github超时无法访问时,可以在原命令基础上加上地址: https://mirror.ghproxy.com git clon…...
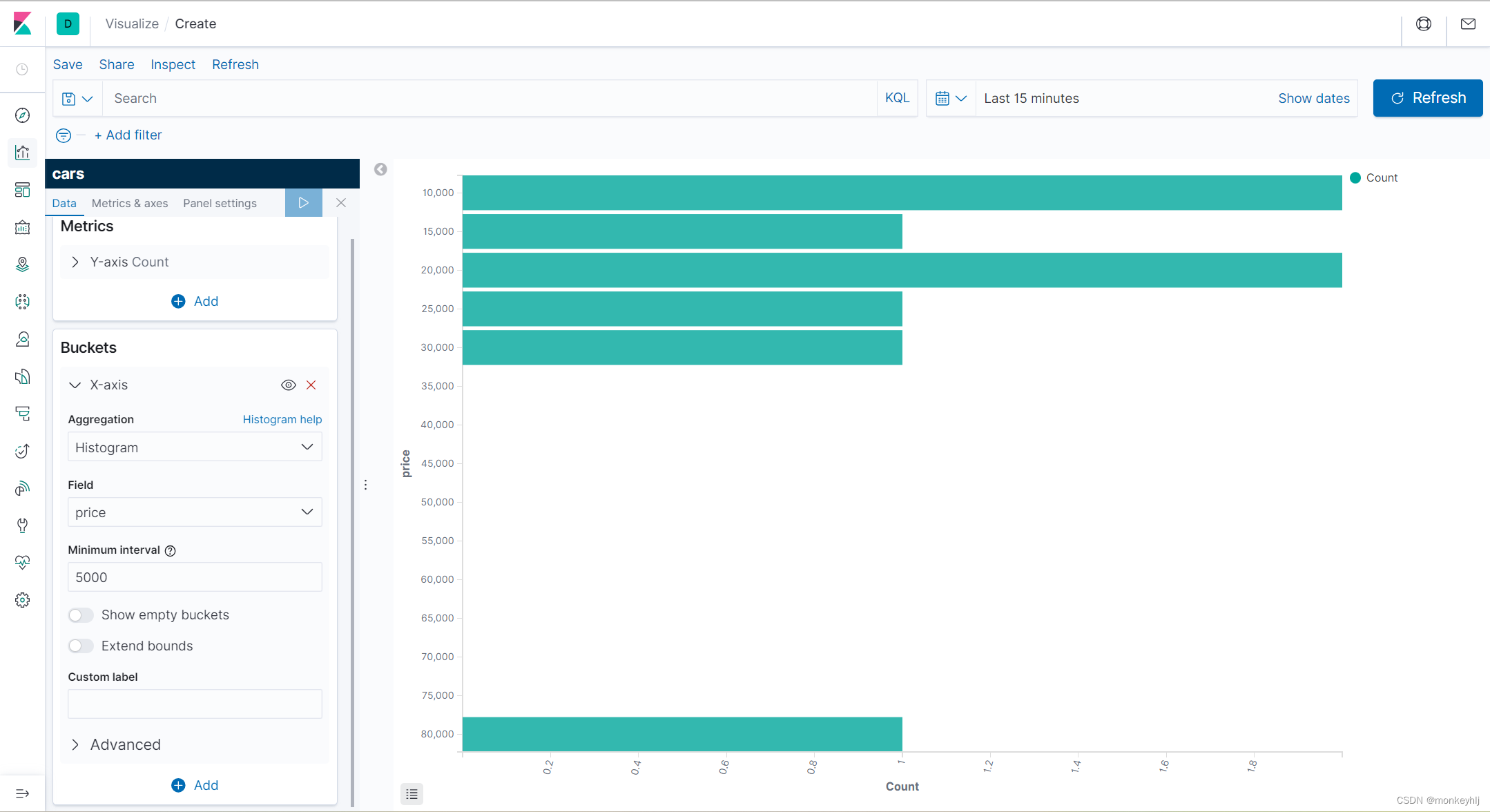
Elasticsearch+Kibana 学习记录
文章目录 安装Elasticsearch 安装Kibana 安装 Rest风格API操作索引基本概念示例创建索引查看索引删除索引映射配置(不配置好像也行、智能判断)新增数据随机生成ID自定义ID 修改数据删除数据 查询基本查询查询所有(match_all)匹配查…...

Cesium叠加超图二维服务、三维场景模型
前言 Cesium作为开源的库要加超图的服务则需要适配层去桥接超图与Cesium的数据格式。这个工作iClient系列已经做好,相比用过超图二维的道友们可以理解:要用Openlayer加载超图二维,那就用iClient for Openlayer库去加载;同样的要用…...

【低危】OpenSSL 拒绝服务漏洞
漏洞描述 OpenSSL 是广泛使用的开源加密库。 在 OpenSSL 3.0.0 到 3.0.12, 3.1.0 到 3.1.4 和 3.2.0 中 ,使用函数 EVP_PKEY_public_check() 来检查 RSA 公钥的应用程序可能会遇到长时间延迟。如果检查的密钥是从不可信任的来源获取的,这可能会导致拒绝…...

TDL-Tiny Synopsis-TED-ED 网络理论 Network Theory
Tiny Synopsis on TED-ED-Network Theory I) Webpage addressII)Context ExceptionIII) Diagram/Chart Research&Developement I) Webpage address URL Resource II)Context Exception what does “going viral” on Internet really mean? (网络…...

GIS项目实战08:JetBrains IntelliJ IDEA 2022 激活
为什么选择 IntelliJ IDEA 使用编码辅助功能更快地编写高质量代码,这些功能可在您键入时搜索可能的错误并提供改进建议,同时无缝地向您介绍编码、新语言功能等方面的社区最佳实践。 IntelliJ IDEA 了解您的代码,并利用这些知识通过在每种上…...
Linux 命令大全 CentOS常用运维命令
文章目录 1、Linux 目录结构2、解释目录3、命令详解3.1、shutdown命令3.1、文件目录管理命令ls 命令cd 命令pwd 命令tree 命令mkdir 命令touch 命令cat 命令cp 命令more 命令less 命令head 命令mv 命令rm 命令ln 命令tail 命令cut命令 3.2、用户管理useradd/userdel 命令用户的…...

6.3.5编辑视频
6.3.5编辑视频 除了上面的功能外,Camtasia4还能进行简单的视频编辑工作,如媒体的剪辑、连接、画中画等。 下面我们就利用Camtasia4的强大功能来实现一个画中画效果,在具体操作之前,需要准备好两个视频文件,一个作为主…...

同星多通道CAN FD转USB/WIFI设备,解决近距离无线通讯问题
新品发布/New products release 2024年1月,同星智能连续发布FlexRay系列产品TP1034和以太网系列产品TP1051,上周发布多通道总线记录仪产品TLog1004。1月19日,同星智能又推出一款2/4路CAN FD转USB和WIFI的工具,解决近距离无线通讯…...

wamp环境的组成
wamp环境介绍 简介 Wamp 就是 Windows Apache Mysql PHP集成安装环境,即在window下的apache、php和mysql的服务器软件。 w--windows Windows操作系统,是由美国微软公司(Microsoft)研发的操作系统,问世于1985年。起初…...
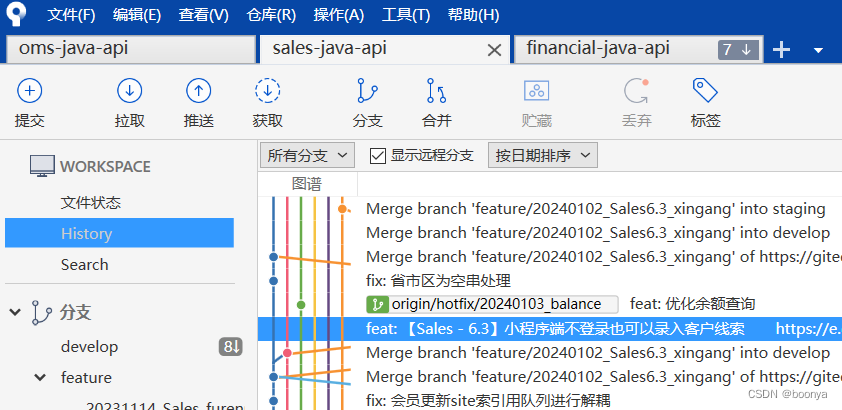
Idea 开发环境不断切换git代码分支导致冲掉别人代码
问题分析 使用git reflog查看执行命令,以下是发生事故的切换和提交动作 46f72622e1 HEAD{41}: commit: feat: 【Sales - 6.3】小程序端不登录也可以录入客户线索 c5e7d9f6e1 HEAD{42}: fetch origin feature/20240102_Sales6.3_xingang:feature/20240102_Sales6.3…...

GO 中如何防止 goroutine 泄露
文章目录 概述如何监控泄露一个简单的例子泄露情况分类chanel 引起的泄露发送不接收接收不发送nil channel真实的场景 传统同步机制MutexWaitGroup 总结参考资料 今天来简单谈谈,Go 如何防止 goroutine 泄露。 概述 Go 的并发模型与其他语言不同,虽说它…...

Linux练习题
1 简答题:请列举你所知道的Linux发行版 常见的Linux发行版: Red Hat Enterprise Linux 6/7/8 CentOS 6/7/8 Suse Linux Enterprise 15 Debian Linux 11 Ubuntu Linux 20.04/21.04 Rocky Linux 8/9 2 简答题:Linux系统的根目录、/dev目录的作用是什么 /:linux文件系统的…...
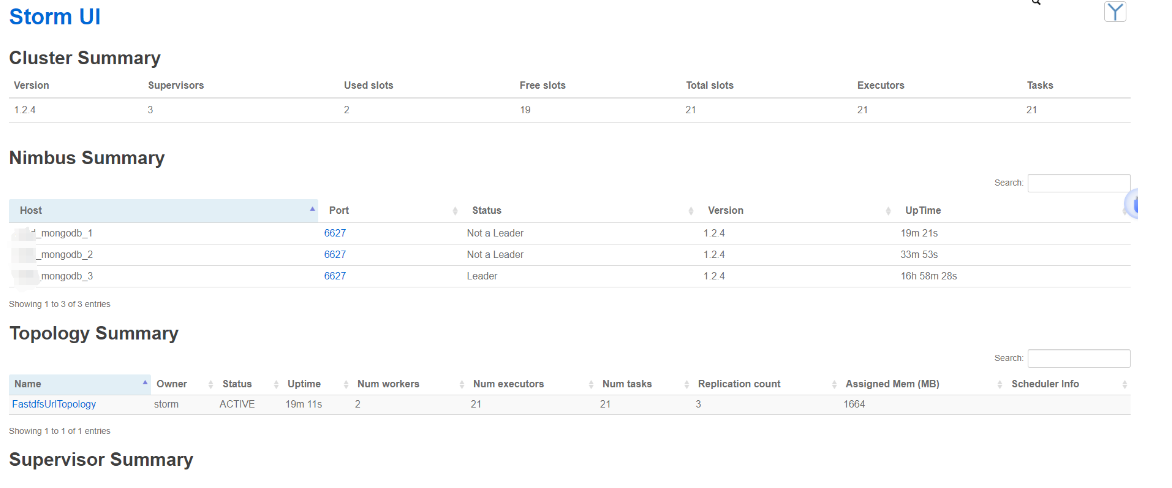
storm统计服务开启zookeeper、kafka 、Storm(sasl认证)
部署storm统计服务开启zookeeper、kafka 、Storm(sasl认证) 当前测试验证结果: 单独配置zookeeper 支持acl 设置用户和密码,在storm不修改代码情况下和kafka支持当kafka 开启ACL时,storm 和ccod模块不清楚配置用户和密…...

YOLOv8加入AIFI模块,附带项目源码链接
YOLOv8" 是一个新一代的对象检测框架,属于YOLO(You Only Look Once)系列的最新版本。YOLOv8中提及的AIFI(Attention-based Intrascale Feature Interaction)模块是一种用于增强对象检测性能的机制,它是…...
【设计模式】代理模式的实现方式与使用场景
1. 概述 代理模式是一种结构型设计模式,它通过创建一个代理对象来控制对另一个对象的访问,代理对象在客户端和目标对象之间充当了中介的角色,客户端不再直接访问目标对象,而是通过代理对象间接访问目标对象。 那在中间加一层代理…...

医学图像的图像处理、分割、分类和定位-1
一、说明 本报告全面探讨了应用于医学图像的图像处理和分类技术。开展了四项不同的任务来展示这些方法的多功能性和有效性。任务 1 涉及读取、写入和显示 PNG、JPG 和 DICOM 图像。任务 2 涉及基于定向变化的多类图像分类。此外,我们在任务 3 中包括了胸部 X 光图像…...
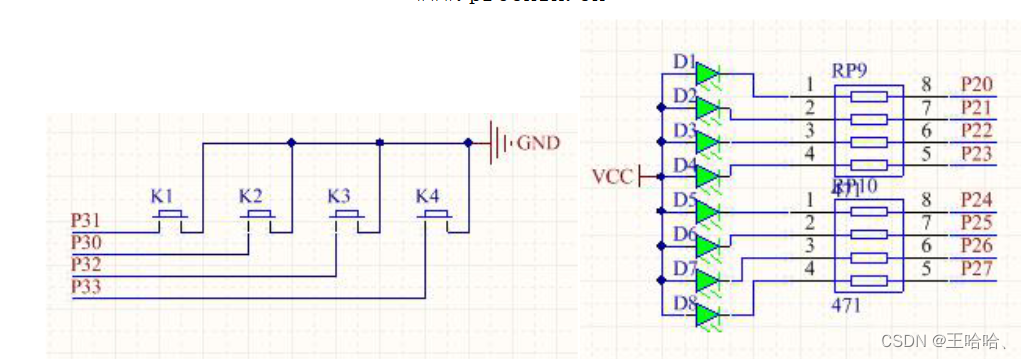
【51单片机】外部中断
0、前言 参考:普中 51 单片机开发攻略 第16章 及17章 1、硬件 2、软件 #include <reg52.h> #include <intrins.h> #include "delayms.h"typedef unsigned char u8; typedef unsigned int u16;sbit led P2^0; sbit key3 P3^2;//外部中断…...

fastapi框架
fastapi框架 fastapi,一个用于构建 API 的现代、快速(高性能)的异步web框架。 fastapi是建立在Starlette和Pydantic基础上的 Pydantic是一个基于Python类型提示来定义数据验证、序列化和文档的库。Starlette是一种轻量级的ASGI框架/工具包…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
