【动态规划】【广度优先搜索】【状态压缩】847 访问所有节点的最短路径
作者推荐
视频算法专题
本文涉及知识点
动态规划汇总
广度优先搜索 状态压缩
LeetCode847 访问所有节点的最短路径
存在一个由 n 个节点组成的无向连通图,图中的节点按从 0 到 n - 1 编号。
给你一个数组 graph 表示这个图。其中,graph[i] 是一个列表,由所有与节点 i 直接相连的节点组成。
返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止,也可以多次重访节点,并且可以重用边。
示例 1:
输入:graph = [[1,2,3],[0],[0],[0]]
输出:4
解释:一种可能的路径为 [1,0,2,0,3]
示例 2:
输入:graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
输出:4
解释:一种可能的路径为 [0,1,4,2,3]
参数范围:
n == graph.length
1 <= n <= 12
0 <= graph[i].length < n
graph[i] 不包含 i
如果 graph[a] 包含 b ,那么 graph[b] 也包含 a
输入的图总是连通图
广度优先搜索
需要记录那些节点已经访问,用状态压缩 (1 << i )表示第i个节点已访问。
还要记录此路径的最后节点。
这两个状态相同,后面的路径则相同。 由于是广度优先搜索,所以路径短的先处理,每个状态只会处理一次。
vDis 记录各状态的最短路径数。
que 记录状态。
时间复杂度:O(n2nn) 枚举起点O(n) 枚举状态数O(2^n) 每个状态处理。
核心代码
class Solution {
public:int shortestPathLength(vector<vector<int>>& graph) {m_c = graph.size();m_iMaskCount = 1 << m_c;for (int i = 0; i < m_c; i++){BFS(graph, i);}return m_iRet;}void BFS(vector<vector<int>>& neiBo,int start){vector<vector<int>> vDis(m_c, vector<int>(m_iMaskCount, m_iNotMay));queue<pair<int, int>> que;auto Add = [&](int node, int iPreMask,int iNew){const int iMask = iPreMask | (1 << node);if (vDis[node][iMask] <= iNew ){return ;}vDis[node][iMask] = iNew;que.emplace(node, iMask);};Add( start,0, 0);while (que.size()){auto [preNode, preMask] = que.front();const int iNew = vDis[preNode][preMask]+1;que.pop();for (const auto& next : neiBo[preNode]){Add(next, preMask, iNew);}}for (const auto& v : vDis){m_iRet = min(m_iRet, v.back());}}const int m_iNotMay = 100'000;int m_c, m_iMaskCount;int m_iRet = m_iNotMay;
};
测试用例
template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{ vector<vector<int>> graph;{Solution sln;graph = { {1,2,3},{0},{0},{0} };auto res = sln.shortestPathLength(graph);Assert(res, 4);}{Solution sln;graph = { {1},{0,2,4},{1,3,4},{2},{1,2} };auto res = sln.shortestPathLength(graph);Assert(res, 4);}}动态规划
节点的距离用多源路径的最短距离。
动态规划的状态表示
mask&(1 << next)表示经过了next节点。
vDis[node][mask] 有以下两种含义:
一, 以node结尾,经过mask指定节点的最短路径经过的节点数。
二,以node结尾,且只经过node节点一次,经过mask指定节点的最短路径经过的节点数。
含义二,如果存在,则是含义二,否则是含义一。 必须枚举所有符合含义二的可能。
动态规划的转移方程
vDis[next][maks|next]= MinSelf n e x t = 0 m c − 1 \Large_{next=0}^{m_c-1} next=0mc−1vDis[i][mask]+距离(i,next)
vDis[i][mask] 必须合法,且mask不包括next节点
动态规划的填表顺序
mask从1到大,确保动态规划的无后效性。某路径的编码是mask,经过新节点next后,新编码为iNewMask。则iNewMask-mask = 1 << next
1 << next 恒大于0。
动态规划的初始值
全部为不存在的数
动态规划的返回值
Min j = 0 m c − 1 \Large_{j=0}^{m_c-1} j=0mc−1vDis[j].back() -1
证明
将最短路径的重复节点删除,保留任意一个。删除后为: i 1 \Large_1 1 i 2 \Large_2 2 …i n \Large_n n 。任意i k \Large_k k到i k + 1 \Large_{k+1} k+1的路径一定是最短,否则替换成最短。直接枚举,12! 超时。 用动态规划,共2nn种状态,空间复杂度O(2nn),每种状态转移时间复杂度O(n),故总时间复杂度O(2nnn)。
代码
//多源码路径
template<class T, T INF = 1000 * 1000 * 1000>
class CFloyd
{
public:CFloyd(const vector<vector<T>>& mat){m_vMat = mat;const int n = mat.size();for (int i = 0; i < n; i++){//通过i中转for (int i1 = 0; i1 < n; i1++){for (int i2 = 0; i2 < n; i2++){//此时:m_vMat[i1][i2] 表示通过[0,i)中转的最短距离m_vMat[i1][i2] = min(m_vMat[i1][i2], m_vMat[i1][i] + m_vMat[i][i2]);//m_vMat[i1][i2] 表示通过[0,i]中转的最短距离}}}};vector<vector<T>> m_vMat;
};class Solution {
public:int shortestPathLength(vector<vector<int>>& graph) {m_c = graph.size();m_iMaskCount = 1 << m_c;vector<vector<int>> mat(m_c, vector<int>(m_c, 1000 * 1000 * 1000));for (int i = 0; i < m_c; i++){for (const auto& j : graph[i]){mat[i][j] = 1;}}CFloyd floyd(mat);vector<vector<int>> vDis(m_c, vector<int>(m_iMaskCount, m_iNotMay));for (int i = 0; i < m_c; i++){ vDis[i][1 << i] = 1;}for (int mask = 1; mask < m_iMaskCount; mask++){for (int i = 0; i < m_c; i++){if (vDis[i][mask] >= m_iNotMay){continue;}for (int next = 0 ;next < m_c ;next++ ){if ((1 << next) & mask){continue;//已经访问}const int iNewMask = (1 << next) | mask;vDis[next][iNewMask] = min(vDis[next][iNewMask], vDis[i][mask] + floyd.m_vMat[i][next]);}}}int iRet = m_iNotMay;for (const auto& v : vDis){iRet = min(iRet, v.back());}return iRet-1;}const int m_iNotMay = 100'000;int m_c, m_iMaskCount;};
2023年1月
class Solution {
public:
int shortestPathLength(vector<vector>& graph) {
auto Add = [this](int iMask, int iPos, int iOpeNum)
{
if (INT_MAX != m_vMaskPosMinOpe[iMask][iPos])
{
return;
}
m_vQue.emplace_back(iMask, iPos);
m_vMaskPosMinOpe[iMask][iPos] = iOpeNum;
};
m_c = graph.size();
for (int i = 0; i < sizeof(m_vMaskPosMinOpe) / sizeof(m_vMaskPosMinOpe[0]); i++)
{
for (int j = 0; j < sizeof(m_vMaskPosMinOpe[0]) / sizeof(m_vMaskPosMinOpe[0][0]); j++)
{
m_vMaskPosMinOpe[i][j] = INT_MAX;
}
}
for (int i = 0; i < m_c; i++)
{
Add(1 << i, i, 0);
}
for (int i = 0; i < m_vQue.size(); i++)
{
const int iMask = m_vQue[i].first;
const int iPos = m_vQue[i].second;
for (auto& next : graph[iPos])
{
int iNewMask = iMask | (1 << next);
Add(iNewMask, next, m_vMaskPosMinOpe[iMask][iPos] + 1);
}
}
int iMin = INT_MAX;
for (int i = 0; i < sizeof(m_vMaskPosMinOpe[0]) / sizeof(m_vMaskPosMinOpe[0][0]); i++)
{
iMin = min(iMin, m_vMaskPosMinOpe[(1 << m_c) - 1][i]);
}
return iMin;
}
vector<std::pair<int,int>> m_vQue;
int m_vMaskPosMinOpe[1 << 12 ][12];
int m_c;
};
2023年8月
class Solution {
public:
int shortestPathLength(vector<vector>& graph) {
auto Add = [this](int iMask, int iPos, int iOpeNum)
{
if (INT_MAX != m_vMaskPosMinOpe[iMask][iPos])
{
return;
}
m_vQue.emplace_back(iMask, iPos);
m_vMaskPosMinOpe[iMask][iPos] = iOpeNum;
};
m_c = graph.size();
for (int i = 0; i < sizeof(m_vMaskPosMinOpe) / sizeof(m_vMaskPosMinOpe[0]); i++)
{
for (int j = 0; j < sizeof(m_vMaskPosMinOpe[0]) / sizeof(m_vMaskPosMinOpe[0][0]); j++)
{
m_vMaskPosMinOpe[i][j] = INT_MAX;
}
}
for (int i = 0; i < m_c; i++)
{
Add(1 << i, i, 0);
}
for (int i = 0; i < m_vQue.size(); i++)
{
const int iMask = m_vQue[i].first;
const int iPos = m_vQue[i].second;
for (auto& next : graph[iPos])
{
int iNewMask = iMask | (1 << next);
Add(iNewMask, next, m_vMaskPosMinOpe[iMask][iPos] + 1);
}
}
int iMin = INT_MAX;
for (int i = 0; i < sizeof(m_vMaskPosMinOpe[0]) / sizeof(m_vMaskPosMinOpe[0][0]); i++)
{
iMin = min(iMin, m_vMaskPosMinOpe[(1 << m_c) - 1][i]);
}
return iMin;
}
vector<std::pair<int,int>> m_vQue;
int m_vMaskPosMinOpe[1 << 12 ][12];
int m_c;
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【广度优先搜索】【状态压缩】847 访问所有节点的最短路径
作者推荐 视频算法专题 本文涉及知识点 动态规划汇总 广度优先搜索 状态压缩 LeetCode847 访问所有节点的最短路径 存在一个由 n 个节点组成的无向连通图,图中的节点按从 0 到 n - 1 编号。 给你一个数组 graph 表示这个图。其中,graph[i] 是一个列…...

python基础小知识:引用和赋值的区别
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 1.引用 python中,赋值操作会产生相同对象的多个引用, 如果在原位置修改这个可变对象时,可能会影响程序其他位置对这个对象的…...
欧科云链与《警察技术》联合发布技术专题.pdf
欧科云链受《警察技术》邀请,于第201期期刊正式刊登“区块链生态安全与虚拟货币犯罪治理”技术专题。欧科云链作为该技术专题主要作者,直接参与本次期刊2篇文章撰写,同时为多篇文章提供欧科云链的最新数据和研究成果。 《警察技术》期刊创办于…...
【QT+QGIS跨平台编译】之一:【sqlite+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、sqlite3介绍二、文件下载三、文件分析四、pro文件五、编译实践 一、sqlite3介绍 SQLite是一款轻型的数据库,是遵守ACID的关系型数据库管理系统,它包含在一个相对小的C库中。它是D.RichardHipp建立的公有领域项目。它的设计目标是嵌入式的&…...
websocket实现聊天室(vue2 + node)
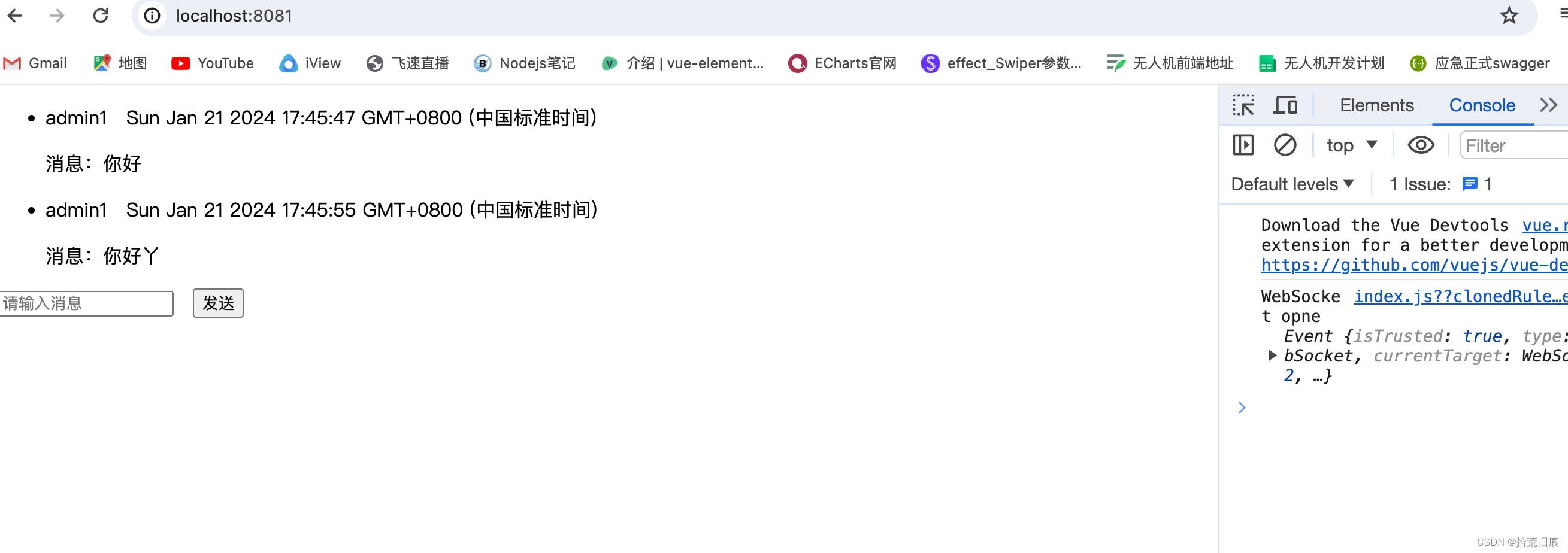
通过websocket实现简单的聊天室功能 需求分析如图: 搭建的项目结构如图: 前端步骤: vue create socket_demo (创建项目)views下面建立Home , Login组件路由里面配置路径Home组件内部开启websocket连接 前端相关组件代码: Login…...
RabbitMQ-消息延迟
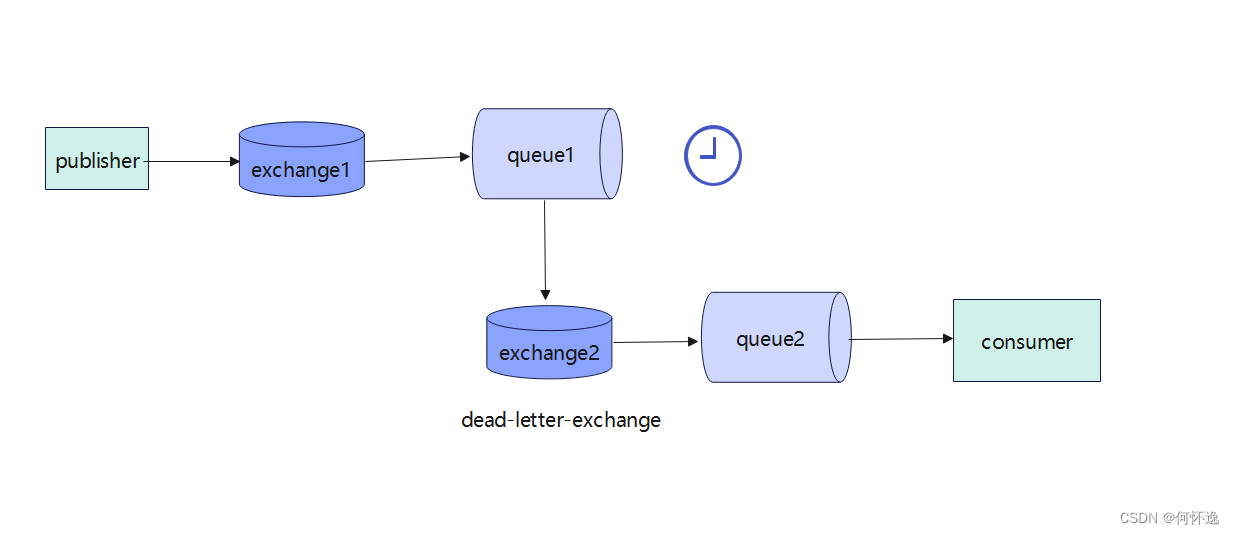
一、死信交换机 1、描述 一个队列接收到的消息有过期时间,消息过期之后,如果配置有死信队列,消息就会进去死信队列。 2、图解 3、过程 当生产者将消息发送到exchange1,然后交换机将消息路由到队列queue1,但是队列que…...

【Oracle】如何给物化视图分区
文章目录 【Oracle】如何给物化视图分区给物化视图进行分区的例 【声明】文章仅供学习交流,观点代表个人,与任何公司无关。 编辑|SQL和数据库技术(ID:SQLplusDB) 收集Oracle数据库内存相关的信息 【Oracle】ORA-32017和ORA-00384错误处理 【Oracle】设置…...

10个常考的前端手写题,你全都会吗?
前言 📫 大家好,我是南木元元,热爱技术和分享,欢迎大家交流,一起学习进步! 🍅 个人主页:南木元元 今天来分享一下10个常见的JavaScript手写功能。 目录 1.实现new 2.call、apply、…...

vue组件间通信
Vue组件之间通信方式有哪些 一、父子组件通讯 1、props,emit 父组件可以通过props给子组件传递变量。子组件可以通过emit派发自定义事件,使父组件可以获得事件函数传递过来的形参。 2、$parent、$children、ref 父组件可以通过 c h i l d r e n 获取…...

编程框架概述:MVC, MVP, MVVM, Flux/Redux, 和 Clean Architecture
前言 在软件开发中,选择合适的编程框架和架构模式对于构建可维护和可扩展的应用程序至关重要。初学者在面对多种架构选项时可能会感到困惑。本文将详细介绍五种流行的编程框架:MVC、MVP、MVVM、Flux/Redux和Clean Architecture。 MVC(Model-V…...

多维时序 | Matlab实现CNN-BiLSTM-Mutilhead-Attention卷积双向长短期记忆神经网络融合多头注意力机制多变量时间序列预测
多维时序 | Matlab实现CNN-BiLSTM-Mutilhead-Attention卷积双向长短期记忆神经网络融合多头注意力机制多变量时间序列预测 目录 多维时序 | Matlab实现CNN-BiLSTM-Mutilhead-Attention卷积双向长短期记忆神经网络融合多头注意力机制多变量时间序列预测效果一览基本介绍程序设计…...

np.argsort排序问题(关于位次)-含GitHub上在numpy项目下提问的回复-总结可行方案
np.argsort 与获取位相关问题 位次: 数组中的数据在其排序之后的另一个数组中的位置 [1,0,2,3] 中 0的位次是1 1的位次是2 2的位次是3 3的位次是4 这里先直接给出结论,np.argsort()返回的索引排序与实际位次在确实在某些情况下会出现一致,但后来numpy的开…...

Element中的el-input-number+SpringBoot+mysql
1、编写模板 <el-form ref"form" label-width"100px"><el-form-item label"商品id:"><el-input v-model"id" disabled></el-input></el-form-item><el-form-item label"商品名称&a…...

Jupyter Notebook五分钟基础速通
1 作用 常用于数据分析 2 安装 2.1 Anaconda 通过直接安装Anaconda,会自动安装Jupyter Notebook 2.2 命令行安装 ① 3.x版本 pip3 install --upgrade pip pip3 install jupyter ② 2.x版本 pip install --upgrade pip pip install jupyter 3 启动 cmd窗口下…...
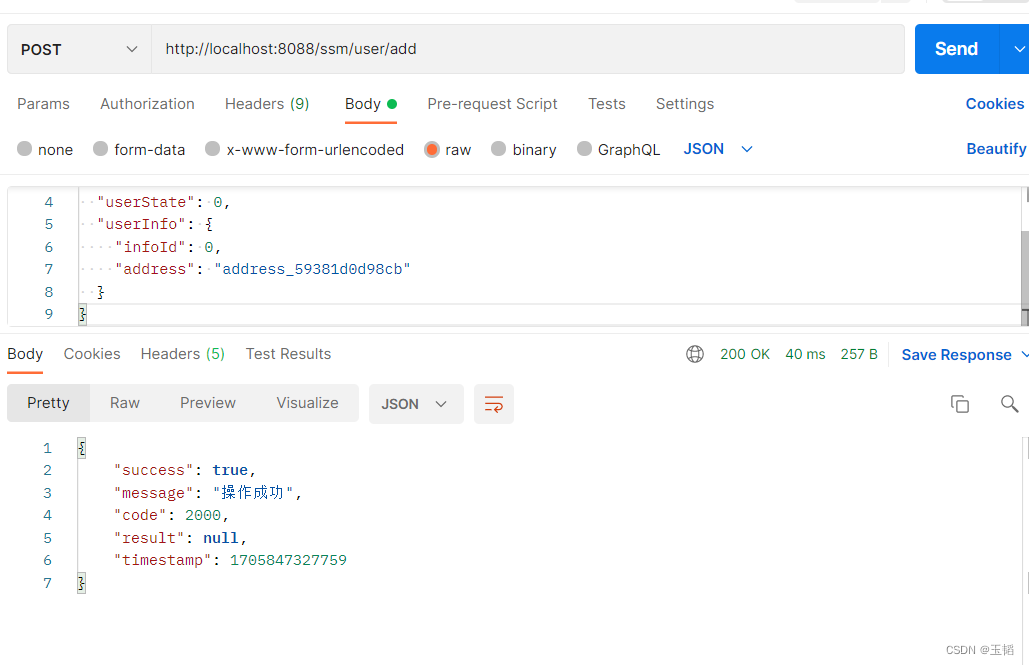
基于SpringBoot的SSM整合案例
项目目录: 数据库表以及表结构 user表结构 user_info表结构 引入依赖 父模块依赖: <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.2.12.RELEASE</version>…...
[SS]语义分割_转置卷积
转置卷积(Transposed Convolution) 抽丝剥茧,带你理解转置卷积(反卷积) 目录 一、概念 1、定义 2、运算步骤 二、常见参数 一、概念 1、定义 转置卷积(Transposed Convolution)…...

面板小程序命令行工具介绍
Ray 体系提供配套的工程化解决方案。 由于多端构建的一些客观原因,在构建流程的设计上,必须将工程套件安装在项目内。 项目内的依赖至少包含以下内容: {"dependencies": {"ray-js/ray": "latest"},"de…...

DBA技术栈MongoDB: 数据增改删除
该博文主要介绍mongoDB对文档数据的增加、更新、删除操作。 1.插入数据 以下案例演示了插入单个文档、多个文档、指定_id、指定多个索引以及插入大量文档的情况。在实际使用中,根据需求选择适合的插入方式。 案例1:插入单个文档 db.visitor.insert({…...
Xcode查看APP文件目录
一、连接真机到MAC电脑上 二、打开Devices 点击window -> Devices and Simulatores 三、选中设备、选择app 四、选择下载内容 五、查看文件内容 得到的文件 右键显示包内容,获得APP内数据 六、分发证书无法下载 使用分发的证书无法下载文件内容…...
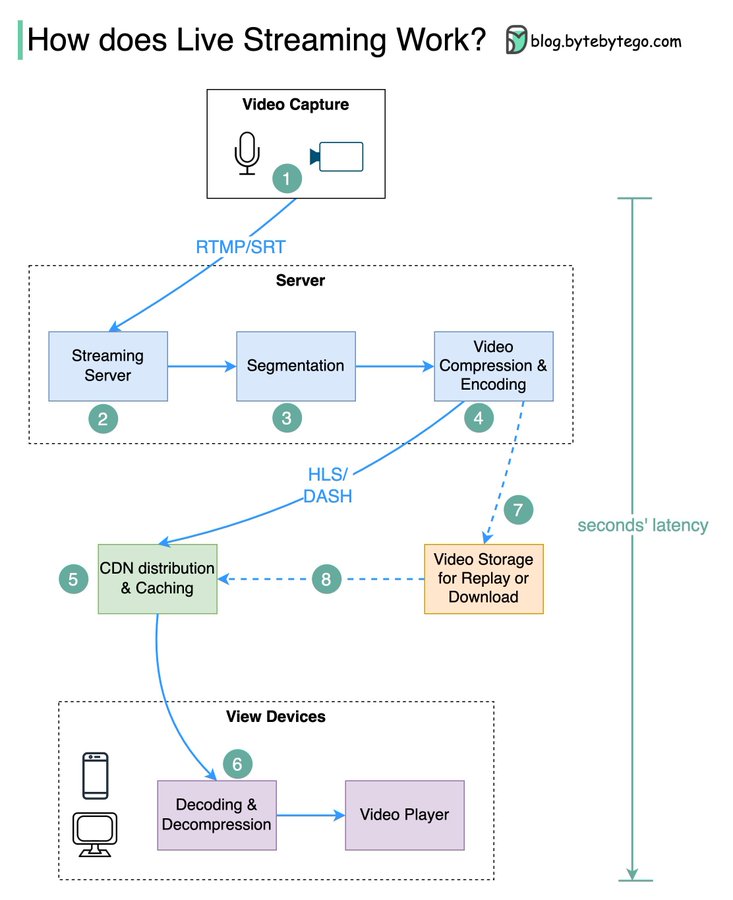
【视频媒体】深入了解直播视频流
深入了解直播视频流🎥 YouTube、TikTok live和Twitch上的直播视频是如何工作的? 直播视频流与常规流媒体不同,因为视频内容通过互联网近乎实时发送,通常只有几秒钟的延迟。 下图解释了实现这一目标背后所发生的事情。 步骤1&…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
