枚举算法(穷举法)(暴力法)
1.什么是枚举
枚举是指在一定范围内将所有情况一一列举,再通过条件判断得到自己想要的答案;
2.枚举核心

3.使用枚举的基本步骤

4.例题
4.1.我国古代数学家张丘建在他的《算经》一书中提出了著名的“百钱买百鸡”问题:鸡翁一值钱五;鸡母一值钱三;鸡雏三值钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?
枚举对象:坤翁:x;坤母:y;坤雏:z(100 - x - y);
枚举范围(最大值为100钱全买同一种的数量):坤翁0~20;坤母0~33;坤雏0~100(个数上限为100)
判断条件:共一百只且共一百钱
#include<iostream>int main()
{using namespace std;for (int x = 0; x <= 20; x++){for (int y = 0; y <= 33; y++){for (int z = 0; z <= 100; z++){if ((x + y + z == 100) && (x * 5 + y * 3 + z / 3 == 100))cout << x << ' ' << y << ' ' << z << endl;}}}return 0;
}但是三层循环效率太低,可以优化成:
#include<iostream>int main()
{using namespace std;for (int x = 0; x <= 20; x++){for (int y = 0; y <= 33; y++){if ((x * 5 + y * 3 + (100 - x - y) / 3 == 100))cout << x << ' ' << y << ' ' << (100 - x - y) << endl;}}return 0;
}4.2对于长度为5位的一个o1串,每一位都可能是О或1,一共有32种可能。
它们的前几个是:
00000
00001
00010
00011
00100
00101
00110
00111
请按从小到大的顺序输出这32种01串。
#include<iostream>int main()
{using namespace std;int count = 0;for (int a = 0; a <= 1; a++){for (int b = 0; b <= 1; b++){for (int c = 0; c <= 1; c++){for (int d = 0; d <= 1; d++){for (int e = 0; e <= 1; e++){++count;cout << a << b << c << d << e << endl;}}}}}cout << count << endl;return 0;
}4.3将一个数进行质因数分解并输出
短除法:

#include <iostream>int main()
{using namespace std;int n;cin >> n;for (int i = 2; i <= n; i++){while (n % i == 0){cout << i << ' ';n = n / i;}}return 0;
}
由于2是最小的质数,同时2是检验偶数的标准,所以一直除以2直到不能整除时,n就为奇数,
然后就换下一个能够整除的质数继续除,直到n = 1;
4.4有一个n×m方格的棋盘,求其方格包含多少正方形、长方形(不包含正方形)。
输入格式:
一行,两个正整数n,m
输出格式
—行,两个正整数,分别表示方格包含多少正方形、长方形(不包含正方形)。

组合问题:
#include <iostream>int main()
{using namespace std;int n, m;int sum_Cube = 0;int sum_Cuboid = 0;cin >> n >> m;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (i == j)sum_Cube += (n - i + 1) * (m - j + 1);else{sum_Cuboid += (n - i + 1) * (m - j + 1);}}}cout << sum_Cube << ' ' << sum_Cuboid << endl;return 0;
}相关文章:

枚举算法(穷举法)(暴力法)
1.什么是枚举 枚举是指在一定范围内将所有情况一一列举,再通过条件判断得到自己想要的答案; 2.枚举核心 3.使用枚举的基本步骤 4.例题 4.1.我国古代数学家张丘建在他的《算经》一书中提出了著名的“百钱买百鸡”问题:鸡翁一值钱五;鸡母一值钱三;鸡雏三…...

计算机网络学习The next day
在计算机网络first day中,我们了解了计算机网络这个科目要学习什么,因特网的概述,三种信息交换方式等,在今天,我们就来一起学习一下计算机网络的定义和分类,以及计算机网络中常见的几个性能指标。 废话不多…...

ffmpeg中AVFrame解码linesize确定
一 测试环境 机型:Intel(R) Xeon(R) Gold 5218 ffmpeg版本4.3-dev 解码视频分辨率 720x1280 , 解码后 AVFrame linesize 768 解码视频分辨率 480x640, 解码后AVFrame linesize 512 二 linesize计算过程 avcodec_default_get_buffer2 -->update_frame_pool() --&g…...

数据可视化 | 期末复习 | 补档
文章目录 📚介绍可视化🐇什么是可视化🐇科学可视化,信息可视化,可视分析系统三者之间有什么区别🔥🐇可视化的基本流程🐇可视化的两个基本设计原则🐇数据属性🐇…...
【Docker】使用Docker安装Nginx及部署前后端分离项目应用
一、Nginx介绍 Nginx是一个高性能的HTTP和反向代理web服务器,同时也提供了IMAP/POP3/SMTP服务。它是由伊戈尔赛索耶夫为俄罗斯访问量第二的Rambler.ru站点开发的,公开版本1.19.6发布于2020年12月15日。其将源代码以类BSD许可证的形式发布,因它…...

28、web攻防——通用漏洞SQL注入HTTP头XFFCOOKIEPOST请求
文章目录 $_GET:接收get请求,传输少量数据,URL是有长度限制的; $_POST:接收post请求; $_COOKIE:接收cookie,用于身份验证; $_REQUEST:收集通过 GET 、POST和C…...

c++:类和对象(1),封装
C面向对象的三大特性:封装、继承、多态。 封装 封装的意义一: 将属性和行为作为一个整体,表现生活中的事物将属性和行为加以权限控制 类中的属性和行为,我们统一称为成员 属性也叫: 成员属性 成员变量 行为也叫&a…...
)
三、安全工程—安全架构(CISSP)
目录 一、安全工程 1.企业安全架构与系统安全架构 2.通用企业架构框架 2.1 Zachman框架...
《数组》)
Linux:shell脚本:基础使用(9)《数组》
数组就是一组数据类型相同集合 定义 数组名(元素内容…………) 如果没有元素内容就是空 arr1() # 定义了一个空数组 arr2(1 2 3 4 5 6 ) # 定义了一个元素是整形的数组 arr3("hello" "world" "你好" "世界") # 定义了一个元素为字符…...

TCP高并发服务器简介(select、poll、epoll实现与区别)
select、poll、epoll三者的实现: select实现TCP高并发服务器的流程: 一、创建套接字(socket函数):二、填充服务器的网络信息结构体:三、套接字和服务器的网络信息结构体进行绑定(bind函数&…...

Linux中的软件包管理器yum
目录 1.什么是软件包 2.关于 rzsz 3.查看软件包 4.如何安装软件 5.如何卸载软件 1.什么是软件包 ● 在Linux下安装软件, 一个通常的办法是下载到程序的源代码, 并进行编译, 得到可执行程序. ● 但是这样太麻烦了, 于是有些人把一些常用的软件提前编译好, 做成软件包(可以理…...
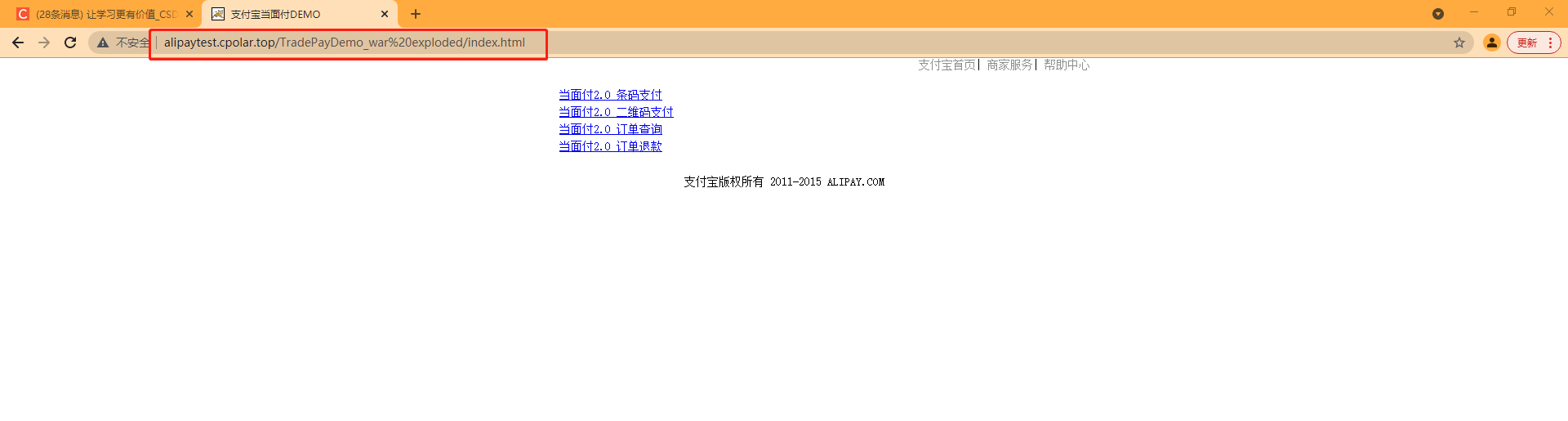
如何使用支付宝沙箱环境本地配置模拟支付并结合内网穿透远程调试
文章目录 前言1. 下载当面付demo2. 修改配置文件3. 打包成web服务4. 局域网测试5. 内网穿透6. 测试公网访问7. 配置二级子域名8. 测试使用固定二级子域名访问 正文开始前给大家推荐个网站,前些天发现了一个巨牛的 人工智能学习网站, 通俗易懂ÿ…...

解决子元素的click事件会触发父元素的dbclick事件
解决子元素的click事件会触发父元素的dbclick事件 方案一:方案二:方案三:方案一方案二综合案例如下: 方案一: 错误思路:通过阻止子元素click事件的冒泡,阻止父元素的dbclick 正确思路ÿ…...
)
算法训练营Day38(动态规划1)
动态规划理论基础 动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。 区别 动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心&…...
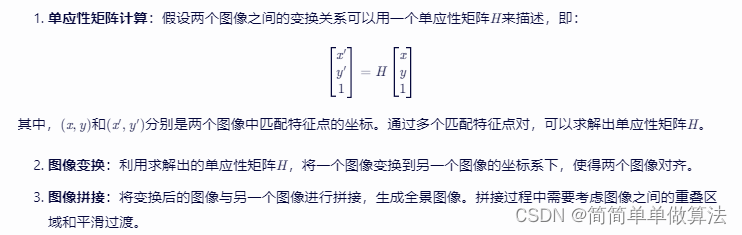
基于Harris角点的多视角图像全景拼接算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1 Harris角点检测 4.2 图像配准 4.3 图像变换和拼接 4.4 全景图像优化 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 function [ImageB…...

数学建模--PageRank算法的Python实现
文章目录 1. P a g e R a n k PageRank PageRank算法背景2. P a g e R a n k PageRank PageRank算法基础2.1. P a g e R a n k PageRank PageRank问题描述2.2.有向图模型2.3.随机游走模型 3. P a g e R a n k PageRank PageRank算法定义3.1. P a g e R a n k PageRank PageRank…...

samba服务搭建,并将共享目录映射到windows
系统版本:centos7 1、centos 安装samba yum -y install samba 2、查看安装信息 rpm -qa |grep samba 3、设置开机自启动 systemctl enable smb.service systemctl enable nmb.service 4、设置samba服务器配置文件 sudo vi /etc/samba/smb.conf 注意&#…...
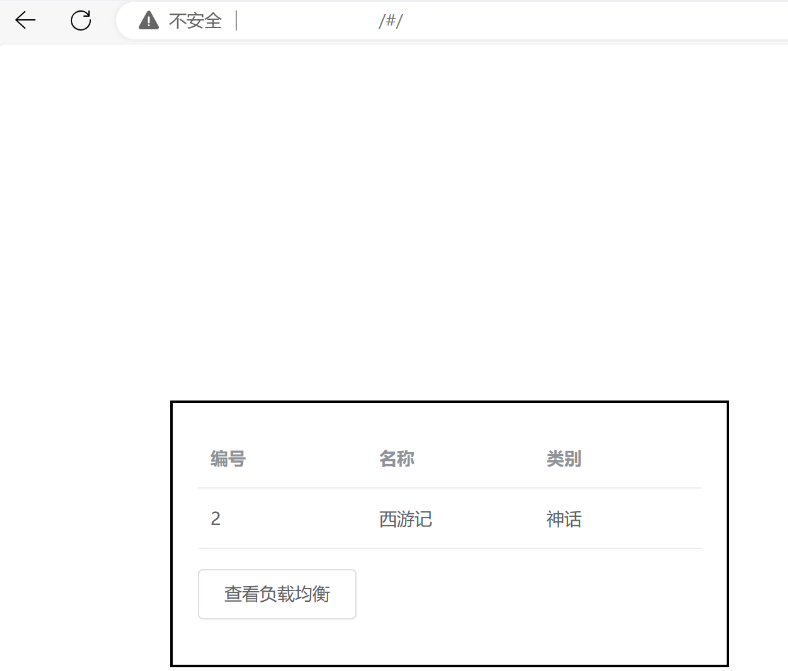
golang 中使用 statik 将静态资源编译进二进制文件中
现在的很多程序都会提供一个 Dashboard 类似的页面用于查看程序状态并进行一些管理的功能,通常都不会很复杂,但是其中用到的图片和网页的一些静态资源,如果需要用户额外存放在一个目录,也不是很方便,如果能打包进程序发…...

北京住总集团携手云轴科技ZStack获行业云平台领航者创新实践奖
为进一步促进行业企业上云、用数、赋智发展,落实国家政策,加速云计算应用从互联网拓展至政务、金融、交通、电信等行业,推动以云计算为核心的数字产业创新,1月18日中国信息通信研究院主办的“企业上云用云专项行动会—行业云平台研…...
【漏洞攻击之文件上传条件竞争】
漏洞攻击之文件上传条件竞争 wzsc_文件上传漏洞现象与分析思路编写攻击脚本和重放措施中国蚁剑拿flag wzsc_文件上传 漏洞现象与分析 只有一个upload前端标签元素,并且上传任意文件都会跳转到upload.php页面,判定是一个apache容器,开始扫描…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

【R语言编程——数据调用】
这里写自定义目录标题 可用库及数据集外部数据导入方法查看数据集信息 在R语言中,有多个库支持调用内置数据集或外部数据,包括studentdata等教学或示例数据集。以下是常见的库和方法: 可用库及数据集 openintro库 该库包含多个教学数据集&a…...
