电力系统系统潮流分析【IEEE 57 节点】(Matlab代码实现)
👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
潮流分析是研究电力系统的一种最基本和最重要的计算。最初,电力系统潮流计算是通过人工手算的,后来为了适应电力系统日益发展的需要,采用了交流计算台。随着电子数字计算机的出现,1956 年 Ward等人编制了实际可行的计算机潮流计算程序。这样,就为日趋复杂的大规模电力系统提供了极其有力的计算手段。经过几十年的时间,电力系统潮流计算已经发展得十分成熟。潮流计算是研究电力系统稳态运行情况的一种计算,是根据给定的运行条件及系统接线情况确定整个电
力系统各个部分的运行状态,如各母线的电压、各元件中流过的功率、系统的功率损耗等等。电力系统潮流计算是计算系统动态稳定和静态稳定的基础。在电力系统规划设计和现有电力系统运行方式的研究中,都需要利用电力系统潮流计算来定量的比较供电方案或运行方式的合理性、可靠性和经济性。
电力系统潮流计算是研究电力系统稳态运行情况的一种计算,它的任务是根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态,如各母线的电压(幅值及相角),各元件中流过的功率分布,系统的功率损耗等等。潮流计算是研究电力系统的一种最基本和最重要的计算。潮流计算的一般流程图如下:
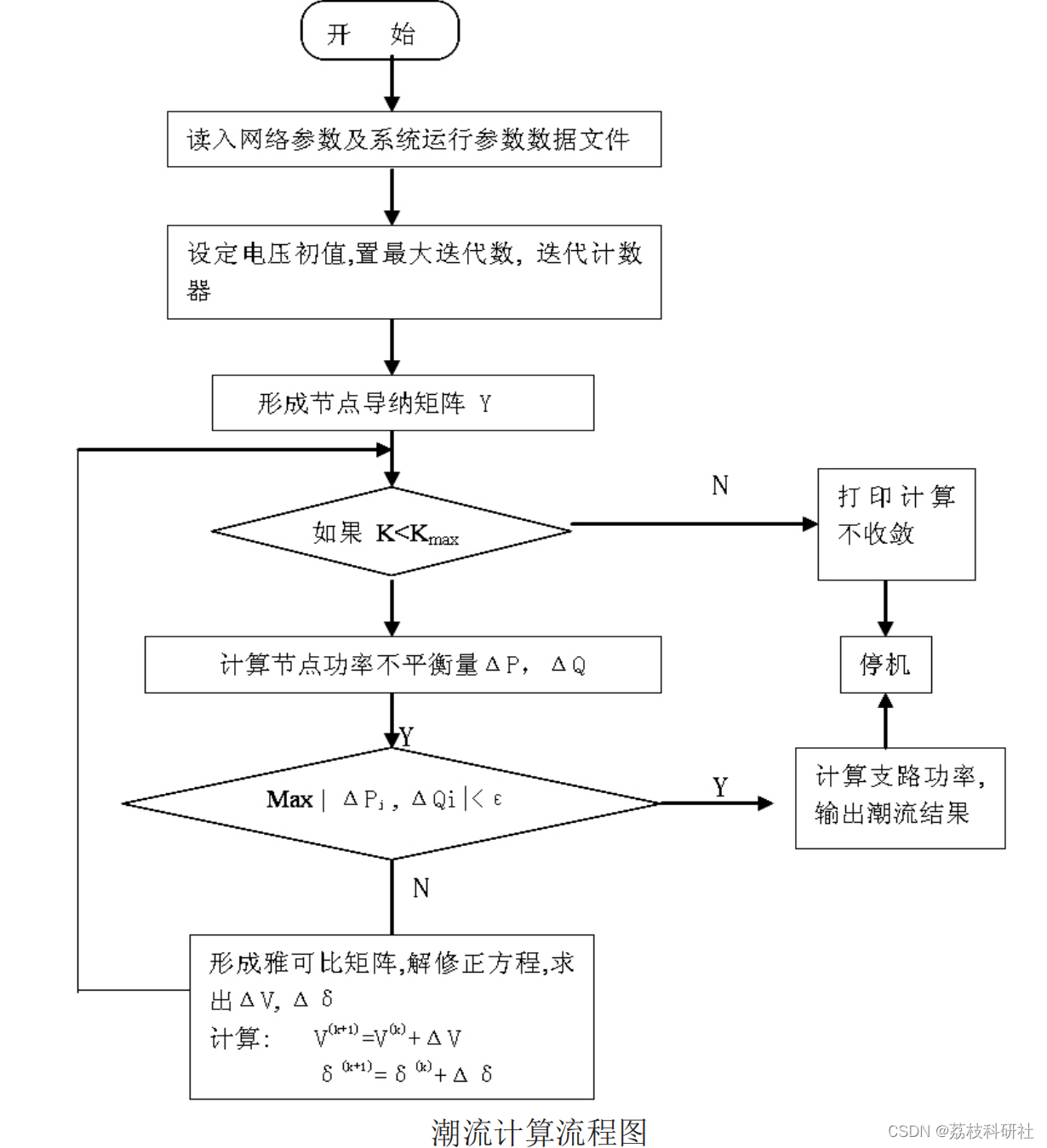

电力系统潮流计算的任务是在给定的电力系统运行条件下,计算电力系统的运行状态。电力系统运行条件是指电力系统各母线的负荷功率,发电机的功率,某些母线保持的电压值等。运行状态是指电力系统各母线的电压幅值和相角。电力系统运行状态一经确定,便可以计算出电力网络中功率分布和网损。
📚2 运行结果
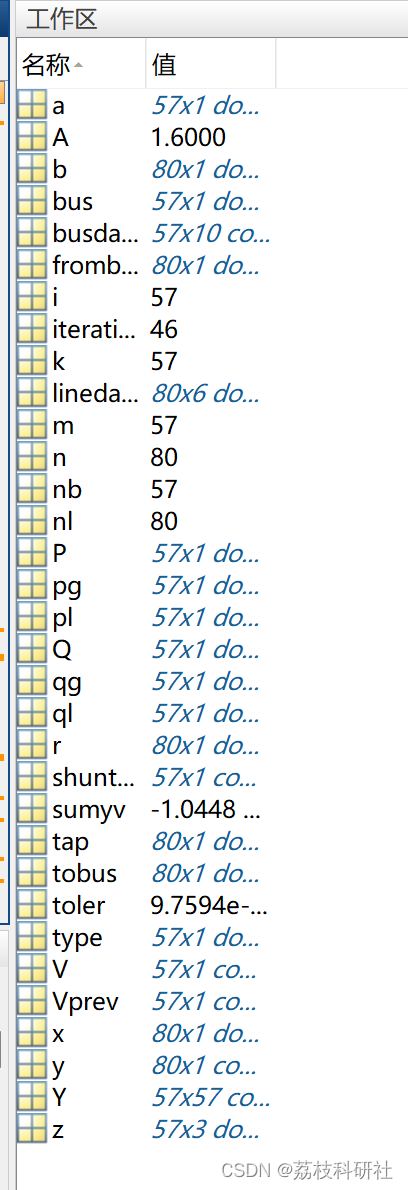

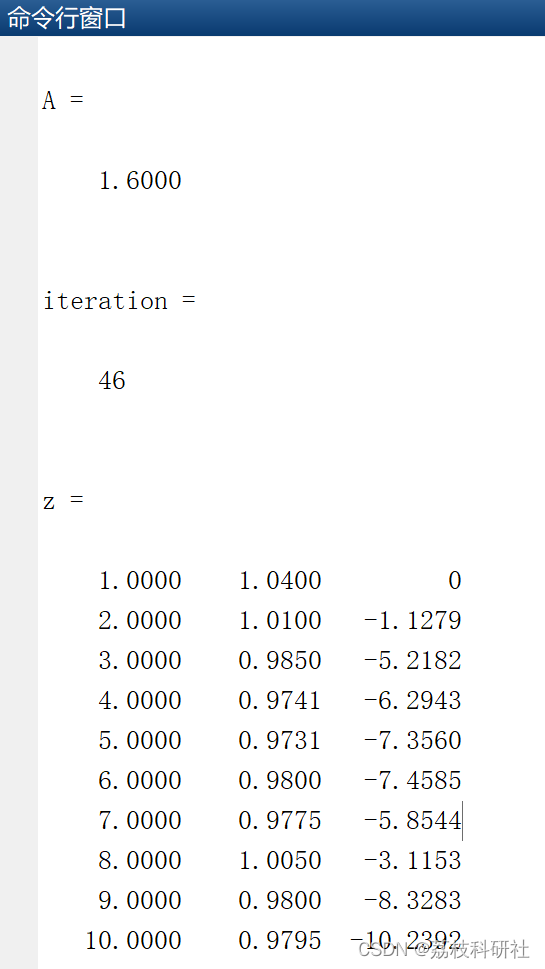

% IEEE 57 bus system
% % BUS NO V PHASE Pg Qg Pl Ql Qmax Qmin type
busdata=[ 1 1.040 0 0 0 0 0 0 0 1 ;
2 1.010 0 0 -0.8 3.0 88.0 50 -17 2 ;
3 .985 0 40 -1 41 21 60 -10 2 ;
4 1.000 0 0 0 0 0 0 0 3;
5 1.000 0 0 0 13 4 0 0 3;
6 .980 0 0 0.8 75 2 25 -8 2;
7 1.000 0 0 0 0 0 0 0 3;
8 1.005 0 450 62.1 150.0 22.0 200 -140 2;
9 0.980 0 0 2.2 121.0 26.0 9 -3 2;
10 1.000 0 0 0 5.0 2 0 0 3;
11 1.000 0 0 0 0 0 0 0 3;
12 1.015 0 310 128.5 377 24 155 -50 2;
13 1.000 0 0 0 18 2.3 0 0 3;
14 1.000 0 0 0 10.5 5.3 0 0 3;
15 1.000 0 0 0 22 5 0 0 3;
16 1.000 0 0 0 43 3 0 0 3;
17 1.000 0 0 0 42 8 0 0 3;
18 1.000 0 0 0 27.2 9.8 0 0 3;
19 1.000 0 0 0 3.3 0.6 0 0 3;
20 1.000 0 0 0 2.3 1.0 0 0 3;
21 1.000 0 0 0 0 0 0 0 3;
22 1.000 0 0 0 0 0 0 0 3;
23 1.008 0 0 0 6.3 2.1 0 0 3;
24 1.000 0 0 0 0 0 0 0 3;
25 1.000 0 0 0 6.3 3.2 0 0 3;
26 1.000 0 0 0 0 0 0 0 3;
27 1.000 0 0 0 9.3 0.5 0 0 3;
28 1.000 0 0 0 4.6 2.3 0 0 3;
29 1.000 0 0 0 17 2.6 0 0 3;
30 1.000 0 0 0 3.6 1.8 0 0 3;
31 1.000 0 0 0 5.8 2.8 0 0 3;
32 1.000 0 0 0 1.6 0.8 0 0 3;
33 1.000 0 0 0 3.8 1.9 0 0 3;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]王曹静,顾琨,鲁锴,任延涛.电力系统潮流分析浅析[J].科技信息,2011(24):334-335.
🌈4 Matlab代码实现
相关文章:

电力系统系统潮流分析【IEEE 57 节点】(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
Java——N皇后问题
题目链接 leetcode在线oj题——N皇后 题目描述 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ÿ…...
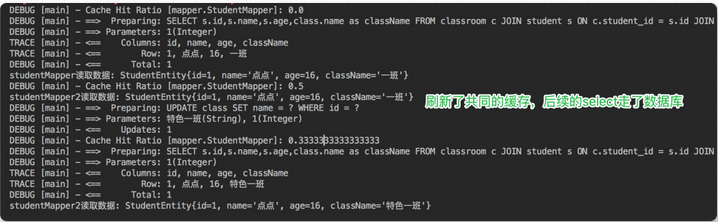
Mybatis一级缓存与二级缓存
一、MyBatis 缓存缓存就是内存中的数据,常常来自对数据库查询结果的保存。使用缓存,我们可以避免频繁与数据库进行交互,从而提高响应速度。MyBatis 也提供了对缓存的支持,分为一级缓存和二级缓存,来看下下面这张图&…...
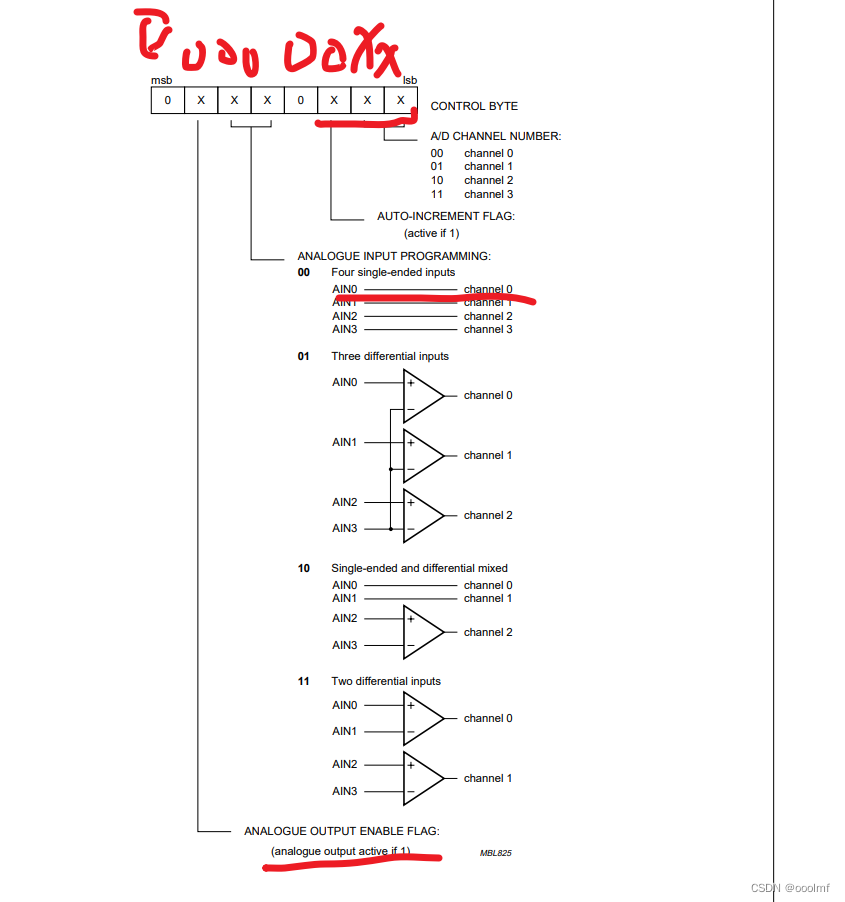
LQB,手打,PCF8591,ADDA转换,AD1是光敏电阻,AD3是电位器,DA输出
在上述at24c02de 基础上,添加三个函数 一个是读取通道1光敏电阻的数据; 一个是读取通道3的电压; 一个是输出DA的数据。。 5V的AD DA。 如果读入的电压是5V,输入AD,就是255; 如果是0V,就是00000…...

【计组笔记06】计算机组成与原理之控制器和总线结构
这篇文章,主要介绍计算机组成与原理之控制器和总线结构。 目录 一、控制器功能 1.1、控制器组成 1.2、控制单元的输入和输出...

elisp简单实例: auto-save
elisp 能找一个简单又实用的代码很不容易,以下代码不是我的原创,只是结合自己的理解,添加修正了一些注释,荣誉归原作者,感谢原作者的开源精神! 调用说明: 把后面代码存为auto-save.el 在init.el 中写上 (require auto-save) 就可以了. 下面是auto-save.el 内容了. ;; 我…...

写字楼/园区/购物中心空置率太高?快用快鲸智慧楼宇系统
客户租不租你的写字楼,事关区位、交通、环境、价格、面积、装修等诸多因素,但很多招商部对这些影响客户决策的数据并不重视,在客户初次上门看房时仅简单记录姓名、联系方式、需求面积,对其他核心数据熟视无睹,也为日后…...
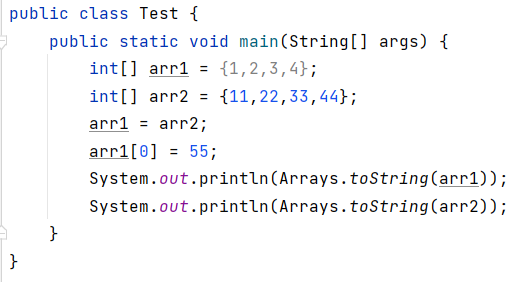
【JavaSE】数组的定义和使用(上)
数组的定义和使用(上)6-数组的定义与使用1. 数组的基本概念1.1 为什么要使用数组1.2 什么是数组1.3 数组的创建及初始化1.3.1 数组的创建1.3.2 数组的初始化1.4 数组的使用1.4.1 数组中元素的访问1.4.2 遍历数组2. 数组是引用类型2.1 初始JVM的内存分布2…...

计算机的学习路线
本文是介绍如何成为一个Geek,一个真正的计算机高手。 适合有成为IT领域技术大牛的人参考。 写给大一新生和所有向深耕IT领域的人,避免走一些弯路。 第一门入门的必备功课-语法与算法 什么是计算机? 用来做运算的机器 电子计算机在运算方面…...

TD算法超详细解释,一篇文章看透彻!
【已解决】TD算法超详细解释和实现(Sarsa,n-step Sarsa,Q-learning)一篇文章看透彻! 郑重声明:本系列内容来源 赵世钰(Shiyu Zhao)教授的强化学习数学原理系列,本推文出于非商业目的分享个人学习…...
4.1 路由器(华硕 官改/梅林 华为 小米 路由) 使用花生壳 实现远程管理
最近添置了一台华硕的八爪鱼GT AC5300,到手后刷了官改,而里面软件中就提供了花生壳程序,想到花生壳为每个用户提供了两条免费映射(带宽为1mbs,流量为1g/月),所以就打算利用来做一个远程访问。具…...
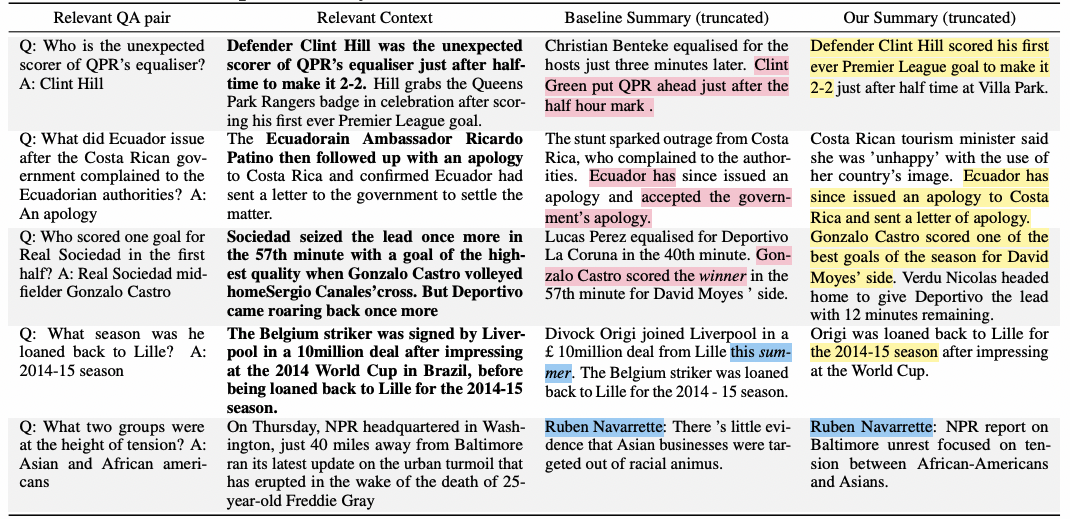
内容算法解读:提高内容摘要与原文的一致性(Faithfulness)
全文摘要:受益于预训练语言模型的发展,应用神经网络模型提取内容摘要的技术也获得了长足进步。但目前还存在一个未被很好解决的问题:神经网络模型提取的摘要不能如实反映原文档的中心思想,没有做到忠实(not faithful&a…...

python用openpyxl包操作xlsx文件,统计表中合作电影数目最多的两个演员
题目🎉🎉🎉:编程完成下面任务:已知excel文件“电影导演演员信息表.xlsx”如下图所示:🍳🍳🍳要求:使用 openpyxl 包操作打开此文件,编写程序统计在…...

Lesson12---人工神经网络(1)
12.1 神经元与感知机 12.1.1 感知机 感知机: 1957, Fank Rosenblatt 由两层神经元组成,可以简化为右边这种,输入通常不参与计算,不计入神经网络的层数,因此感知机是一个单层神经网络 感知机 训练法则&am…...
)
算法练习-排序(二)
算法练习-排序(二) 文章目录算法练习-排序(二)1 合并排序的数组1.1 题目1.2 题解2 有效的字母异位词2.1 题目2.2 题解3 判断能否形成等差数列3.1 题目3.2 题解4 合并区间4.1 题目3.2 题解5 剑指 Offer 21. 调整数组顺序使奇数位于偶数前面5.1 题目5.2 题解6 颜色分类6.1 题目6.…...

202302读书笔记|《长安的荔枝》——只要肯努力,办法总比困难多
202302读书笔记|《长安的荔枝》——只要肯努力,办法总比困难多 《长安的荔枝》这本书真是酣畅淋漓啊,读起来一气呵成,以讲故事的口吻叙述,上林署九品小官员——李善德,兢兢业业工作多年,终于借贷买了房&…...
java封装继承多态详解
1.封装 所谓封装,就是将客观事物封装成抽象的类,并且类可以把数据和方法让可信的类或者对象进行操作,对不可信的类或者对象进行隐藏。类就是封装数据和操作这些数据代码的逻辑实体。在一个类的内部,某些属性和方法是私有的&#…...
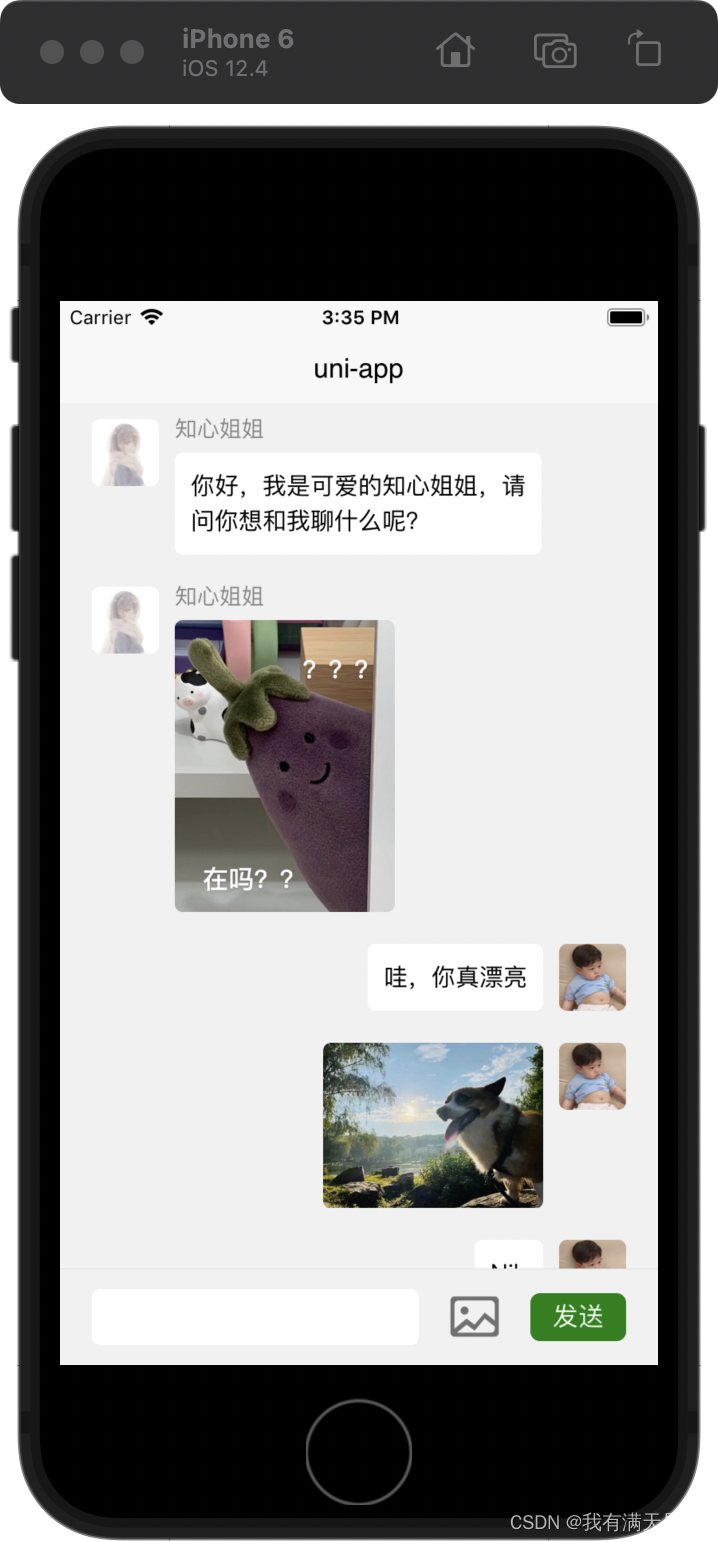
【uni-app教程】UniAPP 常用组件和 常用 API 简介# 知心姐姐聊天案例
五、UniAPP 常用组件简介 uni-app 为开发者提供了一系列基础组件,类似 HTML 里的基础标签元素,但 uni-app 的组件与 HTML 不同,而是与小程序相同,更适合手机端使用。 虽然不推荐使用 HTML 标签,但实际上如果开发者写了…...
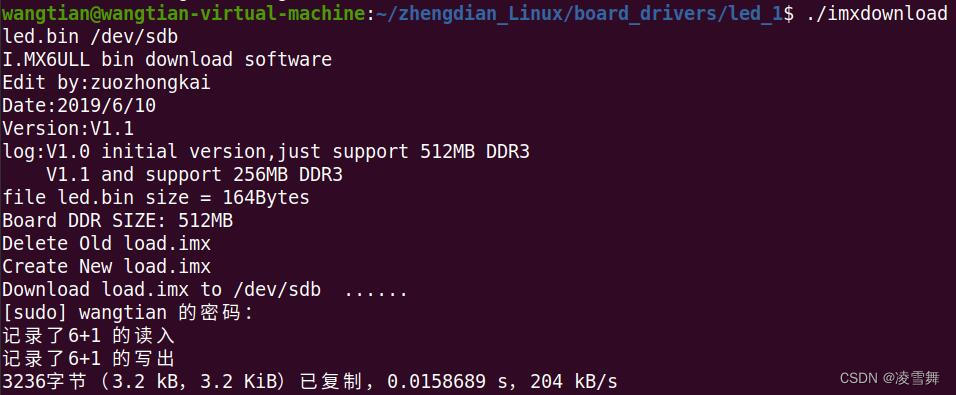
阿尔法开发板 .bin 文件烧写
一. IMX6ULL 开发板简介 IMX6ULL 开发板是正点原子提供的阿尔法开发板,所用芯片为恩智浦,基于 Cortex-A7 架构。 这里介绍一下裸机篇中,关于如何将 .bin 文件烧写进 SD 卡,从而设备运行程序。 二. xx.bin 文件烧写 IMX6ULL支…...
Ceres-Solver 安装与卸载ubuntu20.04
卸载 sudo rm -rf /usr/local/lib/cmake/Ceres /usr/local/include/ceres /usr/local/lib/libceres.a 安装 sudo apt-get install libatlas-base-dev libsuitesparse-dev git clone https://github.com/ceres-solver/ceres-solver cd ceres-solver git checkout $(git descr…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...
