LeetCode---380周赛
题目列表
3005. 最大频率元素计数
3006. 找出数组中的美丽下标 I
3007. 价值和小于等于 K 的最大数字
3008. 找出数组中的美丽下标 II
一、最大频率元素计数

这题就是个简单的计数题,正常遍历统计数据即可,关键是你要会写代码逻辑。
代码如下(如果代码看不懂的,建议按照代码逻辑手动模拟几次)
//两次遍历
class Solution {
public:int maxFrequencyElements(vector<int>& nums) {unordered_map<int,int>mp;for(auto&e:nums) mp[e]++;int sum=0,mx=0;for(auto it=mp.begin();it!=mp.end();++it){if(mx<it->second){sum=it->second;mx=it->second;}else if(mx==it->second){sum+=mx;}}return sum;}
};//一次遍历
class Solution {
public:int maxFrequencyElements(vector<int>& nums) {int mx=0,s=0;unordered_map<int,int>cnt;for(auto x:nums){cnt[x]++;if(cnt[x]>mx){s=mx=cnt[x];}else if(cnt[x]==mx){s+=mx;}}return s;}
};二、找出数组中的美丽下标I&II

这题就按照题目说的去模拟就行,关键是优化时间复杂度,当然这题暴力也可以过,但是第四题就不行了。这里先用暴力去写。
简单说一下思路:先分别找出字符串a、b在s中可以匹配的位置,放到两个数组中,然后再找出符合条件的字符串a的下标,最后返回答案即可
代码如下
class Solution {vector<int> Get(string& s,string& a){vector<int>v;size_t pos=s.find(a);while(pos!=string::npos){v.push_back(pos);pos=s.find(a,pos+1);}return v;}
public:vector<int> beautifulIndices(string s, string a, string b, int k) {int n=s.size();vector<int>va=Get(s,a);vector<int>vb=Get(s,b);vector<int>ans;for(int i=0;i<va.size();i++){for(int j=0;j<vb.size();j++){if(abs(va[i]-vb[j])<=k){ans.push_back(va[i]);break;}}}return ans;}
};如何优化时间复杂度?
在上面的代码中,代码的逻辑有两个模块:1、字符串匹配 2、找符合条件的下标
针对上面的两个模块,我们的优化方案如下
1、对字符串匹配的优化---KMP算法---这个后面会出文章具体讲该算法的原理,这里就不细说了
2、找符合条件的下标,我们的暴力写法没有用到两个数组有序的条件,一般来说,数组有序都可以有优化的方法,这里就可以用双指针,操作和原理如下
设 i 和 j 为va、vb数组的下标
1、va[ i ] < vb[ j ]
- vb[ j ] - va[ i ] <= k 满足条件,将va[i]加入答案,i++,j不用加,因为vb[ j ]有可能让va[i+1]也符合条件
- vb[ j ] - va[ i ] > k 不满足条件,i++,因为vb[j]后面的数只会离va[i]最来越远,i不可能在满足条件,j不用加,因为vb[ j ]有可能让va[i+1]也符合条件
2、va[ i ] >= vb[ j ]
- va[ i ] - vb[ j ] <= k 满足条件,将va[i]加入答案,i++,j不用加,因为vb[ j ]有可能让va[i+1]也符合条件
- va[ i ] - vb[ j ] > k 不满足条件,j++,i不变,因为vb[ j + 1] 可能离va[ i ]更近
双指针的本质就是让va[ i ]尽可能地与它相隔最近的vb[ j ]比较,从而避免一些没有必要的比较,在上面的遍历过程中只有i++和j++,时间复杂度为O(m+n)(m、n为两个数组的大小)
当然用二分查找也能优化,但是双指针更快。
代码如下(双指针+KMP)
class Solution {//KMPvector<int> Get(string& s,string& a){int n=a.size();vector<int>next(n);for(int i=1,j=0;i<n;i++){while(j&&a[j]!=a[i])j=next[j-1];if(a[j]==a[i])j++;next[i]=j;}vector<int>ret;for(int i=0,j=0;i<s.size();i++){while(j&&s[i]!=a[j])j=next[j-1];if(s[i]==a[j])j++;if(j==n){ret.push_back(i-n+1);j=next[j-1];}}return ret;}
public:vector<int> beautifulIndices(string s, string a, string b, int k) {vector<int>va=Get(s,a);vector<int>vb=Get(s,b);vector<int>ans;int n=va.size(),m=vb.size();int i=0,j=0;while(i<n&&j<m){if(va[i]<vb[j]){if(vb[j]-va[i]<=k)ans.push_back(va[i]);i++;}else{if(va[i]-vb[j]<=k){ans.push_back(va[i]);i++;}else{j++;}}}return ans;}
};三、价值和小于等于K的最大数字

题目中出现小于等于求最大,一般是用二分 (对二分不了解的可以看看我之前写的二分查找详解),下面我们来分析一下,是否能用二分来做?即是否具有单调性。我们知道 num 越大,整数的价值和就会越大, 两者成正比,满足单调性,那么就能用二分来做。
(二分的上下界选择问题:一般我们选0为下界,选一个极大值作为上界,让答案在区间内即可,如果你想要更为精确的上下界,这里也简单说明一下,0为下界没什么好说的,那么这个上界怎么得到呢?这题可以这么想,我们只求每个整数第x位上的1,需要的数字为多少?[ 低于x的位不考虑 因为我们取的是一个区间,并不要求准确 ] 是 k<<x <=> k*2^x )
现在关键在于如何判断 [1,num] 区间内的整数价值和是否满足条件,即如何求该区间的价值和?
这里有两种做法:1、数位dp(暴力) 2、找数学规律
数位dp上周才写过,套路都差不多,这里就不多介绍了,代码如下
class Solution {typedef long long LL;
public:LL check(LL n,int x){//下面写的数位dp是从高位到低位枚举二进制//当然你也可以将n处理得到它的二进制字符串,都是可以的int m=64-__builtin_clz(n);vector<vector<LL>>memo(m,vector<LL>(m+1,-1));function<LL(int,int,bool)>dfs=[&](int i,int j,bool limit_high)->LL{if(i<0)return j;if(!limit_high&&memo[i][j]!=-1) return memo[i][j];LL res=0;int up=limit_high?(n>>i)&1:1;for(int d=0;d<=up;d++)res+=dfs(i-1,j+(d==1&&(i+1)%x==0),limit_high&&up==d);if(!limit_high)memo[i][j]=res;return res;};return dfs(m-1,0,true);}long long findMaximumNumber(long long k, int x) {LL l=0,r=k<<x;while(l<=r){LL mid=l+(r-l)/2;if(check(mid,x)<=k)//二分的判断条件 l=mid+1;else r=mid-1;}return r;}
};下面来讲讲数学规律
题目要求特定二进制位上的1的个数,那么我们是不是可以看看这些特定二进制位对1的贡献,然后将贡献相加得到1的个数,解析如下

class Solution {typedef long long LL;
public:LL check(LL n,int x){LL ans=0;int i=x-1;for(LL y = n>>i; y; y>>=x,i+=x){ans+=(y/2)<<i;//求[1,(n>>i)-1]的奇数个数if(y%2){// LL mask=(1LL<<i)-1;// ans+=(n&mask)+1;//注意这里是nLL mod=1LL<<i;ans+=n%mod+1;//注意这里是n}}return ans;}long long findMaximumNumber(long long k, int x) {LL l=0,r=k<<x;while(l<=r){LL mid=l+(r-l)/2;if(check(mid,x)<=k) l=mid+1;else r=mid-1;}return r;}
};相关文章:

LeetCode---380周赛
题目列表 3005. 最大频率元素计数 3006. 找出数组中的美丽下标 I 3007. 价值和小于等于 K 的最大数字 3008. 找出数组中的美丽下标 II 一、最大频率元素计数 这题就是个简单的计数题,正常遍历统计数据即可,关键是你要会写代码逻辑。 代码如下&…...

archlinux 如何解决安装以后没有声音的问题
今天安装完archlinux以后发现看视频没声音 检查一下是否有 /lib/firmware/intel/sof 发现没有 如果你也是这样的话,可以尝试安装: sudo pacman -S sof-firmware 重启后再看看有没有声音: reboot 反正我有声音了...

什么是ORM思想?
1. ORM概念 ORM(Object Relational Mapping)对象关系映射模式,是一种技术,解决了面向对象与关系型数据库存互不匹配的现象。 ORM在业务逻辑层和数据库层之间充当了桥梁的作用。 2. ORM由来 在软件开发的过程中,通常…...

设计接口时,为其添加签名鉴权---详细教程
一、何为签名 我们知道无论是restful api还是传统接口、亦或是其他形式接口的调用,接口签名都是非常重要的安全机制,它可以确保请求的发起者是经过认证和授权的客户端,同时也可以防止接口被攻击,请求参数被篡改等等。 用大白话来解…...
5G+物联网:连接万物,重塑智慧社区,开启未来生活新纪元,助力智慧社区的革新与发展
一、5G与物联网:技术概述与基础 随着科技的飞速发展,第五代移动通信技术(5G)和物联网(IoT)已经成为当今社会的热门话题。这两项技术作为现代信息社会的核心基础设施,正深刻地改变着人们的生活和…...
[反转链表] [合并两个有序链表][分割链表]
这里写目录标题 反转链表合并两个有序链表分割链表 反转链表 1、题目: 2.思路 思路1:建立一个newHead,取一个节点进行头插。具体做法如下! 建立一个newHead(新头),由于一个节点里面存的是下一个节点的地址,如果取…...
中文数据让LLM变笨?
我这里先贴一下论文的原链接: https://arxiv.org/abs/2401.10286 然后贴一下我翻译标注的下载链接:https://gitee.com/chatpaper/arXiv_top_chinese/blob/master/0801_top/%E4%B8%AD%E6%96%87%E4%BC%9A%E8%AE%A9LLM%E5%8F%98%E7%AC%A8%EF%BC%9F.pdf 先…...
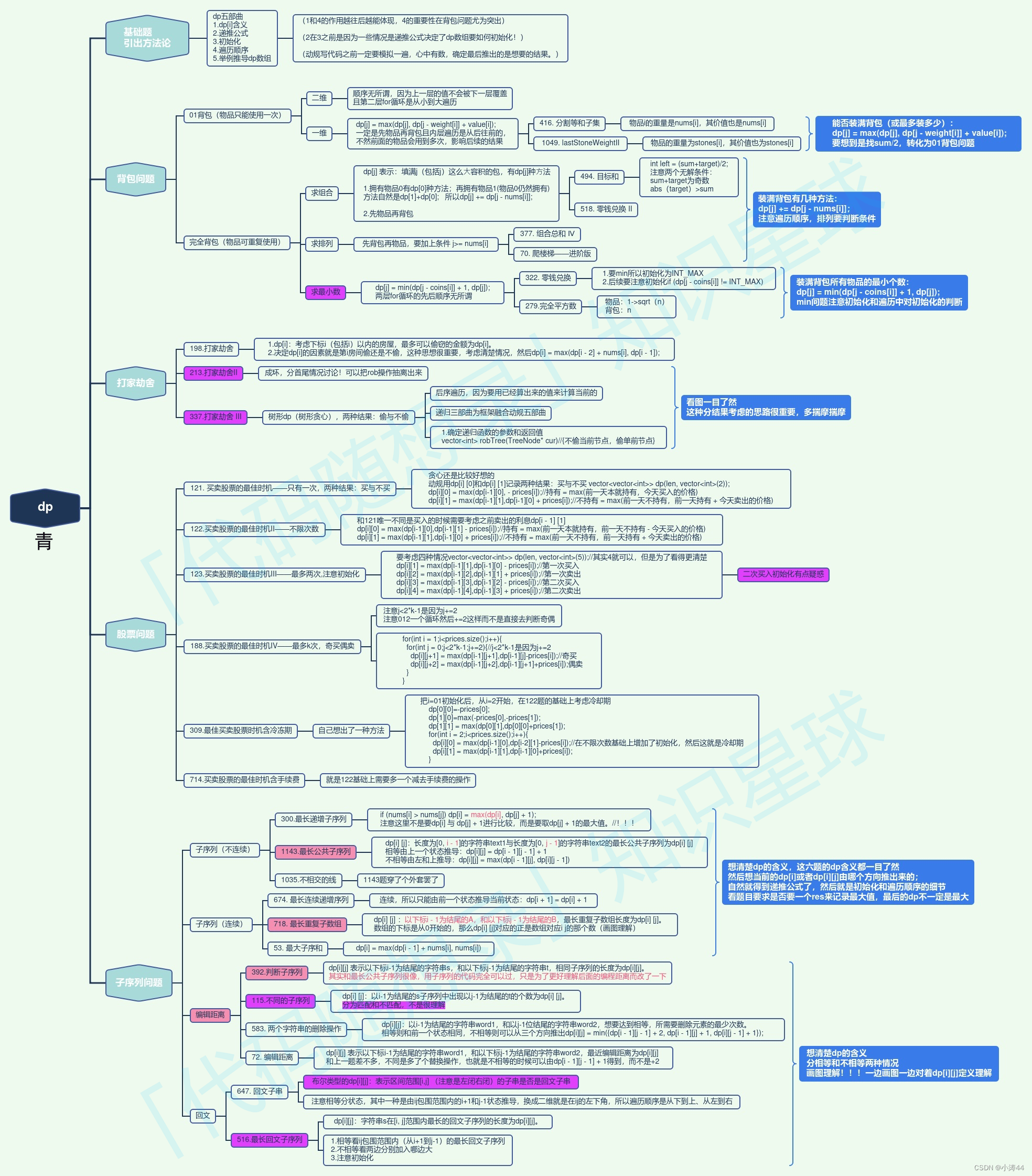
【代码随想录】刷题笔记Day54
前言 差单调栈就结束代码随想录一刷啦,回家二刷打算改用python补充进博客,小涛加油!!! 647. 回文子串 - 力扣(LeetCode) 双指针法 中心点外扩,注意中心点可能有一个元素可能有两个…...
二.Winform使用Webview2在Demo1中实现地址简单校验
Winform使用Webview2在Demo1中实现地址简单校验 往期目录回顾添加对于的简单url验证提示通过上节和本节涉及到的函数有 往期目录 往期相关文章目录 专栏目录 回顾 通过一.Winform使用Webview2(Edge浏览器核心) 创建demo(Demo1)实现回车导航到指定地址 我们已经知道了解决资源…...

从0开始学习C++ 第二十课:模板与泛型编程
第二十课:模板与泛型编程 学习目标: 掌握模板的基本语法和概念。学会使用函数模板来创建可重用的函数。学习如何定义类模板以实现数据结构的泛型。理解模板在C中提供的灵活性和强大功能。 学习内容: 模板的概念: 模板是C中支持…...

pcl之滤波器(一)
pcl滤波器 pcl一共是有十二个主要模块,详细了解可以查看官网。https://pcl.readthedocs.io/projects/tutorials/en/latest/#basic-usage 今天学习一下pcl的滤波器模块。 滤波器模块,官网一共是提供了6个例程,今天先来看第一第二个。 直通…...
)
java项目性能优化(MyBatis中开启查询缓存及flushCache与useCache的使用)
在java项目中,如果需要大量的DB查询,导致缓存过多,项目运行缓慢,可以设置在select查询时,添加二级缓存的清空。 如果没有去配置flushCache、useCache,那么默认是启用缓存的。 1,flushCache默认…...
Unity3D控制人物移动的多种方法
系列文章目录 unity知识点 文章目录 系列文章目录前言一、人物移动之键盘移动1-1、代码如下1-2、效果 二、人物移动之跟随鼠标点击移动2-1、代码如下2-2、效果 三、人物移动之刚体移动3-1、代码如下3-2、效果 四、人物移动之第一人称控制器移动4-1、代码如下4-2、效果 五、And…...

无人机打击激光器
激光器的应用非常广泛,涵盖了多个领域。以下是一些主要的激光器应用: 医疗领域:激光器在医疗行业中有着重要应用,比如用于激光手术(如眼科手术)、皮肤治疗、牙科治疗、肿瘤治疗等。 工业制造:在…...

Lingo数学建模基础
1.基本运算符 1.1算数运算符 1.2逻辑运算 #not# 否定操作数的逻辑值,一元运算符 #eq# 若两运算数相等,则为true,否则为false #ne# 若两运算数不相等,则为true,否则为false #gt# 若左边运算数严格大于右边,则为true,否则为…...
finalshell连接linux的kali系统
kali的ssh服务似乎是默认关闭的,笔者在玩CentOS系统时可以直接用finalshell完成连接,但kali不行,需要先手动开启ssh服务。 开启kali的ssh服务 输入【ssh start】命令开启ssh服务,可以用【ssh status】命令查看ssh状态,…...

2、Line Charts折线图
可视化时间趋势 现在你已经熟悉了编码环境,是时候学习如何制作自己的图表了! 在本教程中,您将学习足够的Python来创建专业外观的折线图。然后,在接下来的练习中,您将使用您的最新技能处理真实世界的数据集。 本课程数据集夸克网盘下载链接:https://pan.quark.cn/s/a235ac…...
)
shell脚本获得所有数据库备份(整库备份,表级备份)
数据库备份到天翼云对象存储OBS https://blog.csdn.net/qq_34631220/article/details/135755894 1、获得所有数据库 #!/bin/sh HOSTNAME"ip" #数据库信息 PORT"3306" USERNAME"root" PASSWORD"" DBNAME"yusuan" #数据库…...
REVIT二次开发万能刷
将这两个参数赋予其他参数 步骤2 将来做个可以调控的版本 using System; using System.Collections.Generic; using System.Lin...

JSON简单了解
文章目录 1、JSON介绍2、ES6模版字符串3、JS对象转化为JSON字符串3.1、手动JS对象转化为JSON字符串3.2、自动JS对象转化为JSON字符串 4、JS对象和java互相转换 1、JSON介绍 JSON 概念:JavaScript Object Notation。JavaScript 对象表示法,简单理解JSON是…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
