数据结构<1>——树状数组
树状数组,也叫Fenwick Tree和BIT(Binary Indexed Tree),是一种支持单点修改和区间查询的,代码量小的数据结构。
那神马是单点修改和区间查询?我们来看一道题。
洛谷P3374(模板): 在本题中,单点修改就是将某一个数加上x的操作,区间查询就是求出某区间每一个数的和的操作,这下明白了吧。
下面来解释一下树状数组的工作原理。先看一张图(来源于OI-Wiki)
Tips:别找了,点一下"图"那个字就有了。
我们发现,树状数组总能将一段前缀拆成不多于段区间,使得这几段区间的信息是已知的。因此,我们只用合并这些区间的信息,就可以得到答案。因此,时间复杂度从
变成
,效率大大提高。
管辖区间
我们观察刚刚的图发现,每个相当于一个小leader,掌管自己的范围。那这个范围是多少呢?我们规定
管辖的区间长度为
,其中k为x的二进制表示中,最低位的1所在的二进制位数。而
为x的二进制表示中,最低位的1以及后面所有0组成的数。即
管辖的区间是
。注意:lowbit(x)表示这个1和后面所有0组成的
。
下面附上OI-Wiki中对lowbit(x)的原理的解释(其实是我不会解释)
将 x 的二进制所有位全部取反,再加 1,就可以得到 -x 的二进制编码。例如,![]() 的二进制编码是
的二进制编码是 110,全部取反后得到 001,加 1 得到 010。
设原先 x 的二进制编码是 (...)10...00,全部取反后得到 [...]01...11,加 1 后得到 [...]10...00,也就是 -x 的二进制编码了。这里 x 二进制表示中第一个 1 是 x 最低位的 1。
(...) 和 [...] 中省略号的每一位分别相反,所以 x & -x = (...)10...00 & [...]10...00 = 10...00,得到的结果就是 lowbit。
//lowbit的实现
int lowbit(int x){return x&(-x);
}lowbit可以说是一个很经典的二进制运算了。
区间查询
经过上面的分析,我们可以知道回答区间查询的步骤了:
· 从往前跳,一直让
就行了。
· 如果x=0就结束循环
· 将跑到的累加
实现如下↓:
int get_sum(int x){int sum=0;while(x>0){sum+=c[x];x-=lowbit(x);}return sum;
}单点修改
也很简单。
· 先修改
· 然后一直让让
· 如果x=n就结束循环
实现如下↓:
void modify(int x,int y){while(x<=n){c[x]+=y;x+=lowbit(x);}
}洛谷P3374(模板):
那这题就很easy啦~
#include <bits/stdc++.h>
using namespace std;
int c[maxn];
int n,m;
int lowbit(int x){return x&(-x);
}
void modify(int x,int y){while(x<=n){c[x]+=y;x+=lowbit(x);}
}
int get_sum(int x){int res=0;while(x>0){res+=c[x];x-=lowbit(x);}return res;
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){int x;cin>>x;modify(i,x);}for(int i=1;i<=m;i++){int op,x,y;cin>>op>>x>>y;if(op==1)modify(x,y);if(op==2)cout<<get_sum(y)-get_sum(x-1)<<endl;}return 0;
}别走啊,这不得在找几题练练?
逆序对:
基础题。现在按照序列从左到右将数据的值对应的位置的数加一,代表又有一个数出现。因此,在循环到第i项时,前i-1项已经加入到树状数组内了,树状数组内比大的都会与
构成逆序对,因为它们一定出现的更早,所以产生的逆序对数量为
。要注意的是,我们需要进行离散化,因为根据
建树确实不够。然后就是代码部分啦。
#include <bits/stdc++.h>
using namespace std;
pair<long long,long long> a[maxn];
long long b[maxn],c[maxn];
int n;
int lowbit(int x){return x&(-x);
}
void modify(int x){while(x<=n){c[x]++;x+=lowbit(x);}
}
int get_sum(int x){int sum=0;while(x>0){sum+=c[x];x-=lowbit(x);}return sum;
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i].first;a[i].second=i;}sort(a+1,a+n+1);for(int i=1;i<=n;i++)b[a[i].second]=i;long long ans=0;for(int i=n;i;i--){ans+=get_sum(b[i]);modify(b[i]);}cout<<ans<<endl;return 0;
}当然,用归并也是Ok的。
火柴排队:
一道非常非常经典的题目。我们乍一看,就是让我们最小化,也就是最小化
,也就是a序列第k大的元素必须和序列b中第k大的元素
的位置必须一样。OK,那我们把a,b离散化,问题变成了b序列要交换几次可以令其等于a。我们令
,相当于以
为关键字对序列
排序,如果a和b一样,那么
。那么我们需要让q升序排列。问题又变成,将原本乱的 q序列升序排列的最少交换次数。
诶,这不就是逆序对吗?
用树状数组或归并即可。这里给归并的代码,树状数组的参考上面P1908的代码。
#include <bits/stdc++.h>
using namespace std;
int a[maxn],b[maxn];
int c[maxn],d[maxn];
int num1[maxn],num2[maxn];
int calc[maxn];
long long ans=0;
int tmp[maxn];
void msort(int l,int r){if(l==r)return;int mid=(l+r)>>1;msort(l,mid);msort(mid+1,r);int i=l,j=mid+1;int k=l;while(i<=mid && j<=r){if(a[i]<=a[j])tmp[k++]=a[i++];else{tmp[k++]=a[j++];ans+=mid-i+1;ans%=MOD;}}while(i<=mid)tmp[k++]=a[i++];while(j<=r)tmp[k++]=a[j++];for(int i=l;i<=r;i++)a[i]=tmp[i];
}
int main(){int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];c[i]=a[i];}for(int i=1;i<=n;i++){cin>>b[i];d[i]=b[i];}sort(d+1,d+n+1);for(int i=1;i<=n;i++)num1[d[i]]=i;sort(c+1,c+n+1);for(int i=1;i<=n;i++)num2[c[i]]=i;for(int i=1;i<=n;i++)calc[num1[b[i]]]=i;for(int i=1;i<=n;i++)a[i]=calc[num2[a[i]]];msort(1,n);cout<<ans%MOD<<endl;return 0;
}别忘了取模哦。
The Last Problem:ABC157E
此题一看就是树状数组。但是由于有26个字母,我们要建26个树状数组,每一个存放该字母出现的位置。这样,在询问的时候,直接查询每一个树状数组的[l,r]的和,如果这个和>0,那么就把 ans加1,最后输出即可。
#include <bits/stdc++.h>
using namespace std;
int c[26][500005];
int lowbit(int x){return x&(-x);
}
void update(int c[],int x,int val){while(x<=500000){c[x]+=val;x+=lowbit(x);}
}
int getsum(int c[],int x){int sum=0;while(x>0){sum+=c[x];x-=lowbit(x);}return sum;
}
int main(){int n;cin>>n;string str;cin>>str;str=' '+str;for(int i=1;i<=n;i++)update(c[str[i]-'a'],i,1);int q;cin>>q;while(q--){int op;cin>>op;if(op==1){int x;char ch;cin>>x>>ch;update(c[str[x]-'a'],x,-1);update(c[ch-'a'],x,1);str[x]=ch;}if(op==2){int l,r;cin>>l>>r;int ans=0;for(int i=0;i<26;i++){if(getsum(c[i],r)-getsum(c[i],l-1))ans++;}cout<<ans<<endl;}}return 0;
}Ok,以上就是本期的全部内容了。我们下期再见!
温馨提示:本期的所有代码都有问题,请不要无脑Ctrl C+Ctrl V(你会挂的很惨),看懂了自己写一遍
相关文章:
数据结构<1>——树状数组
树状数组,也叫Fenwick Tree和BIT(Binary Indexed Tree),是一种支持单点修改和区间查询的,代码量小的数据结构。 那神马是单点修改和区间查询?我们来看一道题。 洛谷P3374(模板): 在本题中,单点修改就是将某一个数加上…...
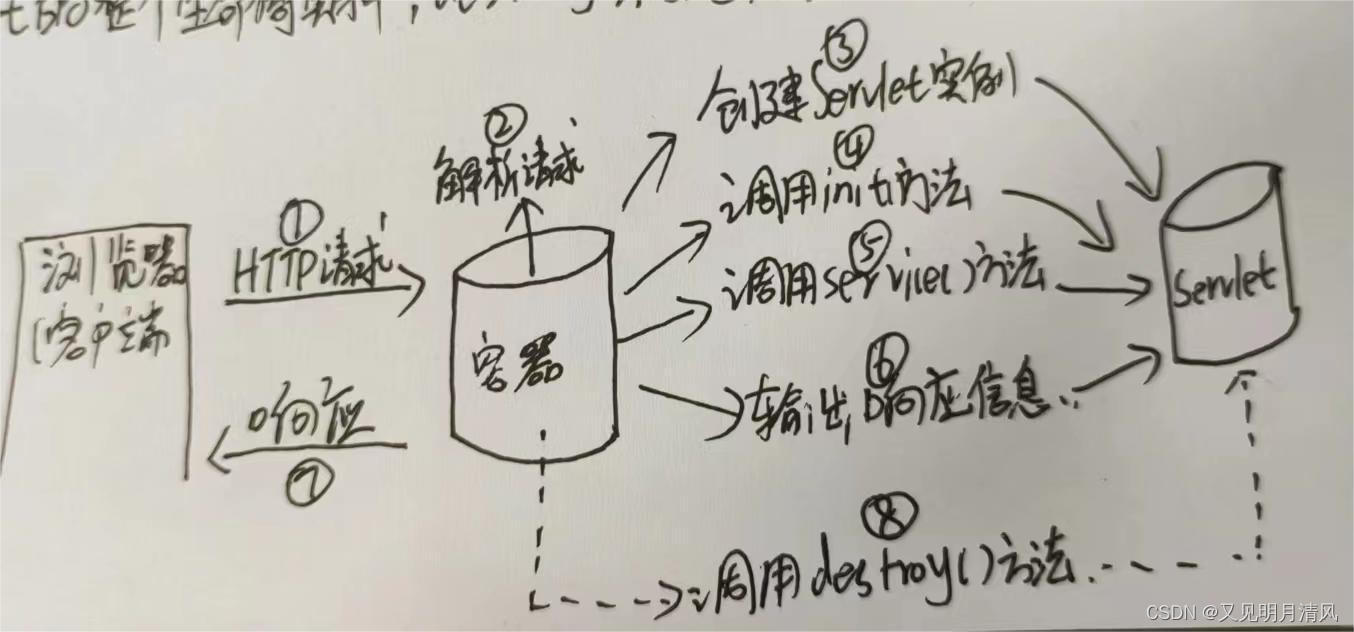
Servlet生命周期
第一阶段: init()初始化阶段 当客户端想Servlet容器(例如Tomcat)发出HTTP请求要求访问Servlet时,Servlet容器首先会解析请求,检查内存中是否已经有了该Servlet对象,如果有ÿ…...
npm i 报一堆版本问题
1,先npm cache clean --force 再下载 插件后缀加上 --legacy-peer-deps 2, npm ERR! code CERT_HAS_EXPIRED npm ERR! errno CERT_HAS_EXPIRED npm ERR! request to https://registry.npm.taobao.org/yorkie/download/yorkie-2.0.0.tgz failed, reason…...

Linux设备管理模型-01:基础数据结构
文章目录 1. 设备管理模型2. 基本数据结构2.1 kobject2.2 kset 1. 设备管理模型 设备模型是内核提供的一个编写驱动的架构。 设备管理是设备-总线-驱动结构。 linux中的设备是由树状模型组织的,从sysfs中可以查看树状结构。 他本身实现了: 电源管理热…...
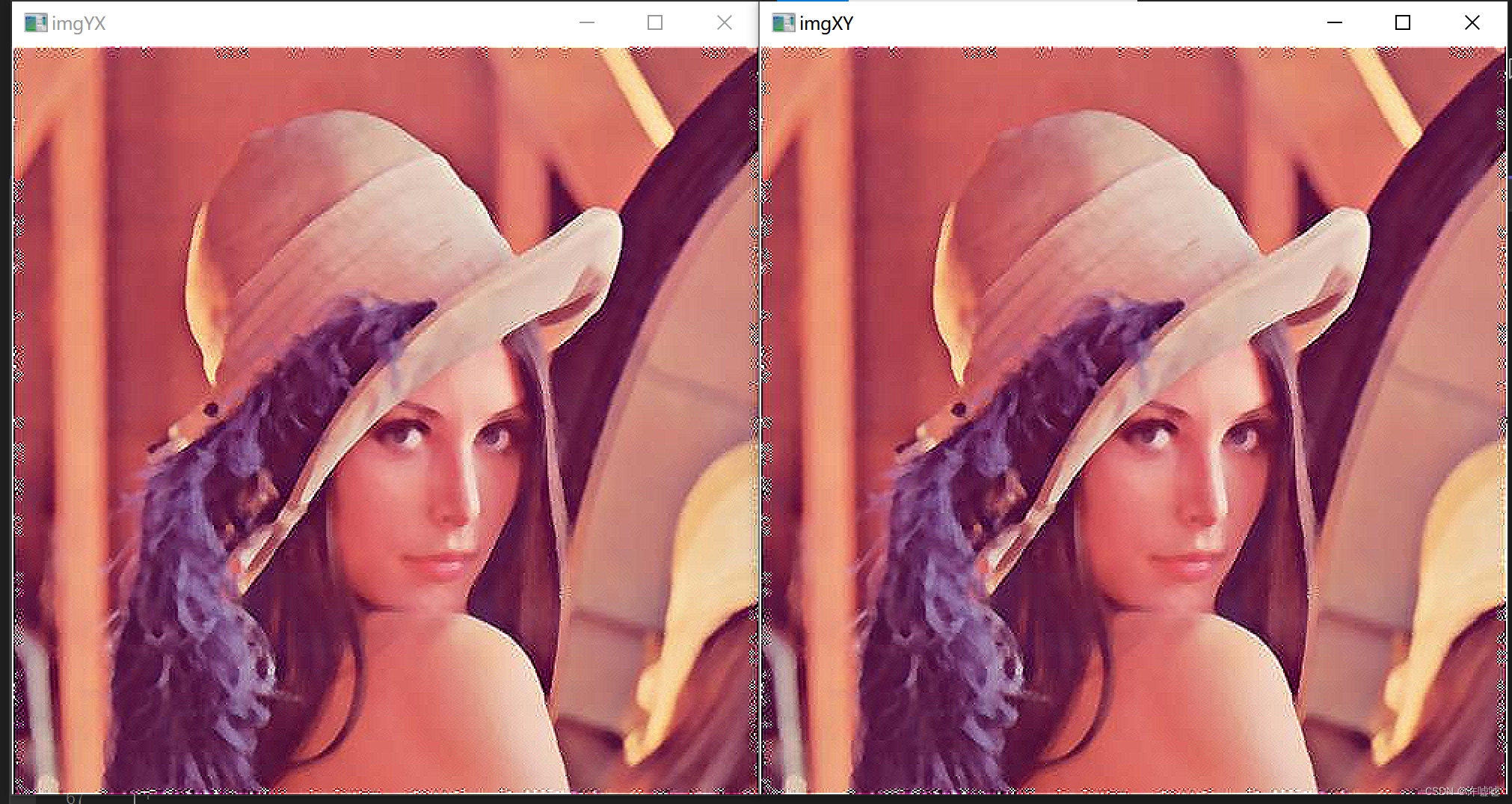
opencv#32 可分离滤波
滤波的可分离性 就是将一个线性滤波变成多个线性滤波,这里面具体所指的是变成x方向的线性滤波和y方向的线性滤波。无论先做x方向的滤波还是y方向滤波,两者的叠加结果是一致的,这个性质取决于滤波操作是并行的,也就是每一个图像在滤…...

android 导航app 稳定性问题总结
一 重写全局异常处理: 1 是过滤掉一些已知的无法处理的 问题,比如TimeoutException 这种无法根除只能缓解的问题可以直接catch掉 2 是 一些无法继续的问题可以直接杀死重启,一些影响不是很大的,可以局部还原 比如: p…...
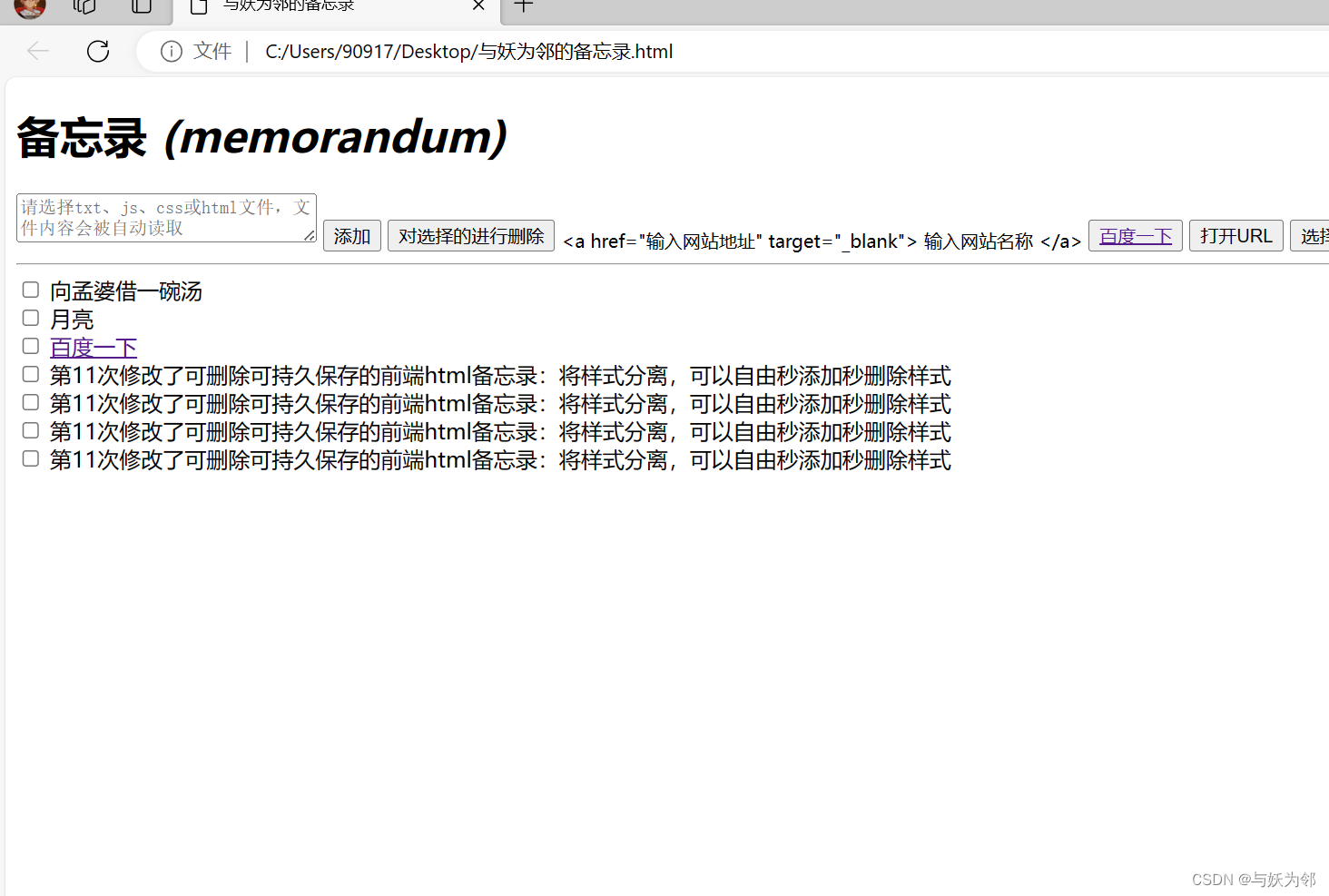
第11次修改了可删除可持久保存的前端html备忘录:将样式分离,可以自由秒添加秒删除样式
第11次修改了可删除可持久保存的前端html备忘录:将样式分离,可以自由秒添加秒删除样式 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"…...
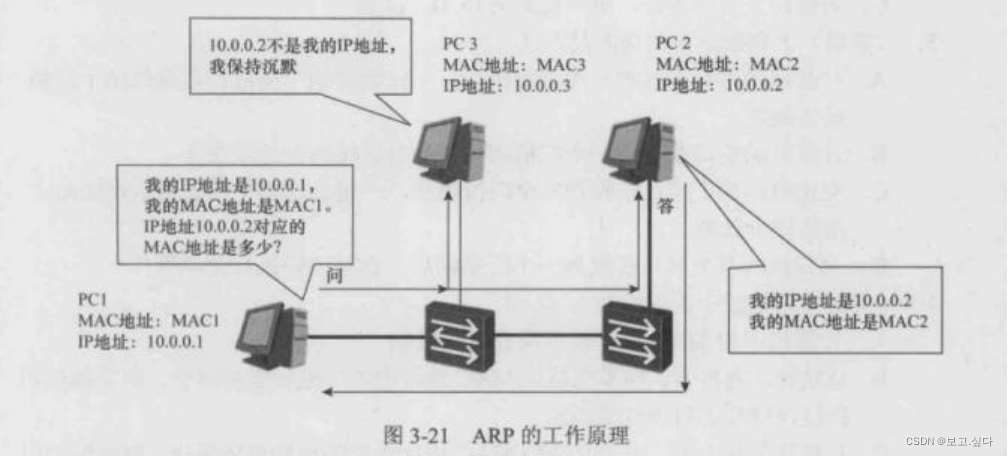
hcip高级网络知识
一:计算机间信息传递原理 抽象语言----编码 编码---二进制 二进制---转换为电流(数字信号) 处理和传递数字信号 二:OSI--七层参考模型 ISO--1979 规定计算机系统互联的组织: OSI/RM ---- 开放式系统互联参考模型 --- 1…...
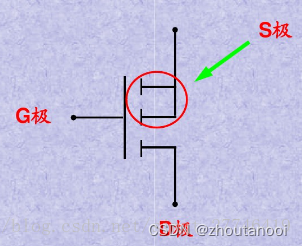
常用电子器件学习——MOS管
MOS管介绍 MOS,是MOSFET的缩写。MOSFET 金属-氧化物半导体场效应晶体管,简称金氧半场效晶体管(Metal-Oxide-Semiconductor Field-Effect Transistor, MOSFET)。 一般是金属(metal)—氧化物(oxide)—半导体(semiconductor)场效应晶…...

System.Data.SqlClient.SqlException:“在与 SQL Server 建立连接时出现与网络相关的或特定于实例的错误
目录 背景: 过程: SQL Express的认识: 背景: 正在运行程序的时候,我遇到一个错误提示,错误信息如下,当我将错误信息仔细阅读了一番,信息提示的很明显,错误出现的来源就是连接数据库代码这块string connStr "s…...
)
数据库(SQL语句:DMLDQL)
目录 有关数据表的DML操作 1.1 INSERT 语句 1.2 REPLACE 语句 replace语句的语法格式(三种) REPLACE 语句 和 INSERT 语句的区别 1.3 DELETE 语句 | | TRUNCATE 语句 DELETE TRUNCATE DROP 1.4 UPDATE 数据 1.5 SELECT 语句 (DQL数…...

AnimatedDrawings:让绘图动起来
老样子,先上图片和官网。这个项目是让绘制的动画图片动起来,还能绑定人体的运动进行行为定制。 快速开始 1. 下载代码并进入文件夹,启动一键安装 git clone https://github.com/facebookresearch/AnimatedDrawings.gitcd AnimatedDrawingspip…...
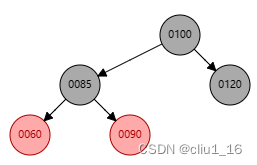
红黑树浅浅学习
红黑树浅浅学习 红黑树概念红黑树平衡性调整 红黑树概念 二叉树:二叉树是每个节点最多有两个子树的树结构。二叉查找树:又称“二叉搜索树”,左孩子比父节点小,右孩子比父节点大,还有一个特性就是”中序遍历“可以让结…...

QGraphicsView 如何让图形大小适配窗口
1. setSceneRect 做什么用? setSceneRect是一个Qt中的函数,用于设置QGraphicsView中的场景矩形(QRectF)。 QGraphicsView是一个用于显示和编辑图形场景的控件,而setSceneRect函数用于设置场景矩形,即指定…...

sqlmap使用教程(3)-探测注入漏洞
1、探测GET参数 以下为探测DVWA靶场low级别的sql注入,以下提交方式为GET,问号(?)将分隔URL和传输的数据,而参数之间以&相连。--auth-credadmin:password --auth-typebasic (DVWA靶场需要登录…...

期待已久!阿里云容器服务 ACK AI 助手正式上线
作者:行疾 大模型技术的蓬勃发展持续引领 AI 出圈潮流,各行各业都在尝试采用 AI 工具实现智能增效。 2023 年云栖大会上,阿里云容器服务团队正式发布 ACK AI 助手,带来大模型增强智能诊断,帮助企业和开发者降低 K8s …...
[BUG] Authentication Error
前言 给服务器安装了一个todesk,但是远程一直就是,点击用户,进入输入密码界面,还没等输入就自动返回了 解决 服务器是无桌面版本,或者桌面程序死掉了,重新安装就好 sudo apt install xorg sudo apt inst…...

23种设计模式概述
学习设计模式对我们有什么帮助? 1.提高代码质量和可维护性:设计模式是经过验证的解决方案,有助于解决常见的设计问题。使用设计模式可以减少代码冗余,增强代码的可读性和可维护性,并提高代码的可靠性。 2.提升开发效率…...

英文阅读-LinkedIn‘s Tips for Highly Effective Code Review
LinkedIn的CR技巧 LinkedIn团队CodeReview经验与方法,原文来自https://thenewstack.io/linkedin-code-review/ 总结 Do I Understand the “Why”? 在提交pr的同时需要描述本次修改的“动机”,有助于提高代码文档质量。 Am I Giving Positive Feedbac…...
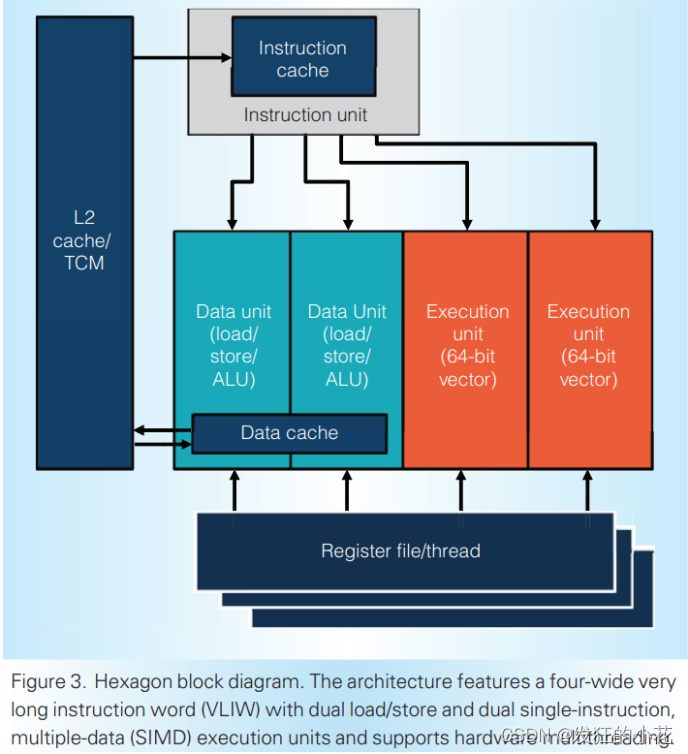
性能优化-高通的Hexagon DSP和NPU
原文来自【 Qualcomm’s Hexagon DSP, and now, NPU 】 本文主要介绍Qualcomm Hexagon DSP和NPU,这些为处理简单大量运算而设计的硬件。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
