在Windows虚拟机中挂载IP代理的流程
在虚拟机中挂载IP代理的步骤通常依赖于所使用的虚拟机软件(如VMware、VirtualBox等)以及代理服务器类型(HTTP/HTTPS/SOCKS)。以下是一个通用流程:
在Windows虚拟机中设置网络代理以使用代理IP:
1. SOCKS或HTTP(S)代理:
- 打开虚拟机内的网络设置,配置网络连接为“桥接模式”或者“NAT模式”,以便能够访问主机网络。
- 在虚拟机内部操作系统(例如Windows)上设置系统代理。对于Windows系统,可以通过以下步骤设置:
- 打开Internet选项(控制面板或设置中找到)。
- 转到“连接”标签页,点击“局域网设置”。
- 在“局域网(LAN)设置”窗口中,勾选“为LAN使用代理服务器”,并填写代理服务器的IP地址和端口。
2. 特定应用代理:
如果只需要某个应用程序通过代理,可以在该应用自身的网络设置里指定代理。
3. Linux虚拟机中使用Proxychains(如Kali Linux):
- 编辑`/etc/proxychains.conf`文件,添加代理服务器信息到`ProxyList`部分。
- 使用proxychains运行命令,这样所有通过proxychains启动的应用程序都会通过代理连接网络。
关于一个代理IP多台账号登录:
- 一般情况下,一个代理IP同时只能被一个客户端(账号)使用。
如果多个账号同时使用同一个代理IP登录,服务端可能会识别到这个情况,并可能根据其策略判断为异常行为,特别是在游戏或一些有严格用户协议的服务中,这可能导致账号被封禁。
- 对于需要多开账号并避免因IP重复而封号的情况,游戏工作室往往会采用不同的代理IP来分别登录每个账号,确保每个账号都有独立的IP地址。
- 高级的游戏防封代理IP服务可能会提供轮换IP的功能,但这仍然要求每个账号对应一个单独的IP连接通道,而不是共享一个IP。
相关文章:

在Windows虚拟机中挂载IP代理的流程
在虚拟机中挂载IP代理的步骤通常依赖于所使用的虚拟机软件(如VMware、VirtualBox等)以及代理服务器类型(HTTP/HTTPS/SOCKS)。以下是一个通用流程: 在Windows虚拟机中设置网络代理以使用代理IP: 1. SOCKS或H…...

软考之软件工程
一、瀑布模型 严格区分阶段,每个阶段因果关系紧密相连,只适合需求明确的项目 缺点:软件需求完整性、正确性难确定;严格串行化,很长时间才能看到结果;瀑布模型要求每个阶段一次性完全解决该阶段工作…...

微信小程序(六)tabBar的使用
注释很详细,直接上代码 上一篇 新增内容: 1. 标签栏文字的内容以及默认与选中颜色 2. 标签栏图标的默认样式与选中样式 3. 标签选项路径页面 4.标签栏背景颜色 🐼(文末补充)设置标签栏后为什么navigator标签无法跳转页…...

写Shell以交互方式变更Ubuntu的主机名
以下是一个简单的 Bash 脚本,用于以交互方式更改 Ubuntu 20 系统的主机名: 1#!/bin/bash 2 3# 提示用户输入新的主机名 4read -p "请输入新的系统名称(主机名): " new_hostname 5 6# 检查是否输入了新的主机名 7if [ -…...
SpringBoot整合ElasticSearch实现基础的CRUD操作
本文来说下SpringBoot整合ES实现CRUD操作 文章目录 概述spring-boot-starter-data-elasticsearch项目搭建ES简单的crud操作保存数据修改数据查看数据删除数据 本文小结 概述 SpringBoot支持两种技术和es交互。一种的jest,还有一种就是SpringData-ElasticSearch。根据…...
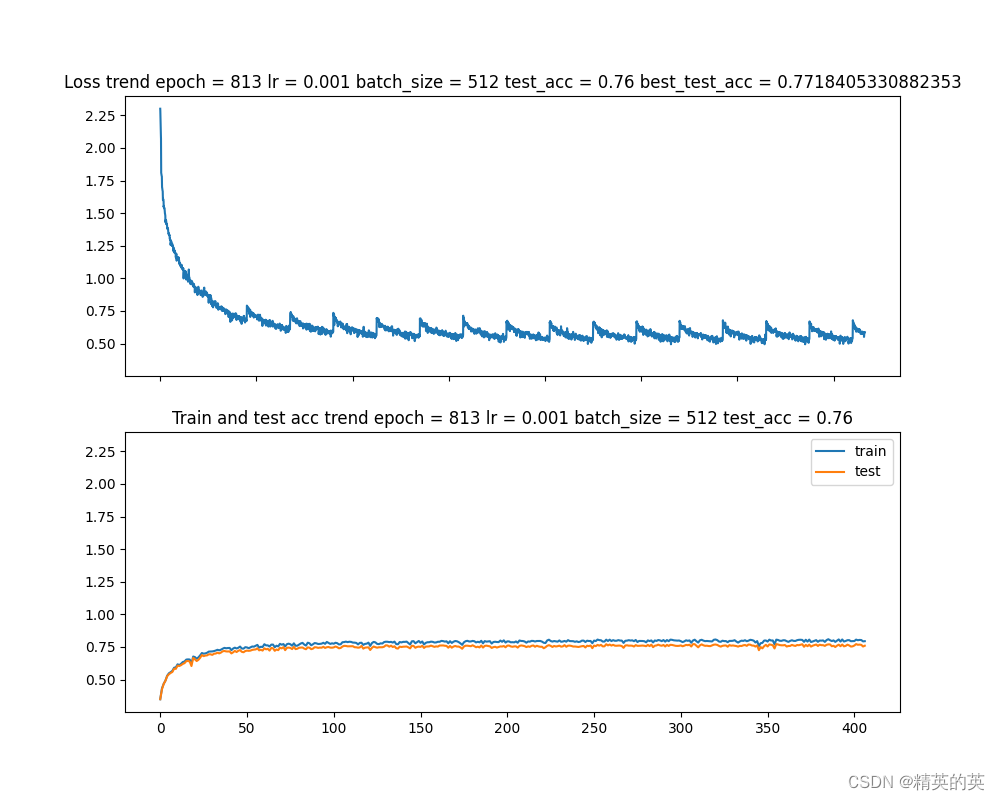
【PyTorch】记一次卷积神经网络优化过程
记一次卷积神经网络优化过程 前言 在深度学习的世界中,图像分类任务是一个经典的问题,它涉及到识别给定图像中的对象类别。CIFAR-10数据集是一个常用的基准数据集,包含了10个类别的60000张32x32彩色图像。在上一篇博客中,我们已…...

C++面试宝典第24题:袋鼠过河
题目 一只袋鼠要从河这边跳到河对岸,河很宽,但是河中间打了很多桩子。每隔一米就有一个桩子,每个桩子上都有一个弹簧,袋鼠跳到弹簧上就可以跳得更远。每个弹簧力量不同,用一个数字代表它的力量,如果弹簧力量为5,就代表袋鼠下一跳最多能够跳5米;如果为0,就会陷进去无法…...

2401vim,vim标号
标号简介 提供高亮,快速告诉用户有用信息.如,调试器在左侧列中有个表示断点的图标. 另一例可能是表示(PC)程序计数器的箭头.标号功能允许在窗口左侧放置标号或图标,并定义应用行的高亮. 此外,调试器还支持8到10种不同的标号和高亮颜色,见|NetBeans|. 使用标号有两个步骤: 1…...

Web开发中HTTP请求、响应等相关知识
目录 params和data区别? post请求可以使用params吗? put、delete请求应该使用params还是data? get和post的区别? 常用注解使用 params和data区别? 在使用Ajax时,"params" 和 "data" 通常用于不同的上下文。 "params…...

[Android] Android文件系统中存储的内容有哪些?
文章目录 前言root 文件系统/system 分区稳定性:安全性: /system/bin用来提供服务的二进制可执行文件:调试工具:UNIX 命令:调用 Dalvik 的脚本(upall script):/system/bin中封装的app_process脚本 厂商定制的二进制可执行文件: /system/xbin/system/lib[64]/system/…...
透明拼接屏在汽车领域的应用
随着科技的进步,透明拼接屏作为一种新型的显示技术,在汽车领域的应用越来越广泛。尼伽小编将围绕透明拼接屏在汽车本身、4S店、展会、工厂等方面的应用进行深入探讨,并展望未来的设计方向。 一、透明拼接屏在汽车本身的应用 车窗显示&#x…...

“深入理解RabbitMQ交换机的原理与应用“
深入理解RabbitMQ交换机的原理与应用 引言1. RabbitMQ交换机简介介绍1.1 什么是RabbitMQ?1.1.1 消息中间件的作用1.1.2 RabbitMQ的特点和优势 1.2 RabbitMQ的基本概念1.2.1 队列1.2.2 交换机1.2.3 路由键 1.3 交换机的作用和分类1.3.1 直连交换机(direct…...

Programming Abstractions in C阅读笔记:p248-p253
《Programming Abstractions in C》学习第69天,p248-p253总结,总计6页。 一、技术总结 “A generalized program for two-player games”如标题所示,该小节强调要学会从一个复杂的程序中抽象出通用的内容——这也是本书的主旨——“Program…...

面试题目,你对前端工程化的了解
前端工程化是通过工具和流程来提高软件开发效率、降低维护成本以及改善项目可维护性的方法。在前端领域,前端工程化通常包括以下方面内容 版本控制 使用 git 来管理代码的版本,追踪变更,协作开发等项目脚手架 使用项目的脚手架进行项目的初始…...

2023年春秋杯网络安全联赛冬季赛 Writeup
文章目录 Webezezez_phppicup Misc谁偷吃了外卖modules明文混淆 Pwnnmanagerbook Reupx2023 CryptoCF is Crypto Faker 挑战题勒索流量Ezdede 可信计算 Web ezezez_php 反序列化打redis主从复制RCE:https://www.cnblogs.com/xiaozi/p/13089906.html <?php c…...
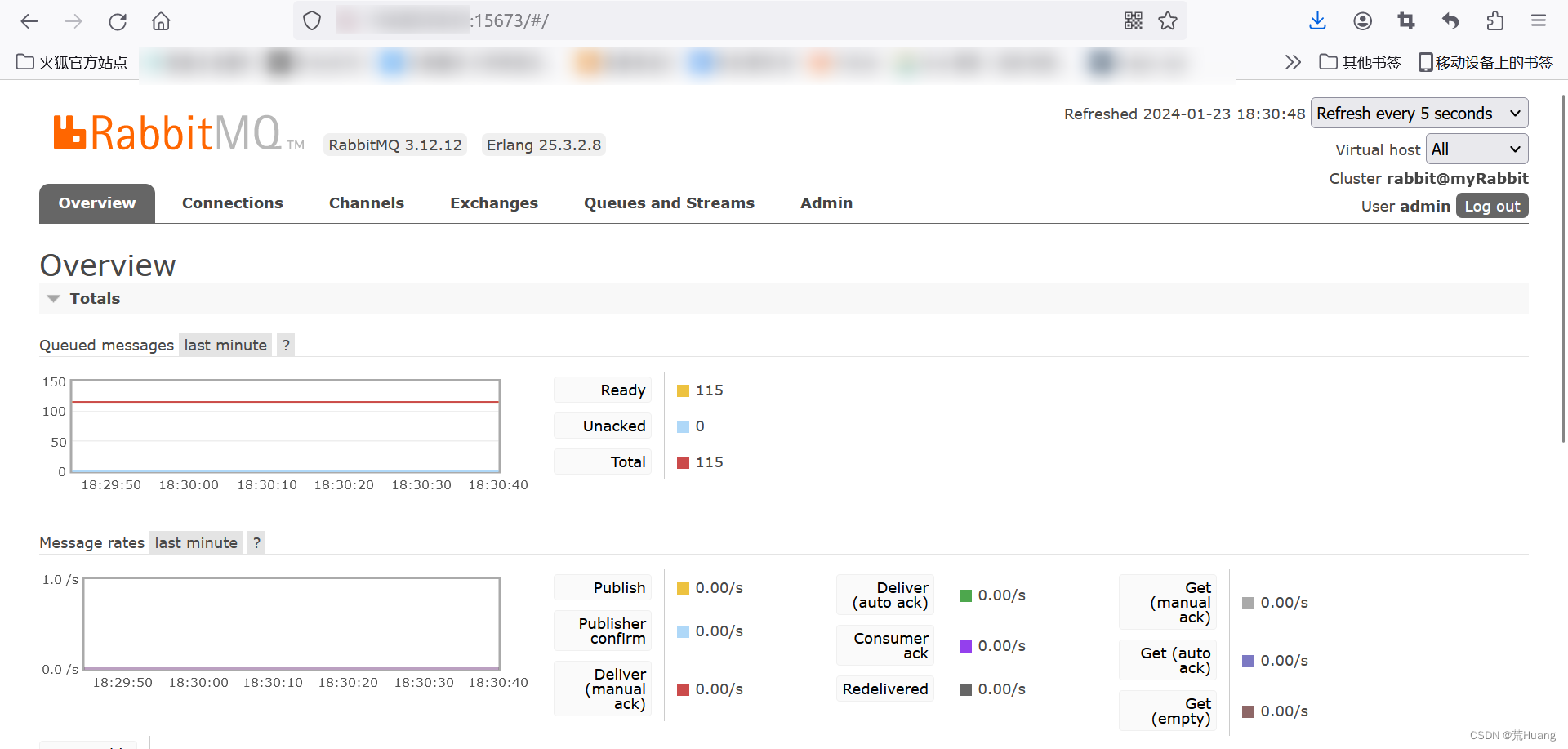
docker安装Rabbitmq教程(详细图文)
目录 1.下载Rabbitmq的镜像 2.创建并运行rabbitmq容器 3.启动web客户端 4.访问rabbitmq的微博客户端 5.遇到的问题 问题描述:在rabbitmq的web客户端发现界面会弹出如下提示框Stats in management UI are disabled on this node 解决方法 (1&#…...

java web mvc-05-JSF JavaServer Faces 入门例子
拓展阅读 Spring Web MVC-00-重学 mvc mvc-01-Model-View-Controller 概览 web mvc-03-JFinal web mvc-04-Apache Wicket web mvc-05-JSF JavaServer Faces web mvc-06-play framework intro web mvc-07-Vaadin web mvc-08-Grails 开源 The jdbc pool for java.(java …...

yolov8 训练voc数据集
yolov8训练 from ultralytics import YOLO# 加载模型 # model YOLO(yolov8n.yaml) # 从YAML构建新模型 # model YOLO(yolov8n.pt) # 加载预训练模型(推荐用于训练) model YOLO(yolov8n.yaml).load(yolov8n.pt) # 从YAML构建并转移权重# 训练模型…...

Python笔记12-多线程、网络编程、正则表达式
文章目录 多线程网络编程正则表达式 多线程 现代操作系统比如Mac OS X,UNIX,Linux,Windows等,都是支持“多任务”的操作系统。 进程: 就是一个程序,运行在系统之上,那么便称之这个程序为一个运…...

X射线中关于高频高压发生器、高清晰平板探测器、大热容量X射线球管、远程遥控系统的解释
高频高压发生器(High Frequency High Voltage Generator) 在医用诊断X射线设备中扮演着关键角色,它主要用于产生并控制用于X射线成像的高压电能。 这种发生器采用高频逆变技术,通过将输入的低电压、大电流转换为高电压、小电流&am…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
