信息检索与数据挖掘 | (九)Link Analysis(链接分析)
文章目录
- 📚链接分析
- 📚随机矩阵
- 📚random walk
- 📚Google formulation
📚链接分析
-
将链接看做投票,从重要的网站来的链接其权重更高,所以是递归定义的。
-
如果网页j权重为rj,有n个出边,每个出边的权重为rj/n,而网页j的自身权重为所有入边的权重之和。定义如下:

-
3个未知数3个方程没有唯一解,都是free的,所以可以引入限制sum=1

📚随机矩阵

- 使用矩阵表达,r=Mr:

- 该随机邻近矩阵M每列求和为1,对于向量r来说,列元素求和为1,ri表示i的重要性评分。同时r是M的特征向量,对应的特征值为1,由于1是M的最大特征值,所以可以使用幂迭代法对r进行快速求解:

📚random walk
-
t时刻,浏览者在网页i,在t+1时刻,从i的超链接中随机选择一个作为下一个浏览的网页,选择每一个网页的概率是一致的 p ( t + 1 ) = M ⋅ p ( t ) p(t+1)=M·p(t) p(t+1)=M⋅p(t)。
-
假设随机游走达到一个状态 p ( t + 1 ) = M ⋅ p ( t ) = p ( t ) p(t+1)=M·p(t)=p(t) p(t+1)=M⋅p(t)=p(t)时,称pt为随机游走的稳定分布。
-
我们的原始r向量满足r=Mr,所以r就是随机游走的稳定分布。
-
满足确定条件的图来说其稳定分布是存在且唯一的,且无论初始向量是什么最后一定会到达平稳分布
📚Google formulation
-
原来表达形式的问题:不一定会收敛,或者收敛不到我们想要的结果
-
可能存在的两种特殊情况:
-
dead end:没有出边,随机行走没有下一个点可以选择,容易造成泄漏
-
spider traps:环,所有的出边都在环内,将被困在环中,最终,spider trap吸收了所有的importance
-
-
举例:如果走到m,则不会跳出,将一直访问m,最后r向量收敛为[0,0,1]。

-
解决方法:随机跳转teleports
- 在每一个时间t中,用户有两种选择,以概率beta随机选择一个连接进行随即游走,或者以概率 1 − β 1-\beta 1−β进行随机跳转, β \beta β一般在0.8-0.9之间。进而用户可以跳出spider trap。
- 同时对于dead-ends来说用户直接执行随机跳转,此时访问其他连接的概率为1/N。
-
理解
-
spider-traps不是问题,但是trap的pagerank 评分不是我们想要的,所以我们使用随机跳转在有限步内跳出trap,不会被困在里面
-
dead-ends是一个问题,因为此时列向量不是随机向量,不满足初始条件,所以我们在之上执行随机游走,将列向量变为随机向量
-
最后公式变为:

-
此时矩阵A可以写为:

-
从而 r = A ⋅ r r=A·r r=A⋅r,依然可以使用幂迭代法,实际中 β \beta β=0.8
-

-
- 补充博客:pagerank算法实现
- PageRank算法中Power Iteration的解释。
- Power Iteration的基本思想是通过不断迭代更新网页的权重值,直到收敛。
- 以下是Power Iteration算法的基本步骤:
- 初始化:将所有网页的初始PageRank值设置为相同的数值,通常为1/N,其中N是网页的总数。
- 迭代计算:重复进行以下步骤,直到收敛为止:
- 对于每个网页i,根据其当前的PageRank值和其出链的数量来计算对其他网页的贡献值(即将自己的PageRank值平均分配给其出链的网页)。
- 将网页i的贡献值累加到其每个入链网页j的PageRank值上。
- 对每个网页j,根据收到的所有入链网页的贡献值来更新其新的PageRank值。
- 收敛判定:当所有网页的PageRank值变化小于设定的阈值时,算法收敛。
- Power Iteration的核心思想是通过不断传递和累积网页权重值,直到每个网页的PageRank值稳定下来。
相关文章:

信息检索与数据挖掘 | (九)Link Analysis(链接分析)
文章目录 📚链接分析📚随机矩阵📚random walk📚Google formulation 📚链接分析 将链接看做投票,从重要的网站来的链接其权重更高,所以是递归定义的。 如果网页j权重为rj,有n个出边&…...

yarn的安装及使用教程
Yarn 是一个快速、可靠、安全的包管理工具,用于管理 JavaScript 项目的依赖项。下面是关于 Yarn 的安装和基本使用的详细教程: 安装 Yarn 访问 Yarn 官网 并按照指示下载适合你操作系统的安装程序。安装程序会自动安装 Yarn,并将其添加到系…...

最新AI系统ChatGPT网站H5系统源码,支持Midjourney绘画,GPT语音对话+ChatFile文档对话总结+DALL-E3文生图
一、前言 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧。已支持GPT…...

学会使用ubuntu——ubuntu22.04使用WebCatlog
Ubuntu22.04使用WebCatlog WebCatlog是适用于Gnu / Linux,Windows或Mac OS X系统的桌面程序。 引擎基于铬,它用于在我们的桌面上处理Web服务。简单点就是把网页单独一个窗口出来显示,当一个app用。本文就是利用WebCatlog安装后的notion编写的…...
Python3.8批量裁剪利用shp文件裁剪tif栅格影像数据)
(Arcgis)Python3.8批量裁剪利用shp文件裁剪tif栅格影像数据
使用环境: pycharm2020 arcgis pro 中的python3.8 一、pycharm中设置python编译器。左上角“文件”——“设置”——找到python interpreter——找到arcgis pro安装文件夹中的python D:\ArcGIS Pro\bin\Python\envs\arcgispro-py3\python.exe使用arcgis pro原因&a…...

漏洞补丁修复之openssl版本从1.1.1q升级到1.1.1t以及python版本默认2.7.5升级到2.7.18新版本和Nginx版本升级到1.24.0
一、Openssl升级 1、查看Openssl安装的版本 openssl version 2、查看Openssl路径 which openssl 3、上传openssl安装包到服务器:openssl-1.1.1t.tar.gz,并且解压,安装: mv /usr/local/openssl /usr/local/backup_openssl_1.1.1q_20240120 mkdir /usr/local/openssl tar…...
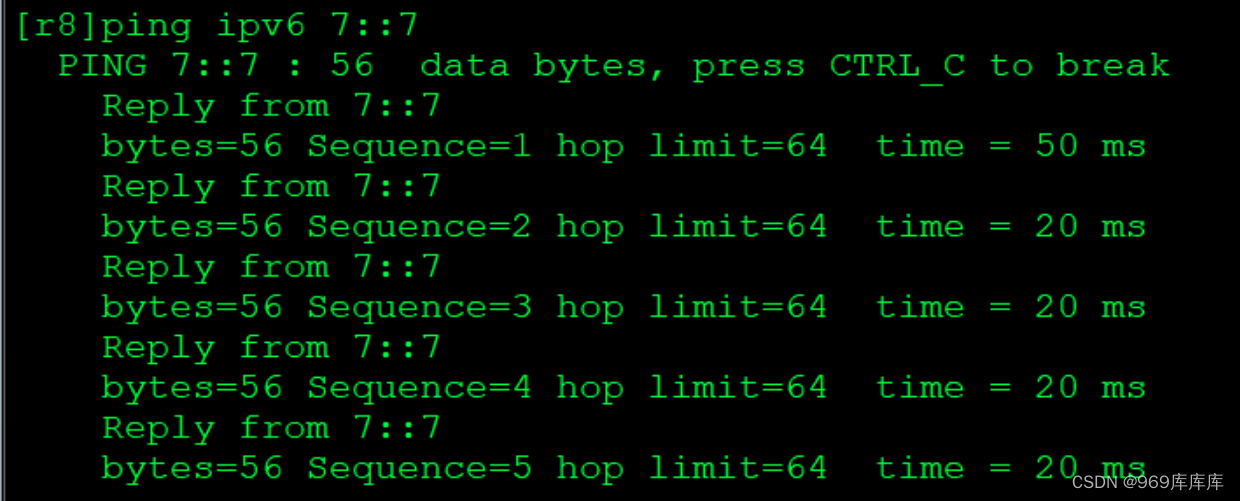
HCIP-BGP实验4
搭建实验拓扑图 要求 1.全网可达 2.isp只能配置IP地址 实验开始 配置IP地址及环回 r1,r2,r9,r10配ipv4地址(以r1为例) [Huawei]sysname r1 [r1]interface g0/0/0 [r1-GigabitEthernet0/0/0]ip address 12.1.1.1 24 [r1-GigabitEthernet0/0/0]q [r1]interface LoopBack 0…...

数据挖掘笔记1
课程:清华大学-数据挖掘:理论与算法(国家级精品课)_哔哩哔哩_bilibili 一、Learning Resources 二、Data 数据是最底层的一种表现形式。数据具有连续性。从存储上来讲,数据分为逻辑上的和物理层的。大数据࿱…...

Spring RabbitMQ那些事(3-消息可靠传输和订阅)
目录 一、序言二、生产者确保消息发送成功1、为什么需要Publisher Confirms2、哪些消息会被确认处理成功 三、消费者保证消息被处理四、Spring RabbitMQ支持代码示例1、 application.yml2、RabbigtMQ配置3、可靠生产者配置4、可靠消费者配置5、测试用例 一、序言 在有些业务场…...

揭秘 Kafka 高性能之谜:一文读懂背后的设计精粹与技术实现
Kafka在性能方面有着显著的优势,这也使得Kafka的应用非常广泛,那kakfa的性能为何如此优异呢?本文将带你探寻kafka高性能之谜。 kafka的高性能概括起来有如下几点:顺序写入磁盘与I/O优化、批量处理、页缓存、零拷贝技术、分区并行处…...

canvas绘制美国国旗(USA Flag)
查看专栏目录 canvas实例应用100专栏,提供canvas的基础知识,高级动画,相关应用扩展等信息。canvas作为html的一部分,是图像图标地图可视化的一个重要的基础,学好了canvas,在其他的一些应用上将会起到非常重…...

Python中的`__all__`魔法函数使用详解
概要 Python是一门灵活而强大的编程语言,提供了各种机制来控制模块的导入和访问。其中,__all__魔法函数是一种用于限制模块导入的机制,可以明确指定哪些变量、函数或类可以被导入。本文将深入探讨__all__的作用、用法以及示例,以…...

Studio One 6 mac 6.5.2 激活版 数字音乐编曲创作
PreSonus Studio One是PreSonus出品的一款功能强大的音乐创作软件。主要为用户提供音乐创作、录音、编辑、制作等功能。它可以让你创造音乐,无限的轨道,无限的MIDI和乐器轨道,虚拟乐器和效果通道,这些都是强大和完美的。 软件下载…...

GitHub图床TyporaPicGo相关配置
本文作者: slience_me 文章目录 GitHub图床&Typora&PicGo相关配置1. Github配置2. picGo配置3. Typora配置 GitHub图床&Typora&PicGo相关配置 关于Typora旧版的百度网盘下载路径 链接:https://pan.baidu.com/s/12mq-dMqWnRRoreGo4MTbKg?…...

FireAlpaca:轻量级、免费的Mac/Win绘图软件,让你的创意如火燃烧!
FireAlpaca是一款轻量级、免费的绘图软件,适用于Mac和Win系统,让你的创作过程更加快捷、简便。无论是绘制漫画、插图、设计作品还是进行简单的图片编辑,FireAlpaca都能满足你的需求。 首先,FireAlpaca具有直观友好的用户界面&…...

用 Python 制作可视化 GUI 界面,一键实现自动分类管理文件!
经常杂乱无章的文件夹会让我们找不到所想要的文件,因此小编特意制作了一个可视化GUI界面,通过输入路径一键点击实现文件分门别类的归档。 不同的文件后缀归类为不同的类别 我们先罗列一下大致有几类文件,根据文件的后缀来设定,大…...
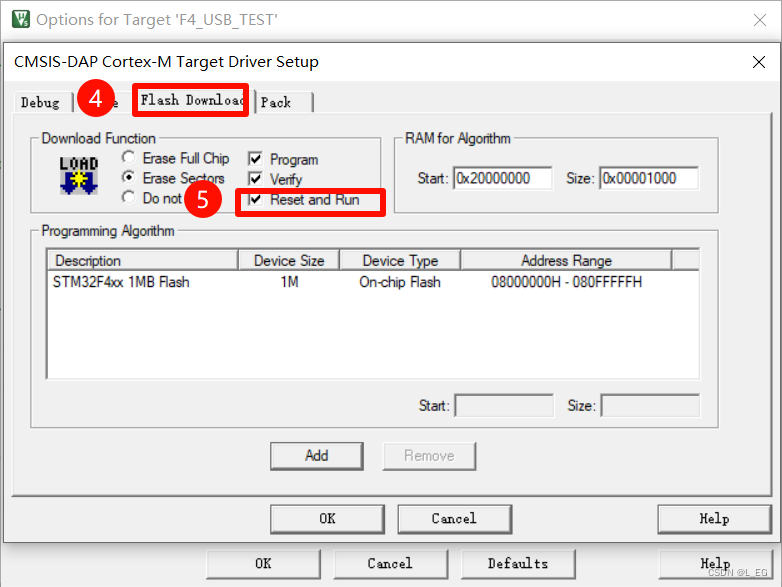
【STM32】USB程序烧录需要重新上电 软件复位方法
文章目录 一、问题二、解决思路2.1 直接插拔USB2.2 给芯片复位 三、解决方法3.1 别人的解决方法3.2 在下载界面进行设置 一、问题 最近学习STM32的USB功能,主要是想要使用虚拟串口功能(VCP),发现每次烧录之后都需要重新上电才可以…...
)
Java数据结构与算法:图算法之深度优先搜索(DFS)
Java数据结构与算法:图算法之深度优先搜索(DFS) 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,一个热爱编程的程序猿。今天,让我们一起探索图算法中的深度优先搜索(DFS&…...
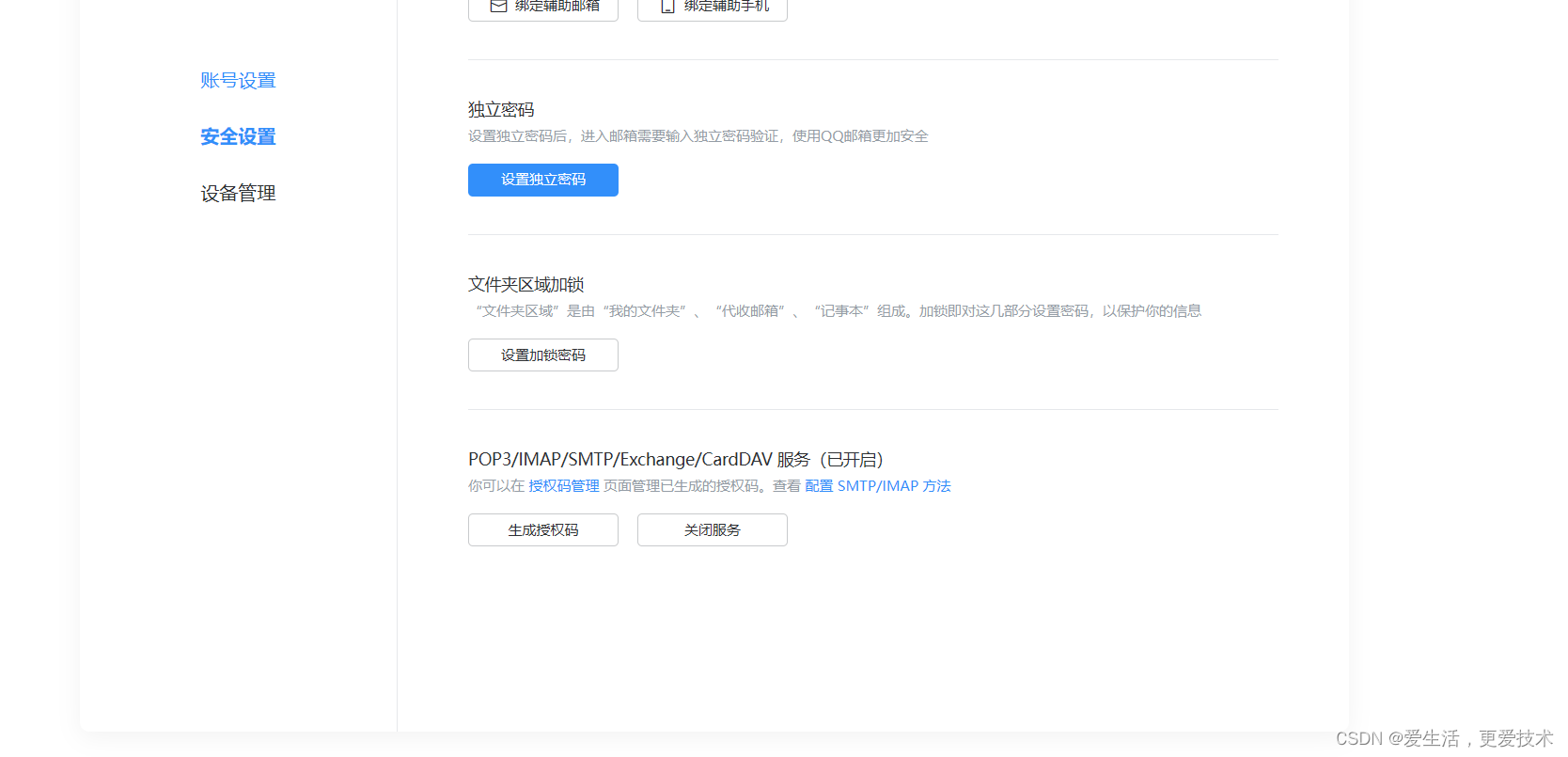
SpringBoot整合QQ邮箱发送验证码
一、QQ开启SMTP 打开QQ邮箱,点击设置,进入账号,往下滑后,看见服务状态后,点击管理服务 进入管理服务后,打开服务,然后获取授权码 二 、导入依赖 <!-- 邮箱--><dependency>&…...
云虚拟主机怎么修改代码?如何修改部署在虚拟主机的网站代码?
很多站长成功创建网站之后,或多或少都会对网站代码进行适当修改。比如boke112百科使用YIA主题后,也根据自己的需要进行了多个方面的小修改。 那么如果网站是部署在虚拟主机上的,那么应该如何修改这些网站代码呢?其实,…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
