代码随想录算法训练营第十四天|● 理论基础 ● 递归遍历 ● 迭代遍历 ● 统一迭代
仅做学习笔记,详细请访问代码随想录
● 理论基础
● 递归遍历
● 迭代遍历
● 统一迭代
单层递归的逻辑就是按照中左右的顺序来处理的,这样二叉树的前序遍历,基本就写完了,再看一下完整代码:
前序遍历:
class Solution {
public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;vec.push_back(cur->val); // 中traversal(cur->left, vec); // 左traversal(cur->right, vec); // 右}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};那么前序遍历写出来之后,中序和后序遍历就不难理解了,代码如下:
中序遍历:
void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec); // 左vec.push_back(cur->val); // 中traversal(cur->right, vec); // 右
}后序遍历:
void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec); // 左traversal(cur->right, vec); // 右vec.push_back(cur->val); // 中
}● 迭代遍历
前序遍历(迭代法)
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top(); // 中st.pop();result.push_back(node->val);if (node->right) st.push(node->right); // 右(空节点不入栈)if (node->left) st.push(node->left); // 左(空节点不入栈)}return result;}
};
中序遍历(迭代法)
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点,访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left; // 左} else {cur = st.top(); // 从栈里弹出的数据,就是要处理的数据(放进result数组里的数据)st.pop();result.push_back(cur->val); // 中cur = cur->right; // 右}}return result;}
};
后序遍历(迭代法)
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->left) st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)if (node->right) st.push(node->right); // 空节点不入栈}reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了return result;}
};
● 统一迭代
迭代法中序遍历
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中if (node->right) st.push(node->right); // 添加右节点(空节点不入栈)st.push(node); // 添加中节点st.push(NULL); // 中节点访问过,但是还没有处理,加入空节点做为标记。if (node->left) st.push(node->left); // 添加左节点(空节点不入栈)} else { // 只有遇到空节点的时候,才将下一个节点放进结果集st.pop(); // 将空节点弹出node = st.top(); // 重新取出栈中元素st.pop();result.push_back(node->val); // 加入到结果集}}return result;}
};
迭代法前序遍历
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();if (node->right) st.push(node->right); // 右if (node->left) st.push(node->left); // 左st.push(node); // 中st.push(NULL);} else {st.pop();node = st.top();st.pop();result.push_back(node->val);}}return result;}
};
迭代法后序遍历
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();st.push(node); // 中st.push(NULL);if (node->right) st.push(node->right); // 右if (node->left) st.push(node->left); // 左} else {st.pop();node = st.top();st.pop();result.push_back(node->val);}}return result;}
};
相关文章:

代码随想录算法训练营第十四天|● 理论基础 ● 递归遍历 ● 迭代遍历 ● 统一迭代
仅做学习笔记,详细请访问代码随想录 ● 理论基础 ● 递归遍历 ● 迭代遍历 ● 统一迭代 单层递归的逻辑就是按照中左右的顺序来处理的,这样二叉树的前序遍历,基本就写完了,再看一下完整代码: 前序遍历: …...

❤css实用
❤ css实用 渐变色边框(Gradient borders方法的汇总 5种) 给 border 设置渐变色是很常见的效果,实现这个效果有很多思路 1、使用 border-image 使用 css 的 border-image 属性给 border 绘制复杂图样 与 background-image 类似,我…...
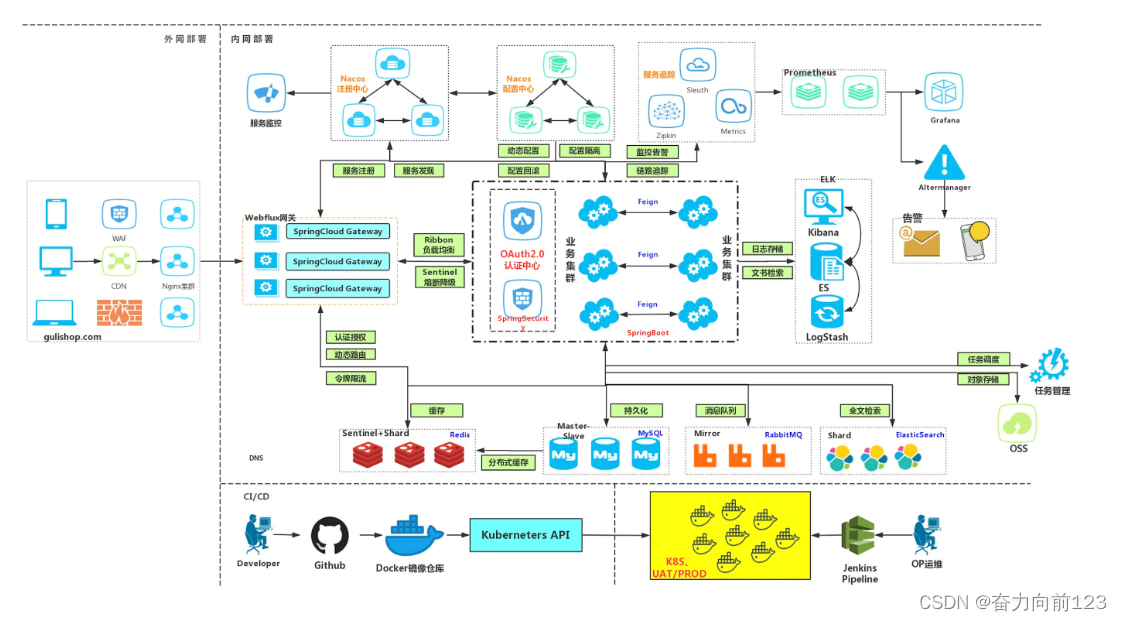
web系统架构基于springCloud的各技术栈
博主目前开发的web系统架构是基于springCloud的一套微服务架构。 使用的技术栈:springbootmysqlclickhousepostgresqlredisrocketMqosseurekabase-gatewayapollodockernginxvue的一套web架构。 一、springboot3.0 特性:Spring Boot 3.0提供了许多新特性…...
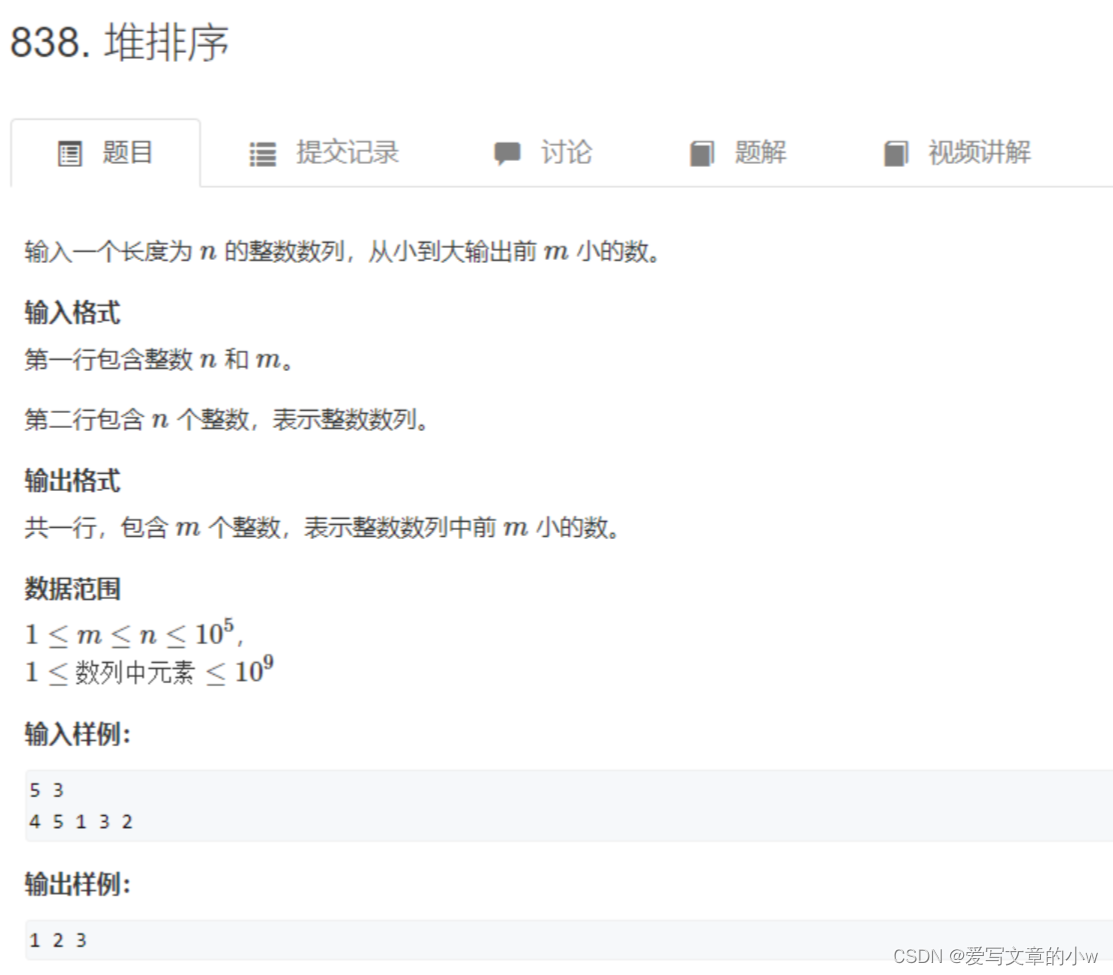
【第十五课】数据结构:堆 (“堆”的介绍+主要操作 / acwing-838堆排序 / 时间复杂度的分析 / c++代码 )
目录 关于堆的一些知识的回顾 数据结构:堆的特点 "down" 和 "up":维护堆的性质 down up 数据结构:堆的主要操作 acwing-838堆排序 代码如下 时间复杂度分析 确实是在写的过程中频繁回顾了很多关于树的知识&…...

el-select选项过多导致页面卡顿,路由跳转卡顿
问题:el-select数据量太大,导致渲染过慢,或造成页面卡顿甚至于卡死 卡顿原因:DOM中数据过多,超过内存限制 解决方法: 1.使用Virtualized Select 虚拟化选择器,页面就不卡了 2.el-select做分…...

信息流广告参数回传工具怎么做联调
信息流广告在抖音等平台上越来越受到广告主的青睐,它能够在用户浏览内容的同时,以自然的方式展示广告,提高曝光率和点击率。然而,为了更好地评估广告效果,需要进行参数回传联调。本文将介绍一种实用的工具——数灵通外…...

matlab appdesigner系列-常用18-表格
表格,常用来导入外部表格数据 示例: 导入外界excel数据:data.xlsx 姓名年龄城市王一18长沙王二21上海王三56武汉王四47北京王五88成都王六23长春 操作步骤如下: 1)将表格拖拽到画布上 2)对app1右键进行…...
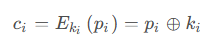
密码学的100个基本概念
密码学作为信息安全的基础,极为重要,本文分为上下两部分,总计10个章节,回顾了密码学的100个基本概念,供小伙伴们学习参考。本文将先介绍前五个章节的内容。 一、密码学历史 二、密码学基础 三、分组密码 四、序列密码 五、哈希…...

Python中的进制转换——bin/oct/hex函数与int函数
简介 进制转换可能是一个工作学习中的常见小任务,手写相关函数显然很麻烦。 Python有相关内置函数一般能满足我们的需求。bin()、oct()、hex()将十进制转换为常用的二、八、十六进制,而 int()函数可指定第二个参数从而将其它进制转换为十进制。或许后者…...
RT-Thread 瑞萨 智能家居网络开发:RA6M3 HMI Board 以太网+GUI技术实践
不用放大了, 我在包里找到张不小的…… 以太网HMI线下培训-环境准备 这是社群的文档:【腾讯文档】以太网线下培训(HMI-Board) https://docs.qq.com/doc/DY0FIWFVuTEpORlNn 先介绍周六的培训是啥,然后再介绍一下要准…...

力扣刷题第十天 美丽塔 一
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。 你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。 如果以下条件满足,我们称这些塔是 美丽 的: 1 < heights[i] < maxHeights[i]heights 是一个 山脉…...

c# ADODB.Recordset实例调用Fields报错
代码: using System; using System.CodeDom; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using ADODB;namespace ConsoleApp1 {internal class Programre{static ADODB.Recordset recordsetInstance…...
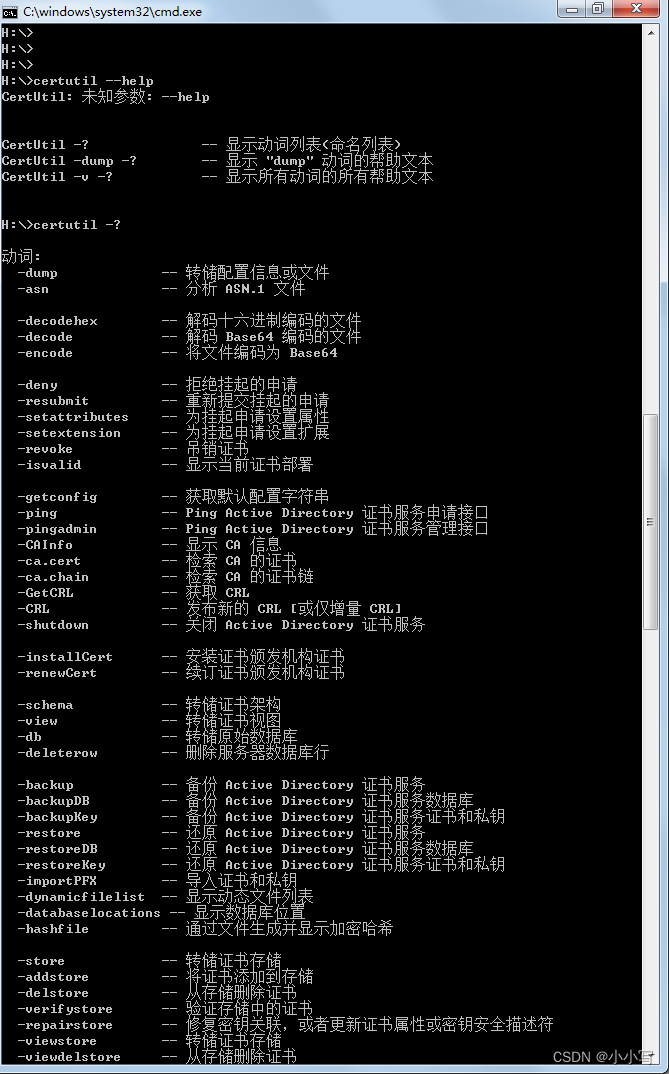
windows和linux下SHA1,MD5,SHA256校验办法
今天更新android studio到Android Studio Hedgehog | 2023.1.1时,发现提示本机安装的git版本太老,于是从git官网下载最新的git。 git下载地址: https://git-scm.com/ 从官网点击下载最新windows版本会跳转到github仓库来下载发布的git&…...

高新技术企业申报需要具备哪些条件?
(一)企业申请认定时须注册成立一年以上; (二)企业通过自主研发、受让、受赠、并购等方式,获得对其主要产品(服务)在技术上发挥核心支持作用的知识产权的所有权; &#…...

测试不拘一格——掌握Pytest插件pytest-random-order
在测试领域,测试用例的执行顺序往往是一个重要的考虑因素。Pytest插件 pytest-random-order 提供了一种有趣且灵活的方式,让你的测试用例能够以随机顺序执行。本文将深入介绍 pytest-random-order 插件的基本用法和实际案例,助你摆脱固定的测试顺序,让测试更具变化和全面性…...
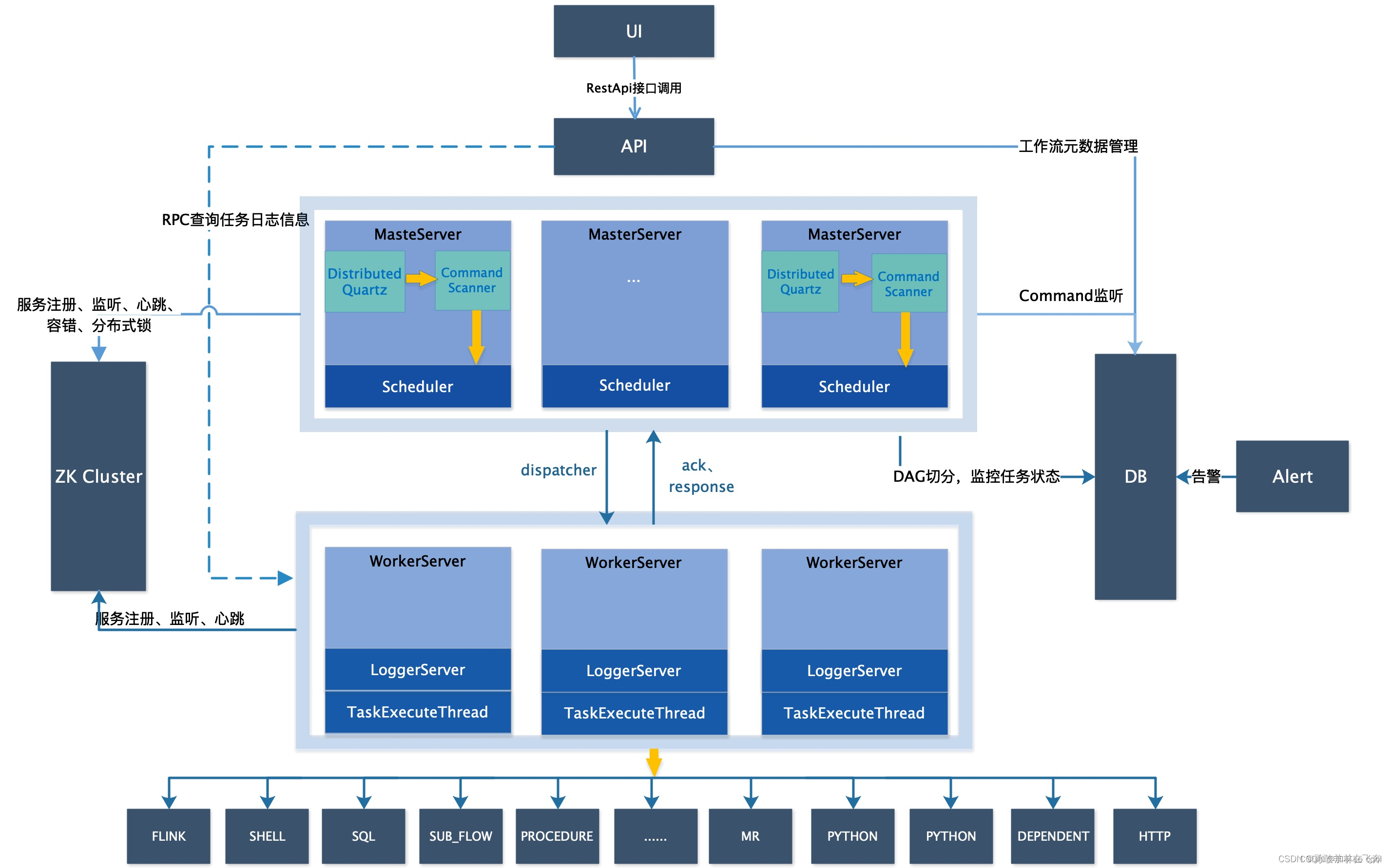
DophineScheduler通俗版
1.DophineScheduler的架构 ZooKeeper: AlertServer: UI: ApiServer: 一个租户下可以有多个用户;一个用户可以有多个项目一个项目可以有多个工作流定义,每个工作流定义只属于一个项目;一个租户可…...

企业如何稳步开启SASE实施之路
在上一篇题为《企业为什么选择SASE?香港电讯专家给你答案!》的文章中,我们从SD-WAN的安全策略和能力、市场趋势的推动及SASE的四大特性分析了企业选择采用安全访问服务边缘(SASE)的原因。基于SASE的各项优势࿰…...
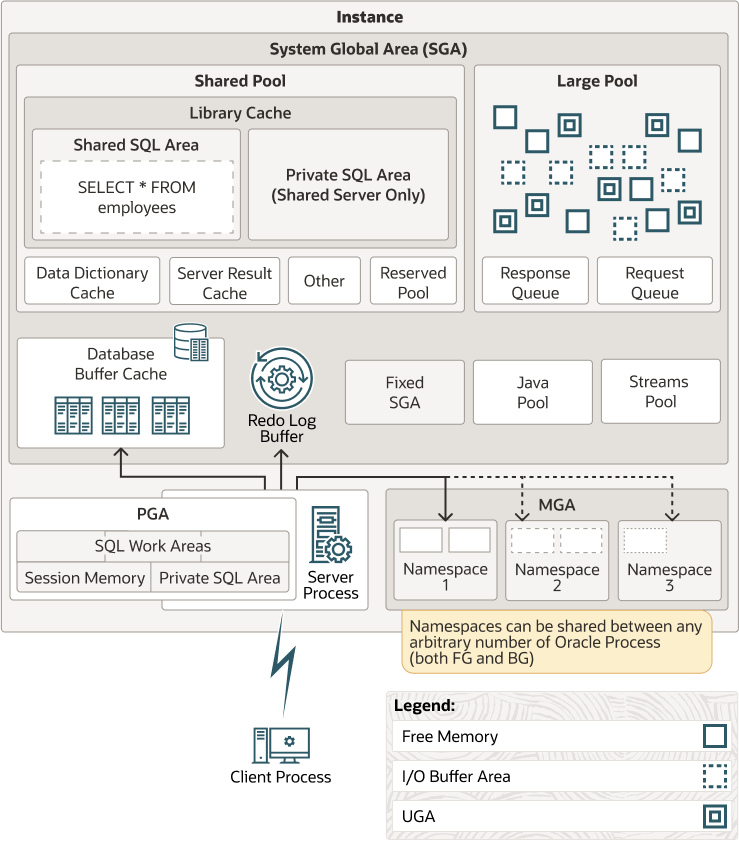
【Oracle】收集Oracle数据库内存相关的信息
文章目录 【Oracle】收集Oracle数据库内存相关的信息收集Oracle数据库内存命令例各命令的解释输出结果例参考 【声明】文章仅供学习交流,观点代表个人,与任何公司无关。 编辑|SQL和数据库技术(ID:SQLplusDB) 【Oracle】收集Oracle数据库内存相关的信息 …...

MySQL也开始支持JavaScript了
2023 年 12 月 16 日,Oracle 公司在一篇名为 《Introducing JavaScript support in MySQL》的文章中宣布 MySQL 数据库服务器将开始支持 JavaScript 语言。 这个举措标志着继PostgreSQL之后, MySQL 也支持使用 JavaScript 编写函数和存储过程了。作为最…...

百度大脑 使用
百度大脑: 官方网址:https://ai.baidu.com/ 文档中心:https://ai.baidu.com/ai-doc 体验中心:https://ai.baidu.com/experience 百度大脑则是百度AI核心技术引擎,它包括基础层、感知层、认知层和安全,是百…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
