【MIdjourney】一些材质相关的关键词
1.多维剪纸(Multidimensional papercut)
"Multidimensional papercut"(多维剪纸)是一种剪纸艺术形式,通过多层次的剪纸技巧和设计来创造出立体感和深度感。这种艺术形式通常涉及在不同的纸层上剪裁不同的图案,并将它们叠加在一起,以形成一个立体的、多维的作品。
这种剪纸艺术形式有时被用于创作立体的贺卡、装饰品、艺术品等,展示了艺术家对纸质材料和空间感的独特处理技巧。Multidimensional papercut常常展示了艺术家的技艺和创造力,同时为观众提供了一种沉浸式的视觉体验。
2.微缩模型(Miniature)
"Miniature"(微缩模型)通常指的是小型的、比实际物体或场景更小的模型或艺术品。这可以涵盖各种领域,包括艺术、手工艺、建筑、模型制作等。Miniature通常用于展示精细的工艺和详细的设计。
例如大家小时候玩的绿色小人。
3.羊毛毡(Wool Felt,fox)
"Wool Felt"(羊毛毡)是一种由羊毛纤维制成的织物。它通常是通过将羊毛纤维压缩在一起,然后通过湿热和压缩的处理而形成的。这种过程使得羊毛纤维之间的毛羽交错,形成了一个坚固而致密的织物。
羊毛毡广泛用于制作各种产品,包括衣物、帽子、手套、靴子、家居装饰品等。由于其天然的特性和良好的手感,羊毛毡在手工艺品、纺织品和设计领域中也很受欢迎。
4.立体像素风(Voxel)
"Voxel"是三维图形学中的一个术语,它是三维空间中的体素(Volumetric Pixel)的简称。体素是空间中的三维像素,类似于二维图像中的像素。每个体素表示三维空间中的一个体积元素,具有位置、颜色和其他属性。
既有点像乐高(LEGO),又有点像我的世界(Minecraft),生成图片的时候可以添加这两个关键词。
5.雕刻建模(Claymorphism)
ZBrush是一款专业的数字雕刻和3D建模软件,由Pixologic公司开发。它在数字艺术、游戏开发、影视特效等领域广泛应用,以其强大的雕刻和绘画工具而闻名。
相关文章:

【MIdjourney】一些材质相关的关键词
1.多维剪纸(Multidimensional papercut) "Multidimensional papercut"(多维剪纸)是一种剪纸艺术形式,通过多层次的剪纸技巧和设计来创造出立体感和深度感。这种艺术形式通常涉及在不同的纸层上剪裁不同的图案,并将它们…...

递归组件怎么实现无线滚动
递归组件实现无限滚动的方法通常涉及到对数据的递归处理和组件的自我调用。以下是一个简单的示例,展示如何使用递归组件实现无限滚动: 首先,定义一个递归组件,该组件可以调用自己来渲染下一组数据。假设我们要展示一个滚动列表&a…...

致远OA如何开发 第十篇 数据库
数据库 此栏目技术支持 技术大佬对栏目文章的支持 特别感谢 如何编写dao实现数据的增删改查 新建文件 实现下面的方法即可,具体的sql操作需要自己组装 其中JDBCAgent 是致远封装过的工具Overridepublic void addData(String dataId, String agentId) {try (JDBC…...

信息检索与数据挖掘 | (十)线性回归与逻辑回归
文章目录 📚线性回归算法流程📚Bias and variance📚过拟合&欠拟合📚逻辑回归算法流程 📚线性回归算法流程 ybwx 使用loss function L来评估函数的好坏 从而我们要选择使L最小的模型参数w,b 使用梯度下降的方法…...

【issue-halcon例程学习】measure_arc.hdev
例程功能 检查倒角后铸件的细长孔之间的距离。 代码如下 read_image (Zeiss1, zeiss1) get_image_size (Zeiss1, Width, Height) dev_close_window () dev_open_window (0, 0, Width / 2, Height / 2, black, WindowHandle) set_display_font (WindowHandle, 14, mono, true,…...
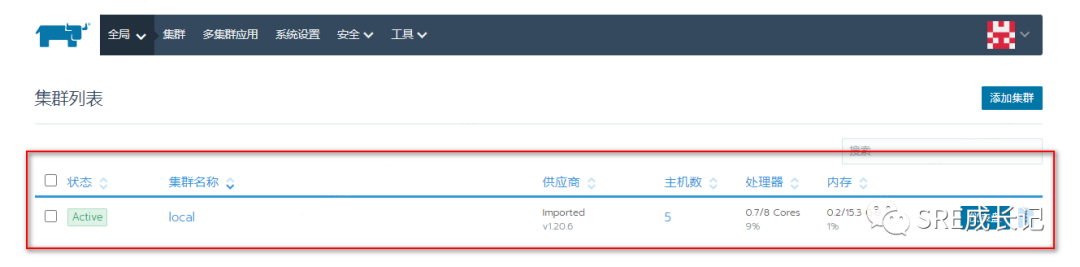
RKE快速搭建离线k8s集群并用rancher管理界面
转载说明:如果您喜欢这篇文章并打算转载它,请私信作者取得授权。感谢您喜爱本文,请文明转载,谢谢。 本文记录使用RKE快速搭建一套k8s集群过程,使用的rancher老版本2.5.7(当前最新版为2.7)。适用…...

代码随想录算法训练营第十四天|● 理论基础 ● 递归遍历 ● 迭代遍历 ● 统一迭代
仅做学习笔记,详细请访问代码随想录 ● 理论基础 ● 递归遍历 ● 迭代遍历 ● 统一迭代 单层递归的逻辑就是按照中左右的顺序来处理的,这样二叉树的前序遍历,基本就写完了,再看一下完整代码: 前序遍历: …...

❤css实用
❤ css实用 渐变色边框(Gradient borders方法的汇总 5种) 给 border 设置渐变色是很常见的效果,实现这个效果有很多思路 1、使用 border-image 使用 css 的 border-image 属性给 border 绘制复杂图样 与 background-image 类似,我…...
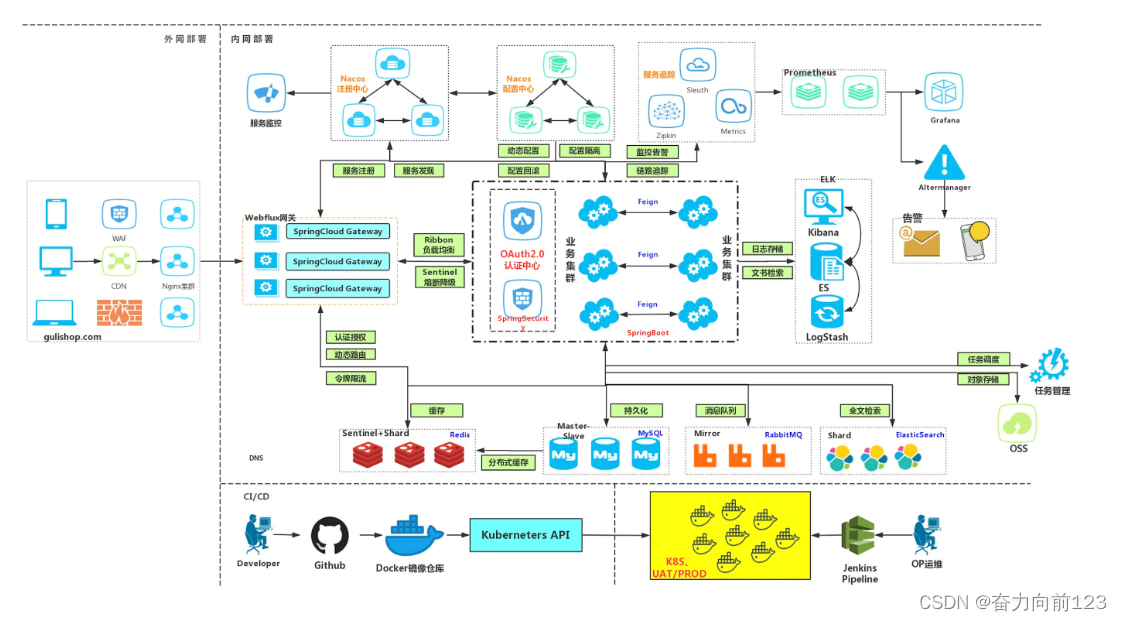
web系统架构基于springCloud的各技术栈
博主目前开发的web系统架构是基于springCloud的一套微服务架构。 使用的技术栈:springbootmysqlclickhousepostgresqlredisrocketMqosseurekabase-gatewayapollodockernginxvue的一套web架构。 一、springboot3.0 特性:Spring Boot 3.0提供了许多新特性…...
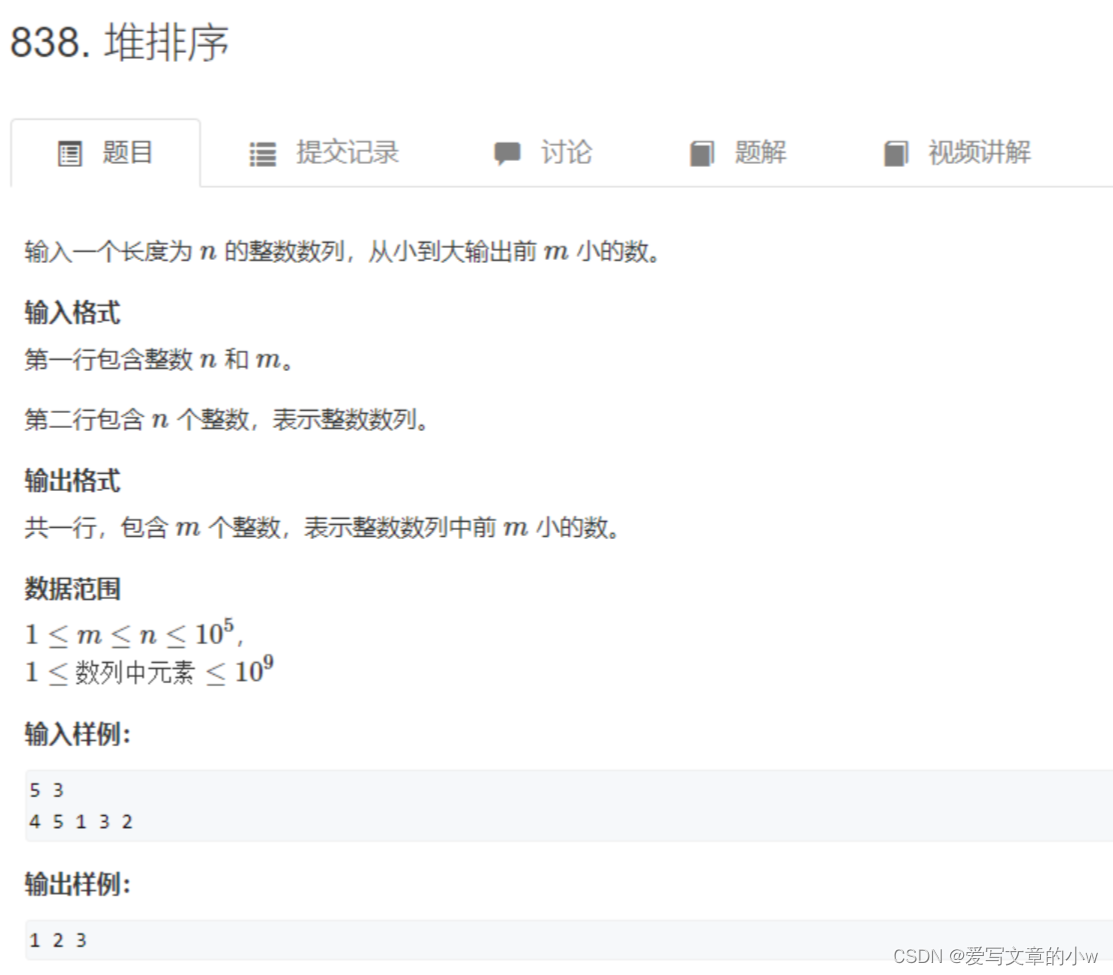
【第十五课】数据结构:堆 (“堆”的介绍+主要操作 / acwing-838堆排序 / 时间复杂度的分析 / c++代码 )
目录 关于堆的一些知识的回顾 数据结构:堆的特点 "down" 和 "up":维护堆的性质 down up 数据结构:堆的主要操作 acwing-838堆排序 代码如下 时间复杂度分析 确实是在写的过程中频繁回顾了很多关于树的知识&…...

el-select选项过多导致页面卡顿,路由跳转卡顿
问题:el-select数据量太大,导致渲染过慢,或造成页面卡顿甚至于卡死 卡顿原因:DOM中数据过多,超过内存限制 解决方法: 1.使用Virtualized Select 虚拟化选择器,页面就不卡了 2.el-select做分…...

信息流广告参数回传工具怎么做联调
信息流广告在抖音等平台上越来越受到广告主的青睐,它能够在用户浏览内容的同时,以自然的方式展示广告,提高曝光率和点击率。然而,为了更好地评估广告效果,需要进行参数回传联调。本文将介绍一种实用的工具——数灵通外…...

matlab appdesigner系列-常用18-表格
表格,常用来导入外部表格数据 示例: 导入外界excel数据:data.xlsx 姓名年龄城市王一18长沙王二21上海王三56武汉王四47北京王五88成都王六23长春 操作步骤如下: 1)将表格拖拽到画布上 2)对app1右键进行…...
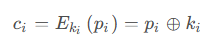
密码学的100个基本概念
密码学作为信息安全的基础,极为重要,本文分为上下两部分,总计10个章节,回顾了密码学的100个基本概念,供小伙伴们学习参考。本文将先介绍前五个章节的内容。 一、密码学历史 二、密码学基础 三、分组密码 四、序列密码 五、哈希…...

Python中的进制转换——bin/oct/hex函数与int函数
简介 进制转换可能是一个工作学习中的常见小任务,手写相关函数显然很麻烦。 Python有相关内置函数一般能满足我们的需求。bin()、oct()、hex()将十进制转换为常用的二、八、十六进制,而 int()函数可指定第二个参数从而将其它进制转换为十进制。或许后者…...
RT-Thread 瑞萨 智能家居网络开发:RA6M3 HMI Board 以太网+GUI技术实践
不用放大了, 我在包里找到张不小的…… 以太网HMI线下培训-环境准备 这是社群的文档:【腾讯文档】以太网线下培训(HMI-Board) https://docs.qq.com/doc/DY0FIWFVuTEpORlNn 先介绍周六的培训是啥,然后再介绍一下要准…...

力扣刷题第十天 美丽塔 一
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。 你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。 如果以下条件满足,我们称这些塔是 美丽 的: 1 < heights[i] < maxHeights[i]heights 是一个 山脉…...

c# ADODB.Recordset实例调用Fields报错
代码: using System; using System.CodeDom; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using ADODB;namespace ConsoleApp1 {internal class Programre{static ADODB.Recordset recordsetInstance…...
windows和linux下SHA1,MD5,SHA256校验办法
今天更新android studio到Android Studio Hedgehog | 2023.1.1时,发现提示本机安装的git版本太老,于是从git官网下载最新的git。 git下载地址: https://git-scm.com/ 从官网点击下载最新windows版本会跳转到github仓库来下载发布的git&…...

高新技术企业申报需要具备哪些条件?
(一)企业申请认定时须注册成立一年以上; (二)企业通过自主研发、受让、受赠、并购等方式,获得对其主要产品(服务)在技术上发挥核心支持作用的知识产权的所有权; &#…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
