2023春秋杯冬季赛 --- Crypto wp

前言

比赛没打，赛后随便做一下题目

Crypto

not_wiener

task.py:

from Crypto.Util.number import *
from gmpy2 import *
import random, os
from hashlib import sha1
from random import randrange
flag=b''
x = bytes_to_long(flag)def gen_key():while True:q = getPrime(160)p = 2 * getPrime(1024-160) * q+1if isPrime(p):breakh = random.randint(1, p - 1)g = powmod(h,(p-1)//q, p)y=pow(g,x,p)return p,q,g,y
def cry():a =p = getPrime(512)q = getPrime(512)d = getPrime(280)n = p * qe = inverse(d, (p - 1) * (q - 1))c = pow(a, e, n)return n,e,cp,q,g,y=gen_key()
k1 = random.randint(1, q-1)
h1 = bytes_to_long(sha1(os.urandom(20)).digest())
r1 = pow(g, k1, p) % q
s1 = ((h1 + x*r1) * invert(k1, q))% qn,e,c= cry()a= 
b= 17474742587088593627
k2 = a*k1 + b
h2 = bytes_to_long(sha1(os.urandom(20)).digest())
r2 = pow(g, k2, p) % q
s2 = ((h2 + x*r2) * invert(k2, q)) % q
print(n,e,c)
print(p,q,g,y)
print("h1:%s r1:%s s1:%s"%(h1,r1,s1))
print("h2:%s r2:%s s2:%s"%(h2,r2,s2))

1.txt:

n = 98871082998654651904594468693622517613869880791884929588100914778964766348914919202255397776583412976785216592924335179128220634848871563960167726280836726035489482233158897362166942091133366827965811201438682117312550600943385153640907629347663140487841016782054145413246763816202055243693289693996466579973
e = 76794907644383980853714814867502708655721653834095293468287239735547303515225813724998992623067007382800348003887194379223500764768679311862929538017193078946067634221782978912767213553254272722105803768005680182504500278005295062173004098796746439445343896868825218704046110925243884449608326413259156482881
c = 13847199761503953970544410090850216804358289955503229676987212195445226107828814170983735135692611175621170777484117542057117607579344112008580933900051471041224296342157618857321522682033260246480258856376097987259016643294843196752685340912823459403703609796624411954082410762846356541101561523204985391564p= 161310487790785086482919800040790794252181955976860261806376528825054571226885460699399582301663712128659872558133023114896223014064381772944582265101778076462675402208451386747128794418362648706087358197370036248544508513485401475977401111270352593919906650855268709958151310928767086591887892397722958234379
q= 1115861146902610160756777713087325311747309309771
g= 61073566757714587321114447684333928353300944355112378054603585955730395524359123615359185275743626350773632555967063692889668342544616165017003197599818881844811647270423070958521148291118914198811187731689123176313367399492561288350530256722898205674043032421874788802819858438796795768177550638273020791962
y= 23678147495254433946472657196764372220306841739888385605070426528738230369489739339976134564575544246606937803367113623097260181789372915552172469427842482448570540429192377881186772226796452797182435452490307834205012154495575570994963829345053331967442452842152258650027916313982835119514473311305158299360
(h1, r1, s1) = 535874494834828755542711401117152397489711233142, 117859946800380767356190121030392492081340616512, 26966646740134065096660259687229179143947213779
(h2, r2, s2) = 236574518096866758760287021848258048065293279716, 863199000523521111517835459866422731857447792677, 517924607931342012033031470185302567344725962419

看一眼cry()，d为280bit，n为1024bit，d大概为$n^{0.273}$,wiener的界限为$\frac{1}{3}{n}^{\frac{1}{4}}$,显然超过了wiener的界，而题目名为not_wiener,那就是boneh and durfee了，boneh and durfee的界限为$n^{0.292}$，刚好在其范围内。
简单设置一下参数，设置delta = .273,m = 7

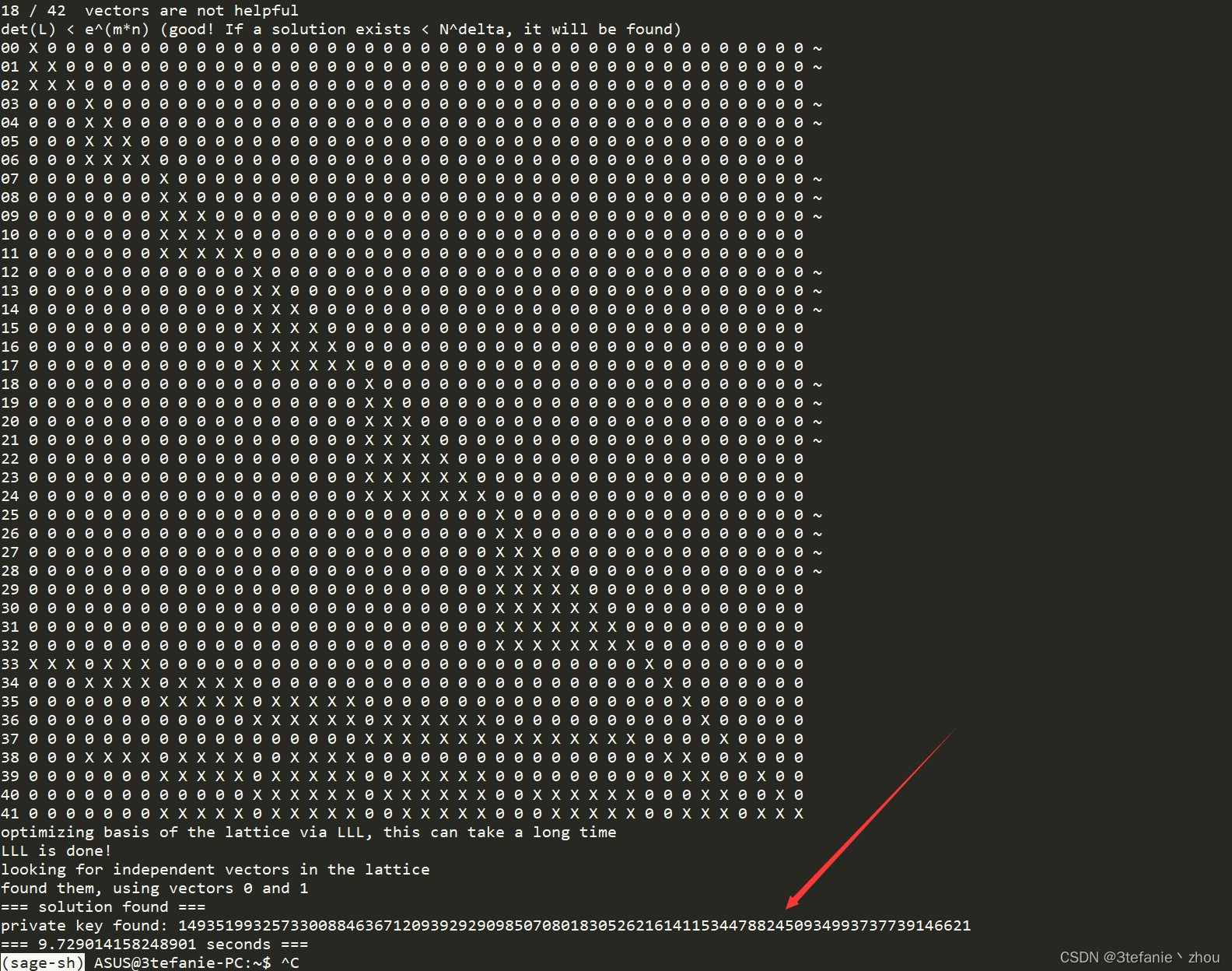
最后带入跑出来的d以及已知的n和c计算得到a

n = 98871082998654651904594468693622517613869880791884929588100914778964766348914919202255397776583412976785216592924335179128220634848871563960167726280836726035489482233158897362166942091133366827965811201438682117312550600943385153640907629347663140487841016782054145413246763816202055243693289693996466579973
e = 76794907644383980853714814867502708655721653834095293468287239735547303515225813724998992623067007382800348003887194379223500764768679311862929538017193078946067634221782978912767213553254272722105803768005680182504500278005295062173004098796746439445343896868825218704046110925243884449608326413259156482881
c = 13847199761503953970544410090850216804358289955503229676987212195445226107828814170983735135692611175621170777484117542057117607579344112008580933900051471041224296342157618857321522682033260246480258856376097987259016643294843196752685340912823459403703609796624411954082410762846356541101561523204985391564
d = 1493519932573300884636712093929290985070801830526216141153447882450934993737739146621
a = pow(c,d,n)
print(a)
#a = 24601959430759983424400804734518943158892550216065342062971649989571838687333

另外一部分，看上去和DSA差不多，主要是等式的变换
此时我们已知$p,q,g,y,h_1,h_2,r_1,r_2,s_1,s_2$，以及有如下等式
$s_1=(h_1+x\ast r_1)\ast k_1^{-1}modq(1)$
$s_2=(h_2+x\ast r_2)\ast k_2^{-1}modq(2)$
$r_1=(g^{k_1}modp)modq$
$r_2=(g^{k_2}modp)modq$
$k_2=a\ast k_1+b$
我们的目的是求出x，但是等式中的k1和k2也是未知的，那么我们就没办法直接求x了。因此我们可以参照DSA，先消除关于x的式子
对于式1，乘上$k_1{r}_2$，得到
$s_1{k}_1{r}_2=r_2(h_1+x\ast r_1)modq$
对于式2，乘上$k_2{r}_1$,得到
$s_2{k}_2{r}_1=r_1(h_2+x\ast r_2)modq$
将$k_2=a\ast k_1+b$带入
$s_2(a\ast k_1+b)r_1=r_1(h_2+x\ast r_2)modq$

两式相减消除x，得到
$s_1{k}_1{r}_2-s_2(a\ast k_1+b)r_1=r_2{h}_1-r_1{h}_{2}modq$
$s_1{k}_1{r}_2-s_{2}a{k}_1{r}_1-s_{2}b{r}_1=r_2{h}_1-r_1{h}_{2}modq$
此时x已经消除,我们的目的是求出k1
再化简一下，得到
$k_1(s_1{r}_2-s_{2}a{r}_1)=r_2{h}_1-r_1{h}_2+s_{2}b{r}_{1}modq$
将$k_1$移到左边
$k_1=(r_2{h}_1-r_1{h}_2+s_{2}b{r}_1)\ast (s_1{r}_2-s_{2}a{r}_1{)}^{-1}modq$
此时式子中的变量都已知，带入即可计算出$k_1$
解出k1，然后带入到$s_1=(h_1+x\ast r_1)\ast k_1^{-1}modq$
化简一下，得到x的等式
$x=(s_1\ast k_1-h_1)\ast r_1^{-1}modq$
最后转换一下x即可得到flag
exp如下：

#sage
p= 161310487790785086482919800040790794252181955976860261806376528825054571226885460699399582301663712128659872558133023114896223014064381772944582265101778076462675402208451386747128794418362648706087358197370036248544508513485401475977401111270352593919906650855268709958151310928767086591887892397722958234379
q= 1115861146902610160756777713087325311747309309771
g= 61073566757714587321114447684333928353300944355112378054603585955730395524359123615359185275743626350773632555967063692889668342544616165017003197599818881844811647270423070958521148291118914198811187731689123176313367399492561288350530256722898205674043032421874788802819858438796795768177550638273020791962
y= 23678147495254433946472657196764372220306841739888385605070426528738230369489739339976134564575544246606937803367113623097260181789372915552172469427842482448570540429192377881186772226796452797182435452490307834205012154495575570994963829345053331967442452842152258650027916313982835119514473311305158299360
(h1, r1, s1) = 535874494834828755542711401117152397489711233142, 117859946800380767356190121030392492081340616512, 26966646740134065096660259687229179143947213779
(h2, r2, s2) = 236574518096866758760287021848258048065293279716, 863199000523521111517835459866422731857447792677, 517924607931342012033031470185302567344725962419
a= 24601959430759983424400804734518943158892550216065342062971649989571838687333
b= 17474742587088593627
k1 = (r2*h1-r1*h2+s2*b*r1)*inverse_mod(s1*r2-s2*a*r1,q)%q
x = (s1*k1-h1)*inverse_mod(r1,q)%q
flag = bytes.fromhex(hex(x)[2:])
print(flag)
#l1near_k1s_unsafe

【所有远游，都是为了重逢。】