【异或哈希】CF855 div3 F
感觉这道题跟之前有一题特别像,都是异或哈希
感觉这种题应该很典,记录一下
(66条消息) Codeforces Round #841 (Div. 2) and Divide by Zero【异或差分+动态map维护】 2022 C. Even Subarrays_lamentropetion的博客-CSDN博客
Problem - F - Codeforces
题意:
给你n个字符串,求对 (i, j) 的数量,使得
c[i] = s[i] + s[j] (两个字符串串联起来)
1.c[i]的长度为奇数
2. c[i] 所包含的字符种类恰好是 25 个
3. c[i] 所包含的每种字符的出现次数都为奇数
思路:
首先,目标状态是不确定的,不知道目标状态少哪个字符,因此我们去枚举少了哪个字符
当2和3都满足时,1一定满足
确定完目标状态之后,注意到我们要去n^2枚举两个指针,那么按照套路的做法,我们去枚举其中一个指针,然后去考虑限定条件来得到另一个指针
它的限定条件和全局的哈希有关,因此我们去维护全局的哈希
那么,全局的哈希去维护什么值呢?很明显是去维护每个字符是否出现以及每个字符的出现次数的奇偶性
a[i]表示每个字符串中每个字符是否出现,b[i]表示每个字符串中字符的出现次数的奇偶性
所以在枚举之前,可以先去预处理这两个哈希
考虑去枚举i,确定了两个字符串连起来的状态,我们怎么去确定j
即s[j]的限定条件是什么
每种字符出现次数为奇数
s[i]和s[j]的字符种类加起来必须有25种
假设 s[i] 对应的 b[i] 是 k,和法的 c[i] 对应的 b[i] 是 q, s[j] 对应的 b[j] 是 p,那 s[i] + s[j] 对应的 b[i] 其实就是 k^p
因此直接去维护动态map就能计数出所有满足条件的对数
当然不能忘记清空cnt数组
Code:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <map>
#include <queue>
#include <set>
//#define int long long
using namespace std;
using i64 = long long;
const int mxn=1e6+10;
const int mxe=1e6+10;
const int mod=1e9+7;string s;
int n;
int a[mxn],b[mxn],cnt[1<<26];
void solve(){s.clear();memset(a,0,sizeof(a));memset(b,0,sizeof(b));memset(cnt,0,sizeof(cnt));cin>>n;for(int i=1;i<=n;i++){cin>>s;for(int j=0;j<s.size();j++){a[i]|=(1<<(s[j]-'a'));b[i]^=(1<<(s[j]-'a'));}}i64 ans=0;for(int i=0;i<26;i++){int S=(1<<26)-1-(1<<i);for(int j=1;j<=n;j++){if(!((a[j]>>i)&1)){cnt[b[j]]++;ans+=cnt[S^b[j]];}}for(int j=1;j<=n;j++){if(!((a[j]>>i)&1)){cnt[b[j]]--;}}}cout<<ans<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;while(__--)solve();return 0;
}相关文章:

【异或哈希】CF855 div3 F
感觉这道题跟之前有一题特别像,都是异或哈希感觉这种题应该很典,记录一下(66条消息) Codeforces Round #841 (Div. 2) and Divide by Zero【异或差分动态map维护】 2022 C. Even Subarrays_lamentropetion的博客-CSDN博客Problem - F - Codeforces题意&a…...

深度学习|改进两阶段鲁棒优化算法i-ccg
目录 1 主要内容 2 改进算法 2.1 CC&G算法的优势 2.2 i-CCG算法简介 3 结果对比 1 主要内容 自从2013年的求解两阶段鲁棒优化模型的列和约束生成算法(CC&G)被提出之后,基本没有实质性的创新,都是围绕该算法在各个领…...

C++11轻松打印本地时间
C11之前,想要获取时间并对其打印是有些困难的,因为C并没有标准时间库。想要对时间进行统计就需要调用C库,并且我们要考虑这样的调用是否能很好的封装到我们的类中。 C11之后,STL提供了 chrono 库,其让对时间的操作更加…...
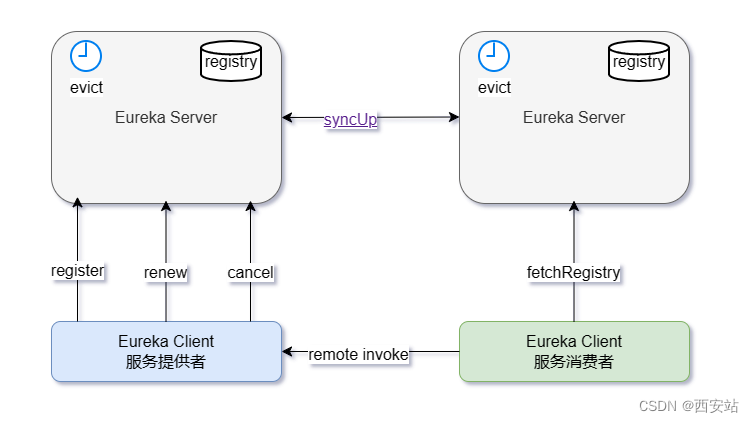
Eureka - 总览
文章目录前言架构注册中心 Eureka Server服务提供者 Eureka Client服务消费者 Eureka Client总结资源前言 微服务(Microservices,一种软件架构风格)核心的组件包括注册中心,随着微服务的发展,出现了很多注册中心的解决…...

【算法设计-枚举、分治】素数、约数、质因数分解
文章目录1. 素数判定2. 素数筛选法3. 质因数分解4. 求一个数的约数5. 求两个数的最大公约数(GCD)6. 求两个数的最小公倍数(LCM)1. 素数判定 判定从 2 到sqrt(n)依次能否把 n 整除,若存在可以整除的数则说明 n 不是素数…...
)
【第十四届蓝桥杯】第三期模拟赛B组C++题解(待修正+持续更新-ing)
文章目录写在前面一、找最小数题目描述解题报告1、大体思路2、代码详解二、求列名题目描述解题报告1、大体思路2、代码详解三、求日期数题目描述解题报告1、大体思路2、代码详解四、取数题目描述解题报告1、大体思路2、代码详解五、最大连通分块题目描述解题报告1、大体思路2、…...
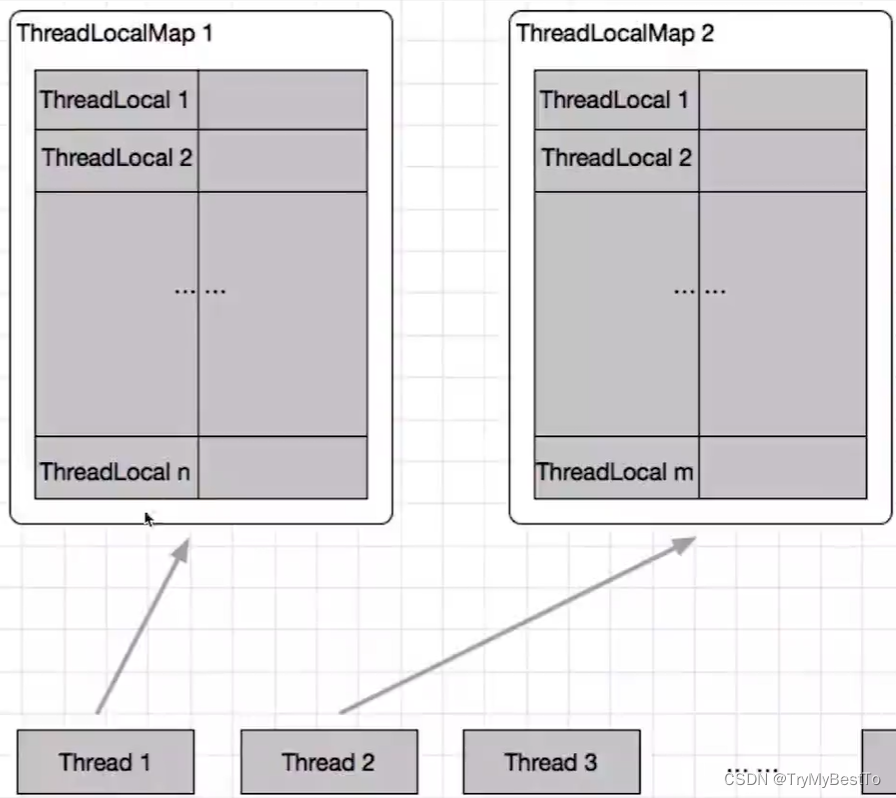
线程池和ThreadLocal详解
线程池和ThreadLocal详解线程池池化模式:线程池里的线程数量设定为多少比较合适?添加线程规则:实现原理:线程池实现任务复用的原理线程池状态:Executors 创线程池工具类手动创建(更推荐):自动创…...
)
[深入理解SSD系列综述 1.7] SSD固态存储市场发展分析与预测_固态存储技术发展方向(2022to2023)
前言 自2020年疫情爆发以来,远程办公、网上教育、流媒体等等应用引爆对消费电子及云服务的需求增长,全球数字化转型加速,带来了两年的闪存风光时刻。然而,进入2022年,在俄乌冲突、疫情重燃、通胀上升等一系列事件冲击下,全球经济下行风险加剧,对智能手机、PC等科技产品的…...
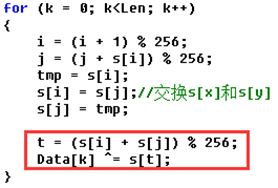
【2021.12.25】ctf逆向中常见加密算法和编码识别
【2021.12.25】ctf逆向中常见加密算法和编码识别(含exe及wp) 文章目录【2021.12.25】ctf逆向中常见加密算法和编码识别(含exe及wp)0、前言1、基础加密手法2、base64(1)原理:(2&#…...

【数据结构初阶】堆排序
目录 前言 概念 堆排序的实现 1.建堆 (1)堆向上调整算法 (2)堆的向下调整算法 2. 利用堆删除思想来进行排序 3.堆排序的时间复杂度 4.源码 总结 前言 前边我们学习了堆的实现,对堆的每个接口都进行了详细的讲…...

Day5: platformDriver-1
Platform Driver (1) Linux kernel中大部分设备可以归结为平台设备,因此大部分的驱动是平台驱动(patform driver) 什么是平台设备 平台设备是linux的设备模型中一类设备的抽象。 内核中的描述: Platform devices are devices t…...

开发手册——一、编程规约_7.控制语句
这篇文章主要梳理了在java的实际开发过程中的编程规范问题。本篇文章主要借鉴于《阿里巴巴java开发手册终极版》 下面我们一起来看一下吧。 1. 【强制】在一个 switch 块内,每个 case 要么通过 break / return 等来终止,要么注释说明程序将继续执行到哪…...
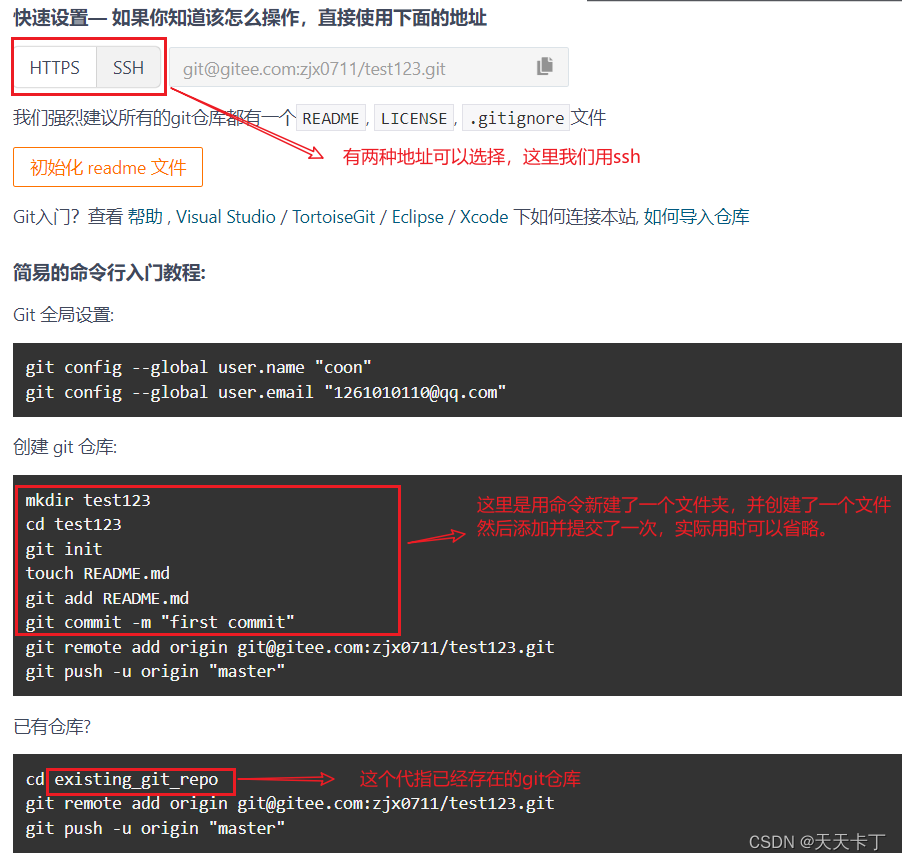
python每日学9 : windows上配置gitee的远程仓库,git的初步使用
在开发中,如果遇到复杂的项目,使用版本控制是非常有必要的,如果涉及到多端开发,那么还需要使用远程仓库。本文作个简单记录,记录下git初步使用。 1 下载与安装 git还有几个ui版本,但是开始使用的话&#…...
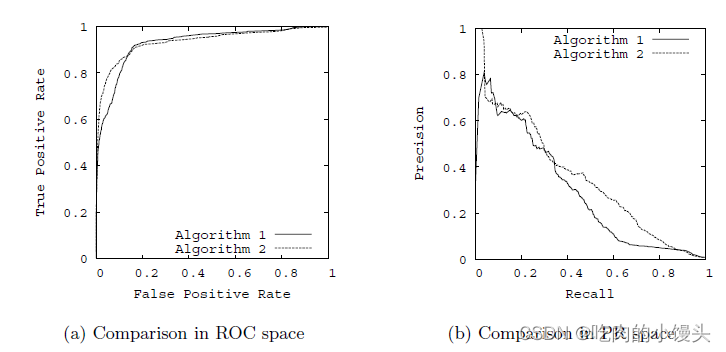
精确率与召回率,ROC曲线与PR曲线
精确率与召回率,ROC曲线与PR曲线 在机器学习的算法评估中,尤其是分类算法评估中,我们经常听到精确率(precision)与召回率(recall),ROC曲线与PR曲线这些概念,那这些概念到底有什么用处呢? 首先,…...
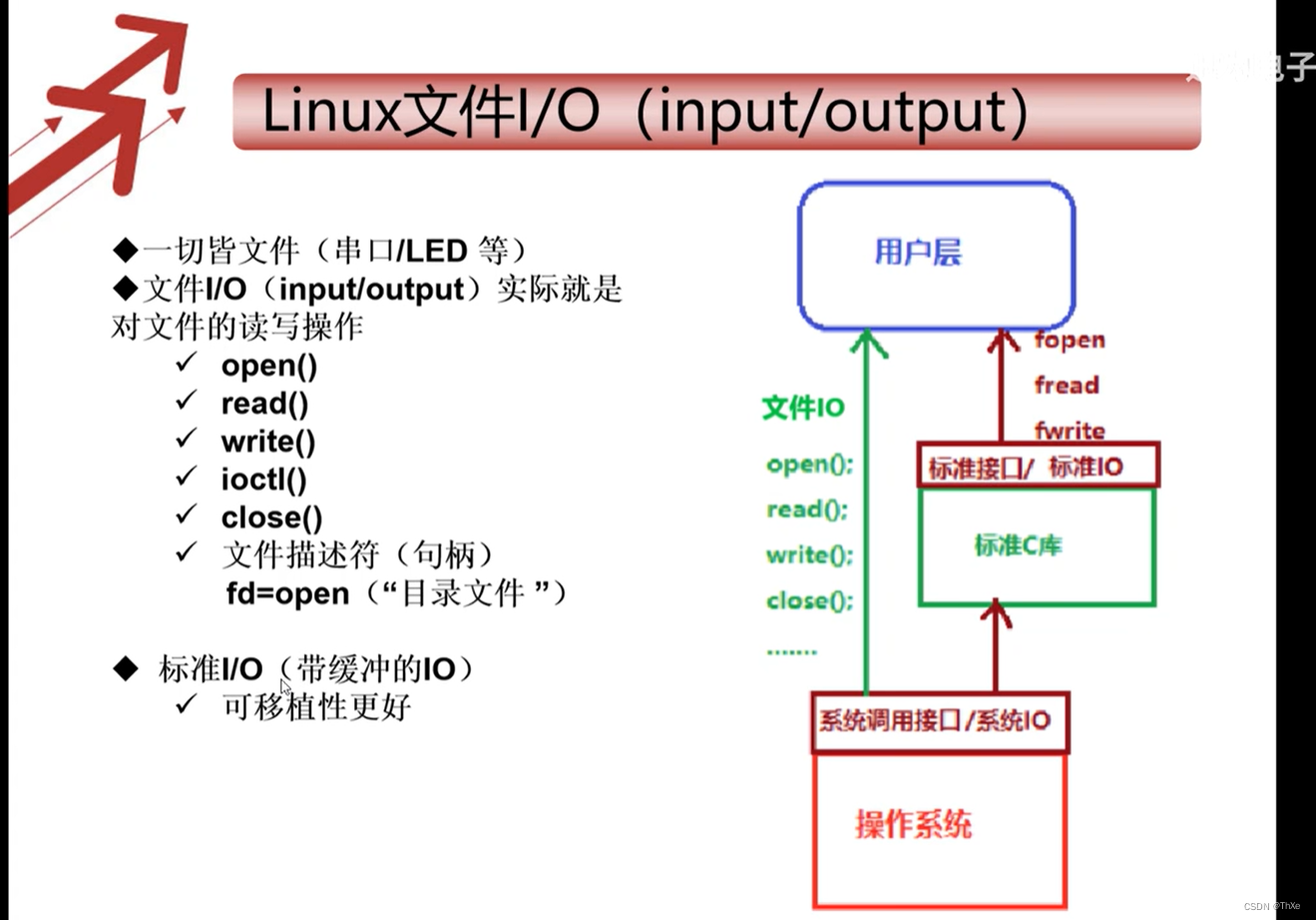
现代操作系统——Linux架构与学习
小白的疑惑 在我决定从事嵌入式(应用层)方面的工作时,我查询了大量资料该如何学习,几乎所有观点不约而同的都指向了学习好Linux,大部分工作都是在Linux环境下来进行工作的。于是我雄心勃勃的去下载Linux,可…...

中文代码82
PK 嘚釦 docProps/PK 嘚釦羸 r docProps/app.xml潙蚽?勶曻Q顗濔S? 錞礖剅D柍珘m?鳞?ぷ辷f硌?2?upc厭Y樐8 rU y搪m眾&a?珪?紓 玺鶋瑣襚? ?i嘲rN?布倖儇?攊橌??嚗猝)芻矂2吟腊K湞?CK臶>鸘\?ΔF滋齢q旮T?桀?;偉 A軥v蕯朾偤佷3?е…...
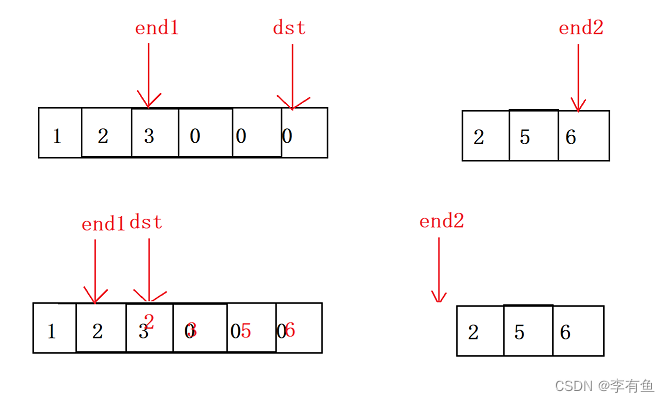
顺序表(一篇带你掌握顺序表)
目录 一、顺序表是什么 1.1 概念 1.2 分类 1.3 结构 二、顺序表的基本操作 2.1 前绪准备 2.2 初始化 2.3 扩容 2.5 尾插 2.6 打印 2.7 尾删 2.8 头插 2.9 头删 2.10 在pos位置插入 2.11 删除pos位置的数据 2.12 查找 三、完整代码 3.1 Test.c文件 3.2 SeqList.h…...
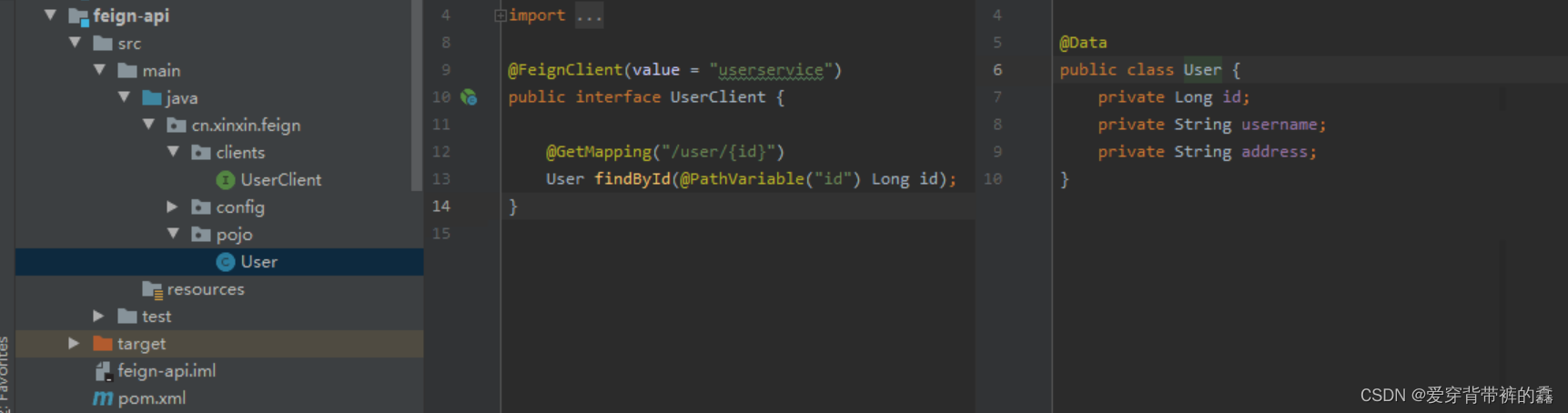
【SpringCloud】SpringCloud教程之Feign实战
目录前言SpringCloud Feign远程服务调用一.需求二.两个服务的yml配置和访问路径三.使用RestTemplate远程调用(order服务内编写)四.构建Feign(order服务内配置)五.自定义Feign配置(order服务内配置)六.Feign配置日志(oder服务内配置)七.Feign调优(order服务内配置)八.抽离Feign前…...
嵌入式linux必备内存泄露检测神器
Valgrind介绍 Valgrind是一个可移植的动态二进制分析工具集,主要用于发现程序中的内存泄漏、不合法内存访问、使用未初始化的内存、不正确的内存释放以及性能问题等,可在Linux和Mac OS X等平台上使用。 Valgrind由多个工具组成,其中最常用的…...

设计模式之行为型模式
四、行为型模式 行为型模式用于描述程序在运行时复杂的流程控制,即描述多个类或对象之间怎样相互协作共同完成单个对象都无法单独完成的任务,它涉及算法与对象间职责的分配。 行为型模式分为类行为模式和对象行为模式,前者采用继承机制来在…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
