LC 2865. 美丽塔 I
2865. 美丽塔 I
难度 : 中等
题目大意
给你一个长度为
n下标从 0 开始的整数数组maxHeights。你的任务是在坐标轴上建
n座塔。第i座塔的下标为i,高度为heights[i]。如果以下条件满足,我们称这些塔是 美丽 的:
1 <= heights[i] <= maxHeights[i]heights是一个 山脉 数组。如果存在下标
i满足以下条件,那么我们称数组heights是一个 山脉 数组:
- 对于所有
0 < j <= i,都有heights[j - 1] <= heights[j]- 对于所有
i <= k < n - 1,都有heights[k + 1] <= heights[k]请你返回满足 美丽塔 要求的方案中,高度和的最大值 。
提示:
1 <= n == maxHeights <= 10^31 <= maxHeights[i] <= 10^9
示例 1:
输入:maxHeights = [5,3,4,1,1]
输出:13
解释:和最大的美丽塔方案为 heights = [5,3,3,1,1] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山脉数组,峰值在 i = 0 处。
13 是所有美丽塔方案中的最大高度和。
分析
根据数据范围可以知道时间复杂度要控制在 O ( n 2 l o g n ) O(n^2logn) O(n2logn),首先我们要确定这个山脉的中心,也就是说我们可以枚举这个中心,然后去构造这个山脉数组,至于怎么构造,因为确定了中心,所以我们可以枚举左右两边,以左边为例,我们要所得的山脉的高度之和最大,所以我们要尽可能取到最大的山脉高度,也就是说,如果当前山脉的最大高度小于等于右边山脉的高度,我们就可以直接取最大的高度,如果比右边的高度高,那么就只能取和右边的山脉相同的高度,右边是同理的,注意数据范围可能爆int,所以注意开long long
暴力枚举
class Solution {
public:using LL = long long;long long maximumSumOfHeights(vector<int>& maxHeights) {int n = maxHeights.size();LL res = 0;for (int i = 0; i < n; i ++){LL sum = maxHeights[i];LL t = maxHeights[i];// 用t表示当前山脉的限制高度for (int j = i - 1; j >= 0; j --)if (maxHeights[j] <= t) sum += maxHeights[j], t = maxHeights[j];else sum += t;t = maxHeights[i];for (int j = i + 1; j < n; j ++)if (maxHeights[j] <= t) sum += maxHeights[j], t = maxHeights[j];else sum += t;res = max(res, sum);}return res;}
};
时间复杂度 O ( n 2 ) O(n^2) O(n2)
分析
我们确定山峰之后,分析左边,从山峰往左看,根据上面的暴力做法的提示,我们发现,假设当前的山峰maxHeight是x,那么如果左边的山脉是高于x的,左边的山脉就会受到限制,那么这个限制什么时候解除呢,碰到一个比x还要小的山脉,而且是第一个,那么我们就可以联想到单调栈的思想,我们可以存下标,我们首先找到受x限制的那一段,终点下标就是栈顶假设是t,那么这一段全部都是x高度,我们定义l[i]表示当前位置为山峰,从i往左看非递增的山脉的高度值和,假设l[i] = l[t] + (i - t) * x(下标从1开始),考虑边界情况,如果左边没有比x小的,那么左边都要受到限制,所以我们可以将栈底始终放一个下标0,这样就方便处理,至于右边的情况,是一样的,我们可以将数组反转一下,然后就是相同的处理
单调栈
class Solution {
public:using LL = long long;long long maximumSumOfHeights(vector<int>& maxHeights) {int n = maxHeights.size();vector<LL> l(n + 1), r(n + 1); // 下标从1开始方便处理边界auto f = [&](vector<LL>& g) {stack<LL> stk;stk.push(0); // 方便处理边界for (int i = 1; i <= n; i ++ ) {while (stk.size() > 1 && maxHeights[stk.top() - 1] >= maxHeights[i - 1]) stk.pop();g[i] = g[stk.top()] + (LL)(i - stk.top()) * maxHeights[i - 1];stk.push(i);}};f(l), reverse(maxHeights.begin(), maxHeights.end()), f(r);LL res = 0;for (int i = 1; i <= n; i ++) {res = max(res, l[i] + r[n - i + 1] - maxHeights[n - i]); // 注意此时数组已经反转了,所以下标要注意}return res;}
};
时间复杂度: O ( n ) O(n) O(n)
结束了
相关文章:

LC 2865. 美丽塔 I
2865. 美丽塔 I 难度 : 中等 题目大意 给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。 你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。 如果以下条件满足,我们称这些塔是 美丽 的: 1 < heights…...
代理设计模式JDK动态代理CGLIB动态代理原理
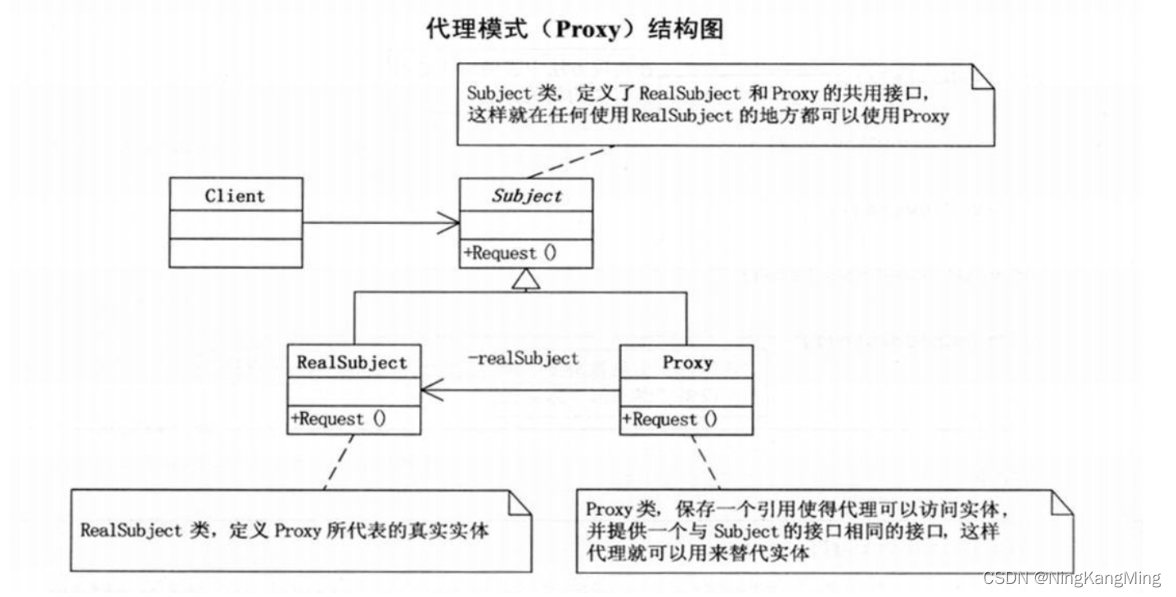
代理设计模式 代理模式(Proxy),为其它对象提供一种代理以控制对这个对象的访问。如下图 从上面的类图可以看出,通过代理模式,客户端访问接口时的实例实际上是Proxy对象,Proxy对象持有RealSubject的引用&am…...
[陇剑杯 2021]webshell
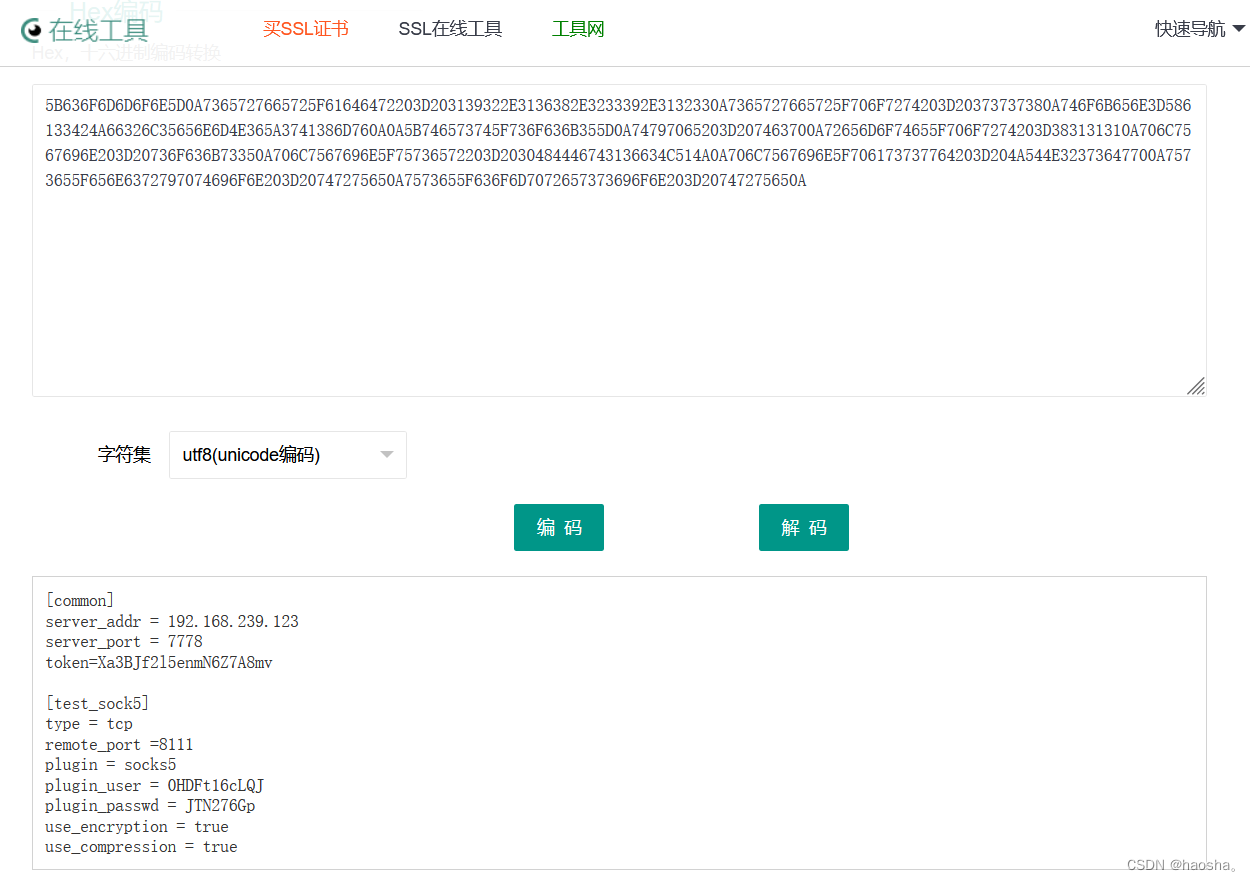
[陇剑杯 2021]webshell 题目做法及思路解析(个人分享) 问一:单位网站被黑客挂马,请您从流量中分析出webshell,进行回答: 黑客登录系统使用的密码是_____________。 题目思路: 分析题目&…...

美易官方:小米汽车交付时间传闻被官方辟谣
在科技与互联网的快速发展浪潮中,各类信息传播速度之快令人咋舌。然而,信息的真实性却时常成为公众关注的焦点。近日,关于小米汽车交付时间的谣言再次引起市场的广泛关注。小米公司发言人迅速作出回应,明确指出这些关于小米汽车交…...

MySQL 简介
什么是MySQL?(熟悉) MySQL是一个开源的、使用标准SQL语言的、可运行于多个系统的、支持多语言的、支持大型数据库的关系型数据库管理系统。由瑞典 MySQL AB 公司开发,目前属于 Oracle 旗下产品。我们通常使用关系型数据库管理系统…...
)
动态规划最后一天(回文串)
目录 647. 回文子串 看到题目的第一想法 看到代码随想录之后的想法 自己实现过程中遇到的困难(看代码) 516.最长回文子序列 看到题目的第一想法 看到代码随想录之后的想法 自己实现过程中遇到的困难(看代码) 647. 回文子串 力扣题目链接…...

c语言之scanf函数
scanf函数语法格式与printf函数很相似,语法是scanf(格式控制,地址列表)组成 其中格式控制分为两部分,一部分由双引号括起来的,%和格式字符组成的格式字符串 普通字符串则是原样输出 地址列表是若干地址组成的表列,可以是变量的…...

ORM-02-JPA Java Persistence API 注解入门介绍
拓展阅读 The jdbc pool for java.(java 手写 jdbc 数据库连接池实现) The simple mybatis.(手写简易版 mybatis) JPA JPA是Java Persistence API的简称,中文名Java持久层API,是JDK 5.0注解或XML描述对象-关系表的映射…...

【MQ01】什么是消息队列?用哪个消息队列?
什么是消息队列?用哪个消息队列? 来了来了,消息队列系列总算来咯。对于搜索引擎相关的知识大家消化的怎么样呀?其实对于搜索引擎来说,我们学习的内容还是挺全面的,也算是比较深入了。而对于消息队列来说&am…...

2023年度AI盘点 AIGC|AGI|ChatGPT|人工智能大模型
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 2023年是人工智能大语言模型大爆发的一年,一些概念和英文缩写也在这一年里集中出现,很容易混淆,甚至把人搞懵。 文章目录 前言01 《ChatGPT 驱动软件开…...
【Flink-CDC】Flink CDC 介绍和原理概述
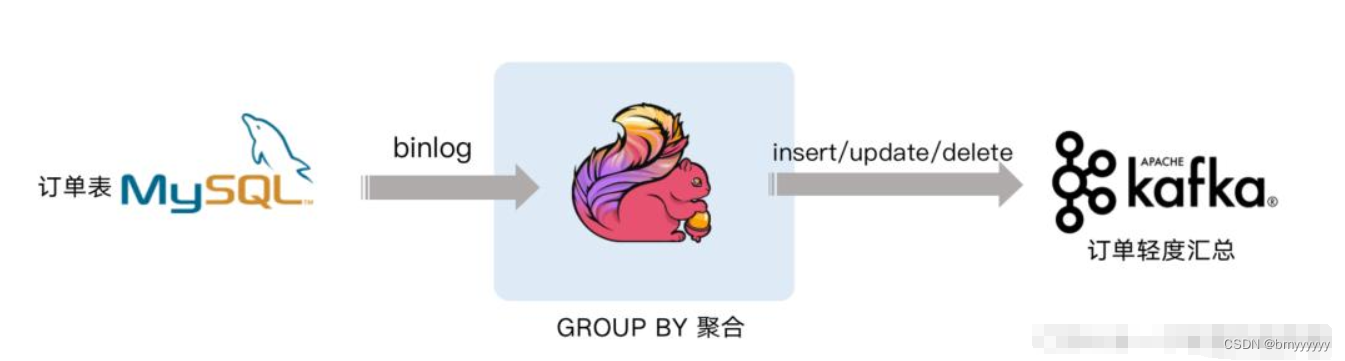
【Flink-CDC】Flink CDC 介绍和原理概述 1)基于查询的 CDC 和基于日志的 CDC2)Flink CDC3)Flink CDC原理简述4)基于 Flink SQL CDC 的数据同步方案实践4.1.案例 1 : Flink SQL CDC JDBC Connector4.2.案例 2 : CDC Streaming ETL…...

长城资产信息技术岗24届校招面试面经
本文介绍2024届秋招中,中国长城资产管理股份有限公司的信息技术岗岗位一面的面试基本情况、提问问题等。 10月投递了中国长城资产管理股份有限公司的信息技术岗岗位,所在部门为长城新盛信托有限责任公司。目前完成了一面,在这里记录一下一面经…...
【计算机网络】TCP握手与挥手:三步奏和四步曲
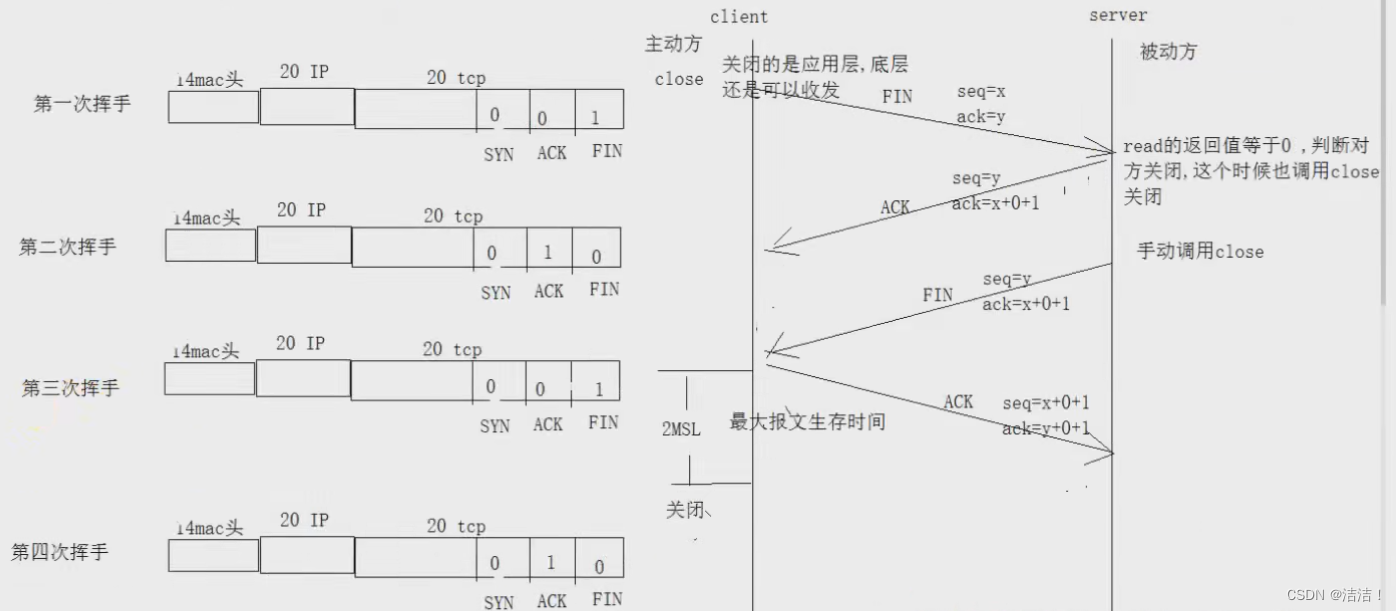
这里写目录标题 前言三次握手四次挥手三次握手和四次挥手的作用TCP三次握手的作用建立连接防止已失效的连接请求建立连接防止重复连接 TCP四次挥手的作用:安全关闭连接避免数据丢失避免半开连接 总结: 总结 前言 TCP(传输控制协议)…...

设计模式学习总结
责任链模式 使用方法: 1.创建接口 2.定义实现类,每个实现类实现接口,并拥有一个ArchiveHandle的成员,用作责任链的链接 public interface ArchiveHandle {void handle(ArchiveVO archiveVO); } public class ArchivePreHandle i…...

「HDLBits题解」Cellular automata
本专栏的目的是分享可以通过HDLBits仿真的Verilog代码 以提供参考 各位可同时参考我的代码和官方题解代码 或许会有所收益 题目链接:Rule90 - HDLBits module top_module(input clk,input load,input [511:0] data,output [511:0] q );always (posedge clk) begin…...

什么是API ?
API(应用程序编程接口) 就像现成的家具套件相对于家居建设,用一些已经切好的木板组装一个书柜,显然比自己设计,寻找合适的木材,裁切至合适的尺寸和形状,找到正确尺寸的螺钉,然后再组…...

Pytest中conftest.py的用法
Pytest中conftest.py的用法 在官方文档中,描述conftest.py是一个本地插件的文件,简单的说就是在这个文件中编写的方法,可以在其他地方直接进行调用。 注意事项 只能在根目录编写conftest.py 插件加载顺序在搜集用例之前 基础用法 这里…...

java.lang.IllegalArgumentException: When allowCredentials is true
1.遇到的错误 java.lang.IllegalArgumentException: When allowCredentials is true, allowedOrigins cannot contain the special value "*" since that cannot be set on the "Access-Control-Allow-Origin" response header. To allow credentials to a…...

vue折叠展开transition动画使用keyframes实现
需求,我正常的菜单功能有隐藏与显示功能,需要增加动画 打开的时候宽度从0到300,关闭的时候,宽度从300到0 <template> <div id"app"> <button click"toggleLength">Toggle Length</bu…...
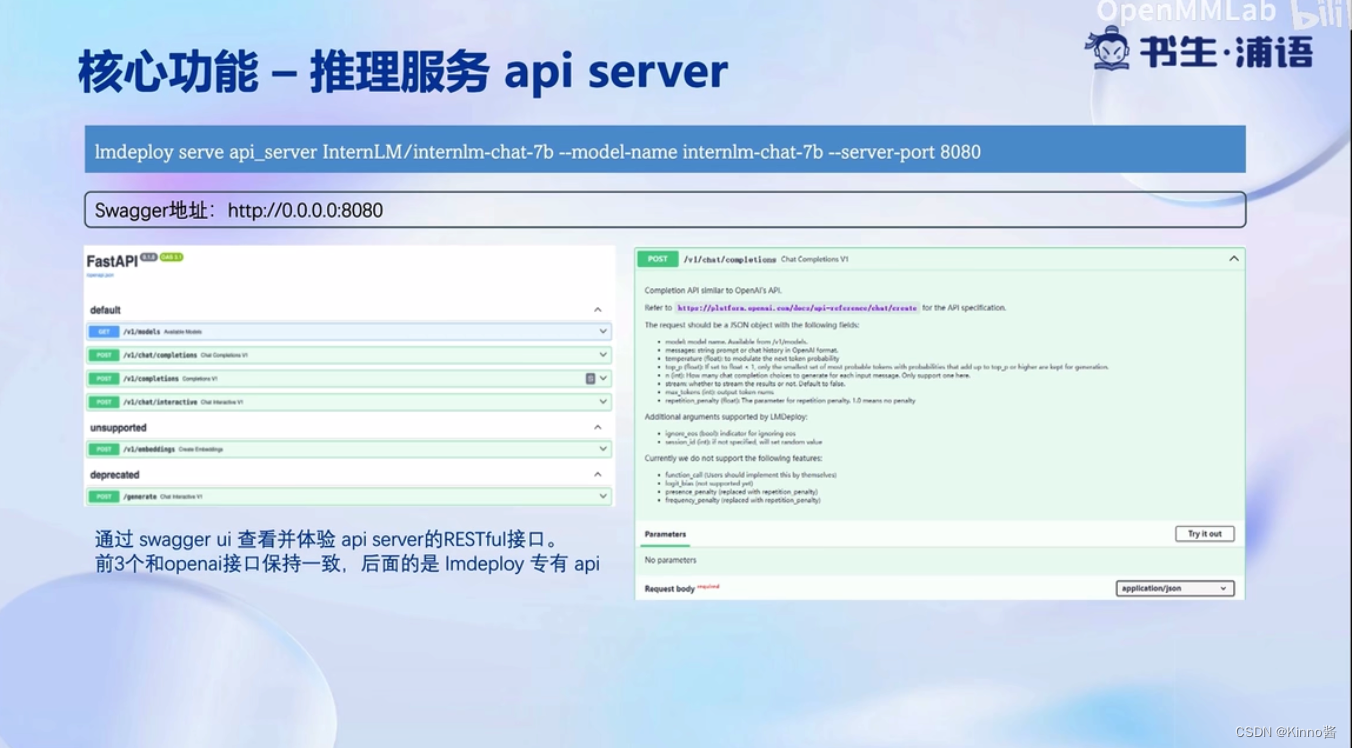
书生·浦语大模型实战营-学习笔记5
LMDeploy 大模型量化部署实践 大模型部署背景 LMDeploy简介 轻量化、推理引擎、服务 核心功能-量化 显存消耗变少了 大语言模型是典型的访存密集型任务,因为它是decoder-by-decoder 先把数据量化为INT4存起来,算的时候会反量化为FP16 AWQ算法&a…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
