当前位置： 首页 > news >正文

【JavaWeb】MVC架构模式

news 2026/2/10 2:51:24

文章目录

  • MVC是什么？
  • 一、M ：Model 模型层
  • 二、V：View 视图层
  • 三、C：Controller 控制层
  • 四、非前后端分离MVC
  • 五、前后端分离MVC
  • 总结

MVC是什么？

MVC（Model View Controller）是软件工程中的一种**软件架构模式**，它把软件系统分为 模型 、 视图 和 控制器 三个基本部分。用一种业务逻辑、数据、界面显示分离的方法组织代码，将业务逻辑聚集到一个部件里面，在改进和个性化定制界面及用户交互的同时，不需要重新编写业务逻辑。

一、M ：Model 模型层

具体功能：

  1. 存放和数据库对象的实体类以及一些用于存储非数据库表完整相关的VO对象
  2. 存放一些对数据进行逻辑运算操作的的一些业务处理代码

项目常见包：

  • 实体类包(pojo /entity /bean)
    • 专门存放和数据库对应的实体类和一些VO对象
  • 数据库访问包(dao/mapper)
    • 专门存放对数据库不同表格CURD方法封装的一些类
  • 服务包(service)
    • 专门存放对数据进行业务逻辑运算的一些类

二、V：View 视图层

具体功能：

  1. 存放一些视图文件相关的代码 html css js等
  2. 在前后端分离的项目中,后端已经没有视图文件,该层次已经衍化成独立的前端项目

项目常见包：

控制层包(controller)

三、C：Controller 控制层

具体功能：

  1. 接收客户端请求,获得请求数据
  2. 将准备好的数据响应给客户端

项目常见包：

  • web目录下的视图资源 html css js img 等
  • 前端工程化后,在后端项目中已经不存在了

四、非前后端分离MVC

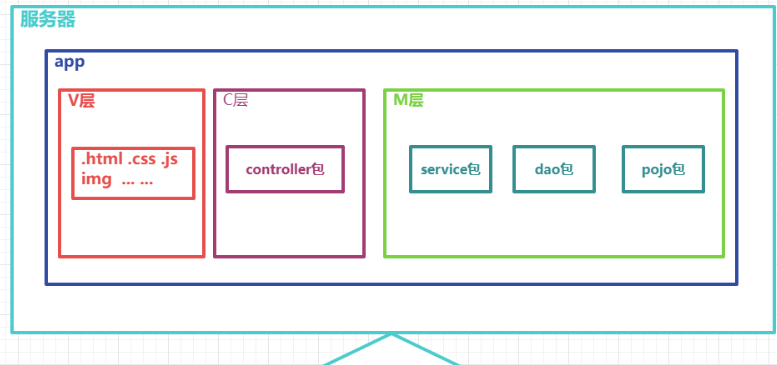
在这里插入图片描述

五、前后端分离MVC

2

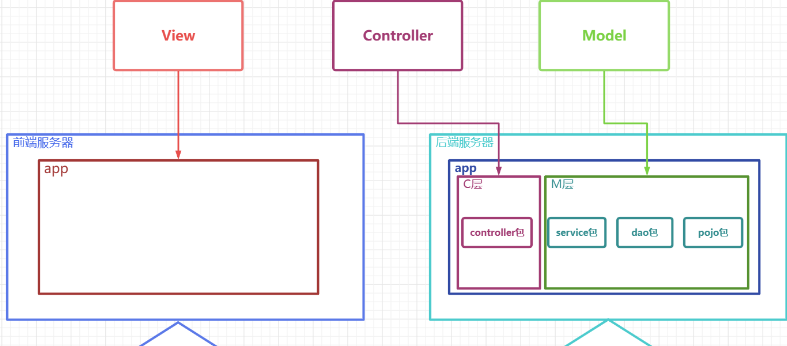
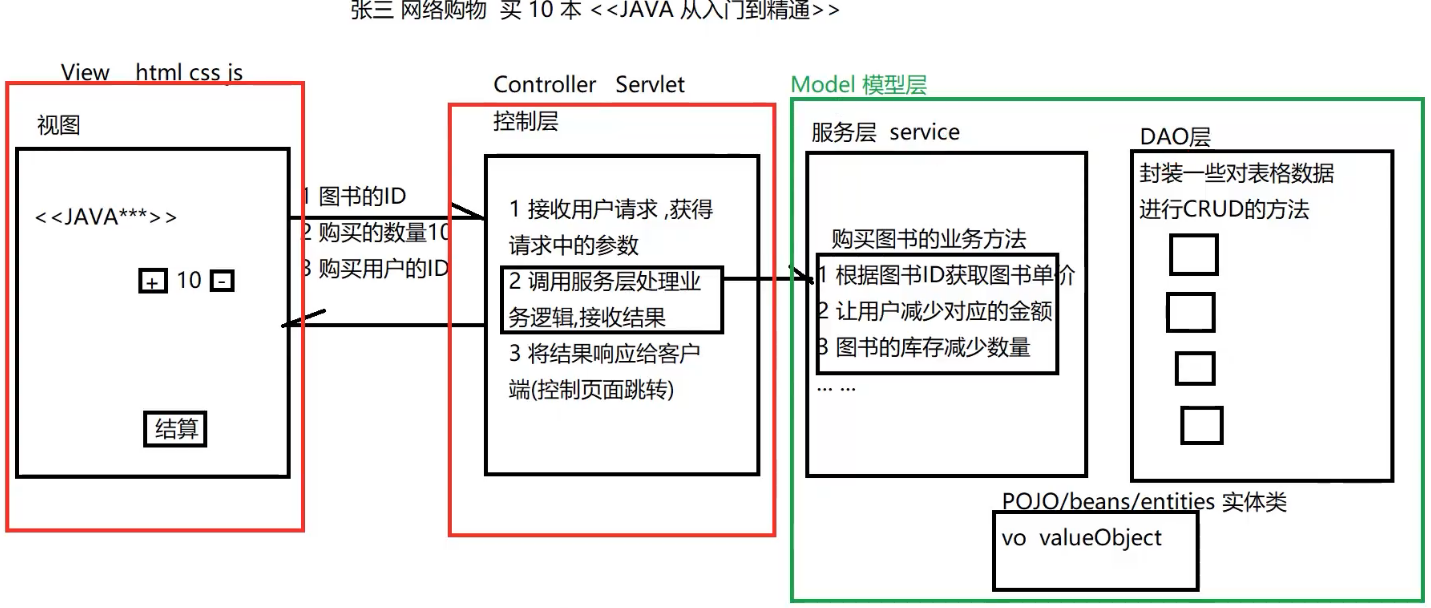
总结

1

相关文章：

【JavaWeb】MVC架构模式

文章目录 MVC是什么？一、M ：Model 模型层二、V：View 视图层三、C：Controller 控制层四、非前后端分离MVC五、前后端分离MVC总结 MVC是什么？ MVC（Model View Controller）是软件工程中的一种**软件…...

编程日记 2024/1/25 8:43:37

【Unity学习笔记】创建人物控制器

人物左右移动 1 导入模型，如果没有模型，则在 窗口-资产商店-free sample 找到人物模型 2 在 窗口-包管理中 导入自己的模型 3 在自己的资产文件夹中找到Prefabs Base HighQuality MaleFree1模型，导入到场景中 4 Assets中创建C#项目 写入如下…...

编程日记 2024/1/25 8:41:34

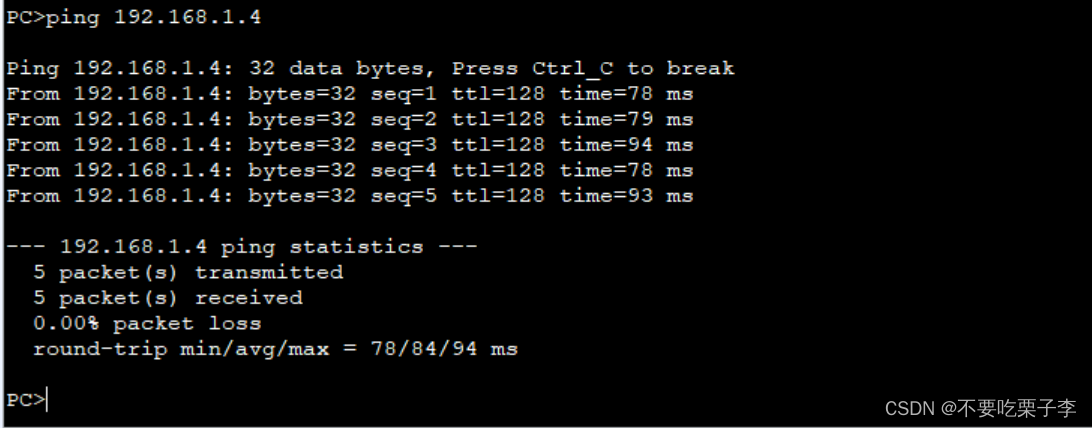
HCIP：不同VLAN下实现网络互相通信

配置pc1 配置pc2 配置pc3 将sw1划分到vlan3 将sw3划分到vlan3 在sw1上进行缺省 将sw1上（g0/0/1）的untagged改成 1 3 则在pc1上ping pc2可通 在sw1上进行缺省 在sw3上（e0/0/1）打标记 则在pc1上ping pc3可通（实现互通&am…...

编程日记 2024/1/25 8:38:30

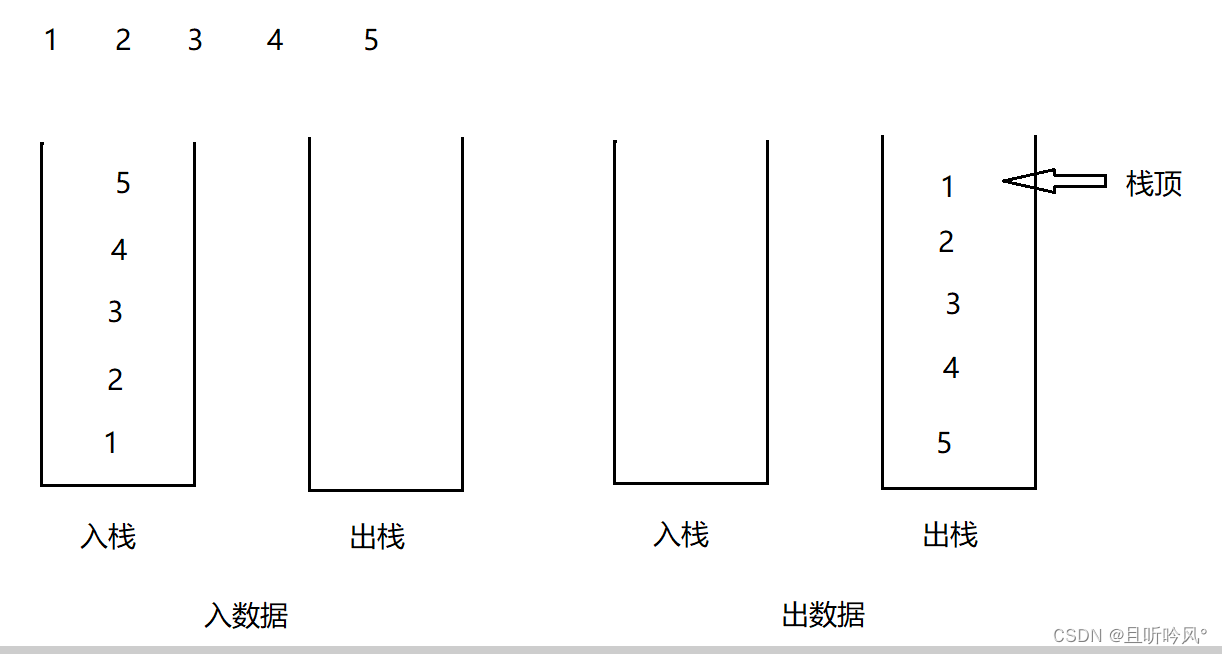
07 队列

目录 1.队列 2.实现 3.OJ题 1. 队列 只允许在一段进行插入数据操作，在另一端进行数据删除操作的特殊线性表，队列具有先进先出FIFO（First In Firtst Out），插入操作的叫队尾，删除操作的叫队头 2. 实现 队列…...

编程日记 2024/1/25 8:37:28

产品面试题2

39.产品经理在与 开发团队合作时，以下哪个角色负责将产品需求转化为可执行的任务？ a) 技术经理 b) 交互设计师 c) 项目经理 d) 开发工程师 答案：c 40.以下哪个方法适用于评估产品的用户满意度和体验？ a) 用户访谈 b) 用户调研问卷…...

编程日记 2024/1/25 8:36:26

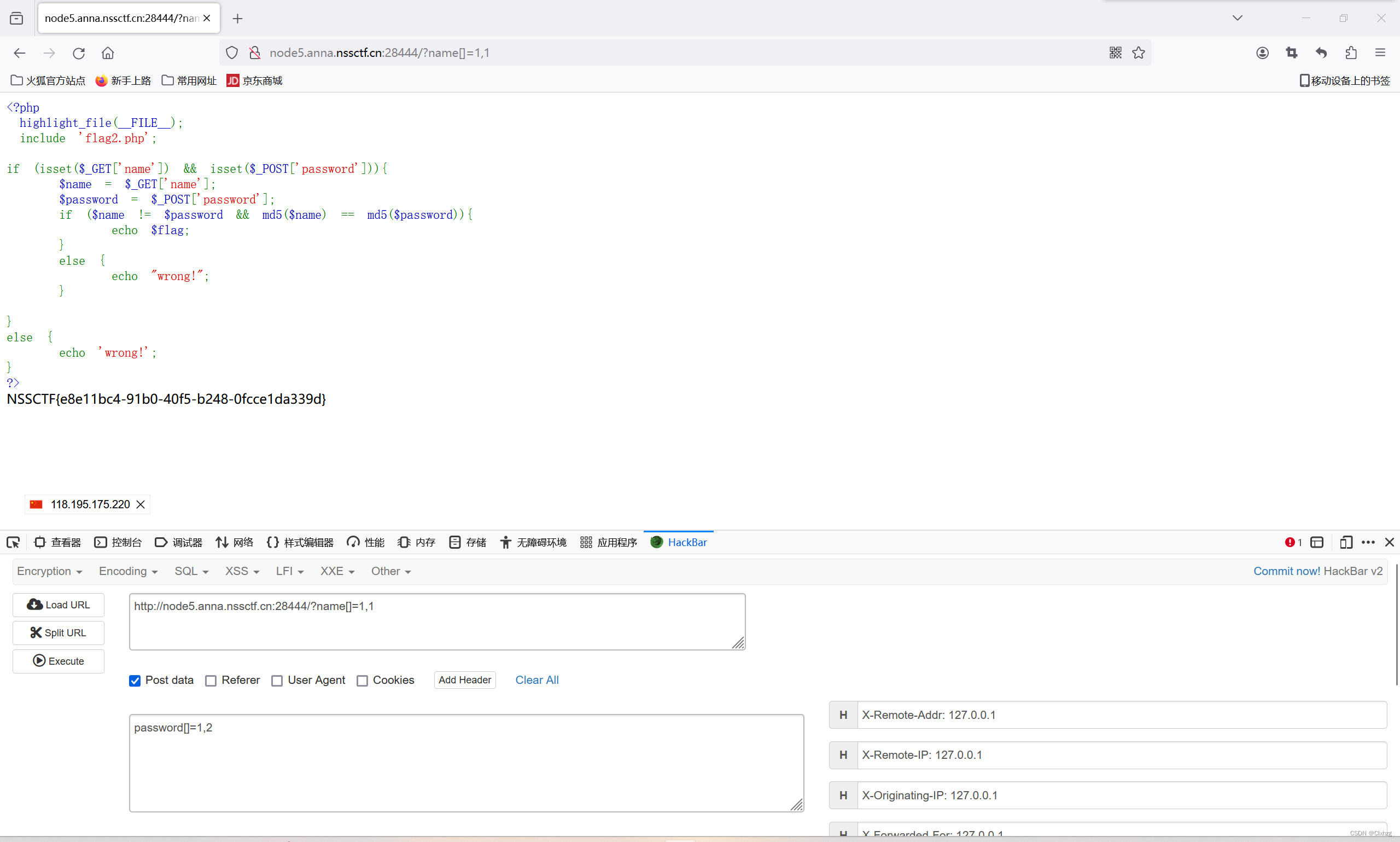
[NSSCTF]-Web:[SWPUCTF 2021 新生赛]easy_md5解析

先看网页 大致就是输入name和password的值，只要他俩的值不一样，然后经过md5函数之后一样就能出flag。 解法一（利用php的科学计数法）： 在php中，假设a，b为数字，那科学计数法可以用ae…...

编程日记 2024/1/25 8:33:23

嵌入式解惑——串口通信中的流控制有什么作用？

在串口通信中，流控制（Flow Control）是一个非常重要的概念。它主要是用来协调发送端和接收端的数据传输速率，以防止接收端流量过大导致的数据丢失问题。   串口通信的特点是数据是以串行方式，一位一位的进行传输。如果…...

编程日记 2024/1/25 8:31:13

Kubernetes-Taint (污点)和 Toleration（容忍）

目录 一、Taint（污点） 1.污点的组成 2.污点的设置、查看和去除 3.污点实验： 二、Toleration（容忍） 1.容忍设置的方案 2.容忍实验： Taint 和 toleration 相互配合，可以用来避免 pod 被分配…...

编程日记 2024/1/25 8:30:12

python三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ，同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意：答案中不可以包含重复的三元组。 示例 1…...

编程日记 2024/1/25 8:27:09

uniapp 用css animation做的鲤鱼跃龙门小游戏

第一次做这种小游戏，刚开始任务下来我心里是没底的，因为我就一个‘拍黄片’的，我那会玩前端的动画啊，后面尝试写了半天，当即我就给我领导说，你把我工资加上去，我一个星期给你做出来，…...

编程日记 2024/1/25 8:26:08

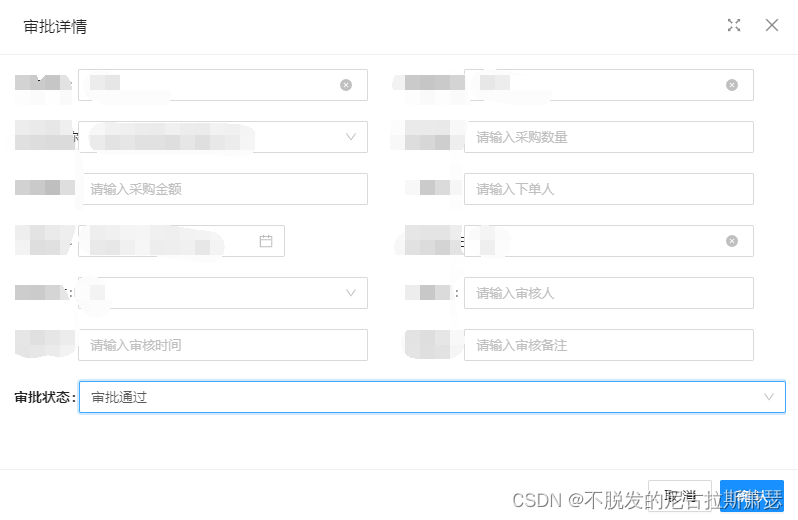
JeecgBoot 3.6.1实现Modal对话框,以为审核数据为例

JeecgBoot 3.6.1实现Modal对话框 vue使用的是3.0版本 文章目录 JeecgBoot 3.6.1实现Modal对话框前言一、列表页面关键代码示例二、textAuditModal.vue代码示例三、test.api.ts总结 前言 在工作中，有一个需求，要求，在数据列表页，…...

编程日记 2024/1/25 8:25:07

Spring基于dynamic-datasource实现MySQL多数据源

目录 多数据源实现 引入依赖 yml配置文件 业务代码 案例演示 多数据源实现 引入依赖 <dependency><groupId>com.baomidou</groupId><artifactId>dynamicdatasourcespringbootstarter</artifactId><version>3.5.0</version> &…...

编程日记 2024/1/25 8:24:06

JS高频面试题（下）

11. 线程和进程的区别 进程是资源分配的最小单元&#xff0c;线程是代码执行的最小单元。 一个应用程序可能会开启多个进程&#xff0c;进程之间数据不共享&#xff0c;一个进程内部可以开启多个线程&#xff0c;线程之间的数据可以共享的&#xff0c;所以多线程的情况下&…...

编程日记 2024/1/25 8:22:04

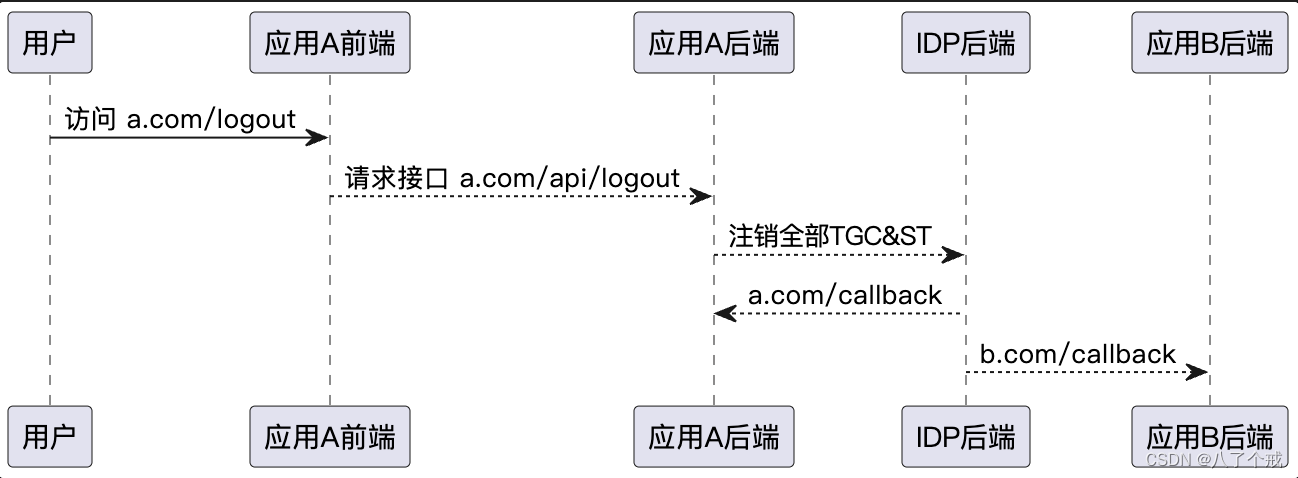
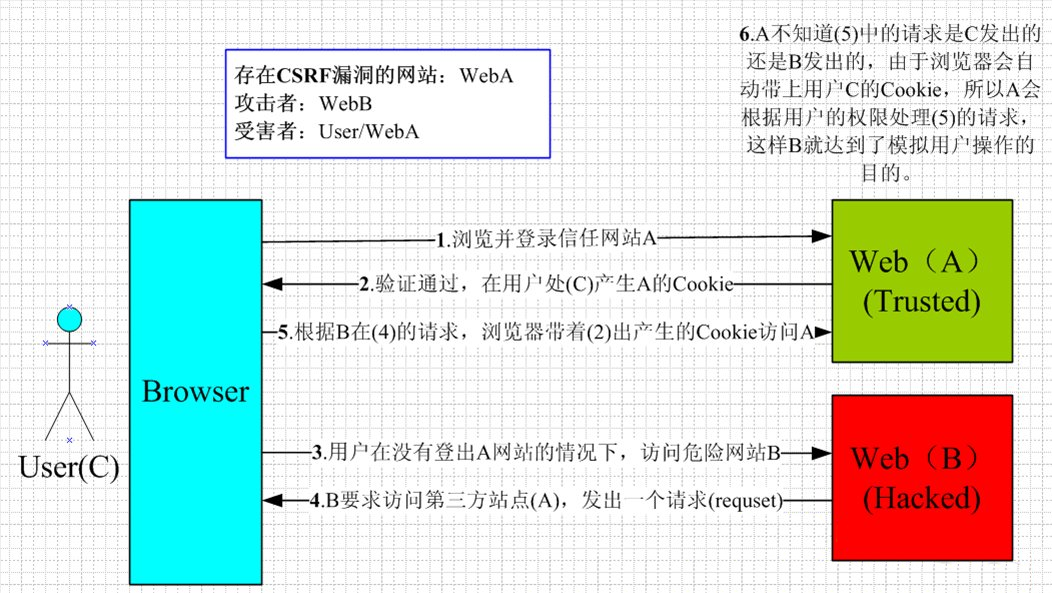
单点登陆（SSO）基于CAS实现前后端分离的SSO系统开发「IDP发起」

关于其他前端常见登录实现单点登录方案&#xff0c;请见「前端常见登录实现方案 单点登录方案 」 前沿 单点登录&#xff08;SSO&#xff09;&#xff0c;英文全称为 Single Sign On。 SSO 是指在多个应用系统中&#xff0c;用户只需要登录一次&#xff0c;就可以访问所有相互…...

编程日记 2024/1/25 8:15:58

二叉树

目录 1翻转二叉树 2对称二叉树 3二叉树的深度 最大深度 最小深度 4二叉树的结点数量 完全二叉树的结点数量 5平衡二叉树 6 中序 后序求前序 二叉树结构体如下&#xff1a; struct freenode {int data;struct freenode *lchild, *rchild;//左孩子 右孩子 }T; 1翻转二…...

编程日记 2024/1/25 8:05:49

边缘计算：挑战与机遇的平衡艺术

前言 边缘计算作为云计算的补充&#xff0c;通过在数据源近处进行数据处理&#xff0c;已经成为实现物联网&#xff08;IoT&#xff09;、自动驾驶、智慧城市等应用的重要技术。然而&#xff0c;边缘计算的发展和普及也面临不少挑战&#xff0c;同时也带来了巨大的机遇。 方向…...

编程日记 2024/1/25 8:03:45

Windows11 Copilot助手开启教程(免费GPT-4)

Windows11上开启Copilot助手教程踩坑指南 Copilot介绍Copilot开启步骤1、更新系统2、更改语言和区域3、下载 ViVeTool 工具4、开启Copilot 使用 Copilot介绍 Windows Copilot 是 Windows 11 中的一个新功能&#xff0c;它可以让你与一个智能助理进行对话&#xff0c;获取信息&…...

编程日记 2024/1/25 8:01:43

【Golang入门教程】如何使用Goland创建并运行项目

自然语言处理的发展 文章目录 自然语言处理的发展**前言**创建新项目编辑运行/调试配置编写并运行代码总结强烈推荐专栏集锦写在最后 前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。点击跳转到网站: 人工…...

编程日记 2024/1/25 8:00:43

鸿蒙开发实战-手写文心一言AI对话APP

运行环境 &#xff08;后面附有API9版本&#xff0c;可修改后在HarmonyOS4设备上运行&#xff09; DAYU200:4.0.10.16 SDK&#xff1a;4.0.10.15 IDE&#xff1a;4.0.600 在DAYU200:4.0.10.16上运行 一、创建应用 1.点击File->new File->Create Progect 2.选择模版…...

编程日记 2024/1/25 7:59:42

鸿蒙常用UI效果及一些处理方式总结

前言&#xff1a; DevEco Studio版本&#xff1a;4.0.0.600 详细使用介绍 1、Text的一些常用设置 Text(this.message).fontSize(50)//字体大小.fontColor(Color.White)//字体颜色.fontWeight(FontWeight.Bold)//字体加粗.backgroundColor(Color.Black)//背景颜色.fontStyle(…...

编程日记 2024/1/25 7:56:38

进程地址空间（比特课总结）

一、进程地址空间 1. 环境变量 1 &#xff09;⽤户级环境变量与系统级环境变量 全局属性&#xff1a;环境变量具有全局属性&#xff0c;会被⼦进程继承。例如当bash启动⼦进程时&#xff0c;环 境变量会⾃动传递给⼦进程。 本地变量限制&#xff1a;本地变量只在当前进程(ba…...

编程新知 2025/11/15 6:48:52

《Qt C++ 与 OpenCV：解锁视频播放程序设计的奥秘》

引言：探索视频播放程序设计之旅 在当今数字化时代，多媒体应用已渗透到我们生活的方方面面，从日常的视频娱乐到专业的视频监控、视频会议系统，视频播放程序作为多媒体应用的核心组成部分，扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上，用户都期望…...

编程新知 2026/2/7 13:17:38

汽车生产虚拟实训中的技能提升与生产优化​

在制造业蓬勃发展的大背景下&#xff0c;虚拟教学实训宛如一颗璀璨的新星&#xff0c;正发挥着不可或缺且日益凸显的关键作用&#xff0c;源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例&#xff0c;汽车生产线上各类…...

编程新知 2026/1/27 7:46:36

抖音增长新引擎：品融电商，一站式全案代运营领跑者

抖音增长新引擎&#xff1a;品融电商&#xff0c;一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中&#xff0c;品牌如何破浪前行&#xff1f;自建团队成本高、效果难控&#xff1b;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

编程新知 2026/2/1 5:45:17

【单片机期末】单片机系统设计

主要内容&#xff1a;系统状态机&#xff0c;系统时基&#xff0c;系统需求分析&#xff0c;系统构建&#xff0c;系统状态流图 一、题目要求 二、绘制系统状态流图 题目&#xff1a;根据上述描述绘制系统状态流图&#xff0c;注明状态转移条件及方向。 三、利用定时器产生时…...

编程新知 2026/1/31 12:27:36

微服务商城-商品微服务

数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

编程新知 2026/1/29 18:30:30

三体问题详解

从物理学角度&#xff0c;三体问题之所以不稳定&#xff0c;是因为三个天体在万有引力作用下相互作用&#xff0c;形成一个非线性耦合系统。我们可以从牛顿经典力学出发&#xff0c;列出具体的运动方程&#xff0c;并说明为何这个系统本质上是混沌的&#xff0c;无法得到一般解…...

编程新知 2025/10/19 5:14:05

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

编程新知 2025/7/4 0:50:01

c++第七天 继承与派生2

这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分&#xff1a;派生类构造函数与析构函数 当创建一个派生类对象时&#xff0c;基类成员是如何初始化的&#xff1f; 1.当派生类对象创建的时候&#xff0c;基类成员的初始化顺序 …...

编程新知 2026/2/2 21:55:02

Sklearn 机器学习 缺失值处理 获取填充失值的统计值

💖亲爱的技术爱好者们，热烈欢迎来到 Kant2048 的博客！我是 Thomas Kant，很开心能在CSDN上与你们相遇～💖 本博客的精华专栏： 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中，数据清…...

编程新知 2026/1/20 10:06:51