diffusion 和 gan 的优缺点对比
- sample速度
- GAN更快,Diffusion需要迭代更多次。
- 训练难度
- GAN 的训练可能是不稳定的,容易出现模式崩溃和训练振荡等问题。
- Diffusion 训练loss收敛性好,比较平稳。
- 模拟分布连续性
- Diffusion相较于GAN可以模拟更加复杂,更加非线性的分布。但是Diffusion模拟的分布没有GAN连续性好,特别是在video风格迁移的时候,可能帧之间的关系会有很大差别。Diffusion就可以建模更加general,复杂的图像,大模型正需要像Diffusion这样的能力。所以SD等cv大模型才会依靠Diffusion越来越强大。
- GAN可以在某种单个类别的生成上做到很好的效果,比如人脸。GAN很难在多种不同类别的图像组成的数据集上学到这样复杂的分布。
- 模型可控性
- 以StyleGAN为代表的GAN,生成器的输入latent space包括noise和latent code(w)。w的存在使得GAN的可控性更加直接,通过控制低维数据就可以控制高维数据的生成(但这种控制更加抽象),比如连续性插值操作和DragGAN等。
- 以SD为代表的Diffusion输入有noise latent space和text embedding space。text embedding的可控性没有w来的直接。
相关文章:

diffusion 和 gan 的优缺点对比
sample速度GAN更快,Diffusion需要迭代更多次。 训练难度GAN 的训练可能是不稳定的,容易出现模式崩溃和训练振荡等问题。Diffusion 训练loss收敛性好,比较平稳。 模拟分布连续性Diffusion相较于GAN可以模拟更加复杂,更加非线性的分…...
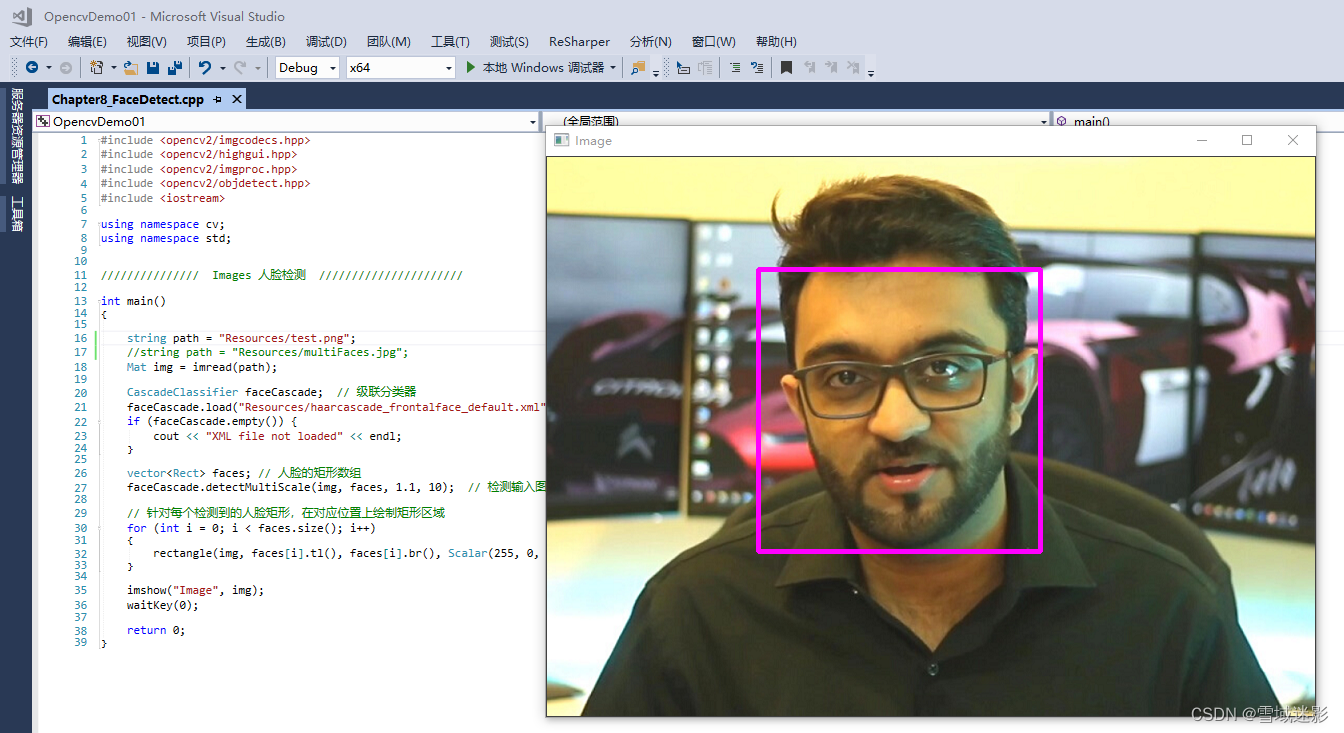
VC++中使用OpenCV进行人脸检测
VC中使用OpenCV进行人脸检测 对于上面的图像,如何使用OpenCV进行人脸检测呢? 使用OpenCV进行人脸检测十分简单,OpenCV官网给了一个Python人脸检测的示例程序, objectDetection.py代码如下: from __future__ import p…...

11Docker数据持久化
Docker数据持久化 容器中数据持久化主要有两种方式: 数据卷(Data Volumes)数据卷容器(Data Volumes Dontainers) 数据卷 数据卷是一个可供一个或多个容器使用的特殊目录,可以绕过UFS(Unix F…...
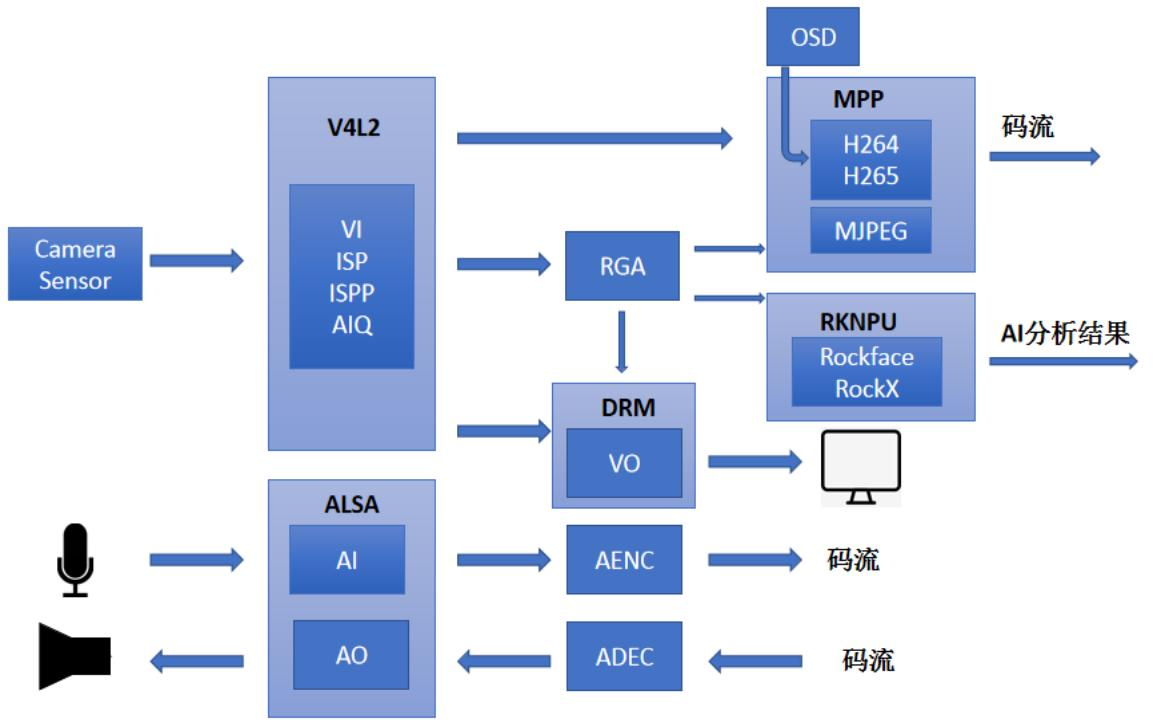
RK3588平台开发系列讲解(视频篇)RKMedia框架
文章目录 一、 RKMedia框架介绍二、 RKMedia框架API三、 视频处理流程四、venc 测试案例沉淀、分享、成长,让自己和他人都能有所收获!😄 📢RKMedia是RK提供的一种多媒体处理方案,可实现音视频捕获、音视频输出、音视频编解码等功能。 一、 RKMedia框架介绍 功能: VI(输…...
Vue3 Teleport 将组件传送到外层DOM位置
✨ 专栏介绍 在当今Web开发领域中,构建交互性强、可复用且易于维护的用户界面是至关重要的。而Vue.js作为一款现代化且流行的JavaScript框架,正是为了满足这些需求而诞生。它采用了MVVM架构模式,并通过数据驱动和组件化的方式,使…...
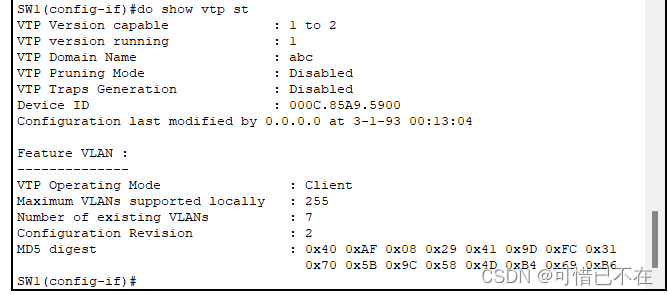
【学网攻】 第(5)节 -- Cisco VTP的使用
文章目录 【学网攻】 第(1)节 -- 认识网络【学网攻】 第(2)节 -- 交换机认识及使用【学网攻】 第(3)节 -- 交换机配置聚合端口【学网攻】 第(4)节 -- 交换机划分Vlan 前言 网络已经成为了我们生活中不可或缺的一部分,它连接了世界各地的人们,让信息和资…...

uniapp复选框 实现排他选项
选择了排他选项之后 复选框其他选项不可以选择 <view class"reportData" v-for"(val, index) in obj" :key"index"> <view v-if"val.type 3" ><u-checkbox-group v-model"optionValue" placement"colu…...

openssl3.2/test/certs - 004 - cross root and root cross cert
文章目录 openssl3.2/test/certs - 004 - cross root and root cross cert概述笔记END openssl3.2/test/certs - 004 - cross root and root cross cert 概述 索引贴 openssl3.2 - 官方demo学习 - test - certs 笔记 // \file my_openssl_linux_log_doc_004.txt // openssl…...
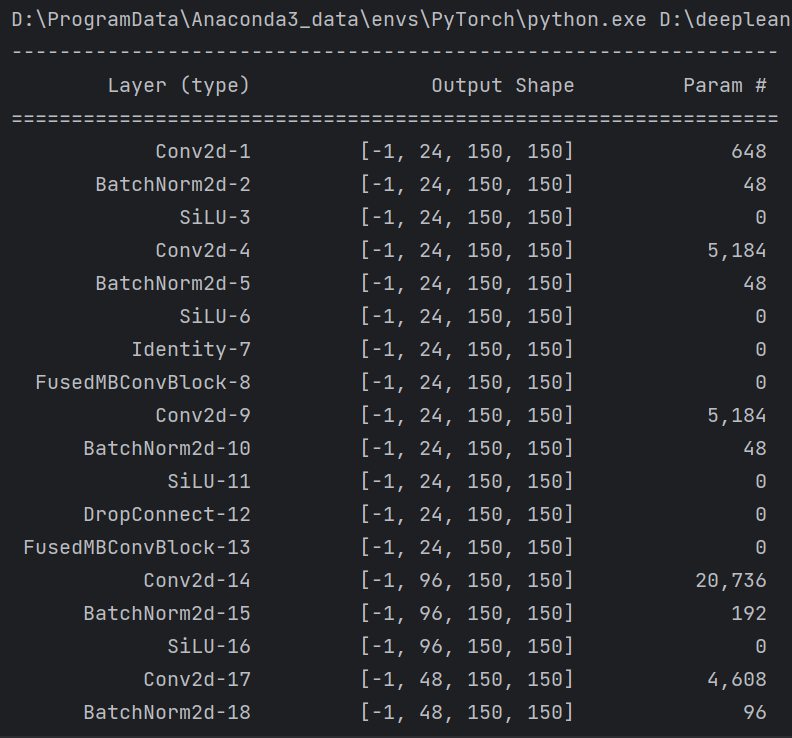
图像分类】【深度学习】【轻量级网络】【Pytorch版本】EfficientNet_V2模型算法详解
【图像分类】【深度学习】【轻量级网络】【Pytorch版本】EfficientNet_V2模型算法详解 文章目录 【图像分类】【深度学习】【轻量级网络】【Pytorch版本】EfficientNet_V2模型算法详解前言EfficientNet_V2讲解自适应正则化的渐进学习(Progressive Learning with adaptive Regul…...

05.Elasticsearch应用(五)
Elasticsearch应用(五) 1.目标 咱们这一章主要学习Mapping(映射) 2.介绍 Mapping是对索引库中文档的约束,类似于数据表结构,作用如下: 定义索引中的字段的名称定义字段的数据类型ÿ…...

npm更换镜像
大家好!今天给大家分享的知识是如何更换npm镜像 前言 有时候在加载npm时有时会很慢,那是由于node安装插件是从国外服务器下载,受网络影响大,速度慢且可能出现异常,这时候就需要更换镜像,使插件的安装快捷&…...
)
野指针(C语言)
野指针 //概念:野指针就是指针指向的位置是不可知的(随机的,不正确的 //,没有明确限制的,空间还属于操作系统而不属于程序的) //野指针成因: //1.指针未初始化 #include <stdio.h> int main() { int* p;//局部变量指针未初始化,默认为随机值 //此时p指向的空间不…...

动物姿态识别(数据集+代码)
动物姿态识别是指利用计算机视觉和深度学习技术来识别动物的姿态,即确定动物身体的姿态、方向和位置等信息。这种技术可应用于动物行为研究、动物健康监测、智能养殖等领域。 动物姿态识别的关键技术包括图像处理、特征提取和分类器设计。首先,需要对动…...
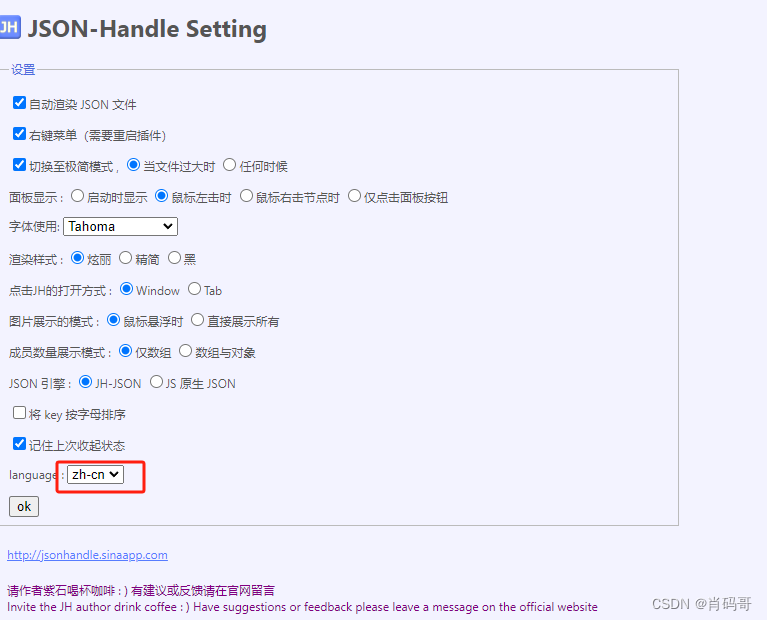
JSON-handle工具安装及使用
目录 介绍下载安装简单操作 介绍 JSON-Handle 是一款非常好用的用于操作json的浏览器插件,对于开发人员和测试人员来说是一款很好用的工具,如果你还没有用过,请赶紧下载安装吧,下面是安装过程和具体使用。 下载安装 点击下载JSON…...
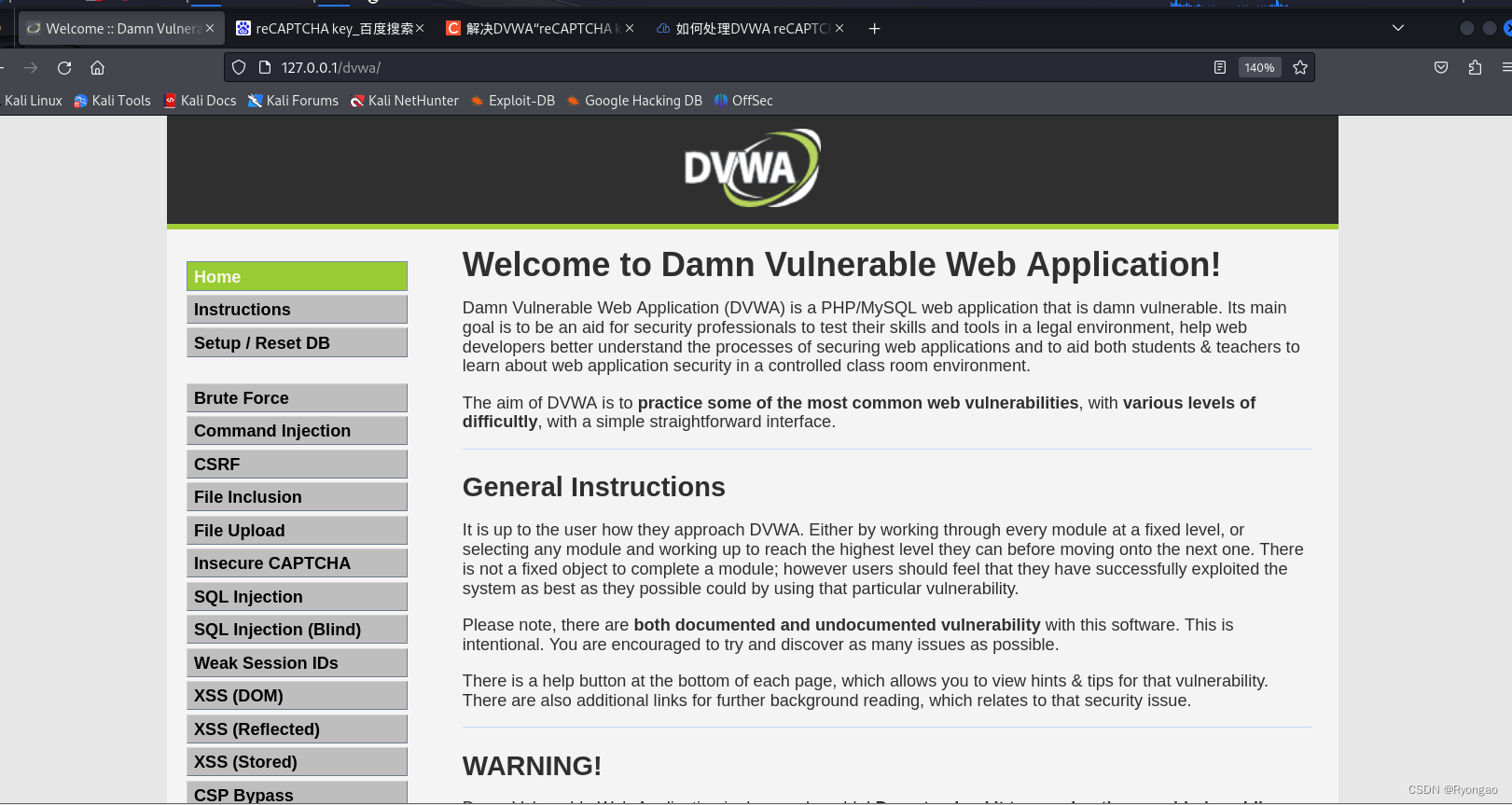
kali安装LAMP和DVWA
LANMP简介 LANMP是指一组通常用来搭建动态网站或者服务器的开源软件,本身都是各自独立的程序,但是因为常被放在一起使用,拥有了越来越高的兼容度,共同组成了一个强大的Web应用程序平台。 L:指Linux,一类Unix计算机操作…...
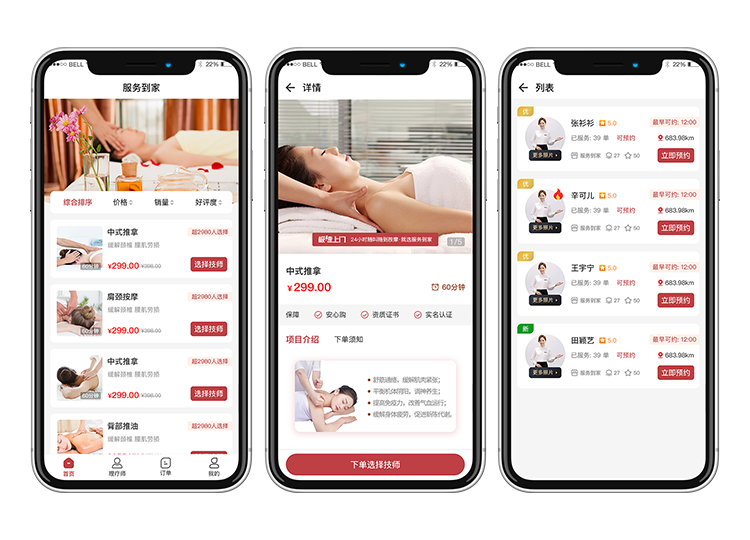
上门服务小程序|预约上门服务系统开发有哪些功能?
在现代快节奏的生活中,压力和疲劳常常困扰着我们。为了缓解这种状况,越来越多的人选择去按摩店进行放松。然而,繁忙的工作和家庭责任往往让我们无法抽出时间去按摩店。在这种情况下,上门按摩服务应运而生。而随着科技的发展&#…...

uniapp vue3版本引用 jsencrypt加密库报错:“default“ is not exported by……
个人产生这个异常的原因:将历史项目(vue2)的jsencrypt文件复制到新项目(vue3)里直接引用报错。存在兼容问题,需要重新安装vue3版本的jsencrypt 安装依赖 npm install jsencrypt页面引入 import { JSEncry…...

【WPF.NET开发】WPF中的双向功能
本文内容 FlowDirectionFlowDocumentSpan 元素非文本元素的 FlowDirection数字替换 与其他任何开发平台不同,WPF 具有许多支持双向内容快速开发的功能,例如,同一文档中混合了从左到右和从右到左的数据。 同时,WPF 也为需要双向功…...
Pytest 测试框架与Allure 测试报告——Allure2测试报告-L3
目录: allure2报告中添加附件-图片 Allure2报告中添加附件Allure2报告中添加附件(图片)应用场景Allure2报告中添加附件(图片)-Python代码示例:allure2报告中添加附件-日志 Allure2报告中添加附件ÿ…...

【机器学习300问】16、逻辑回归模型实现分类的原理?
在上一篇文章中,我初步介绍了什么是逻辑回归模型,从它能解决什么问题开始介绍,并讲到了它长什么样子的。如果有需要的小伙伴可以回顾一下,链接我放在下面啦: 【机器学习300问】15、什么是…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
