【CodeTop】TOP 100 刷题 51-60
文章目录
- 51. 缺失的第一个正数
- 题目描述
- 代码与解题思路
- 52. 训练计划 II
- 题目描述
- 代码与解题思路
- 53. 子集
- 题目描述
- 代码与解题思路
- 54. 最小覆盖子串
- 题目描述
- 代码与解题思路
- 55. 从前序与中序遍历序列构造二叉树
- 题目描述
- 代码与解题思路
- 56. 零钱兑换
- 题目描述
- 代码与解题思路
- 57. 最小栈
- 题目描述
- 代码与解题思路
- 58. 最长有效括号
- 题目描述
- 代码与解题思路
- 59. 反转字符串中的单词
- 题目描述
- 代码与解题思路
- 60. 字符串相乘
- 题目描述
- 代码与解题思路
51. 缺失的第一个正数
题目链接:41. 缺失的第一个正数
题目描述

代码与解题思路
func firstMissingPositive(nums []int) int {for i := 0; i < len(nums); i++ {for nums[i] > 0 && nums[i] <= len(nums) && nums[i] != nums[nums[i]-1] {nums[i], nums[nums[i]-1] = nums[nums[i]-1], nums[i]}}for i := 0; i < len(nums); i++ {if nums[i] != i+1 {return i+1}}return len(nums)+1
}
这道题不难做,难在怎么用 O(N) 的时间复杂读和 O(1) 的空间复杂度来做,如果忽略这两个条件,可以用排序二分,可以用哈希存储
而想要达成这个复杂度的目标,就必须用原地哈希来做,而具体思路就是这个哥们的神之比喻:

52. 训练计划 II
题目链接:LCR 140. 训练计划 II
题目描述

代码与解题思路
func trainingPlan(head *ListNode, cnt int) *ListNode {slow, fast := head, headfor fast != nil && cnt > 0 {fast = fast.Nextcnt--}for fast != nil {slow = slow.Nextfast = fast.Next}return slow
}
这道题刷的次数太多太多,一看到 DNA 都动了,直接快慢指针,fast 先走 cnt 步,然后再一起走就行了。
53. 子集
题目链接:78. 子集
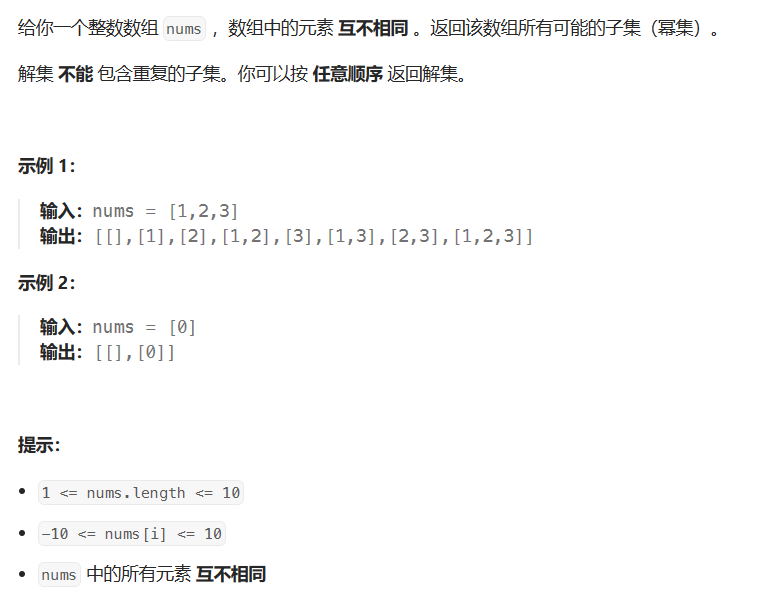
题目描述
代码与解题思路
func subsets(nums []int) (ans [][]int) {tmp := []int{}var dfs func(int)dfs = func(start int) {ans = append(ans, append([]int(nil), tmp...))for i := start; i < len(nums); i++ {tmp = append(tmp, nums[i])dfs(i+1)tmp = tmp[:len(tmp)-1]}}dfs(0)return ans
}
经典的 dfs 模板题,求子集;还有一个模板是 dfs 求全排列,前段时间刷过。
54. 最小覆盖子串
题目链接:76. 最小覆盖子串
题目描述

代码与解题思路
func minWindow(s string, t string) string {if len(s) < len(t) {return ""}win := map[byte]int{}cmp := map[byte]int{}// 初始化 cmpfor i, _ := range t {cmp[t[i]]++}start, end, match, minLen := 0, 0, 0, 100010for left, right := -1, 0; right < len(s); right++ {// 1. 将 s[right] 加入区间ch1 := s[right]win[ch1]++// 2. 更新状态if win[ch1] == cmp[ch1] {match++}// 3. 满足条件, 出窗口for match == len(cmp) {// 更新窗口长度的最小值if right - left < minLen {start, end = left, rightminLen = right - left}// 出窗口, 更新状态left++ch2 := s[left]if win[ch2] == cmp[ch2] {match--}win[ch2]--}}return s[start+1:end+1]
}
这道题是典型的比较复杂的滑动窗口题目,考察对细节的把控,以及对滑动窗口算法思想的掌握程度,省流:考察基本功,我现在基本功也不够扎实,希望下一次能轻松写出这道题目
55. 从前序与中序遍历序列构造二叉树
题目链接:105. 从前序与中序遍历序列构造二叉树
题目描述
代码与解题思路
func buildTree(preorder []int, inorder []int) *TreeNode {if len(preorder) == 0 {return nil}root := &TreeNode{preorder[0], nil, nil}i := 0for i = 0; i < len(inorder); i++ { // 找到与前序遍历数对应的中序遍历数if inorder[i] == preorder[0] {break}}root.Left = buildTree(preorder[1:len(inorder[:i])+1], inorder[:i]) // 构建左子树root.Right = buildTree(preorder[len(inorder[:i])+1:], inorder[i+1:]) // 构建右子树return root
}
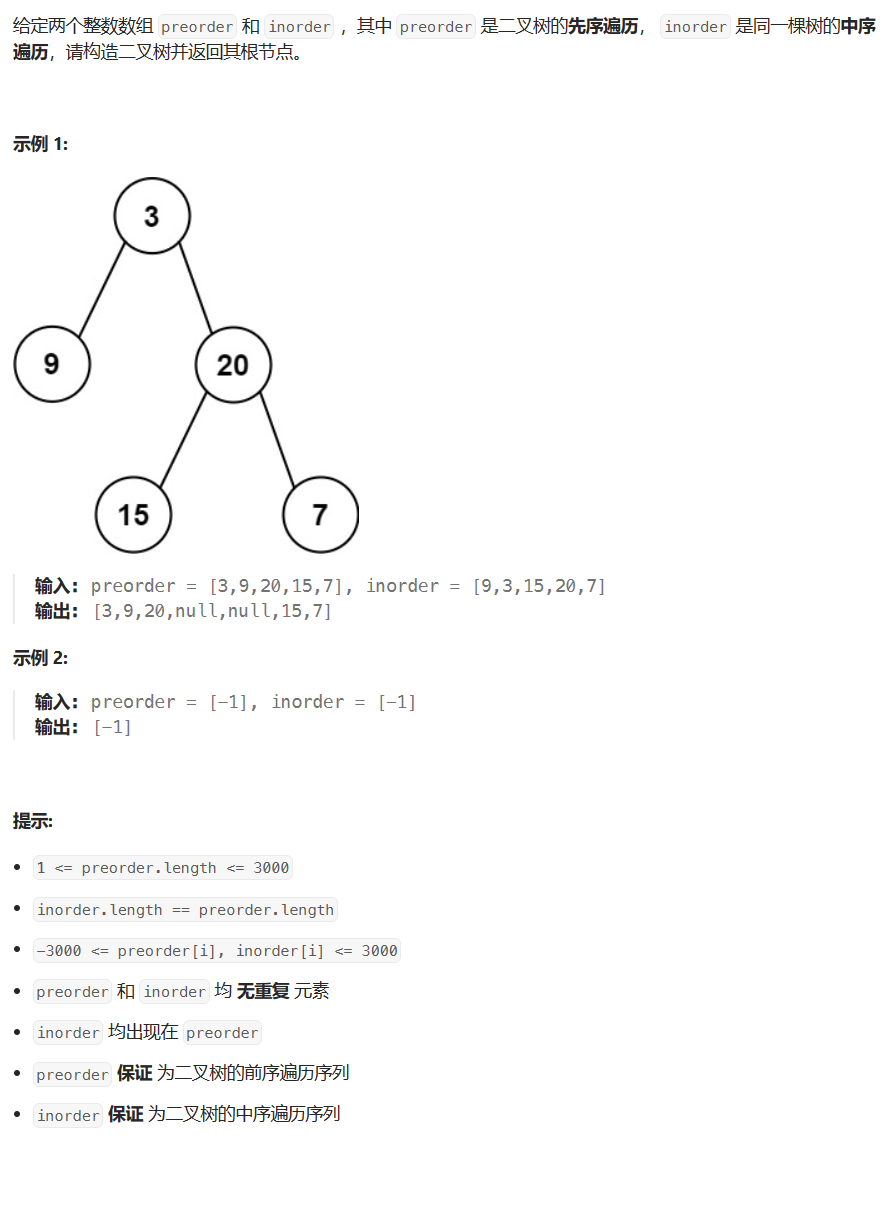
这道题目的关键是得知道怎么用前序遍历和中序遍历的性质推出一棵树,只需要知道这一点,这道题就很好做了,具体来说就是根据两个性质:
- 前序遍历数组的第一个数就是根节点
- 中序遍历数组的数,在左边的就是在他的左子树,在右边就是在他的右子树,举个例子:

根节点 3,中序数组中,9 在 3 的左边,所以他在左子树,剩下的其他节点在右边,所以他们是右子树。
根据这两个性质,就能推出一整棵树了,也通过这个性质来构建一颗树。
56. 零钱兑换
题目链接:322. 零钱兑换
题目描述

代码与解题思路
func coinChange(coins []int, amount int) int {dp := make([]int, amount+1)for i, _ := range dp {dp[i] = math.MaxInt}dp[0] = 0for i := 0; i < len(coins); i++ {for j := coins[i]; j <= amount; j++ {if dp[j-coins[i]] != math.MaxInt {dp[j] = min(dp[j], dp[j-coins[i]]+1)}} }if dp[amount] != math.MaxInt {return dp[amount]}return -1
}
我背包问题没怎么学明白,看的这个哥们的思路:https://leetcode.cn/problems/coin-change/discussion/comments/79896
57. 最小栈
题目链接:155. 最小栈
题目描述

代码与解题思路
这道题真的只有做过才能想的出来,虽然我之前做过一次,但是现在已经忘记了,所以就先凭感觉刷了一遍;
type MinStack struct {arr []int min int
}func Constructor() MinStack {return MinStack{arr: []int{},min: math.MaxInt,}
}func (this *MinStack) Push(val int) {if this.min > val {this.min = val}this.arr = append(this.arr, val)
}func (this *MinStack) Pop() {top := this.arr[len(this.arr)-1]this.arr = this.arr[:len(this.arr)-1]if top == this.min {minVal := math.MaxIntfor _, v := range this.arr {minVal = min(minVal, v)}this.min = minVal}
}func (this *MinStack) Top() int {return this.arr[len(this.arr)-1]
}func (this *MinStack) GetMin() int {return this.min
}
O(1) 取最小,O(N) 维护
之后看了一下官方题解,记忆回归:
type MinStack struct {st1 []intst2 []int
}func Constructor() MinStack {return MinStack {st1: []int{},st2: []int{math.MaxInt},}
}func (t *MinStack) Push(val int) {t.st1 = append(t.st1, val)t.st2 = append(t.st2, min(t.st2[len(t.st2)-1], val))
}func (t *MinStack) Pop() {t.st1 = t.st1[:len(t.st1)-1]t.st2 = t.st2[:len(t.st2)-1]
}func (t *MinStack) Top() int {return t.st1[len(t.st1)-1]
}func (t *MinStack) GetMin() int {return t.st2[len(t.st2)-1]
}
官方给定的方法是,维护两个栈,一个栈正常放值,正常出值;另一个最小栈每次入栈都是最小值
58. 最长有效括号
题目链接:32. 最长有效括号
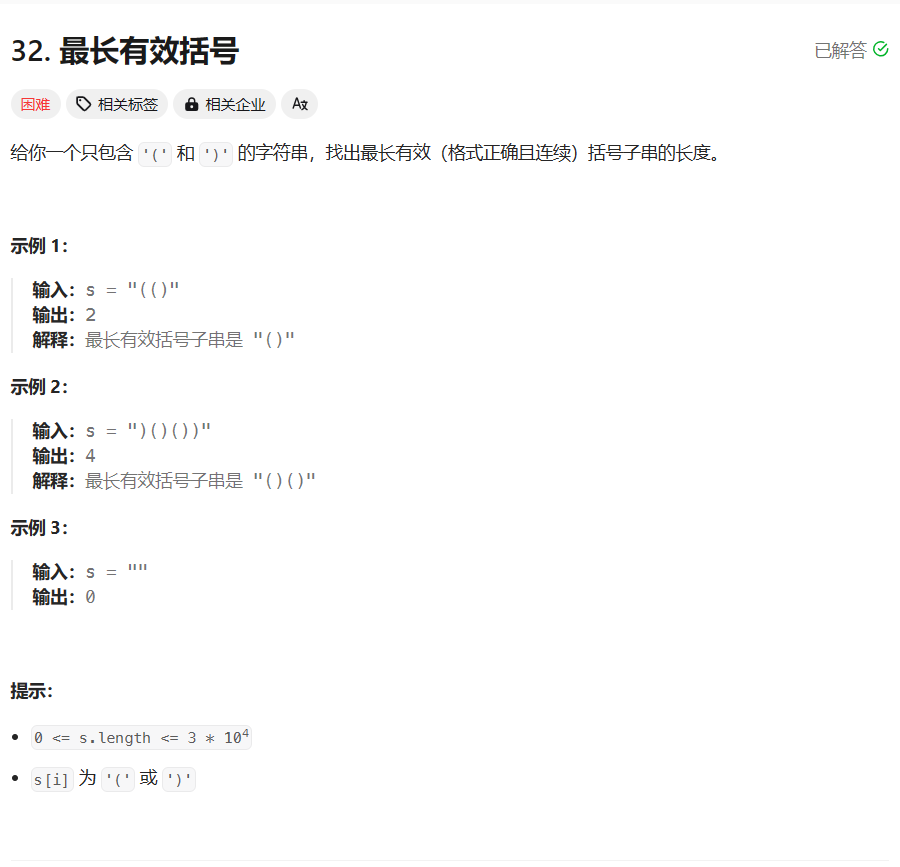
题目描述
代码与解题思路
用栈模拟:
func longestValidParentheses(s string) (ans int) {st := []int{-1}for i, v := range s {if v == '(' {st = append(st, i)} else { // v == ')'st = st[:len(st)-1]if len(st) > 0 { // 栈不为空, 更新最大长度ans = max(ans, i - st[len(st)-1])} else { // 栈为空, 将')'对应的索引入栈作为新的参照物st = append(st, i)}}}return ans
}
核心思想:
- 保留一个参照位置,通过当前索引值 - 参照位置的索引求出最长括号的长度,参照位置初识为 -1,之后为初识位置的前一个位置
- 当 v == ‘(’ 时入栈,遇到 ‘)’ 出栈匹配,并更新最长长度,当遇到 ‘)’ 而没有 ‘(’ 匹配的话,就让它作为新的参照物
其实还有动态规划的解法,但是对我现在来说太难了
59. 反转字符串中的单词
题目链接:151. 反转字符串中的单词
题目描述

代码与解题思路
func reverseWords(s string) string {s = strings.TrimSpace(s)left, right := len(s)-1, len(s)-1resSlice := make([]string, 0)for left >= 0 {// left 找单词左边界for left >= 0 && s[left] != ' ' {left--}resSlice = append(resSlice, s[left+1:right+1])// left 跳过空格for left >= 0 && s[left] == ' ' {left--}right = left}return strings.Join(resSlice, " ")
}
这道题主要是用了 s = strings.TrimSpace(s),以及 strings.Join(resSlice, " ") 两个字符串相关的 api,之后我会总结一份 Golang 专属的刷算法 api 库,到时候会收录进去的
60. 字符串相乘
题目链接:43. 字符串相乘
题目描述

代码与解题思路
func multiply(num1 string, num2 string) string {if num1 == "0" || num2 == "0" {return "0"}ans := "0"m, n := len(num1), len(num2)for i := n - 1; i >= 0; i-- {curr := ""add := 0for j := n - 1; j > i; j-- { // 竖式乘法, 每乘一个数后面会多一个 0curr += "0"}y := int(num2[i] - '0')for j := m - 1; j >= 0; j-- {x := int(num1[j] - '0')product := x * y + addcurr = strconv.Itoa(product % 10) + curr // 把新计算的数拼接到 curr 前面add = product / 10}if add != 0 { // 处理最后一次进位curr = strconv.Itoa(add % 10) + curr}ans = addStrings(ans, curr)}return ans
}func addStrings(num1, num2 string) string { // 竖式乘法的每一轮相加i, j := len(num1) - 1, len(num2) - 1add := 0ans := ""for ; i >= 0 || j >= 0 || add != 0; i, j = i - 1, j - 1 {x, y := 0, 0if i >= 0 {x = int(num1[i] - '0')}if j >= 0 {y = int(num2[j] - '0')}result := x + y + addans = strconv.Itoa(result % 10) + ansadd = result / 10}return ans
}
这道题不简单,但并不是不能做,一定要做好分析,正确的模拟竖式乘法的过程,主要是分为两个步骤,一个是对竖式乘法每一行乘积的模拟,一个是将竖式乘法每一行的乘积相加的模拟,把这两个核心步骤实现了,这道题目就做出来了
考察的是对字符串操作和代码的把控能力,现在我的代码把控能力还没有非常的强,我希望寒假的这一个月能有一个不小的进步
相关文章:

【CodeTop】TOP 100 刷题 51-60
文章目录 51. 缺失的第一个正数题目描述代码与解题思路 52. 训练计划 II题目描述代码与解题思路 53. 子集题目描述代码与解题思路 54. 最小覆盖子串题目描述代码与解题思路 55. 从前序与中序遍历序列构造二叉树题目描述代码与解题思路 56. 零钱兑换题目描述代码与解题思路 57. …...

k8s的图形化工具---rancher
rancher是一个开源的企业级多集群的k8s管理平台。 rancher和k8s的区别:都是为了容器的调度和编排系统。但是rancher不仅可以调度还可以管理整个k8s集群。 rancher自带监控(普罗米修斯) 实验部署 master01 20.0.0.32 node01 20.0.0.34 node02 20.0.0.35 test …...
npm安装卡住问题(最新版)
npm安装卡住问题(最新版) 背景: 最近这两天用npm安装一些包的时候,发现一直卡住: 报错: idealTree:npm: sill idealTree buildDeps之前能用的现在不能用了,我一想,是不是源头的问题,还真是…...
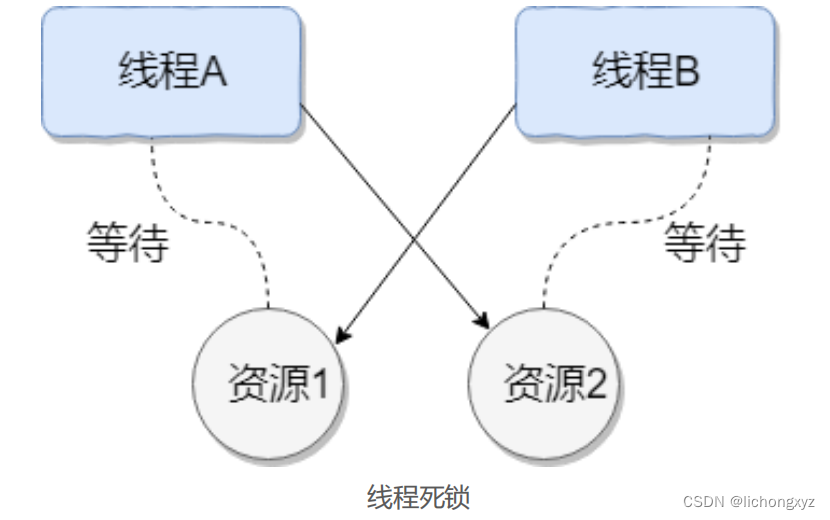
什么是线程死锁
死锁是指两个或两个以上的进程(线程)在执行过程中,由于竞争资 源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推 进下去。此时称系统处于死锁状态或系统产生了死锁,这些永远在互相…...
Django从入门到精通(二)
目录 三、视图 3.1、文件or文件夹 3.2、相对和绝对导入urls 3.3、视图参数requests 3.4、返回值 3.5、响应头 3.6、FBV和CBV FBV 四、静态资源 4.1、静态文件 4.2、媒体文件 五、模板 5.1、寻找html模板 5.2、模板处理的本质 5.3、常见模板语法 5.4、内置模板函…...

建筑物防雷检测安全接地应用解决方案
雷电是一种自然现象,具有极高的电压和电流,对建筑物及其内部设备、人员和财产可能造成严重的危害,如火灾、爆炸、电击、电磁干扰等。因此,建筑物必须采取有效的防雷措施,以保障建筑物的安全和可靠运行。建筑物防雷检测…...
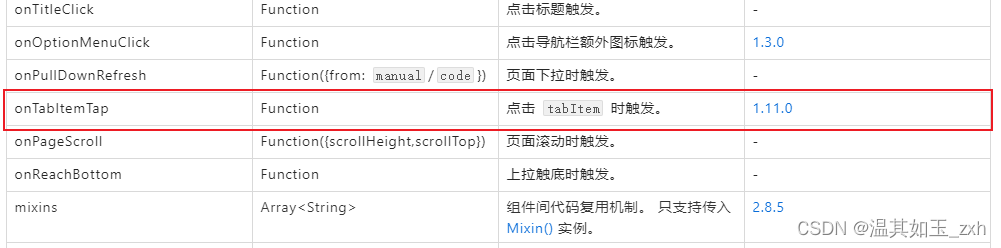
支付宝小程序开发踩坑笔记(支付宝、学习强国小程序)
1、接口请求安卓端回调 success,IOS 端回调 fail 原因:dataType 设置不对,默认是 json 格式,对返回数据会进行 json 解析,如果解析失败,就会回调 fail 。加密传输一般是 text 格式。 2、input 禁止输入空格…...
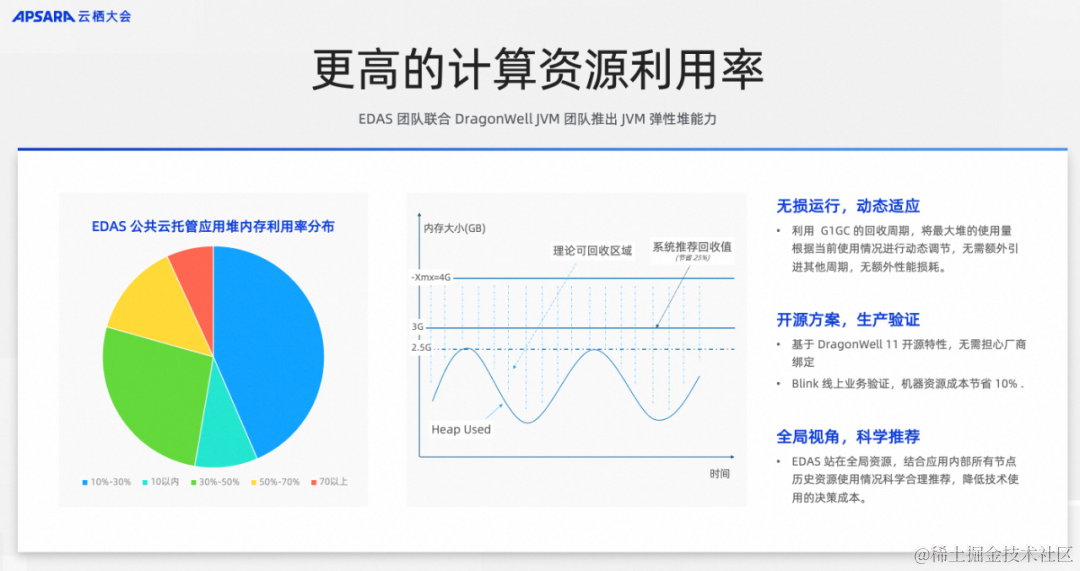
如何降低微服务复杂度丨云栖大会微服务主题分享实录
作者:谢吉宝 本文整理自阿里云资深技术专家、中间件负责人谢吉宝在2023云栖大会《极简微服务模式,降低微服务复杂度的最佳实践》的分享 2023 云栖大会现场 当面临复杂的挑战时,"分而治之"的方法往往能取得显著的效果。微服务架构…...

openresty 安装, nginx与 openresty
openresty VS nginx Nginx 是一款高性能的 Web 服务器和反向代理服务器,具备基础的功能如HTTP服务、负载均衡、反向代理以及动静分离等。它是许多互联网应用的核心组件,因其模块化和可扩展的设计而受到欢迎。1 OpenResty 是基于 Nginx 的 Web 平台&…...

puppeteer实现截图
Window服务器说明 1.在本地安装 puppeteer 先创建一个本地文件夹puppeteer,我的地址D:\common_workspace\puppeteer 然后使用cmd打开这个文件夹所在位置,再执行如下两条命令即可。 npm install -g cnpm --registryhttps://registry.npm.taobao.orgcnpm …...
【2024Java面试突击】并发编程、线程池面试实战
前言 最近在更新面试突击专栏,我把每一篇将字数都尽量控制在 2000 字以内,可能在文章里边写的没有那么细致,主要是提供一些 问题 以及 回答的思路 ,以及 面试中可能忽略的漏洞 ,所以在看完文章之后,如果自…...
ASUS华硕无畏Pro15笔记本电脑(M6500QB,M6500QH)工厂模式原厂OEM预装Windows11.22H2系统 含Recovery恢复
原装出厂Windows11系统适用于华硕无畏15笔记本电脑型号:M6500QB和M6500QH 链接:https://pan.baidu.com/s/1AVGLN6-ILIRogOMj48Mk1w?pwdmi7d 提取码:mi7d 带有ASUS RECOVERY恢复功能、自带所有驱动、出厂主题专用壁纸、系统属性联机支持…...

代码随想录算法训练营第三十天|51. N皇后
|51. N皇后 public List<List<String>> solveNQueens(int n) {List<List<String>> res new ArrayList<>();return null;}void backtracking1(int n, int row, int[] columns) {// 是否在所有n行里都摆放好了皇后?if (row n) {count;// 找到了…...
Kubernetes(K8S)各种攻击方法
1. 准备工作 1.1. metarget使用 项目地址(教程):https://github.com/Metarget/metarget/blob/master/README-zh.md 注意:推荐在Ubuntu 18.04(推荐)安装。 1.1.1. 安装metarget git clone https://github.com/Metarget/metarget.git cd metarget/ sudo apt install pyt…...
【MySQL】内外连接
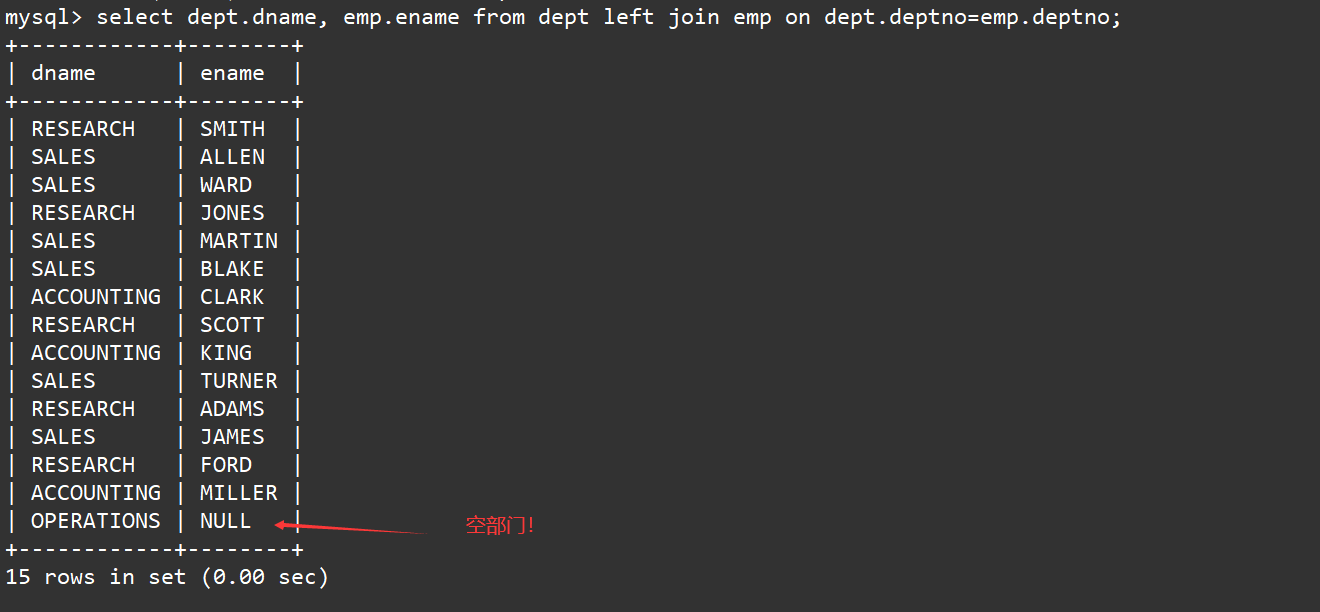
内外连接 一、内连接二、外连接1、左外连接2、右外连接 表的连接分为内连和外连。 一、内连接 内连接实际上就是利用where子句对两种表形成的笛卡儿积进行筛选。只不过为了让sql的可读性更好,我们使用其他的关键字进行内连接。 语法: SELECT ... FRO…...
selenium执行出现异常,SessionNotCreatedException ChromeDriver only supports
问题现状: 运行程序报错: selenium.common.exceptions.SessionNotCreatedException: Message: session not created: This version of ChromeDriver only supports Chrome version 114 Current browser version is 121.0.6167.85 with binary path /App…...

Flink:快速掌握批处理数据源的创建方法
Flink 社区最近 “基于FLIP-27” 设计了新的 Source 框架 。一些连接器(API)已迁移到这个新框架。本文介绍了如何使用这个新框架创建批处理源。 它是在为Cassandra实现Flink 批处理源时构建的。如果您有兴趣贡献或迁移连接器,这篇文章非常适合…...

基于cubeMX的正点原子miniSTM32对W25Q64的存储使用
一、实现目标 使用cubeMX建立项目工程,结合正点原子提供的hal库对W25Q64闪存调用的例程,实现W25Q64的读写。 二、实现过程 1、首先建立cubeMX工程,其他项设置不再叙述,只看连接W25Q64的SPI设置,这里使用SPI1…...
)
C++笔记(三)
封装意义: 在设计类的时候,属性和行为写在一起,表现事物 类在设计时,可以把属性和行为放在不同的权限下,加以控制。 访问权限有三种: public 公共 类内 类外都可以访问, protected保护 类内可以访问…...

c语言不定参数
时间记录:2024/1/22 一、不定参数的函数定义和使用到的c函数 (1)定义 void fun1(参数类型 argName,...); 示例: void fun1(int count,...);(2)获取不定参数的值 #include <stdarg.h> //包含头文件…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
