代码随想录算法训练营第29天(回溯算法05 | * 491.递增子序列 * 46.全排列 * 47.全排列 II
回溯算法part05
- 491.递增子序列
- 解题思路
- 与` 90.子集II `不同的点
- 回溯三部曲
- 46.全排列
- 解题思路
- 遇到的难点
- 思考
- 47.全排列 II
- 解题思路
- 注意点
- 拓展
- 需要加深理解的点(需复习
- 小总结
491.递增子序列
本题和大家刚做过的
90.子集II非常像,但又很不一样,很容易掉坑里。
题目链接: 491.递增子序列
文章讲解: 491.递增子序列
视频讲解: 491.递增子序列
解题思路
在90.子集II中我们是通过排序,再加一个标记数组来达到去重的目的。
而本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
与90.子集II不同的点
- 不能排序
- 不能用之前的used[]数组,而要用set,且set不需要跟着回溯,只负责本层里面取了哪些元素
- 需要判断每个path中元素个数是否大于等于2
- 需要判断每个path是否是递增的
回溯三部曲
- 递归函数参数:
- 全局变量result和path
- startIndex
- 终止条件:
要遍历整个树,可以没有 - 单层遍历逻辑
- 去重逻辑
- 局部变量HashSet uset; 记录本层元素是否重复使用,新的一层uset都会重新定义(清空),所以要知道uset只负责本层!

// uset用数组实现 效率高一些
class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new LinkedList<>();public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums, 0);return result;}public void backTracking(int[] nums, int startIndex){if(path.size() >= 2){result.add(new ArrayList<>(path));}if(startIndex >= nums.length){ // 这个终止条件可以没有,因为我们要遍历整个树return;}int[] uset = new int[201];for(int i = startIndex; i <nums.length; i++){if(!path.isEmpty() && path.get(path.size() - 1) > nums[i] || uset[nums[i] + 100] == 1) continue; //注意是continue而不是breakuset[nums[i] + 100] = 1;path.add(nums[i]);backTracking(nums, i + 1);path.remove(path.size() - 1);}}
}
// // uset用set实现
class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new LinkedList<>();public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums, 0);return result;}public void backTracking(int[] nums, int startIndex){if(path.size() >= 2){result.add(new ArrayList<>(path));}if(startIndex >= nums.length){ // 这个终止条件可以没有,因为我们要遍历整个树return;}HashSet<Integer> uset = new HashSet<>();for(int i = startIndex; i <nums.length; i++){if(!path.isEmpty() && path.get(path.size() - 1) > nums[i] || uset.contains(nums[i])) continue; //注意是continue而不是breakuset.add(nums[i]);path.add(nums[i]);backTracking(nums, i + 1);path.removeLast();}}
}
46.全排列
本题重点感受一下,排列问题 与 组合问题,组合总和,子集问题的区别。 为什么排列问题不用 startIndex
题目链接: 46.全排列
文章讲解: 46.全排列
视频讲解: 46.全排列
解题思路
不需要i = startIndex控制for循环开始位置,每次从i = 0开始
需要判断当前元素是否已经取过
遇到的难点
如何不重复取自身元素:used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次
思考
这道题的used数组和之前题目中的used数组作用的不同
- 这道题的used数组:记录此时path里都有哪些元素使用了
- 之前题目中的used数组:树层上对组合去重,一般要先将数组排序

// 解法1:通过判断path中是否存在数字,排除已经选择的数字
// 感觉这种比解法2好理解
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> permute(int[] nums) {if (nums.length == 0) return result;backtrack(nums, path);return result;}public void backtrack(int[] nums, LinkedList<Integer> path) {if (path.size() == nums.length) {result.add(new ArrayList<>(path));}for (int i =0; i < nums.length; i++) {// 如果path中已有,则跳过if (path.contains(nums[i])) {continue;} path.add(nums[i]);backtrack(nums, path);path.removeLast();}}
}
// 法2:通过used判断是否path中已取过当前数字
class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new LinkedList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {used = new boolean[nums.length];backTracking(nums);return result;}public void backTracking(int[] nums){if(path.size() == nums.length){result.add(new ArrayList<>(path));}for(int i = 0; i < nums.length; i++){if(used[i]){continue;}used[i] = true;path.add(nums[i]);backTracking(nums);used[i] = false;path.removeLast();}}
}
47.全排列 II
本题 就是我们讲过的
40.组合总和II去重逻辑 和46.全排列的结合,可以先自己做一下,然后重点看一下 文章中 我讲的拓展内容。 used[i - 1] == true 也行,used[i - 1] == false 也行
题目链接: 47.全排列 II
文章讲解: 47.全排列 II
视频讲解: 47.全排列 II
解题思路
40.组合总和II去重逻辑 和46.全排列的结合
注意点
nums数组排序
Arrays.sort(nums);
树层去重
if(i > 0 && nums[i - 1] == nums[i] && used[i - 1] == false) continue; // 树层去重
取过的元素不再重复取
if(used[i] == true) continue; // 取过的数标记为1
拓展
去重代码中,如果改成 used[i - 1] == true, 也是正确的!
这是为什么呢,就是上面我刚说的,如果要对树层中前一位去重,就用used[i - 1] == false,如果要对树枝前一位去重用used[i - 1] == true。
对于排列问题,树层上去重和树枝上去重,都是可以的,但是树层上去重效率更高!
树枝去重图例

需要加深理解的点(需复习
- 树层去重和树枝去重
- used数组在不同题中的作用
- 为什么这道题的used数组需要作为参数参与递归结合
40.组合总和II和90.子集II进行思考 491.递增子序列中的uset

小总结
491.递增子序列 不能用之前的used[]数组,而要用set,且set不需要跟着回溯,只负责本层里面取了哪些元素 used数组不需要回溯,不需要放在递归参数里面
46.全排列 used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次 used数组要回溯,要放在递归参数里面
47.全排列 II used数组:去重+取过的元素不再重复取 used数组要回溯,要放在递归参数里面
class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new LinkedList<>();boolean[] used;public List<List<Integer>> permuteUnique(int[] nums) {used = new boolean[nums.length];Arrays.sort(nums);backTracking(nums, used);return result;}public void backTracking(int[] nums, boolean[] used){if(path.size() == nums.length){result.add(new ArrayList<>(path));return;}for (int i =0; i < nums.length; i++) {// 树层去重if(i > 0 && nums[i - 1] == nums[i] && used[i - 1] == false) continue; // 树层去重if(used[i] == true) continue; // 取过的数标记为1used[i] = true;path.add(nums[i]);backTracking(nums, used);used[i] = false;path.removeLast();}}
}
相关文章:

代码随想录算法训练营第29天(回溯算法05 | * 491.递增子序列 * 46.全排列 * 47.全排列 II
回溯算法part05 491.递增子序列解题思路与 90.子集II 不同的点回溯三部曲 46.全排列解题思路遇到的难点思考 47.全排列 II解题思路注意点拓展需要加深理解的点(需复习 小总结 491.递增子序列 本题和大家刚做过的90.子集II非常像,但又很不一样,…...
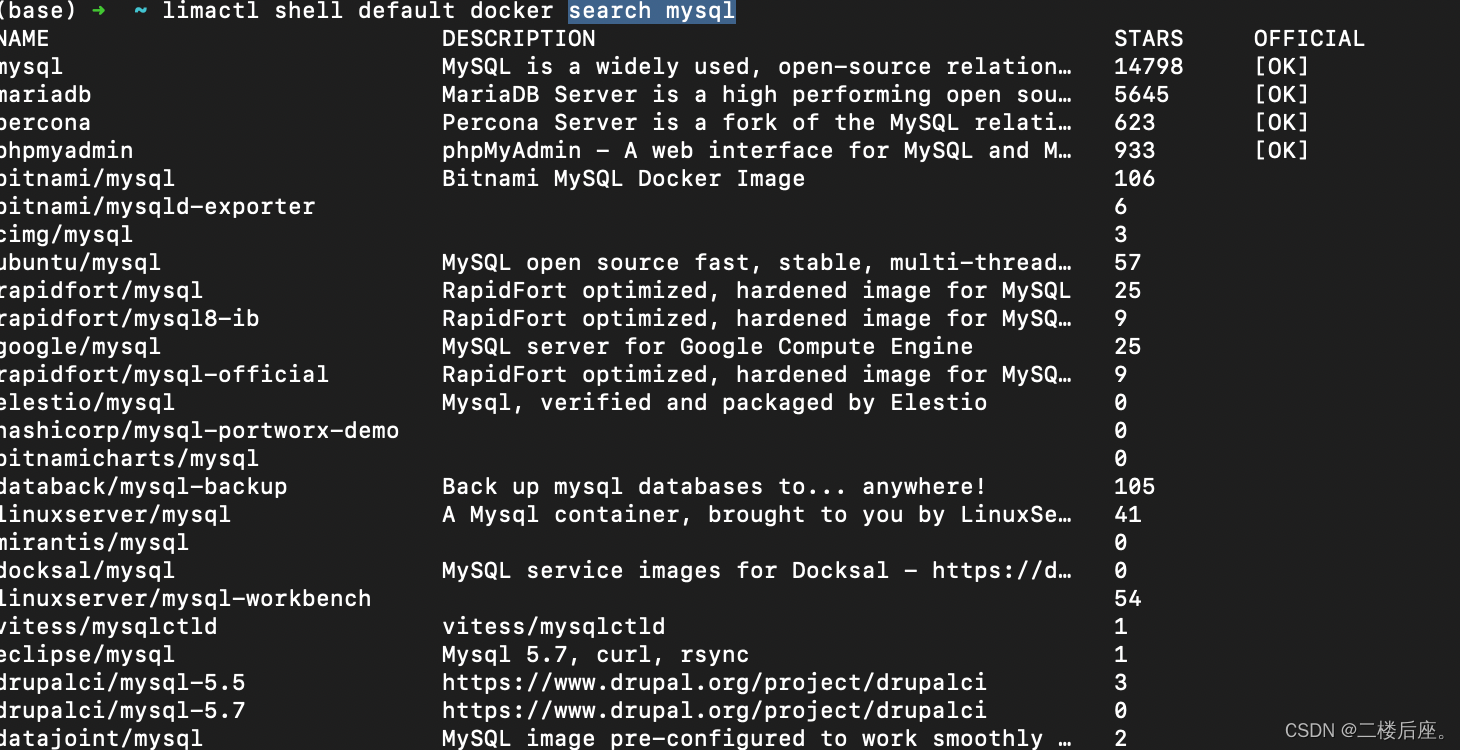
mac docker desktop被禁用了,如何使用虚拟机lima运行docker
安装lima brew install lima创建配置 echo "\\ndynamic:\n big-sur:\n image: docker://docker:git\n linux:\n image: docker.io/limasoftware/ubuntu:20.04 \\n" > ~/.lima/default.yaml启动名叫default的虚拟机 limactl start default测试 limactl …...
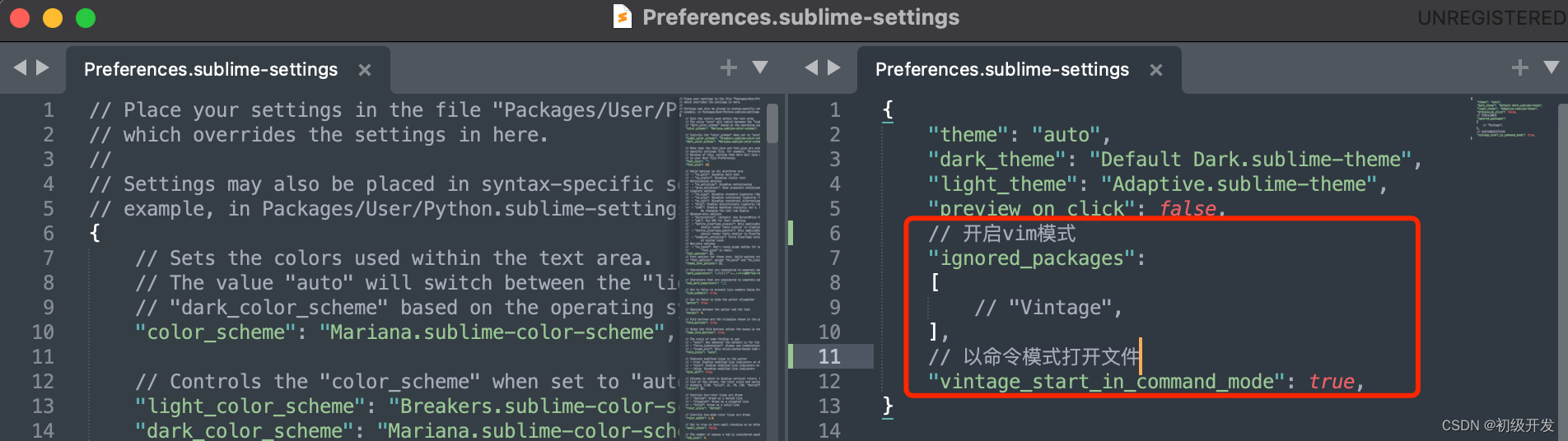
sublime text 开启vim模式
sublime text 开启vim模式 打开配置文件 mac下点击菜单栏 Sublime Text -> Settings... -> Settings 修改配置文件并保存 添加配置 // 开启vim模式 "ignored_packages": [// "Vintage", ], // 以命令模式打开文件 "vintage_start_in_comman…...

JS词法结构
编程语言的词法结构是一套基础性规则,用来描述如何使用这门语言来编写程序。作为语法的基础,它规定了诸如变量名是什么样的、怎么写注释,以及程序语句之间如何分隔等规则。 2.1程序的文本 JS区分大小写 JS忽略程序记号(token&am…...

程序媛的mac修炼手册-- 如何用Python节省WPS会员费
上篇分享了如何用微博爬虫,咱举例爬了女明星江疏影的微博数据。今天就用这些数据,给大家安利一下怎么用Python实现WPS中部分Excel付费功能。 MacOS系统自带的工具,绝大多数都非常顶,除Numbers外。当然,page比起word来&…...
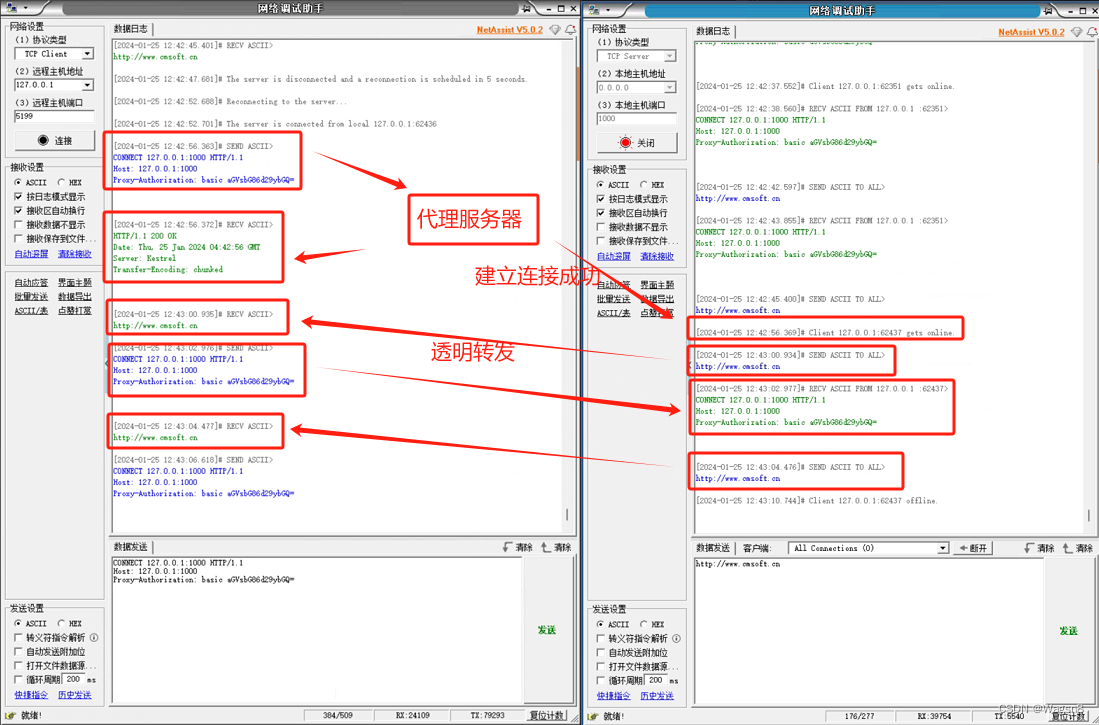
ASP.NET Core NE8实现HTTP Upgrade和HTTP CONNECT代理服务器
看到一个文章[Go] 不到 100 行代码实现一个支持 CONNECT 动词的 HTTP 服务器 在NET8中如何实现 创建项目为MiniApi 编辑Program.cs文件。 var builder WebApplication.CreateSlimBuilder(args);var app builder.Build();// 将HTTP请求通过协议升级机制转为远程TCP请求&…...

apipost和curl收不到服务器响应的HTTP/1.1 404 Not Found
windows的apipost发送请求后,服务器响应了HTTP/1.1 404 Not Found,但是apipost一直显示发送中。 linux上的curl也一样。 使用wireshark抓包发现收到了响应,但是wireshark识别不了(图中是回应404后关闭了连接)ÿ…...

javascript:计算一个坐标数组的最小值点、最大值点、中心点
作者:CSDN _乐多_ 本文将介绍使用 javascript 语言计算一个坐标数组的最小值点、最大值点、中心点的代码。 文章目录 一、代码 一、代码 function calculateCenterPoint(points) {if (points.length 0) {return null;}let sumX 0;let sumY 0;let sumZ 0;for …...

使用远程工具连接Linux系统——使用Root用户登录
1、启动虚拟机,输入以下命令 进入root用户 sudo su或 su root修改ssh配置文件 vim /etc/ssh/sshd_config找到PermitRootLogin 并用#注释掉当前行 # PermitRootLogin prohibit-password添加: PermitRootLogin yes键入esc输入:wq保存退出 2、重启服…...
JuiceSSH结合内网穿透实现移动端设备公网远程访问Linux虚拟机
文章目录 1. Linux安装cpolar2. 创建公网SSH连接地址3. JuiceSSH公网远程连接4. 固定连接SSH公网地址5. SSH固定地址连接测试 处于内网的虚拟机如何被外网访问呢?如何手机就能访问虚拟机呢? cpolarJuiceSSH 实现手机端远程连接Linux虚拟机(内网穿透,手机端连接Linux虚拟机) …...

06-枚举和模式匹配
上一篇:05-使用结构体构建相关数据 在本章中,我们将介绍枚举。枚举允许你通过枚举其可能的变体来定义一种类型。首先,我们将定义并使用一个枚举,以展示枚举如何与数据一起编码意义。接下来,我们将探索一个特别有用的枚…...

【C/C++】C/C++编程——C++ 开发环境搭建
C的开发环境种类繁多,以下是一些常见的C 集成开发环境: AppCode :构建与JetBrains’ IntelliJ IDEA 平台上的用于Objective-C,C,C,Java和Java开发的集成开发环境CLion:来自JetBrains的跨平台的C/C的集成开…...

Go 接口
接口概览 接口大概理解 接口类型是队其他类型行为的概括与抽象 接口类型中,包含函数声明,但没有数据变量接口的作用通过使用接口,可以写出更加灵活和通用的函数,这些函数不用绑定在一个特定的类型实现上Go 接口特征 很多面向对象…...
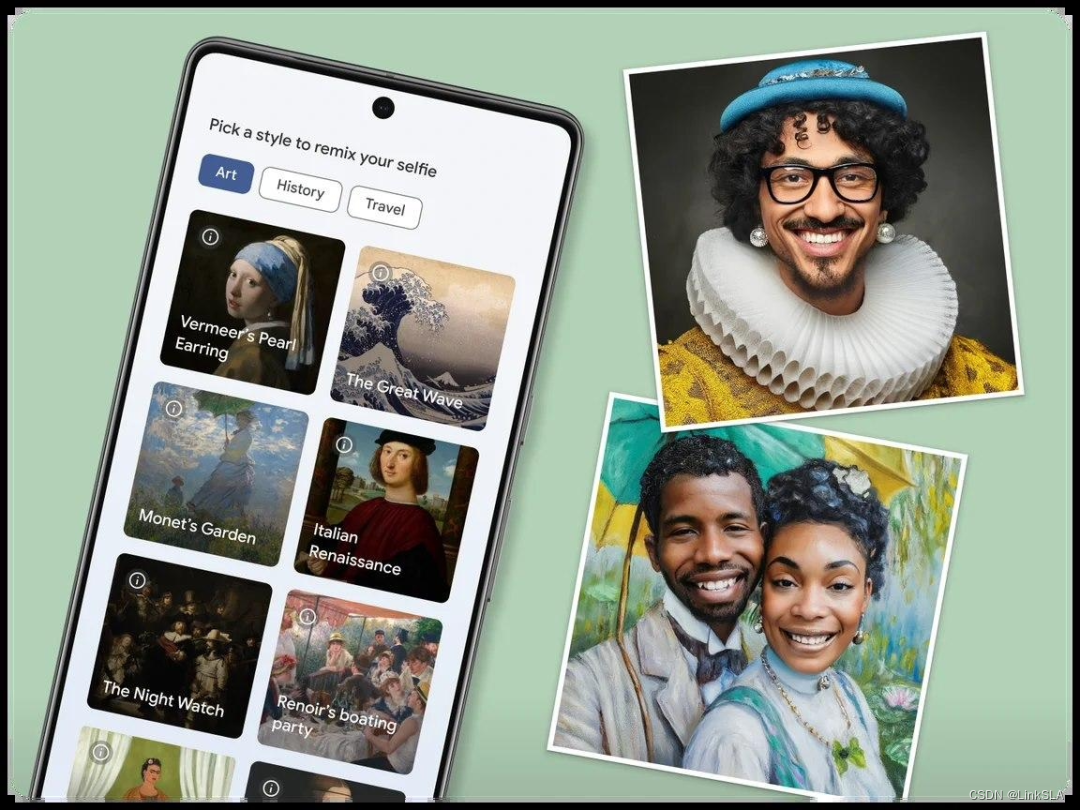
用 AI 将自拍照 P 进不同艺术作品,谷歌发布「艺术自拍 2」
1 月 24 日消息,谷歌旗下「艺术与文化」应用今日宣布,2018 年推出的「艺术自拍」功能在时隔近六年后,借助生成式 AI 的力量回归。官方表示,「艺术自拍 2」将再次使用户与艺术面对面,重新探访世界各地的艺术、历史和文化…...
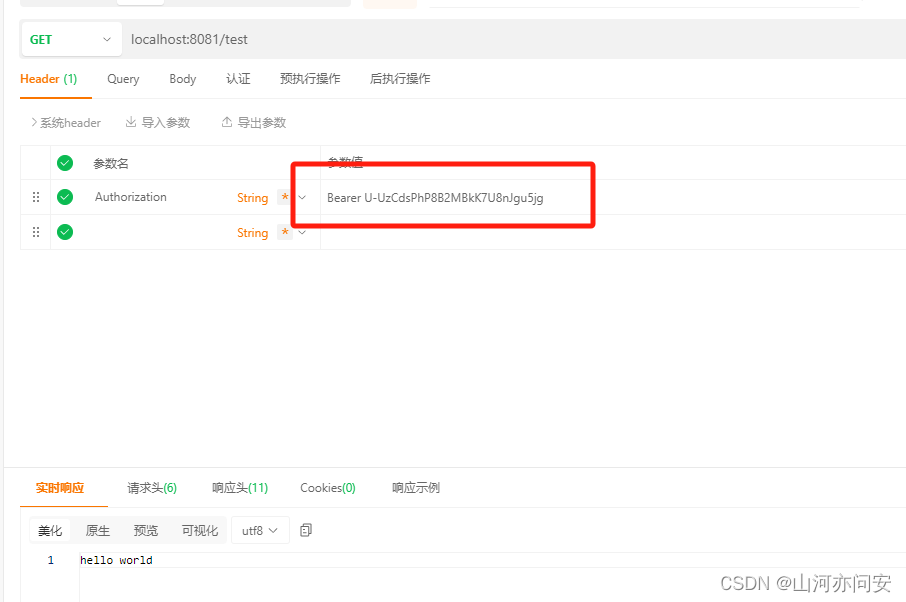
SpringSecurity+OAuth2.0 搭建认证中心和资源服务中心
目录 1. OAuth2.0 简介 2. 代码搭建 2.1 认证中心(8080端口) 2.2 资源服务中心(8081端口) 3. 测试结果 1. OAuth2.0 简介 OAuth 2.0(开放授权 2.0)是一个开放标准,用于授权第三方应用程序…...

c# 策略模式
在 C# 中,策略模式是一种行为型设计模式,它定义了一系列算法,并将每个算法封装到具有公共接口的独立类中,使得它们可以互相替换。这样可以使得算法的选择独立于算法的使用者,从而提高了灵活性和可维护性。 以下是策略…...

消息队列RabbitMQ.03.死信交换机的讲解与使用
目录 一、死信队列(延迟队列) 概念讲解 二、确认消息(局部方法处理消息) 三、代码实战 1.编写生产者代码,配置消息、直连交换机、路由键 1.1代码解析: 2.配置消费者接受类接受直连交换机的路由键 2.1. String msgÿ…...
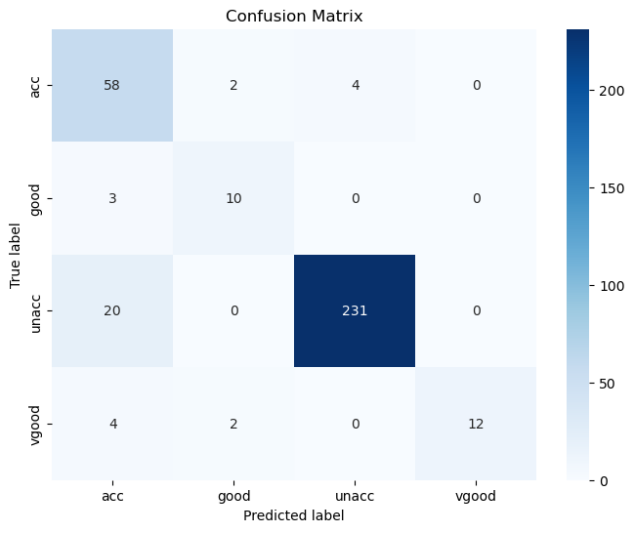
人工智能原理实验4(2)——贝叶斯、决策求解汽车评估数据集
🧡🧡实验内容🧡🧡 汽车数据集 车子具有 buying,maint,doors,persons,lug_boot and safety六种属性,而车子的好坏分为uncc,ucc,good and vgood四种。 🧡🧡贝叶斯求解🧡🧡…...

算力网络:未来计算资源的驱动力
文章目录 前言一、算力网络的基本概况(一)算力网络的基本概念(二)算力网络研究进展二、运营商的算力网络架构(一)算力网络基础设施构成(二)算力网络编排管理(三)能力开放三、算力网络的优势(一)弹性计算(二)降低成本(三)去中心化四、算力网络的应用场景(一)人…...

java动态导入excel按照表头生成数据库表
1、创建接口接收文件 //controller层 PostMapping("/importExcel1")public void importExcel1(HttpServletRequest request, MultipartFile file) {try {waterMeterService.importExcel1(request,file);} catch (Exception e) {throw new RuntimeException(e);}}//se…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
