手撕重采样,考虑C的实现方式
一、参考文章:
重采样、上采样、下采样 - 知乎 (zhihu.com)
先直接给结论,正常重采样过程如下:
1、对于原采样率fs,需要重采样到fs1,一般fs和fs1都是整数哈,则先找fs和fs1的最小公倍数,设为m,设m/fs=M,m/fs1 = L。则信号先要做M倍的插值,即上采样,再做1/L倍的抽取,即下采样;
2、因为插值和抽取,信号的频带都会变,也就是信号会引入噪声,所以需要滤波处理;
3、具体来说,插值,频谱变窄,即信号频带压缩了,如果不做处理,信号会包含带宽以外的噪声,所以需要做低通只滤出变窄的信号频带,去掉噪声。抽取,之后的频谱会变宽,即最终和原信号频谱对不上,所以又需要低通滤波,将信号滤到和原信号一样的频带。
4、具体来说,第一个低通的通带(归一化)是0~1/M,第二个低通的通带是0~1/L。找到满足性能的滤波器,还是比较有考验的。
回到程序,上文中第一段,涉及到滤波器,改用0相位滤波,即调用matlab的filtfilt。滤波时考虑使用原程序中的滤波器幅值归一化。且,加入抽取、滤波,即实现重采样完整流程,最后,还对比matlab自己的resample函数结果。如下:
clc;
close all;
clear all;
%%%%%%%%%%%%%%%%%程序说明
% 1、使用'zero stuffing'和'low pass filter'实现内插/上采样N = 4; % 上采样率
h_t = ones(1, N);
h_t_lp = sinc(-pi:2*pi/20:pi);
% h_t_lp = h_t_lp ./ sum(h_t_lp); % 归一化LPFA = 1.5;
B = 1;
f1 = 50;
f2 = 100;
Fs = 1000;
t = 0:1/Fs:1;
sig = A * cos(2 * pi *f1 * t) + B * sin(2 * pi *f2 * t); % 原始数据% 插值:插入0
sig_zerostuff = zeros(1, length(sig) * N);
sig_zerostuff(1 : N : length(sig_zerostuff)) = sig;
sig_zerostuff_lp = conv(sig_zerostuff, h_t_lp);
% 采样保持:使得插入的数值与原数据的数值一致
sig_sample_hold = conv(sig_zerostuff, h_t);
% 将采样保持的信号经过LPF
h_t_lp = h_t_lp ./ sum(h_t_lp); % 归一化LPF
% sig_sample_hold_lp = conv(sig_sample_hold, h_t_lp);
sig_sample_hold_lp = filtfilt(h_t_lp,1,sig_sample_hold);subplot(5,1,1);
stem(sig,'MarkerFaceColor',[0 0 1]);xlim([1 25]);
title('原始数据');subplot(5,1,2);
stem(sig_zerostuff,'MarkerFaceColor',[1 0 0]);xlim([1 25*N]);
title('插值后的数据');subplot(5,1,3);
stem(sig_zerostuff_lp,'MarkerFaceColor',[1 0 0]);xlim([1 25*N]);
title('插值后的数据通过LPF');subplot(5,1,4);
stem(sig_sample_hold,'MarkerFaceColor',[1 0 0]);xlim([1 25*N]);
title('插值保持后的数据');subplot(5,1,5);
stem(sig_sample_hold_lp,'MarkerFaceColor',[1 0 0]);xlim([1 25*N]);
title('采样保持的数据通过LPF');% 抽取,1/3
sig_sample_hold_lp_downsample = sig_sample_hold_lp(1:3:end);
% sig_sample_hold_lp_downsample_lp = conv(sig_sample_hold_lp_downsample, h_t_lp);
sig_sample_hold_lp_downsample_lp = filtfilt(h_t_lp,1,sig_sample_hold_lp_downsample);
sig_resample = resample(sig, 4, 3);figure
subplot(4,1,1);
stem(sig,'MarkerFaceColor',[0 0 1]);xlim([1 120]);
title('原始数据');
subplot(4,1,2);
stem(sig_sample_hold_lp_downsample,'MarkerFaceColor',[0 1 0]);xlim([1 120]);
title('抽取数据');
subplot(4,1,3);
stem(sig_sample_hold_lp_downsample_lp,'MarkerFaceColor',[1 0 0]);xlim([1 120]);
title('抽取数据通过LPF');
subplot(4,1,4);
stem(sig_resample,'MarkerFaceColor',[0 0 0]);xlim([1 120]);
title('resample重采样数据');
结果:


还是文章一,插值可以用另一种方法,即,不是插0值或者保持,而是用其他插值法,matlab有interp函数,可以设置参数用不同插值法。典型的线性插值,应该比较好找C代码。
先看看文章的效果:
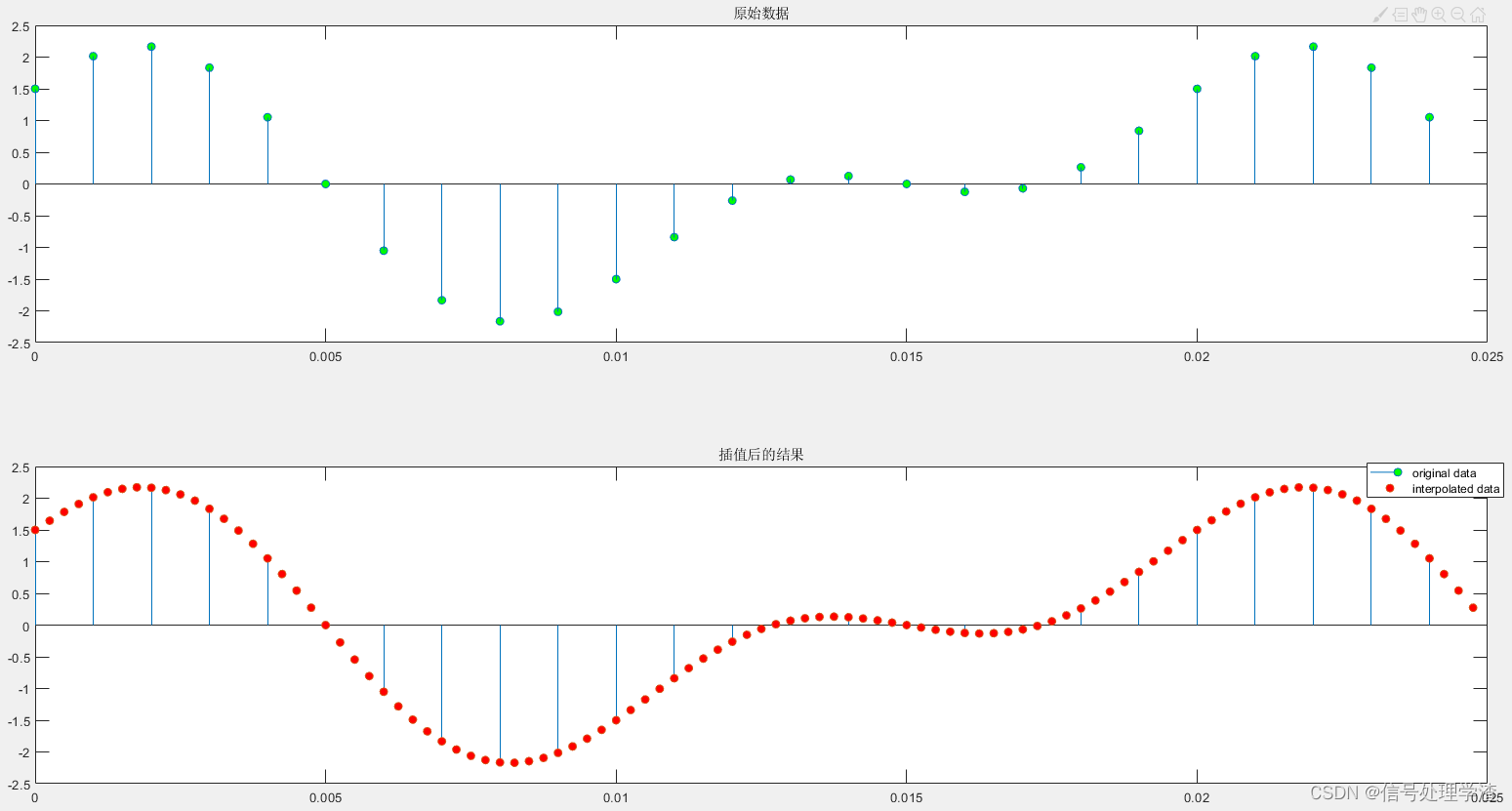 效果还是可以的。
效果还是可以的。
关于线性插值C代码,时间关系暂未验证哈:
线性插值_c语言实现_线性插值c语言程序-CSDN博客
标准C语言插值函数 - 百度文库 (baidu.com)
二、一种自创的简单、近似算法
应该有很多这样使用的,只是介绍的少,属于私下处理算法。
简单来说,思路是:
考查原始信号时间点和重采样后信号的时间点,一般来说,重采样信号的一个时间点,是处在原始信号的两个信号点之间(若重合,则直接不用计算),根据此时间点到原信号两个信号点的距离,用原信号这两个信号点插值得到重采样信号此点的信号幅值。
所以很明显,这种方法的优点是,不用考虑抽取、插值、滤波这些麻烦事,只考虑插值即可。
但是,缺点也有,就是不能统一处理,必须每个点都分别处理。
时间关系,后续,可以再测试下。
三、查到一个专利,但是算法还是有问题,未程序实现:
CN202010258902一种数字信号的任意重采样方法及系统
无法添加附件,是个问题。
主要步骤有:


简单说是用sinc函数实现。但是还有较多看不懂的。感觉不理解0052到0058的用意是啥。但是貌似,可以不管其他,直接用最后一个公式算就行了......
后续试试程序仿真...
有关sinc函数(也较辛格函数):20211003:数字滤波器前置知识,sinc函数与Sa函数_sinc函数与sa函数区别-CSDN博客
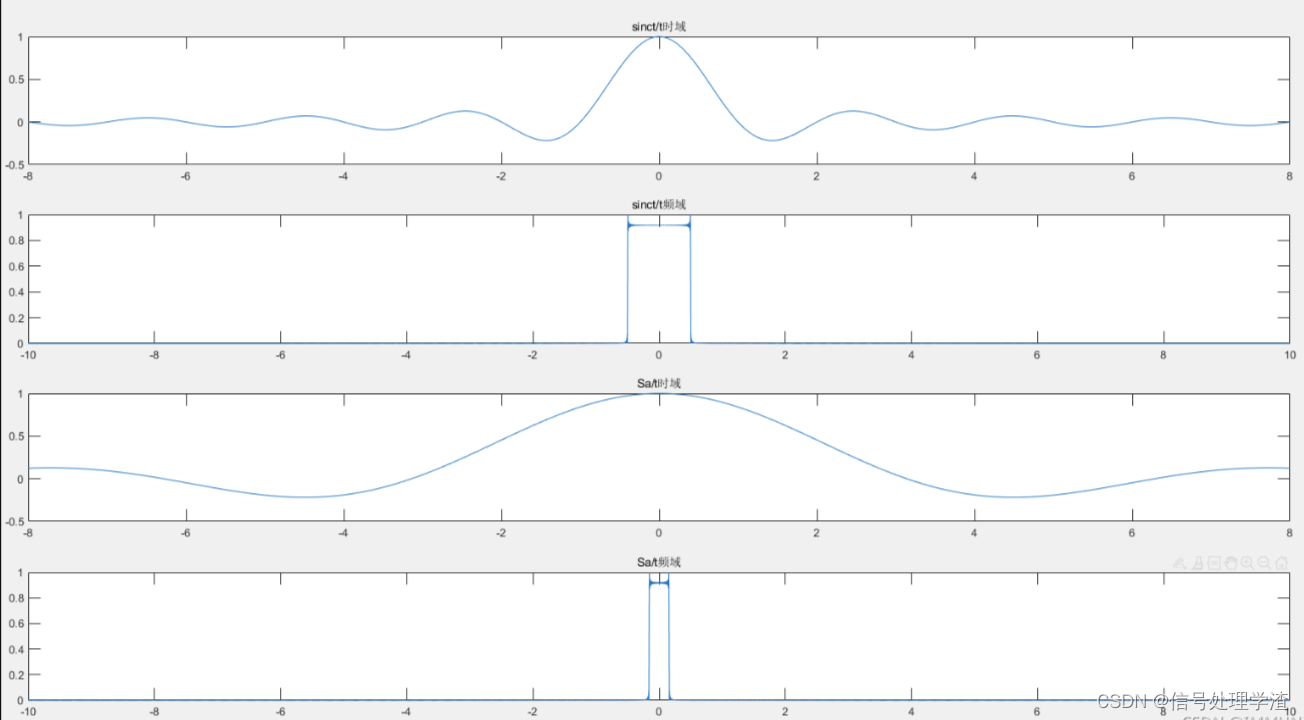
程序仿真来了,但是结果好像不对,不知道是这理论有问题还是哪里理解不对,欢迎交流了:
clc; clear all; close all;A = 1.5;
B = 1;
f1 = 50;
f2 = 100;
Fs = 1000;
t = 0:1/Fs:1;
sig = A * cos(2 * pi *f1 * t) + B * sin(2 * pi *f2 * t); % 原始数据M = 4; % 上采样率
N = 3; % Fs1/Fs = M/N
INF_L = 50;N1 = length(sig);
N2 = floor(N1*M/N);
sig_out = zeros(1,N2);for m=1:N2if(m==800)m=800;endseq_begin = floor(M*m/N) - INF_L + 1;if(seq_begin<1)seq_begin=1;endseq_end = floor(M*m/N) + INF_L;if(seq_end>N1)seq_end=N1;endfor n=seq_begin:seq_endtmp = abs(M*m - N*n)+1;sig_out(m) = sig_out(m) + sig(n)*sin(pi*tmp/M)./(pi*tmp/M);end
endsig_out2 = resample(sig,4,3);
subplot(3,1,1);
stem(sig,'MarkerFaceColor',[1 0 0]);xlim([1 100]);
title('原数据');subplot(3,1,2);
stem(sig_out,'MarkerFaceColor',[1 1 0]);xlim([1 100]);
title('sinc重采样数据');subplot(3,1,3);
stem(sig_out2,'MarkerFaceColor',[1 0 1]);xlim([1 100]);
title('resample重采样数据');zhh = 1;结果:

相关文章:

手撕重采样,考虑C的实现方式
一、参考文章: 重采样、上采样、下采样 - 知乎 (zhihu.com) 先直接给结论,正常重采样过程如下: 1、对于原采样率fs,需要重采样到fs1,一般fs和fs1都是整数哈,则先找fs和fs1的最小公倍数,设为m…...

网络安全产品之认识入侵防御系统
由于网络安全威胁的不断演变和增长。随着网络技术的不断发展和普及,网络攻击的种类和数量也在不断增加,给企业和个人带来了巨大的安全风险。传统的防火墙、入侵检测防护体系等安全产品在面对这些威胁时,存在一定的局限性和不足,无…...

第20课 在Android Native开发中加入新的C++类
这节课我们开始利用ffmpeg和opencv在Android环境下来实现一个rtmp播放器,与第2课在PC端实现播放器的思路类似,只不过在处理音视频显示和播放的细节略有不同。 1.压缩备份上节课工程文件夹并修改工程文件夹为demo20,将demo20导入到Eclipse或…...
)
python学习笔记11(程序跳转语句、空语句)
(一)程序跳转语句 1、break 用法:循环语句中使用,结束本层循环,一般搭配if来使用。注意while/else语法 示例: i0; while i<3:user_nameinput(请输入用户名:)pwdinput("请输入密码&a…...

C. Doremy‘s City Construction(二分图问题)
思路:把集合划分成两部分,一部分中每个数都比另一部分小,这两部分连成一个完全二分图,这种情况是最优的,还需要特判所有数都相等的情况. 代码: void solve(){int n;cin >> n;vector<int>a(n 1);for(int i 1;i < n;i )cin >> a[…...

PHP“引用”漏洞
今日例题: <?php highlight_file(__FILE__); error_reporting(0); include("flag.php"); class just4fun { var $enter; var $secret; } if (isset($_GET[pass])) { $pass $_GET[pass]; $passstr_replace(*,\*,$pass); } $o unser…...

计算机网络-AAA原理概述
对于任何网络,用户管理都是最基本的安全管理要求之一,在华为设备管理中通过AAA框架进行认证、授权、计费实现安全验证。 一、AAA概述 AAA(Authentication(认证), Authorization(授权), and Accounting(计费))是一种管理框架&#…...
Oracle BIEE 示例(一)数据透视表2
1 背景 版本:BIEE 12C 视图:数据透视表 实现内容(顺序与具体内容不一致): 2 空列显示(方法一) 2.1 问题 列为空时,标题栏不显示信息。 2.2 期望 即使数据为空,也要显示列名。 2.3 官方资料 2.3.1 操作步骤 2.3.1.1 要在分析级别关闭空值隐藏,请执行以下操作…...
)
算法训练营Day50(动态规划11)
说明 较难,二刷再仔细打代码 123.买卖股票的最佳时机III 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 提醒 这道题一下子就难度上来了,关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次&a…...
DS:顺序表的实现(超详细!!)
创作不易,友友们给个三连呗! 本文为博主在DS学习阶段的第一篇博客,所以会介绍一下数据结构,并在最后学习对顺序表的实现,在友友们学习数据结构之前,一定要对三个部分的知识——指针、结构体、动态内存管理的…...

用flinkcdc debezium来捕获数据库的删除内容
我在用flinkcdc把数据从sqlserver写到doris 正常情况下sqlserver有删除数据,doris是能捕获到并很快同步删除的。 但是我现在情况是doris做为数仓,数据写到ods,ods的数据还会通过flink计算后写入dwd层,所以此时ods的数据是删除了…...

mariadb数据库从入门到精通
mariadb数据库的安装以及安全初始化 mariadb数据库的安装以及安全初始化 mariadb数据库的安装以及安全初始化一、实验前提二、mariadb数据库的安装三、mariadb数据库安全初始化3.1 设定数据库基本的安全初始化3.2关闭对外开放端口 系列文章目录一、查看数据库二、进入库并且查看…...
LabVIEW探测器CAN总线系统
介绍了一个基于FPGA和LabVIEW的CAN总线通信系统,该系统专为与各单机进行系统联调测试而设计。通过设计FPGA的CAN总线功能模块和USB功能模块,以及利用LabVIEW开发的上位机程序,系统成功实现了CAN总线信息的收发、存储、解析及显示功能。测试结…...
)
侧输出流(Side Output)
侧输出流(Side Output)是处理函数中的一个重要功能,允许我们将自定义的数据发送到侧输出流中进行处理或输出。通过将数据发送到侧输出流,我们可以将不同的数据流进行分离,以便进行不同的处理和操作。 在处理函数中&…...

Vue 动态组件与异步组件:深入理解与全面应用
聚沙成塔每天进步一点点 本文内容 ⭐ 专栏简介1. 动态组件实现原理:用法示例: 2. 异步组件实现原理:用法示例: 3. 异步组件的高级应用a. 异步组件的命名:b. 异步组件的加载状态管理: ⭐ 写在最后 ⭐ 专栏简…...
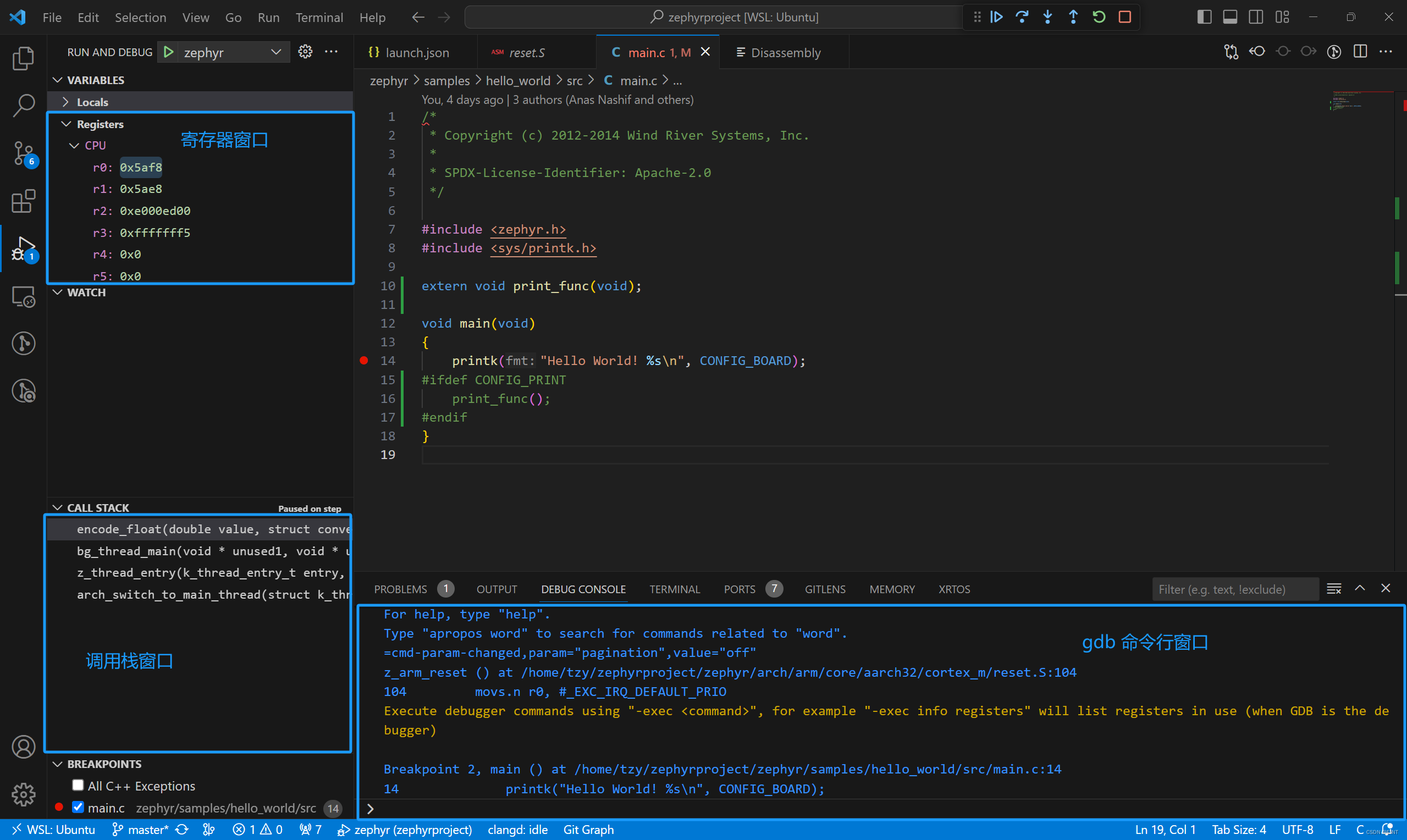
Zephyr 源码调试
背景 调试环境对于学习源码非常重要,但嵌入式系统的调试环境搭建稍微有点复杂,需要的条件略多。本文章介绍如何在 Zephyr 提供的 qemu 上调试 Zephyr 源码,为后续分析 Zephyr OS 相关原理做铺垫。 环境 我的开发环境为 wsl ubuntu…...

数学建模绘图
注意:本文章旨在记录观看B站UP数模加油站之后的笔记文章,无任何商业用途~~ 必备网站 以下网站我都试过,可以正常访问 配色(取色)网站: Color Palettes Generator and Color Gradient Tool Python&#x…...

代码随想录算法训练营第十天 | 239.滑动窗口最大值、347.前K个高频元素
代码随想录算法训练营第十天 | 239.滑动窗口最大值、347.前K个高频元素 文章目录 代码随想录算法训练营第十天 | 239.滑动窗口最大值、347.前K个高频元素1 LeetCode 239.滑动窗口最大值2 LeetCode 347.前K个高频元素 1 LeetCode 239.滑动窗口最大值 题目链接:https…...

【Godot4自学手册】第五节用GDScript语言让主人公动起来
GDScript 是Godot自带的编程语言,用于编写游戏逻辑,它是一种高级面向对象的指令式编程语言,使用渐进类型,专为 Godot 构建。在这一小节里,我将自学用GDScript语言控制主人公的行走和攻击。 一、给Player节点添加GDScr…...

被问到Tomcat是什么该怎么回答?他还有一个好帮手JDK你知道吗?
目录 Tomcat简介: 使用建议: Tomcat好帮手---JDK Tomcat和JDK的关系 安装JDK 1.打开浏览器输入网址 Oracle | Cloud Applications and Cloud Platform 进入Oracle官网 2、在官网首页菜单栏,点击产品,在硬件和软件中找到Java࿰…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
