算法优化:LeetCode第122场双周赛解题策略与技巧
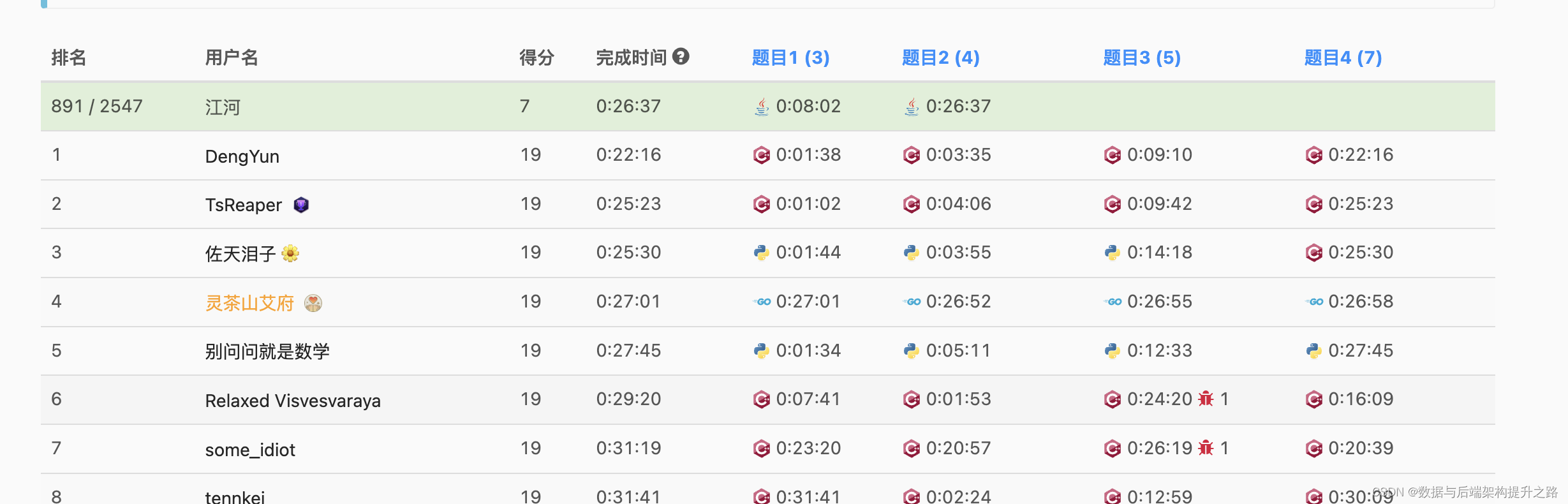
接下来会以刷常规题为主 ,周赛的难题想要独立做出来还是有一定难度的,需要消耗大量时间
比赛地址
3011. 判断一个数组是否可以变为有序
public class Solution {public int minimumCost(int[] nums) {if (nums.length < 3) {// 数组长度小于3时,无法分割成3个子数组return -1;}int minCost = Integer.MAX_VALUE;int n = nums.length;// 第一个分割点至少在索引1,第二个分割点至少在索引2for (int i = 1; i < n - 1; i++) {for (int j = i + 1; j < n; j++) {int cost = nums[0] + nums[i] + nums[j];minCost = Math.min(minCost, cost);}}return minCost;}
}100164. 通过操作使数组长度最小
冒泡排序
class Solution {public boolean canSortArray(int[] nums) {int n = nums.length;for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (Integer.bitCount(nums[j]) == Integer.bitCount(nums[j + 1]) && nums[j]>nums[j + 1]) {// 如果前一个元素的1的数量大于后一个元素的1的数量,交换它们int temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;}}}// 遍历完后,检查数组是否有序for (int i = 0; i < n - 1; i++) {if (nums[i] > nums[i + 1]) {return false;}}return true;}
}100181. 将数组分成最小总代价的子数组 I
当 x<y 时,x mod y=x 因此如果选择数组中的两个不相等的元素,则可以删除较大元素,保留较小元素。
用 minNum表示数组 nums 中的最小元素
用 minCount 表示数组 nums 中的 minNum 的出现次数
分别考虑 minCount=1 和 minCount>1 的情况。
- 如果 minCount=1
则可以每次选择 minNum 和另一个元素,由于 minNum 一定小于另一个元素,因此总是可以删除另一个元素,保留 minNum,直到数组 nums 中只有一个元素 minNum,数组 nums的最小长度是 1。
- 如果 minCount>1
- 如果数组 nums 中存在一个元素 num 满足 num mod minNum≠0 ,记 newNum= (num mod minNu)
- 则必有 0<newNum<minNum 可以在一次操作中选择 num 和 minNum ,删除这两个元素并添加元素newNum。
- 由于 newNum < minNum ,因此 newNum 成为数组 nums 中的新的最小元素且最小元素唯一,之后可以每次选择 newNum 和另一个元素,其效果是删除另一个元素,保留 newNum ,直到数组 nums 中只有一个元素 newNum ,数组 nums 的最小长度是 1
- 如果数组 nums 中不存在元素 num 满足 num mod minNum ≠ 0 ,则无法通过操作得到小于 minNum 的元素,因此在将所有大于 minNu 的元素删除之后,剩余 minCount 个元素 minNum 。由于每次可以选择 2 个元素 minNum 执行操作得到元素 0 无法继续操作,因此 minCount 个元素 minNum 的最多操作次数可以根据count_min的奇偶性判断
class Solution:def minimumArrayLength(self, nums: List[int]) -> int:min_val = min(nums)count_min = nums.count(min_val)for num in nums:if num % min_val != 0:return 1 # 产生了新的更小值# 没有产生新的最小值,计算最小值的数量return (count_min ) // 2 +1 if count_min % 2 != 0 else count_min // 2100178. 将数组分成最小总代价的子数组 II
一、直接用滑动窗口求解
这种方法会超时
class Solution:def minimumCost(self, nums: List[int], k: int, dist: int) -> int:first = nums[0] # 初始元素的代价window_size = dist + 1 # 窗口大小minimumCost = float('inf') # 初始化最小代价为无穷大# 遍历数组,寻找除第一个和最后一个元素之外的最小的 k-1 个元素for start in range(1, len(nums) - window_size + 1):window = nums[start:start + window_size]sorted_window = sorted(window)# 获取除第一个的 k-1 个最小元素的和window_cost = sum(sorted_window[:k-1])# 更新最小代价minimumCost = min(minimumCost, window_cost)# 最终的最小总代价是第一个元素的代价加上最小窗口代价return first + minimumCost 二、引入堆的代码实现
效率和之前的方法相差无几
class Solution:def minimumCost(self, nums: List[int], k: int, dist: int) -> int:first = nums[0]n = len(nums)minimumCost = float('inf')for start in range(1, n - dist):# 维护一个大小为 dist + 1 的最小堆min_heap = nums[start:start + dist + 1]heapq.heapify(min_heap)window_cost = 0# 弹出最小的 k-1 个元素并计算它们的和for _ in range(k-1):if min_heap:window_cost += heapq.heappop(min_heap)minimumCost = min(minimumCost, window_cost)return first + minimumCost三、大小顶堆、延迟删除、滑动窗口
这道题目的思路是利用滑动窗口结合两个堆(优先队列)来找出序列中指定数量(`k-1`)的最小数的和,它们是从序列的某个区间(该区间长度由`dist`决定)中选择出来的。这个序列中的第一个数 (`nums[0]`) 是固定的,所以总是被包含在结果中。
下面是详细的解题步骤:
-
初始化两个堆:一个小顶堆
small来保存当前窗口中的最小的k-2个数,以及一个大顶堆big来保存窗口内剩余的数。 -
使用 HashMap 进行延迟删除:为了实现有效地从堆中删除特定的非堆顶元素,创建两个
HashMap(smallMark和bigMark) 来标记堆中元素是否已经被 "删除"。该删除实际上是延迟执行的,即直到这个元素出现在堆顶时才真正被排除。 -
填充初始窗口:从
nums数组的第二个元素开始,将dist+1长度内的元素放入big堆。 -
从
big中取出k-2个最小元素:这k-2个元素是将要加入small的,记录这k-2个数的和作为窗口的当前总和。 -
滑动窗口:在数组中滑动窗口,并动态维护这两个堆以保持正确的最小
k-2个数的总和。 -
调整堆:当窗口滑动导致元素移出窗口时,更新
small堆以保持其有效性,并进行相应的调整。如果移出的元素当前在small中,则它需要被标记为已删除;如果它在big中,则直接标记为已删除。 -
处理新进入窗口的元素:窗口滑动时,可能会有新的元素进入。这些新元素需要加入到
big堆中。从big中取出的最小元素会放入small堆,并更新当前窗口总和(sum)。 -
求解最终结果:在滑动窗口过程中,每次窗口更新后,计算此时的窗口总和加上
nums[0](固定加入)。所有窗口中总和的最小值即为所求问题的答案。
class Solution {// small是小顶堆 维护前k-2小的数// big是大顶堆 维护窗口内剩下的数PriorityQueue<Integer> small, big;// 标记当前元素是否已经被删除以及被删除的个数HashMap<Integer, Integer> smallMark, bigMark;// samll和big当前未被删除的元素个数int smallSiz, bigSiz;long sum;public long minimumCost(int[] nums, int k, int dist) {// k个 除掉第一个 还要选k-1个// 枚举第2个 nums[i] nums[i+1]... nums[i+dist] 里选k-2个最小的数// nums[i+1] nums[i+k-2]small = new PriorityQueue<>(Collections.reverseOrder());smallSiz = 0;smallMark = new HashMap<>();big = new PriorityQueue<>();bigSiz = 0;bigMark = new HashMap<>();// 当前小顶堆的和 也就是前k-2小的和sum = 0;int n = nums.length;// 把nums[1+1]...nums[1+dist]里的数加入到big里for (int i = 2; i <= Math.min(n-1, dist+1); i++) {big.add(nums[i]);bigSiz++;}// 取出前k-2小的数放入smallfor (int i = 0; i < k-2; i++ ) {int tmp = big.poll();bigSiz--;sum += tmp;small.add(tmp);smallSiz++;}long res = nums[0] + nums[1] + sum;// 枚举第二个数的位置// 枚举的位置从i-1变成i时 nums[i]离开了窗口 nums[i+dist]进入了窗口for (int i = 2; i + k-2 < n; i++) {// 移除nums[i]// 因为要访问small.peek() 为了确保small.peek()是未被删除的元素 需要先更新smallupdateSmallPeek();// nums[i]在前k-2小里if (smallSiz > 0 && small.peek() >= nums[i]) {// 因为nums[i] 是可能小于small.peek()的 我们没法直接删除nums[i] 所以要标记一下smallMark.merge(nums[i], 1, Integer::sum);// 从small里删除nums[i]smallSiz--;sum -= nums[i];} else {// nums[i]不在前k-2小里 bigMark.merge(nums[i], 1, Integer::sum);bigSiz--;// 这里是为了使得small的数量变成k-3个 也就是还差一个才够k-2个// 是为了方便后面的操作// 从small里选一个放到big里int tmp = small.poll();smallSiz--;sum -= tmp;big.add(tmp);bigSiz++;}// 先放到big里 然后从big里面拿一个放到small就刚好k-2个if (i+dist < n) {big.add(nums[i+dist]);bigSiz++;}// 要从big里拿一个 访问big.peek()之前要先更新bigupdateBigPeek();int tmp = big.poll();bigSiz--;sum += tmp;small.add(tmp);smallSiz++;res = Math.min(res, nums[i] + nums[0] + sum);}return res;}// 每次访问small.peek()之前都要先更新smallpublic void updateSmallPeek() {// 如果small.peek()已经被删除了 那么就把它从small里移除 直到small.peek()是未被删除的元素while (smallSiz > 0 && smallMark.getOrDefault(small.peek(), 0) > 0) {int tmp = small.poll();smallMark.merge(tmp, -1, Integer::sum);}}public void updateBigPeek() {while (bigSiz > 0 && bigMark.getOrDefault(big.peek(), 0) > 0) {int tmp = big.poll();bigMark.merge(tmp, -1, Integer::sum);}}
}这个方法高效地使用了堆结构来保持每次窗口移动后,都能快速地选择出当前窗口中的k-2个最小数,而HashMap的标记删除机制则可以绕过优先队列不支持直接删除的限制。通过这个算法,你可以在移动窗口的过程中,不断更新当前窗口的最小值和,最终得到包含`nums[0]`在内的最小成本和。
思考1:为什么要用大顶堆只用小顶堆会怎么样?
因为小顶堆只能让您迅速访问堆中的最小值,而不是最大值。因此,如果窗口中有一个更小的数字需要加入到已满的小顶堆中(这时候我们需要替换掉小顶堆中最大的数字),您需要一种方式来找到小顶堆中的最大值,而大顶堆允许我们做到这一点。
思考2:bigMark.merge(tmp, -1, Integer::sum)这个是干什么
在Java中的
PriorityQueue并没有提供直接删除特定元素的操作,而是只提供了删除堆顶元素的操作。为了解决这个问题,bigMark的用途是实现“延迟删除”,这个技巧通常在优先队列中删除非顶部元素时使用。
- 检查 bigMark 是否包含密钥 tmp。
- 如果 bigMark 不包含 tmp,则将键值对(tmp,-1)插入 bigMark。
- 如果 bigMark 包含 tmp,则使用 Integer: : sum 将 bigMark 中 tmp 的现有值添加到 -1(因为 -1是合并值)。然后,这个和的结果替换 bigMark 中 tmp 键的当前值。
// 假设堆中有一个元素值为 5,现在我们要删除它:
int tmp = 5;
bigMark.merge(tmp, 1, Integer::sum); // 标记 tmp 为已删除// 当我们后续从堆中得到堆顶元素时:
updateBigPeek(); // 在访问堆顶前更新堆// updateBigPeek 的实现会检查堆顶元素是否被标记为已删除,如果是,就将其从堆中移除,
// 并在 bigMark 中更新其计数:
public void updateBigPeek() {while (bigSiz > 0 && bigMark.getOrDefault(big.peek(), 0) > 0) {int tmp = big.poll(); // 弹出堆顶元素bigMark.merge(tmp, -1, Integer::sum); // 更新 bigMark,减少删除计数}
}相关文章:

算法优化:LeetCode第122场双周赛解题策略与技巧
接下来会以刷常规题为主 ,周赛的难题想要独立做出来还是有一定难度的,需要消耗大量时间 比赛地址 3011. 判断一个数组是否可以变为有序 public class Solution {public int minimumCost(int[] nums) {if (nums.length < 3) {// 数组长度小于3时&a…...
IDEA导出jar
1、选择导出方式 2、选择Main Class 3、构建jar...
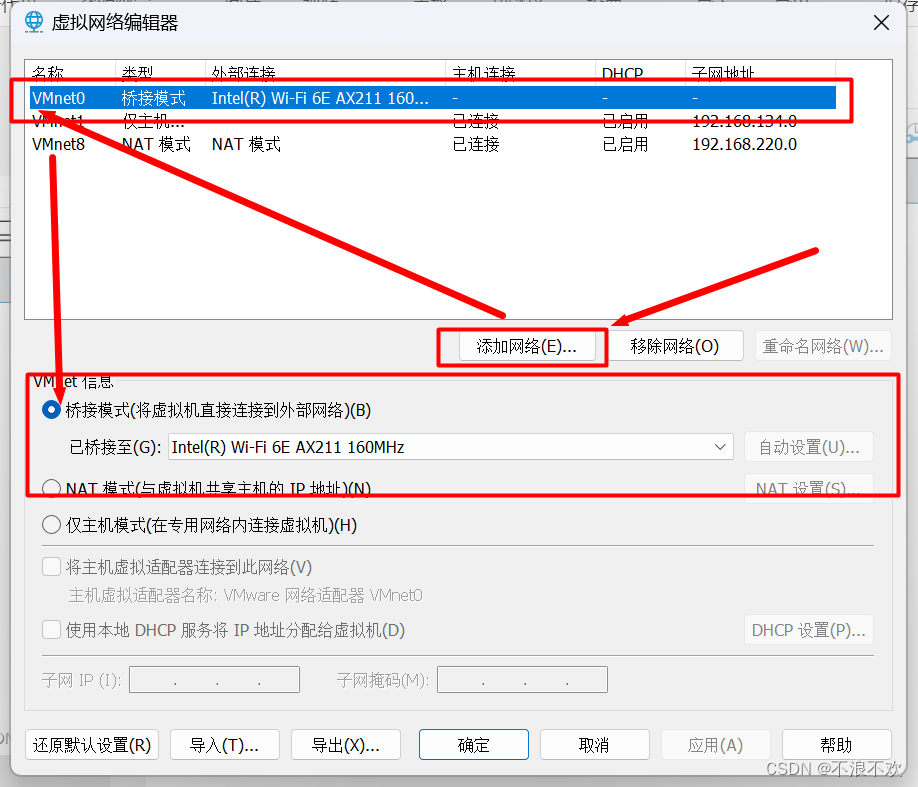
Win10/11中VMware Workstation设置网络桥接模式
文章目录 一、添加VMware Bridge Protocol服务二、配置桥接参数1.启用系统Device Install Service服务2.配置VMware 需要确认物理网卡是否有添加VMware Bridge Protocol服务 添加VMware Bridge Protocol服务 提示:以下是本篇文章正文内容,下面案例可供参…...

html Canvas粒子文字特效
代码有点长,下面是代码: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>HTML5 Canvas粒子效果文字动画特效DEMO演示</title><link rel"stylesheet" href"css/normalize.c…...

@JsonFormat失效,被jackson自定义配置覆盖
jackson配置类 我的jackson配置类如下,其中serializerByType(LocalDateTime.class, new LocalDateTimeSerializer()) 覆盖了JsonFormat注解 Configuration public class JacksonConfiguration {public static final DateTimeFormatter optionalDateTimePattern (n…...
SaaS系统如何助力企业数字化转型
随着科技的快速发展,数字化转型已经成为企业适应市场变化、提高竞争力的必要手段。在这个过程中,SaaS(软件即服务)系统以其独特的优势,正在成为越来越多企业的首选。乔拓云SaaS系统作为这一领域的佼佼者,更…...
nginx配置内网代理,前端+后端分开配置
安装好后nginx,进入配置文件 我这块安装在了home里面,各位根据自身情况选择 打开nginx.conf文件 在底部查看是否包含这段信息:含义是配置文件包含该路径下的配置文件 include /home/nginx/conf/conf.d/*.conf; # 该路径根据自己的安装位置自行修改 配置文件 进入conf.d文…...
i18n多国语言Internationalization的动态实现
一、数据动态的更新 在上一篇i18n多国语言Internationalization的实现-CSDN博客,可能会遇到一个问题,我们在进行英文或中文切换时,并没有办法对当前的数据进行动态的更新。指的是什么意思呢?当前app.js当中一个组件内容ÿ…...
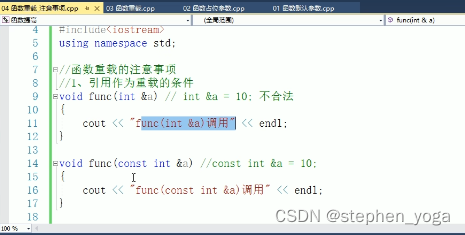
C++笔记(二)
函数的默认参数 如果我们自己传入数据,就用自己的数据,如果没有,就用默认值 语法: 返回值类型 函数名(形参默认值){} int func(int a,int b20,int c30){} …...

【技能---构建github中SSH密钥的流程】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言SSH基于账号口令的安全验证通过SSH连接到服务器打开终端(命令行界面)使用 SSH 命令连接: 在 Ubuntu 中生成 SSH 密钥并将其添…...

linux-centos服务器离线安装yapi(包含nodejs、mongodb、yapi、pm2离线安装)
yapi是使用vue框架开发的,借助nodejs 前端直接访问的mongodb数据库,离线安装yapi步骤如下 下载离线安装包 下载地址 https://download.csdn.net/download/qq445829096/88778418 离线安装包先复制到 dev/yapi目录(根据自己习惯自定义目录) node-v12.13.0-linux-x64.tar.xz …...

手撕重采样,考虑C的实现方式
一、参考文章: 重采样、上采样、下采样 - 知乎 (zhihu.com) 先直接给结论,正常重采样过程如下: 1、对于原采样率fs,需要重采样到fs1,一般fs和fs1都是整数哈,则先找fs和fs1的最小公倍数,设为m…...

网络安全产品之认识入侵防御系统
由于网络安全威胁的不断演变和增长。随着网络技术的不断发展和普及,网络攻击的种类和数量也在不断增加,给企业和个人带来了巨大的安全风险。传统的防火墙、入侵检测防护体系等安全产品在面对这些威胁时,存在一定的局限性和不足,无…...

第20课 在Android Native开发中加入新的C++类
这节课我们开始利用ffmpeg和opencv在Android环境下来实现一个rtmp播放器,与第2课在PC端实现播放器的思路类似,只不过在处理音视频显示和播放的细节略有不同。 1.压缩备份上节课工程文件夹并修改工程文件夹为demo20,将demo20导入到Eclipse或…...
)
python学习笔记11(程序跳转语句、空语句)
(一)程序跳转语句 1、break 用法:循环语句中使用,结束本层循环,一般搭配if来使用。注意while/else语法 示例: i0; while i<3:user_nameinput(请输入用户名:)pwdinput("请输入密码&a…...

C. Doremy‘s City Construction(二分图问题)
思路:把集合划分成两部分,一部分中每个数都比另一部分小,这两部分连成一个完全二分图,这种情况是最优的,还需要特判所有数都相等的情况. 代码: void solve(){int n;cin >> n;vector<int>a(n 1);for(int i 1;i < n;i )cin >> a[…...

PHP“引用”漏洞
今日例题: <?php highlight_file(__FILE__); error_reporting(0); include("flag.php"); class just4fun { var $enter; var $secret; } if (isset($_GET[pass])) { $pass $_GET[pass]; $passstr_replace(*,\*,$pass); } $o unser…...

计算机网络-AAA原理概述
对于任何网络,用户管理都是最基本的安全管理要求之一,在华为设备管理中通过AAA框架进行认证、授权、计费实现安全验证。 一、AAA概述 AAA(Authentication(认证), Authorization(授权), and Accounting(计费))是一种管理框架&#…...
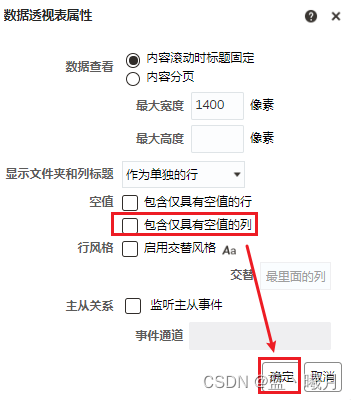
Oracle BIEE 示例(一)数据透视表2
1 背景 版本:BIEE 12C 视图:数据透视表 实现内容(顺序与具体内容不一致): 2 空列显示(方法一) 2.1 问题 列为空时,标题栏不显示信息。 2.2 期望 即使数据为空,也要显示列名。 2.3 官方资料 2.3.1 操作步骤 2.3.1.1 要在分析级别关闭空值隐藏,请执行以下操作…...
)
算法训练营Day50(动态规划11)
说明 较难,二刷再仔细打代码 123.买卖股票的最佳时机III 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 提醒 这道题一下子就难度上来了,关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次&a…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
