【学习笔记】CF1349F2 Slime and Sequences (Hard Version)
多项式工业警告!!!
点击看题意
思路来自 这位大佬 。
为什么这么好的题解没人评论。
Part 1
前置知识:拉格朗日反演(多项式复合),分式域(引入负整数次项)。
条件:有两个幂级数 F ( x ) , G ( x ) F(x),G(x) F(x),G(x),有 G ( F ( x ) ) = x G(F(x))=x G(F(x))=x,即 F , G F,G F,G互为复合逆。
F , G F,G F,G应常系数为 0 0 0且 [ x 1 ] [x^1] [x1]系数非 0 0 0。
首先引入分式域。对于无法求逆的整式 F ( x ) F(x) F(x),找出 G ( x ) = F ( x ) / x k G(x)=F(x)/x^k G(x)=F(x)/xk,则 1 F ( x ) = x − k 1 G ( x ) \frac{1}{F(x)}=x^{-k}\frac{1}{G(x)} F(x)1=x−kG(x)1。这也说明了分式域下存在负指数(这通常在对整式求逆时出现)。注意,此时乘法卷积仍然是良定义。
引理:(默认 F ( x ) F(x) F(x)满足上述条件)
[ x − 1 ] F ′ ( x ) F ( x ) k = [ k = − 1 ] [x^{-1}]F'(x)F(x)^k=[k=-1] [x−1]F′(x)F(x)k=[k=−1]
证明:当 k ≠ − 1 k\ne -1 k=−1时左式可以看作 ( 1 k + 1 F ( x ) k + 1 ) ′ (\frac{1}{k+1}F(x)^{k+1})' (k+11F(x)k+1)′,而求导不可能产生 [ x − 1 ] [x^{-1}] [x−1]项( ln ( x ) \ln (x) ln(x)是例外,但是在 x = 0 x=0 x=0处无定义,所以不合法);当 k = − 1 k=-1 k=−1时可以验证答案就是 1 1 1。
扩展拉格朗日反演:
[ x n ] H ( G ( x ) ) = 1 n [ x n − 1 ] H ′ ( x ) ( x F ( x ) ) n [x^n]H(G(x))=\frac{1}{n}[x^{n-1}]H'(x)\left(\frac{x}{F(x)}\right)^n [xn]H(G(x))=n1[xn−1]H′(x)(F(x)x)n
另类扩展拉格朗日反演:
[ x n ] H ( G ( x ) ) = [ x n ] H ( x ) ( x F ( x ) ) n + 1 F ′ ( x ) [x^n]H(G(x))=[x^n]H(x)\left(\frac{x}{F(x)}\right)^{n+1}F'(x) [xn]H(G(x))=[xn]H(x)(F(x)x)n+1F′(x)
懒得抄了,自己看command_block的博客吧
通常来讲, H ( x ) H(x) H(x)是自己构造的。求复合逆没有比较好的方法,一般要根据题目特殊性质来。一般来讲根据 H ( x ) H(x) H(x)和 F ( x ) F(x) F(x)谁的导函数比较简单来选取公式,并且显然我们也可以看出当 n = 0 n=0 n=0时只能选后面那一种公式。
比较经典的应用是有标号有根树计数。
Part 2
咕了。自己看大佬写的题解吧。感觉肯定比我写得好。
代码:
//我还真写了,居然能过。
相关文章:
)
【学习笔记】CF1349F2 Slime and Sequences (Hard Version)
多项式工业警告!!! 点击看题意 思路来自 这位大佬 。 为什么这么好的题解没人评论。 Part 1 前置知识:拉格朗日反演(多项式复合),分式域(引入负整数次项)。 条件&a…...
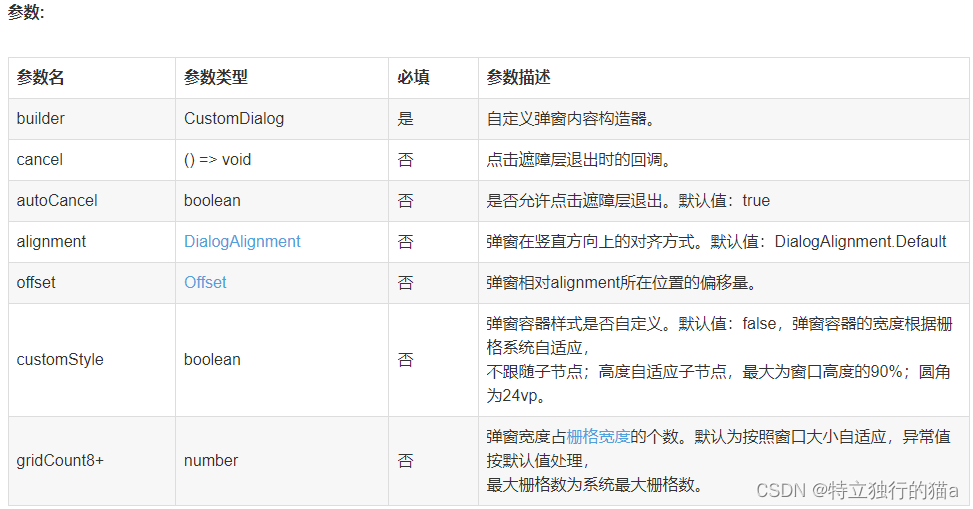
HarmonyOS 鸿蒙应用开发( 六、实现自定义弹窗CustomDialog)
自定义弹窗(CustomDialog)可用于广告、中奖、警告、软件更新等与用户交互响应操作。开发者可以通过CustomDialogController类显示自定义弹窗。具体用法请参考自定义弹窗。 在应用的使用和开发中,弹窗是一个很常见的场景,自定义弹窗…...
FileChannel)
# Java NIO(一)FileChannel
Java NIO 1.BIO与NIO的区别 BIO为阻塞IO,NIO为非阻塞IO。 BIONIOJAVA1.4之前Java 1.4之后面向流:以byte为单位处理数据面向块:以块为单位处理数据同步阻塞同步非阻塞无选择器(Selector) 1.1NIO的核心组成部分 Cha…...

[嵌入式软件][启蒙篇][仿真平台] STM32F103实现串口输出输入、ADC采集
上一篇:[嵌入式软件][启蒙篇][仿真平台] STM32F103实现LED、按键 文章目录 一、串口输出(1) 简介(2) 示例代码(3) 仿真效果 二、串口输入(1) 简介(2) 示例代码(3) 仿真效果 三、ADC采集(1) 简介(2) 采集电压(3) 示例代码(电压)(4) 仿真效果 …...

Deepin基本环境查看(四)【硬盘/分区、文件系统、硬连接/软连接】
Linux操作系统(Deepin、Ubuntu)操作系统中,硬盘分区的管理与Windows操作系统不同; 在Linux系统中维护着一个统一的文件目录体系,而硬盘和分区是以资源的形式由操作系统挂接和调度;此外Linux系统中连接(硬连…...
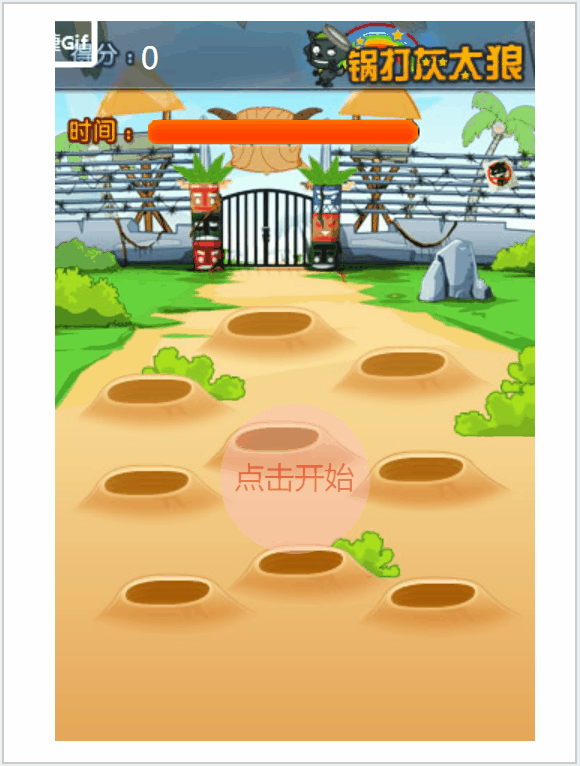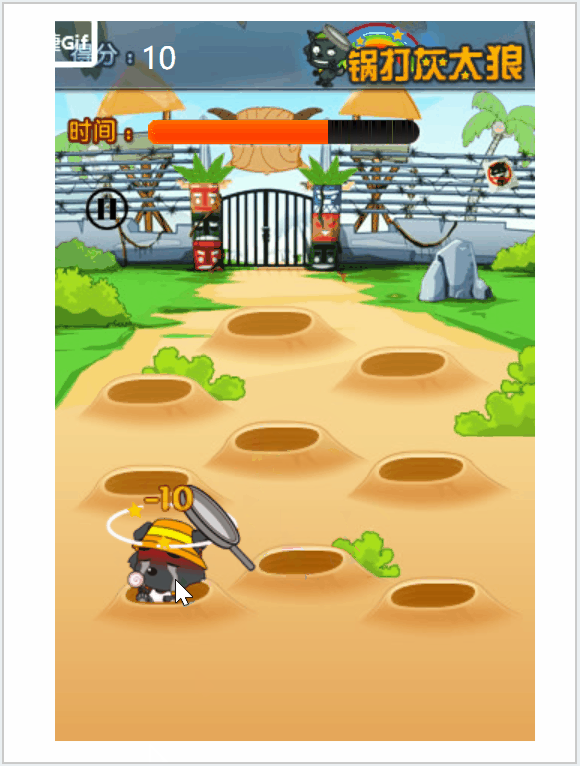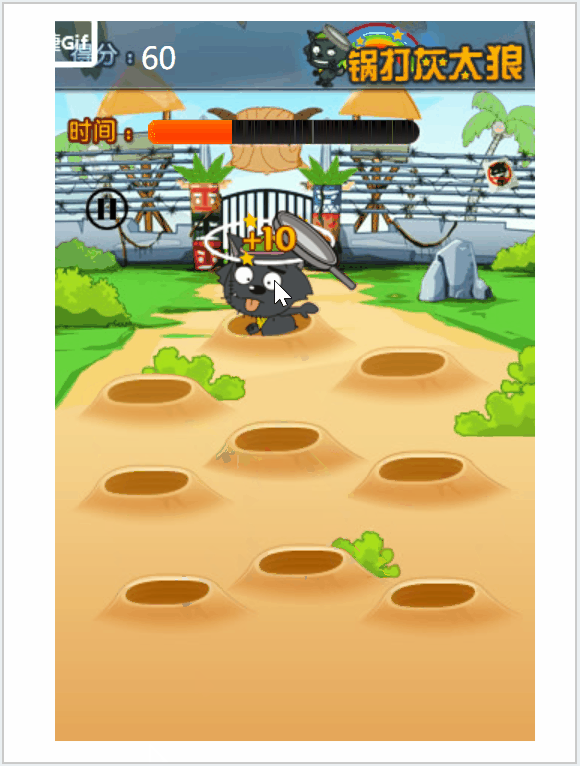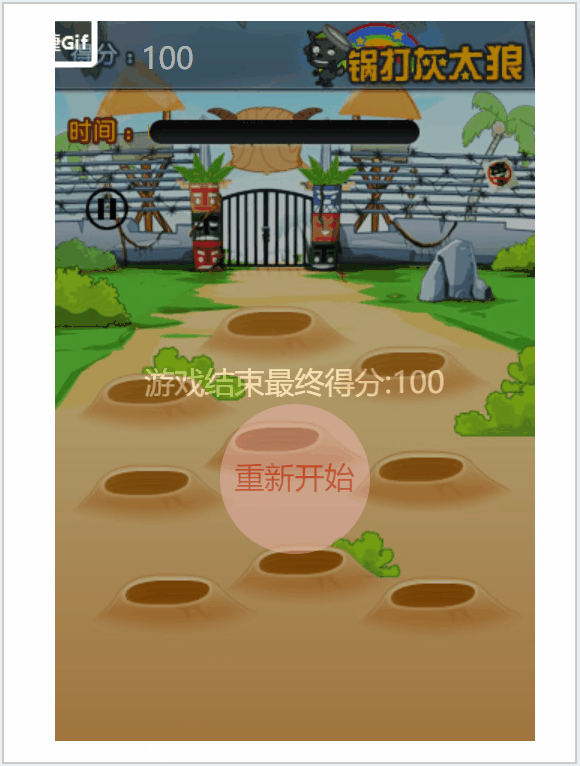
JS之打地鼠案例
需要素材的同学可以私信我 效果图: 上代码: <!DOCTYPE html> <html> <head><meta charset"utf-8"><title></title><style>* {margin: 0;padding: 0;}.box {position: relative;width: 320px;heigh…...

Kubernetes入门
k8s相关基础知识 文章目录 k8s相关基础知识1、Container2、PodPod 与 Container 的不同Pod 其它命令 3、Deployment扩容升级版本Rolling update(滚动更新)存活探针(livenessProb)就绪探针(readiness) 4、ServiceClusterIPNodePortLoadBalancer 5、Ingres…...

EtherNet/IP开发:C++搭建基础模块,EtherNet/IP源代码
这里是CIP资料的协议层级图,讲解协议构造。 ODVA(www.ODVA.org)成立于1995年,是一个全球性协会,其成员包括世界领先的自动化公司。结合其成员的支持,ODVA的使命是在工业自动化中推进开放、可互操作的信息和…...

Django(九)
1. 用户登录-Cookie和Session 什么是cookie和session? 发送HTTP请求或者HTTPS请求(无状态&短连接) http://127.0.0.1:8000/admin/list/ https://127.0.0.1:8000/admin/list/http无状态短连接:一次请求响应之后断开连接,再发请求重新连…...
)
解决Android Studio Unexpected tokens (use ; to separate expressions on the same line)
[TOC](Unexpected tokens (use ; to separate expressions on the same line)) 问题描述:Unexpected tokens (use ; to separate expressions on the same line) 原因:Android Studio 更新到最新的版本之后,gradle工程目录结构发生改变 问…...
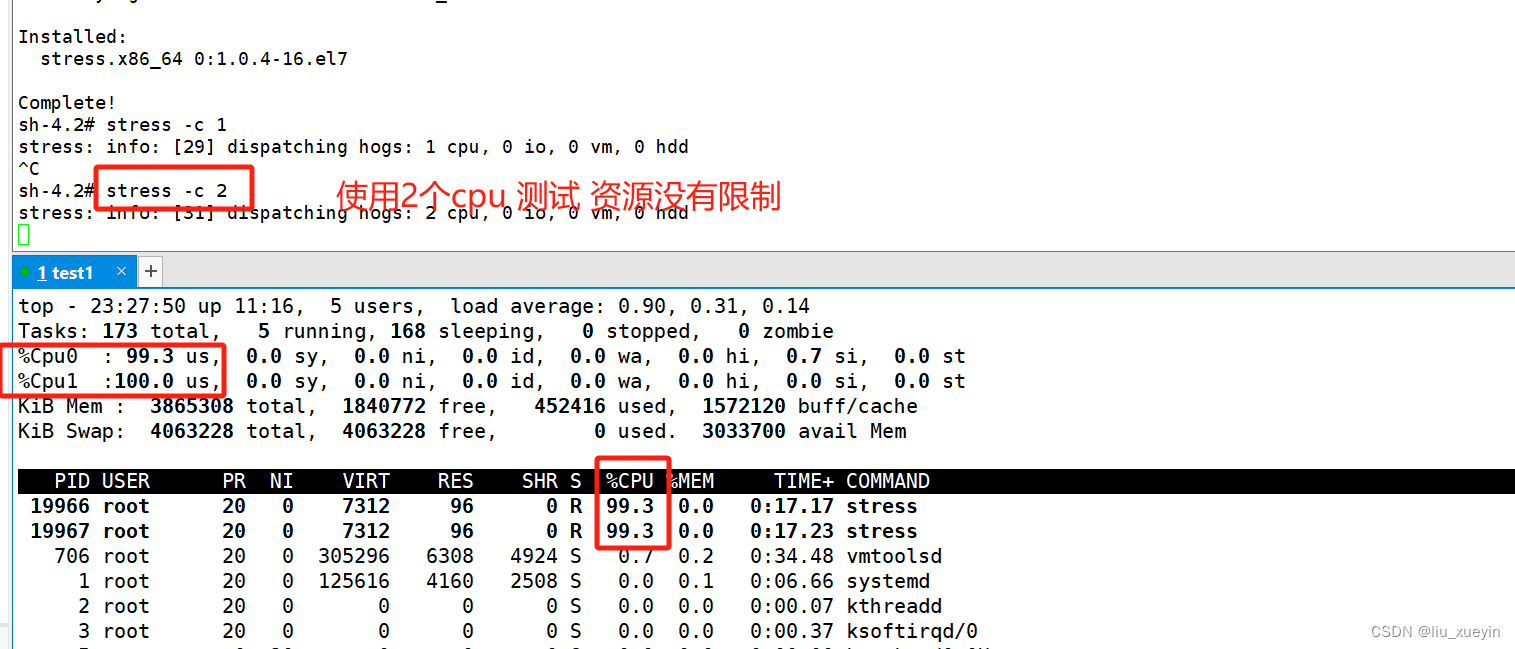
【云原生】Docker网络模式和Cgroup资源限制
目录 一、Docker 网络实现原理 二、Docker 的网络模式 #网络模式详解: 第一种:host模式 第二种:bridge模式 第三种:container模式 第四种:none模式 第五种:自定义网络 三、Cgroup资源控制 第一种&a…...

实战:加密传输数据解密
前言 下面将分享一些实际的渗透测试经验,帮助你应对在测试中遇到的数据包内容加密的情况。我们将以实战为主,技巧为辅,进入逆向的大门。 技巧 开局先讲一下技巧,掌握好了技巧,方便逆向的时候可以更加快速的找到关键…...
前端开发提高效率的两大工具
一、浏览器中的开发者工具 怎么启动开发者工具? 在浏览器中按下F12或者鼠标右键点击检查 怎么利用(常用的几点)? 1、元素 点击标红的图标可以用于在页面选择元素,同时右侧会找到元素在前端代码中的位置 点击下方红…...
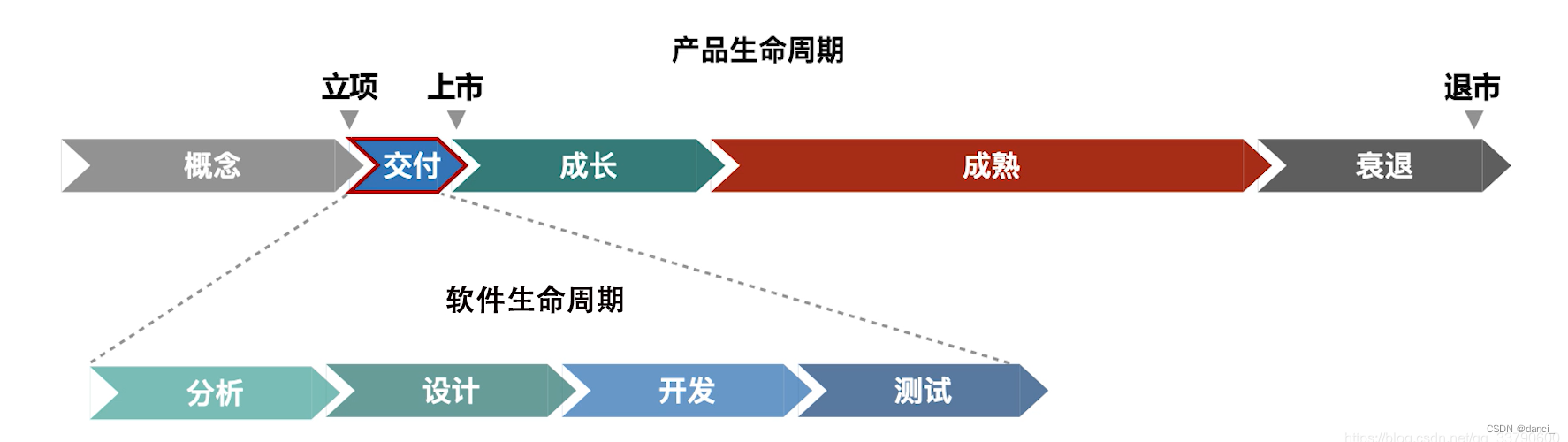
探索设计模式的魅力:深入理解面向对象设计的深层原则与思维
如何同时提高一个软件系统的可维护性 和 可复用性是面向对象对象要解决的核心问题。 通过学习和应用设计模式,可以更加深入地理解面向对象的设计理念,从而帮助设计师改善自己的系统设计。但是,设计模式并不能够提供具有普遍性的设计指导原则。…...
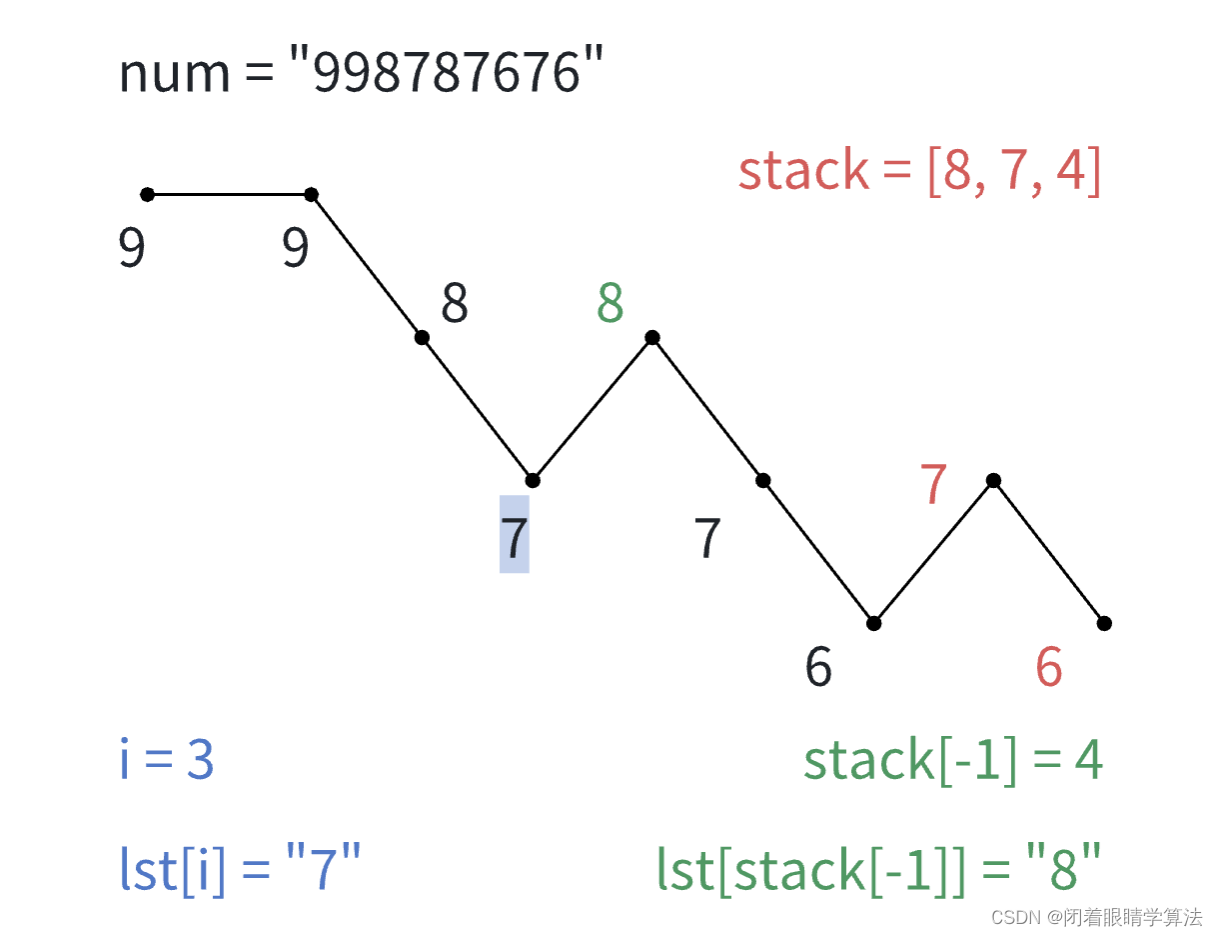
【Py/Java/C++三种语言详解】LeetCode每日一题240122【贪心】LeetCode670、最大交换
文章目录 题目链接题目描述解题思路为什么是贪心一个带图的例子 代码pythonjavacpp时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 题目链接 LeetCode670、最大交换 题目描述 给定一个非负整数数组 nums 和一个整数 k ,你需要将这个数组分成 k 个非空的连…...
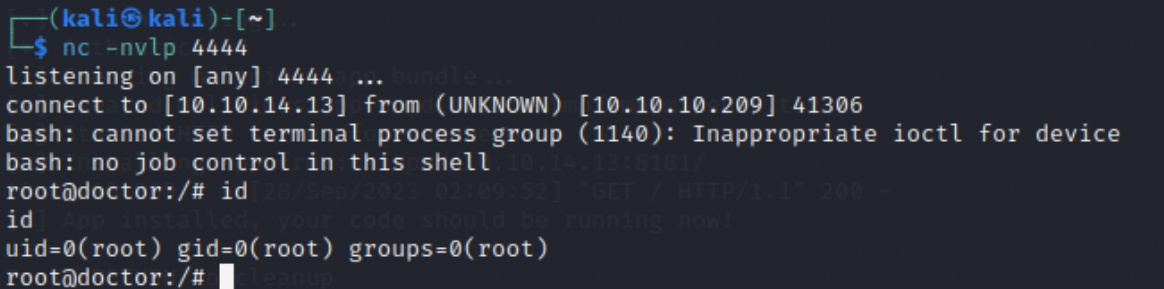
Linux/Doctor
Enumeration nmap 已知目标开放了22,80,8089端口,扫描详细情况如下 可以看到对外开放了22,80,8089三个端口 TCP/80 SSTI 访问80端口,有一个infodoctors.htb的电子邮件,点击其他的也没有什么反应,猜测有可能需要域名访问 在/et…...
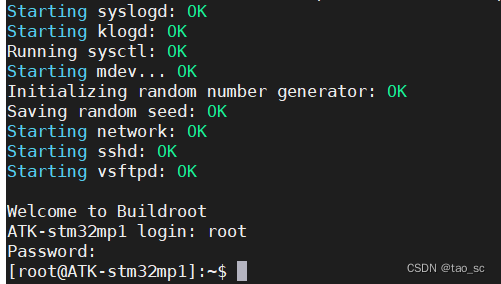
嵌入式linux学习之系统烧录
1.所需文件 1. 开发板为正点原子stm32mp157,文件可按照linux驱动教程编译,也可在正点原子文档->08、系统镜像\02、出厂系统镜像中找到: 2.烧录 1.拨码开关为000(usb启动),otg接口接入虚拟机,打开stm32cubeProgrammer: 2.页面…...
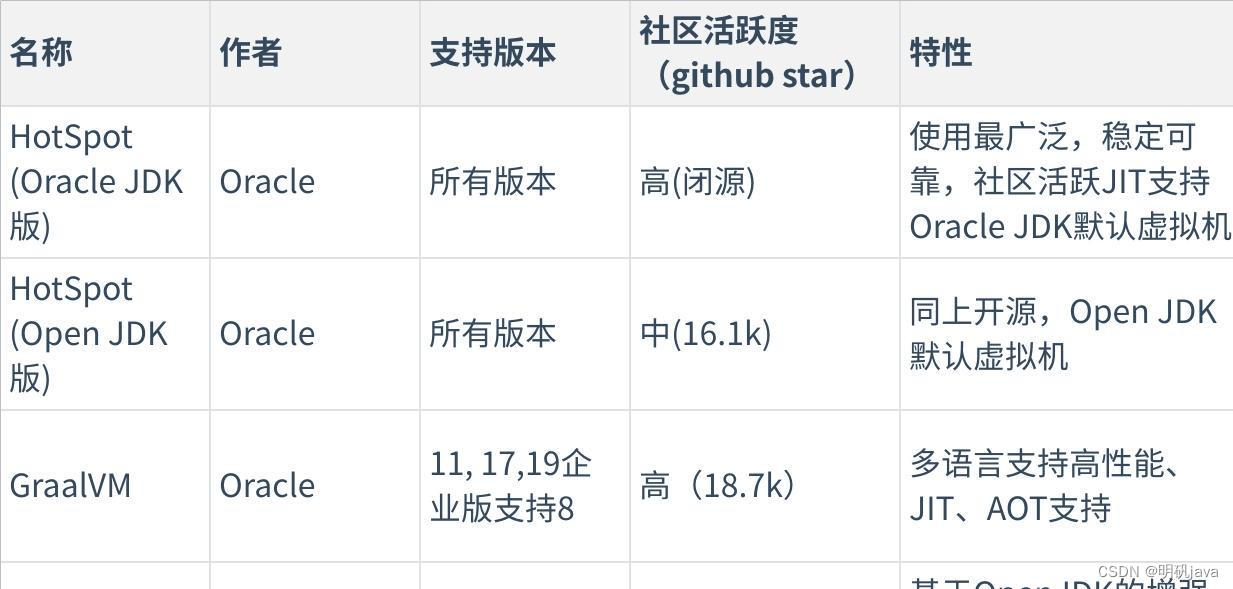
JVM-初始JVM
什么是JVM JVM 全称是 Java Virtual Machine,中文译名 Java虚拟机。JVM 本质上是一个运行在计算机上的程序,他的职责是运行Java字节码文件。 Java源代码执行流程如下: JVM的功能 1 - 解释和运行 2 - 内存管理 3 - 即时编译 解释和运行 解释…...

EXCEL VBA网抓技巧-复制网页表格,不用遍历单元格
EXCEL VBA网抓技巧-复制网页表格,不用遍历单元格 对应表格复制 Sub tableTest()Set winhttp CreateObject("winhttp.WinHttpRequest.5.1")Set HTML CreateObject("htmlfile")Set oWindow HTML.ParentWindowUrl "https://www.taiwanlo…...

动态规划——炮兵回城【集训笔记】
题目描述 游戏盘面是一个m行n列的方格矩阵,将每个方格用坐标表示,行坐标从下到上依次递增,列坐标从左至右依次递增,左下角方格的坐标为(1,1),则右上角方格的坐标为(m,n)。 游戏结束盘上只剩下一枚炮兵没有回到城池中&a…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
