无刷电机篇(一)直流无刷电机(BLDC)介绍
目录
01 直流无刷电机介绍
直流无刷电机内部结构
转子描述
定子描述
02 直流无刷电机分类
直流无刷电机分类描述
内、外转子电机描述
内、外转子电机区别
03 直流无刷电机参数
无刷电机参数
04 文章总结
大家好,这里是程序员杰克。一名平平无奇的嵌入式软件工程师。
前面电机篇已对舵机的相关内容进行了分享。从本篇开始,后续会对直流无刷电机(BLDC)进行分享。主要是按照BLDC电机介绍、原理、驱动方式、驱动算法以及最后的代码实现几个内容进行推送。本篇主要是分享直流无刷电机的结构组成、性能参数等内容。
下面正式进入本章推送的内容。
01 直流无刷电机介绍
直流无刷电机(BLDC)是同步电机中的一种,即定子产生的磁场和转子产生的磁场具有相同的频率。其因具有高输出功率、低电噪声、高可靠性、高动态响应、电磁干扰少、更好的转速-转矩等优点,而被广泛使用。
直流无刷电机内部结构
直流无刷电机的结构图如下图所示(有槽、外转子、无传感器电机为例):
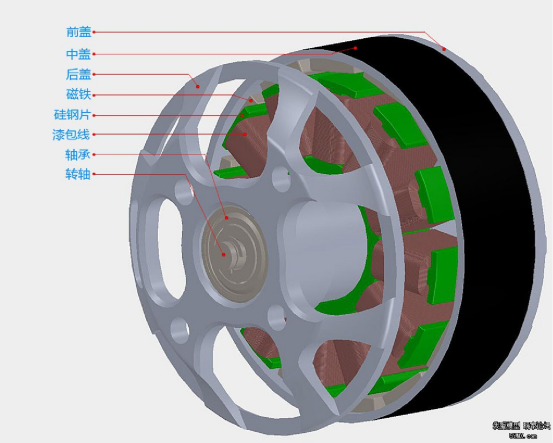
上图无刷电机由前盖、中盖、磁铁、硅钢片、漆包线、轴承、转轴以及后盖组成。其中,磁铁、轴承、转轴组成电机的转子;硅钢片、漆包线组成电机的定子;前盖、中盖、后盖组成电机的外壳。重要组成说明如下表所示:
| 组成 | 描述 | |
| 转子 | 磁铁 | 无刷电子的重要组成部分。无刷电机绝大部分性能参数都与其相关; |
| 转轴 | 转子的直接受力部分; | |
| 轴承 | 是电机运转顺畅的保证;目前大多数的无刷电机都是采用深沟球轴承; | |
| 定子 | 硅钢片 | 是有槽无刷电机的重要组成部分,主要作用是降低磁阻、参与磁路运转; |
| 漆包线 | 作为线圈绕组的通电导体;通过电流交变频率和波形,在定子周围形成磁场,驱动转子转动; |
-
转子描述
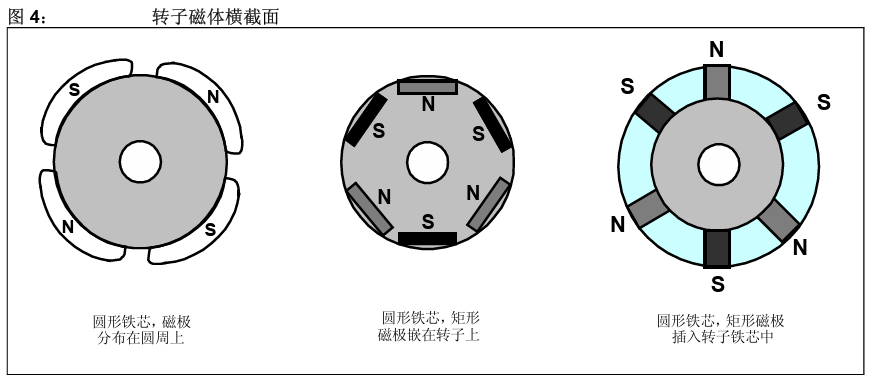
直流无刷电机(BLDC)的转子由永磁体制成,多对磁极按照N极和S极交替排列(涉及极对数参数)。
-
定子描述
直流无刷电机(BLDC)的定子由硅钢片组成(如下图),定子绕组置于沿内部轴轴向开凿的槽中(涉及铁芯极数(槽数N)参数)。每个定子绕组由许多线圈相互连接而成。常见的绕组分布呈三连接星型的方式。

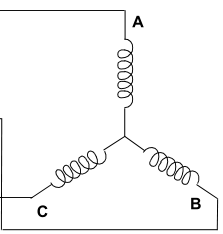
三连接星型绕组线圈,按照线圈连接的方式,可将定子绕组分为梯形、正弦波绕组。两者的区别主要是产生的反电动势的波形。顾名思义:梯形定子绕组产生梯形的反电动势,正弦波绕组产生正弦波的反电动势。如下图所示:
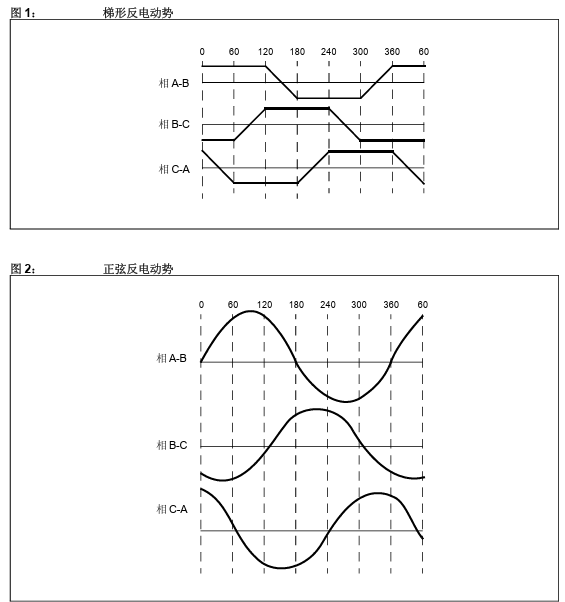
PS:电机无负载供电时,通过示波器可测出波形.
02 直流无刷电机分类
直流无刷电机分类描述
直流无刷电机(BLDC)按照转子分布可分为内转子电机、外转子电机;按照驱动相可分为单相电机、两相电机、三相电机(使用最普遍);按照是否装有传感器分为有感电机和无感电机等等;对于电机的分类有很多,篇幅原因,这里不作过来描述,感兴趣的兄弟可自行了解。
-
内、外转子电机描述
无刷电机根据转子和定子的排位结构,可分为外转子电机和内转子电机两种(如下图)。
| 电机 | 描述 |
| 外转子电机 | 内部通电线圈绕组作为定子,永磁体与外壳联动为转子;通俗来说:转子在外、定子在内; |
| 内转子电机 | 内部永磁体与转轴联动为转子,通电线圈绕组与外壳作为定子。通俗来说:转子在内、定子在外; |

-
内、外转子电机区别
内、外转子电机除了转子和定子排序不一样外,还有如下的区别:
| 特性 | 内转子电机 | 外转子电机 |
| 功率密度 | 更高 | 较低 |
| 转速 | 更高 | 较低 |
| 稳定性 | 较低 | 更高 |
| 成本 | 相对更高 | 相对更低 |
| 散热性 | 较差 | 更好 |
| 极对数 | 更少 | 更多 |
03 直流无刷电机参数
无刷电机参数
| 参数 | 描述 |
| 额定电压 | 对于无刷电机而言,其适合的工作电压非常广,此参数是指定负载条件下的工作电压. |
| KV值 | 物理意义:1V 工作电压下每分钟的转速,即: 转速(空载)= KV值 * 工作电压; 对于尺寸规格的无刷电机而言: 1. 绕线匝数多,KV值低,最高输出电流小,扭力大; 2. 绕线匝数少,KV值高,最高输出电流大,扭力小; |
| 转矩和转速 | 转矩(力矩、扭矩): 电机中转子产生的可以用来带动机械负载的驱动力矩; 转速: 电机每分钟的转速 ; |
| 最大电流 | 能够承受并安全工作的最大电流 |
| 槽极结构 | 铁芯极数(槽数N): 定子硅钢片的槽数量; 磁钢极数(极数P): 转子上磁钢的数量; |
| 定子电感 | 电动机静止时的定子绕组两端的电感 |
| 定子电阻 | 在 20℃ 下电动机每相绕组的直流电阻 |
| 反电动势系数 | 在规定条件下,电动机绕组开路时,单位转速在电枢绕组中所产生的线感应电动势值 |
04 文章总结
本篇内容仅仅是个人对直流无刷电机结构知识的认识和总结。下一篇推文会就直流无刷电机的原理进行分享,敬请期待。
特别说明:本篇推送图片来源于网络,如有侵权,请联系作者进行删除.
相关文章:

无刷电机篇(一)直流无刷电机(BLDC)介绍
目录 01 直流无刷电机介绍 直流无刷电机内部结构 转子描述 定子描述 02 直流无刷电机分类 直流无刷电机分类描述 内、外转子电机描述 内、外转子电机区别 03 直流无刷电机参数 无刷电机参数 04 文章总结 大家好,这里是程序员杰克。一名平平无奇的嵌入式软…...
【GitHub项目推荐--不错的Flutter项目】【转载】
01 可定制的图表库 FL Chart是一个高度可定制的 Flutter 图表库,支持折线图、条形图、饼图、散点图和雷达图 。 项目地址:https://github.com/imaNNeoFighT/fl_chart LineChart BarChart PieChart Sample1 Sample2 Sample3 …...

Unity UnityWebRequest 向php后端上传图片文件
之前测试功能写过一次,因为代码忘记保存,导致真正用到的时候怎么也想不起来当初怎么写的了,复现后还是写个文章记录一下,省的下次再忘记。 php后端 /*** 图片保存到本地*/ public function uploadLocalImage() {try {$img $thi…...
Vscode 顶部Menu(菜单)栏消失如何恢复
Vscode 顶部Menu(菜单)栏消失如何恢复? 首先按一下 Alt按键,看一下是否恢复了菜单栏如果恢复了想了解更进一步的设置,或是没能恢复菜单栏,可以看后续。 1.首先点击左下角 齿轮,打开settings; 或者 直接 ctrl 逗号 …...

Jenkins相关
1、Linux(Centos7)安装 jenkins (jdk1.8jenkins2.346),并配置jdk,maven,git,gitee 2、Linux(Centos7)安装 jenkins(jdk11jenkins2.375),并配置JDK,Maven,Git,GitLab 3、jenkins和jdk安装教程(安装支持jdk…...
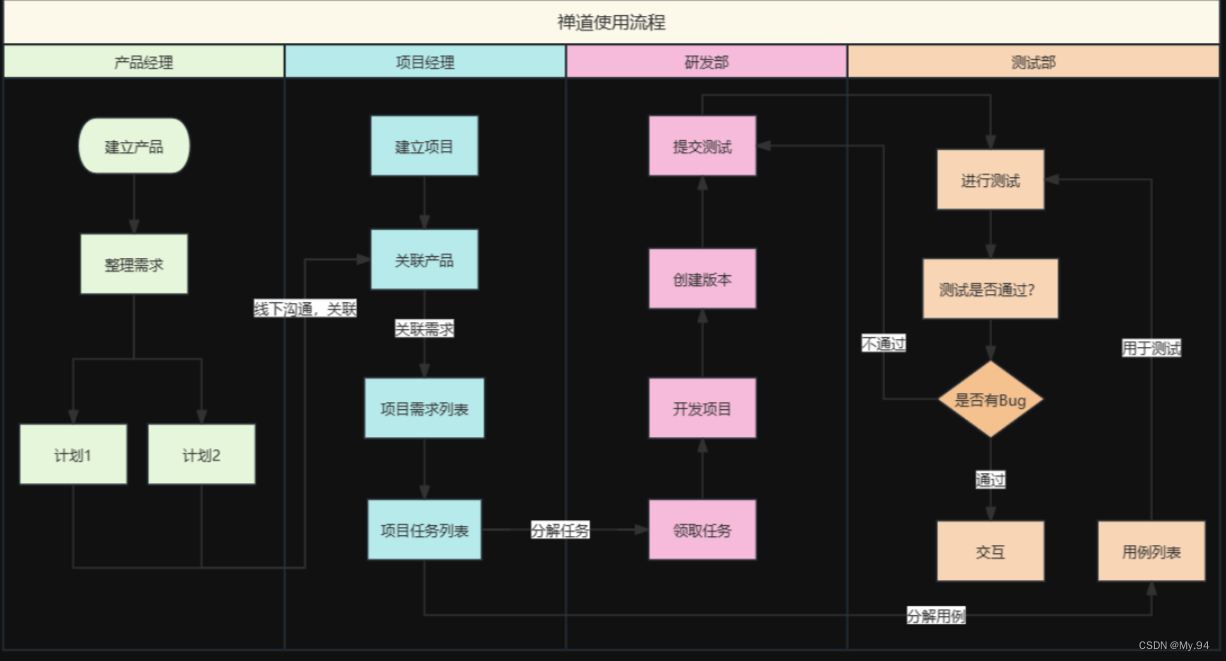
禅道的安装以及使用
一,简介 禅道是一款专业的国产开源研发项目管理软件,集产品管理、项目管理、质量管理、文档管理、组织管理和事务管理于一体,完整覆盖了研发项目管理的核心流程。管理思想基于国际流行的敏捷项目管理方法——Scrum,在遵循其价值观…...
马尔可夫预测(Python)
马尔科夫链(Markov Chains) 从一个例子入手:假设某餐厅有A,B,C三种套餐供应,每天只会是这三种中的一种,而具体是哪一种,仅取决于昨天供应的哪一种,换言之&#…...
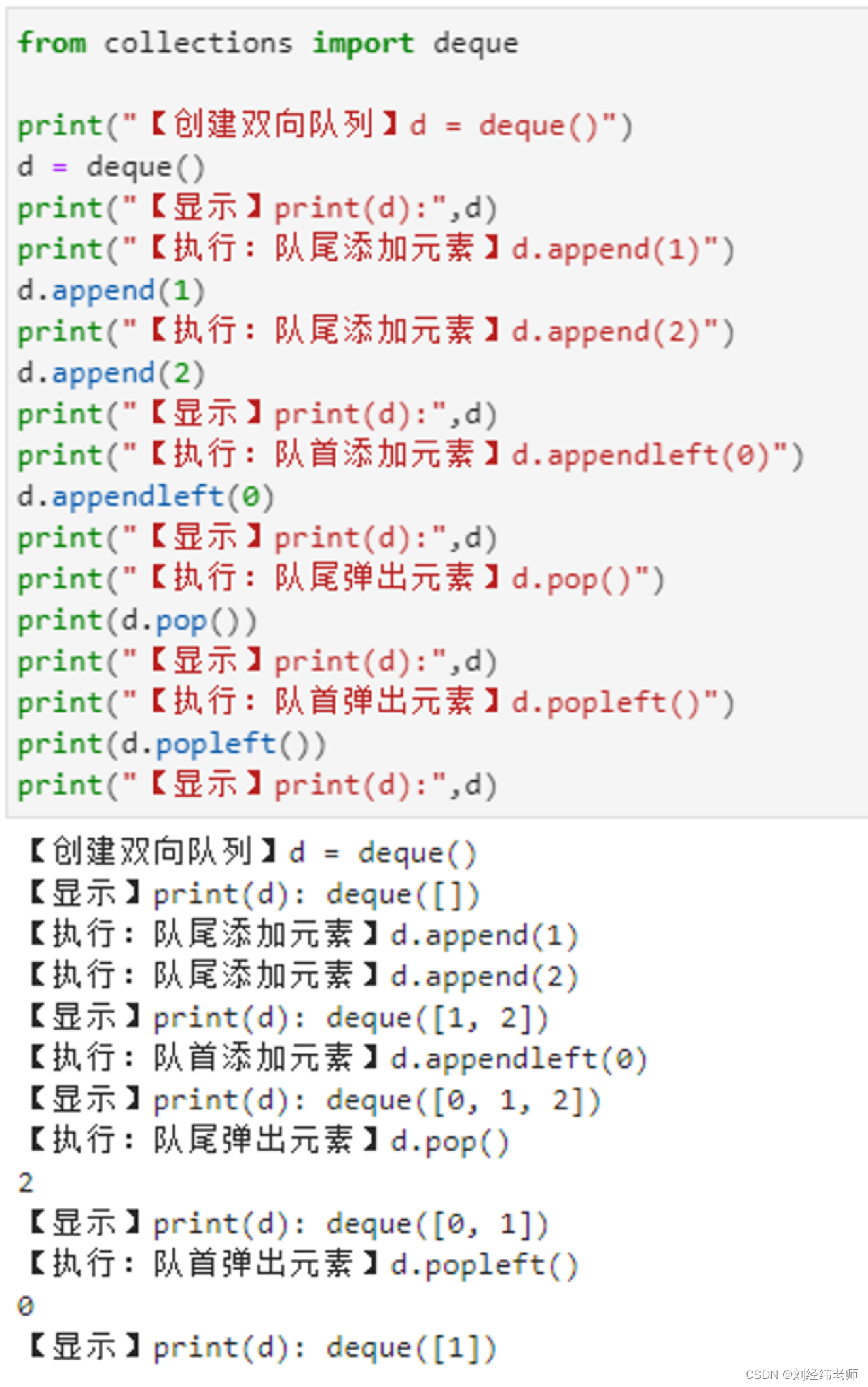
双向队列的创建队首与队尾的操作deque()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 双向队列的创建 队首与队尾的操作 deque() [太阳]选择题 请问以下代码输出的结果是? from collections import deque print("【创建双向队列】d deque()") d deque(…...
一、MongoDB、express的安装和基本使用
数据库【Sqlite3、MongoDB、Mysql】简介&小记 Sqlite3: SQLite3是一个轻量级的数据库系统,它被设计成嵌入式数据库。这意味着它是一个包含在应用程序中的数据库,而不是独立运行的系统服务。适用场景:如小型工具、游戏、本地…...

被困住了——如何从层级结构中获取子集
大家好,我是欧阳方超,我被一个问题困住了。 事情是这样的,与第三方平台对接时,第三方接口返回了一个具有层级结构的列表,比如下面这种结构: [{"id": 1,"name": "Root Category 1…...
leetcode1237. 找出给定方程的正整数解
1237. 找出给定方程的正整数解https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/ 难度中等 101 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满…...

sqlmap使用教程(6)-注入技术拓展
注入技术 选项--technique,可以用来指定SQL注入技术,默认为BEUSTQ。其中,B表示基于布尔盲注,E表示基于错误的盲注,U表示基于联合查询注入,S表示堆叠注入,T表示基于时间盲注,Q表示内联…...
苹果Find My市场需求火爆,伦茨科技ST17H6x芯片助力客户量产
苹果发布AirTag发布以来,大家都更加注重物品的防丢,苹果的 Find My 就可以查找 iPhone、Mac、AirPods、Apple Watch,如今的Find My已经不单单可以查找苹果的设备,随着第三方设备的加入,将丰富Find My Network的版图。产…...
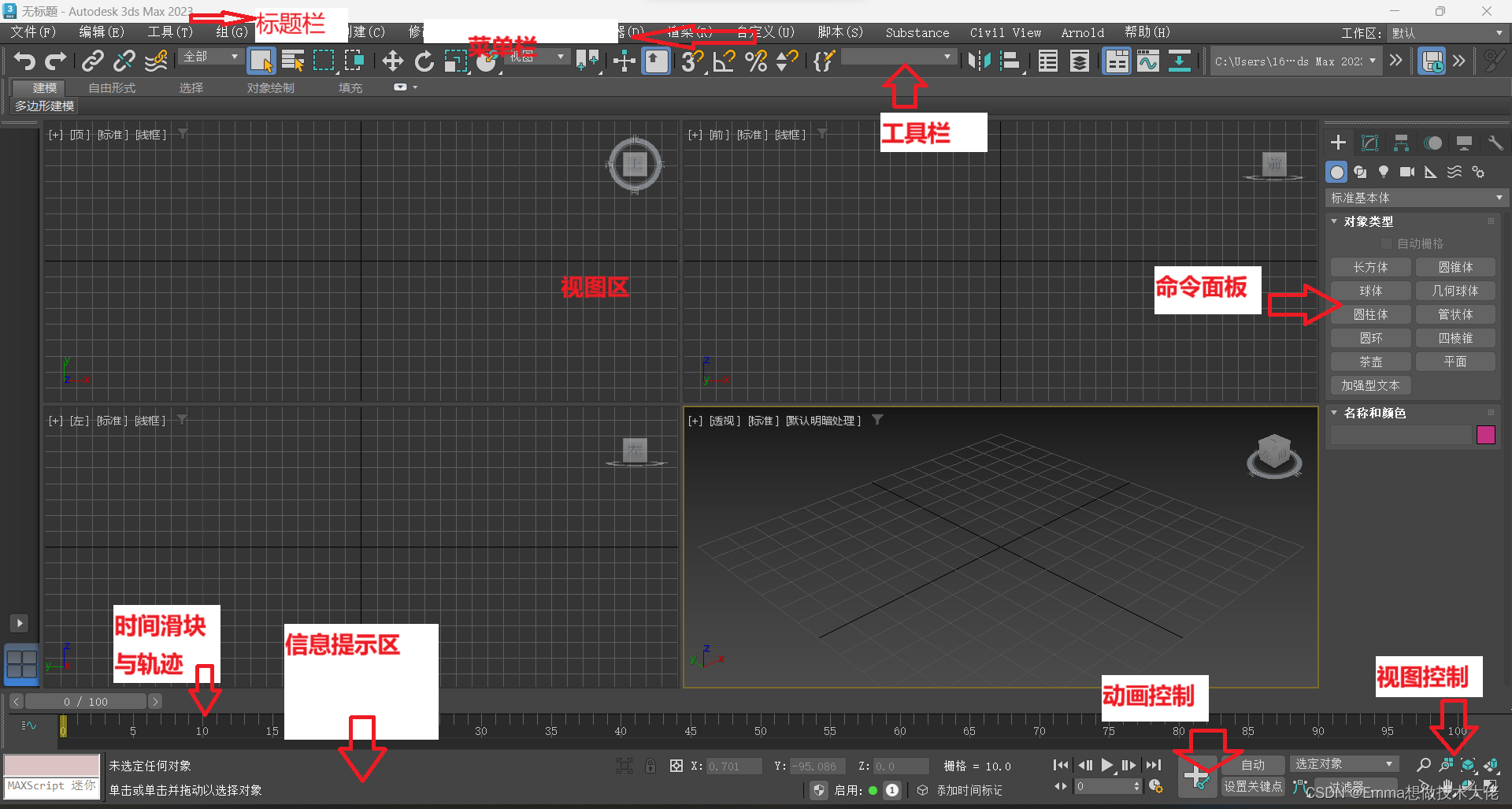
3DMAX初级小白班第一课:菜单栏介绍
基本介绍 这里不可能一个一个选项全部教给大家(毕竟之后靠实操慢慢就记住了),只说一些相对需要注意的设置。 自定义-热键编辑器-热键设置 这里有你所需要的全部快捷键 自定义-自定义UI启动布局 将UI布局还原到启动的位置 自定义-通用单…...
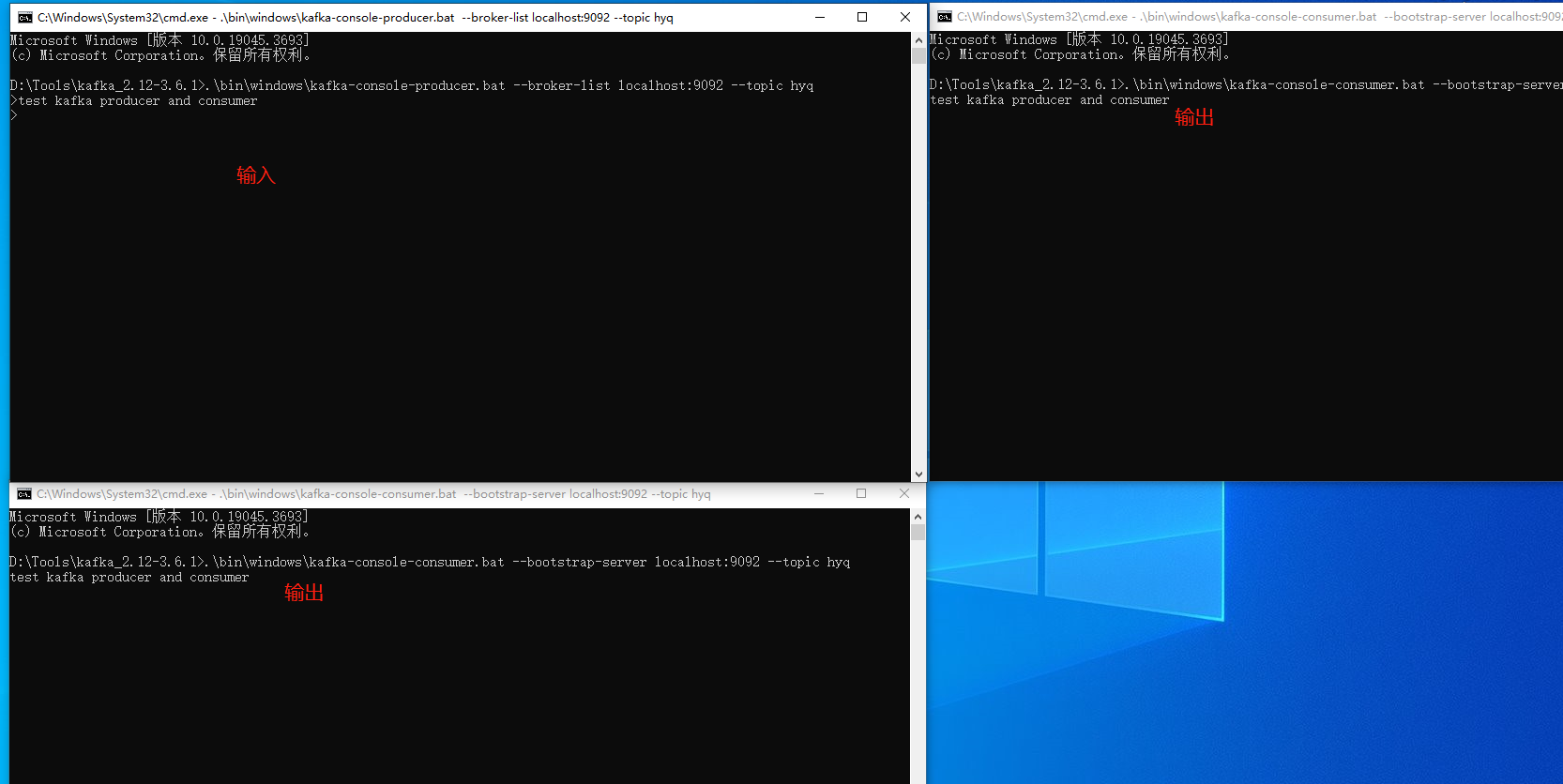
Windows中Zookeeper与kafka的安装配置
一、Zookeeper安装与使用 1.安装包下载 直接在官网下载即可Apache ZooKeeper。 下载后直接解压到本地即可。 2.环境配置 1> 在目录中下增加data和log文件夹 2> 解压目录下的 conf 目录,将目录中的 zoo_sample.cfg 文件,复制一份,重…...
QT 官方例程阅读: XML Patterns 相关
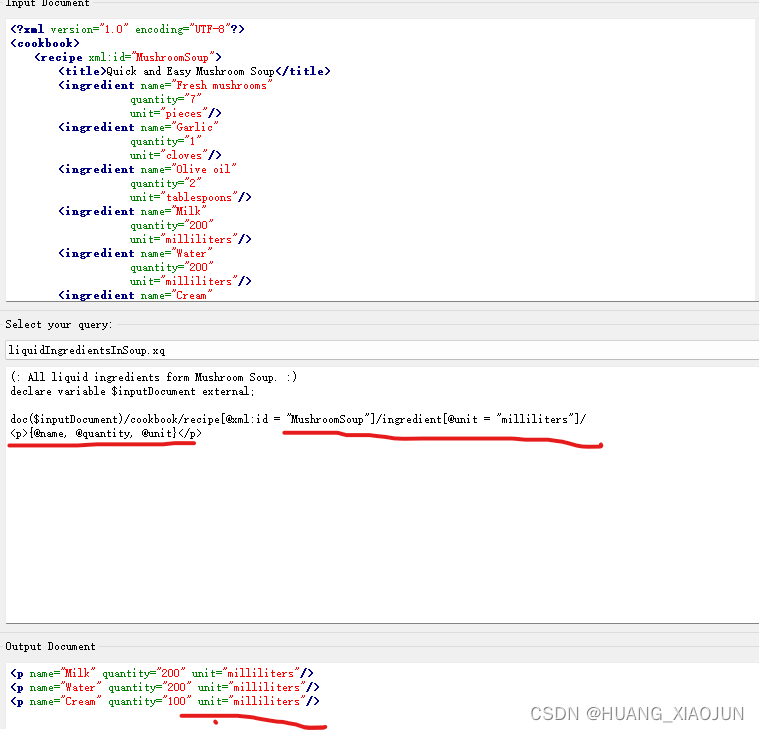
标签用于在qt creator 中查询相关工程 一、标签 Schema Validator 模式验证器 就是根据 已知的XML 模式,验证输入的XML 文件格式是否匹配,不匹配可以输出不匹配位置 如下,,首先定义了contact 元素 的子元素列表,&…...

基于SpringBoot IP黑白名单的实现
业务场景 IP黑白名单是网络安全管理中常见的策略工具,用于控制网络访问权限,根据业务场景的不同,其应用范围广泛,以下是一些典型业务场景: 服务器安全防护: 黑名单:可以用来阻止已知的恶意IP地…...
Redis客户端之Redisson(二)Redisson分布式锁
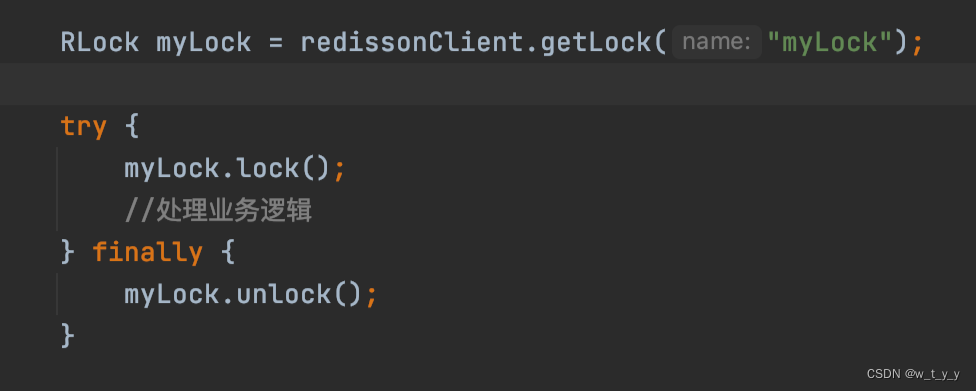
一、原理: Redisson并没有通过setNx命令来实现加锁,而是基于 Redis 看⻔狗机制,自己实现了一套分布式锁逻辑。 1、加锁机制: 二、使用方法:...
掌握大语言模型技术: 推理优化
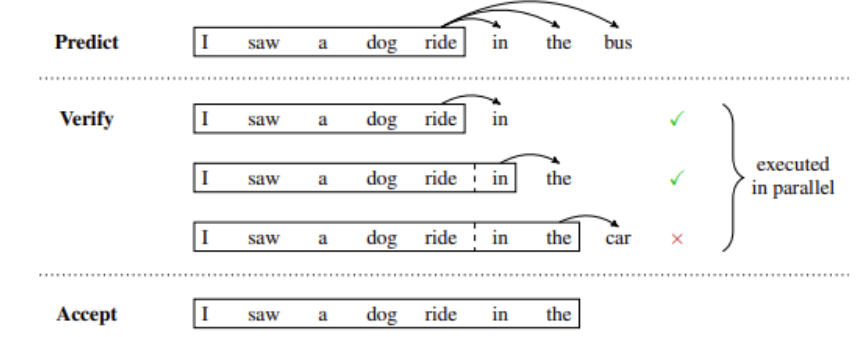
掌握大语言模型技术_推理优化 堆叠 Transformer 层来创建大型模型可以带来更好的准确性、少样本学习能力,甚至在各种语言任务上具有接近人类的涌现能力。 这些基础模型的训练成本很高,并且在推理过程中可能会占用大量内存和计算资源(经常性成…...

git如何导出提交记录及修改的文件清单?
导出git提交日志及修改文件 # 所有人的提交记录 git log --pretty=format:"%ai,%an:%s" --since="10 day ago" >> ~/Desktop/commit10.log#某一个人的提交记录 git log --pretty=format:"%ai,%an:%s" --since="30 day ago" |...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
