梯度下降法、模拟训练、拟合二次曲线、最小二乘法、MSELoss、拟合:f(x)=ax^2+bx+c
本文目标:
以这个公式为例,设计一个算法,用梯度下降法来模拟训练过程,最终得出参数a,b,c
原理介绍
目标函数:
损失函数:
,就是mse
损失函数展开:
损失函数对a,b,c求导数:
导数就是梯度,也就是目标参数与当前参数的差异,这个差异需要用梯度下降法更新
=

=

=
重复上面的过程,参数就可以更新了,然后可以看看新参数的效果,也就是损失有没有降低
具体流程
- 预设模型的表达式为:
,也就是二次函数。同时随机初始化模型参数a,b,c。如果是其他函数如
,就无法在本版本适用(修改求导方式后才可用)。即本模型需要提前知道模型的表达式。
- 通过不断喂入(x_input,y_true),得出
.而y_out与y_true之间具有差异。
- 将差异封装成一个loss函数,并分别对a,b,c进行求导。得到a,b,c的梯度
,
,
- 将
,
,
和原始的参数a,b,c和学习率作为输入,用梯度下降法来对a,b,c参数进行更新.
- 重复2,3,4过程。直到训练结束或者loss降低到较小值
python实现
# 初始化a,b,c为:-11/6 , -395/3,-2400 目标a,b,c为:(2,-4,3)
class QuadraticFunc():def drew(self,w,name="show"):a,b,c = wx1 = np.array(range(-80,80))y1 = a*x1*x1 + b*x1 + cy2 = 2*x1*x1 - 4*x1 + 3plt.clf()plt.plot(x1, y1)plt.plot(x1, y2)plt.scatter(x1, y1, c='r')# set colorplt.xlim((-50,50))plt.ylim((-500,500))plt.xlabel('X Axis')plt.ylabel('Y Axis')if name == "first":plt.pause(3)else:plt.pause(0.01)plt.ioff()#计算lossdef cal_loss(self,y_out,y_true):# return np.dot((y_out - y_true),(y_out - y_true)) * 0.5return np.mean((y_out - y_true)**2)#计算梯度 def cal_grad(self,x,y_out,y_true):# x(batch),y_out(batch),y_true(batch)a_grad = (y_out-y_true)*x**2 #b_grad = (y_out-y_true)*xc_grad = (y_out-y_true)return np.array([np.mean(a_grad),np.mean(b_grad),np.mean(c_grad)]) #梯度下降法更新参数def update_theta(self,step,w,grad):new_w = w - step*gradreturn new_wdef run(self):feed_x = np.array(range(-400,400))/400feed_y = 2*feed_x*feed_x - 4*feed_x + 3step = 0.5base_lr = 0.5lr = base_lr# 初始化参数a,b,c = -11/6 , -395/3,-2400#-1,10,26w = np.array([a,b,c])self.drew(w,"first")epochs = 100for epoch in range(epochs):# 每隔10轮 降低一半的学习率lr = base_lr/(2**(int((epoch+1)/10)))for i in range(len(feed_x)):x_input = feed_x[i]y_true = feed_y[i]y_out = w[0]*x_input*x_input +w[1]*x_input + w[2]#计算lossloss = self.cal_loss(y_out,y_true)#计算梯度grad = self.cal_grad(x_input,y_out,y_true)#更新参数,梯度下降w = self.update_theta(lr,w,grad)# self.drew(w)grad = np.round(grad,2)loss = np.round(loss,2)w = np.round(w,2)print("train times is:",epoch," grad is:",grad," loss is:","%.4f"%loss, " w is:",w,"\n")self.drew(w)if loss<1e-5:print("train finish:",w)breakdef run_batch(self):feed_x = np.array(range(-400,400))/400feed_y = 2*feed_x*feed_x - 4*feed_x + 3x_y = [[feed_x[i],feed_y[i]] for i in range(len(feed_x))]base_lr = 0.5lr = base_lr# 初始化参数a,b,c = -11/6 , -395/3,-2400#-1,10,26w = np.array([a,b,c])self.drew(w,"first")batch_size = 16data_len = len(x_y)//batch_sizeepochs = 100for epoch in range(epochs):random.shuffle(x_y)# 每隔10轮 降低一半的学习率lr = base_lr/(2**(int((epoch+1)/10)))print("epoch,lr:",epoch,lr)for i in range(data_len):x_y_list = x_y[i*batch_size:(i+1)*batch_size]x_y_np = np.array(x_y_list)x_input = x_y_np[:,0]y_true = x_y_np[:,1]y_out = w[0]*x_input*x_input +w[1]*x_input + w[2]#计算lossloss = self.cal_loss(y_out,y_true)#计算梯度grad = self.cal_grad(x_input,y_out,y_true)#更新参数,梯度下降w = self.update_theta(lr,w,grad)grad = np.round(grad,2)loss = np.round(loss,2)w = np.round(w,2)print("train times is:",epoch," grad is:",grad," loss is:","%.4f"%loss, " w is:",w,"\n")self.drew(w)if loss<1e-5:print("train finish:",w)# breaktime.sleep(0.1)if __name__ == "__main__":qf = QuadraticFunc()qf.run()
相关文章:
梯度下降法、模拟训练、拟合二次曲线、最小二乘法、MSELoss、拟合:f(x)=ax^2+bx+c
本文目标: 以这个公式为例,设计一个算法,用梯度下降法来模拟训练过程,最终得出参数a,b,c 原理介绍 目标函数: 损失函数:,就是mse 损失函数展开: 损失函数对a,b,c求导数: 导数就是梯度…...

Web3.0投票如何做到公平公正且不泄露个人隐私
在当前的数字时代,社交平台举办投票活动已成为了一种普遍现象。然而,随之而来的是一些隐私和安全方面的顾虑,特别是关于个人信息泄露和电话骚扰的问题。期望建立一个既公平公正又能保护个人隐私的投票系统。Web3.0的出现为实现这一目标提供了…...

灰度图像的自动阈值分割
第一种:Otsu (大津法) 一、基于cv2的API调用 1、代码实现 直接给出相关代码: import cv2 import matplotlib.pylab as pltpath r"D:\Desktop\00aa\1.png" img cv2.imread(path, 0)def main2():ret, thresh1 cv2.…...
利用Maven获取jar包
我有一个习惯,就是程序不在线依赖网络的任何包。以前用C#时候虽然用Nuget找包,但是添加引用后又马上把Nuget引用删了,再把Nuget下载的dll拷贝到工程再引用dll。 这样做的好处是: 1.别人得到程序代码可以直接编译,不用…...
将vue组件发布成npm包
文章目录 前言一、环境准备1.首先最基本的需要安装nodejs,版本推荐 v10 以上,因为需要安装vue-cli2.安装vue-cli 二、初始化项目1.构建项目2.开发组件/加入组件3. 修改配置文件 三、调试1、执行打包命令2、发布本地连接包3、测试项目 四、发布使用1、注册…...

江科大STM32 中
目录 6、TIM(Timer)定时器基本定时器通用定时器高级定时器示例程序(定时器定时中断&定时器外部时钟)TIM输出比较示例程序(PWM驱动LED呼吸灯&PWM驱动舵机&PWM驱动直流电机)TIM输入捕获示例程序&…...
vue+draggable+el-upload上传图片拖拽重排方法
vuedraggableel-upload上传图片拖拽重排方法 1.html <el-row><el-col><el-form-item label"添加视频/图片" prop"device_id"><div class"image-upload"><draggable v-model"fileList" update"dataDr…...

微信的新版canvas绘制的图案发生变形和偏移的问题
一,现象 this.context.beginPath(); this.context.moveTo(10, 10); this.context.lineTo(10, 100); this.context.lineTo(100, 100); this.context.lineTo(100, 10); this.context.lineTo(10, 10); this.context.stroke();本来绘制的是正方形,结果绘制出来是个矩形,边的宽度也…...

[ACM学习] 进制转换
进制的本质 本质是每一位的数位上的数字乘上这一位的权重 将任意进制转换为十进制 原来还很疑惑为什么从高位开始,原来从高位开始的,可以被滚动地乘很多遍。 将十进制转换为任意进制...

redis + 拦截器 :防止数据重复提交
1.项目用到,不是核心 我们干系统开发,不免要考虑一个点,数据的重复提交。 我想我们之前如果要校验数据重复提交要求,会怎么干?会在业务层,对数据库操作,查询数据是否存在,存在就禁止插入数据; 但是吧,我们每次crud操作都会连接…...

如何进行H.265视频播放器EasyPlayer.js的中性化设置?
H5无插件流媒体播放器EasyPlayer属于一款高效、精炼、稳定且免费的流媒体播放器,可支持多种流媒体协议播放,可支持H.264与H.265编码格式,性能稳定、播放流畅,能支持WebSocket-FLV、HTTP-FLV,HLS(m3u8&#…...

Ubuntu22.04安装4090显卡驱动
1、安装完Ubuntu系统,打完所有补丁后再进行后续操作 2、下载系统所需要的版本的NV显卡驱动,本次由于使用CUDA12.1,故选用的驱动版本为NVIDIA-Linux-x86_64-530.41.03.run 3、卸载NV驱动(只是保险起见,并不是一定会卸…...

YOLOv8优化策略:注意力涨点系列篇 | 一种轻量级的加强通道信息和空间信息提取能力的MLCA注意力
🚀🚀🚀本文改进:一种轻量级的加强通道信息和空间信息提取能力 MLCA注意力 🚀🚀🚀在YOLOv8中如何使用 1)作为注意力机制使用;2)与c2f结合使用; 🚀🚀🚀YOLOv8改进专栏:http://t.csdnimg.cn/hGhVK 学姐带你学习YOLOv8,从入门到创新,轻轻松松搞定科研…...
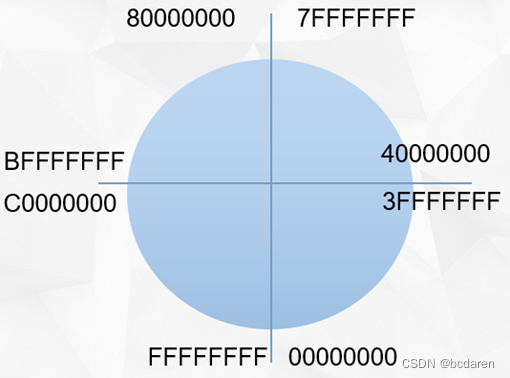
【新书推荐】2.5节 有符号整数和无符号整数
本节内容:整数的编码规则。 ■数据的编码规则:计算机的二进制数对于计算机本身而言仅仅表示0和1。人们按照不同的编码规则赋予二进制数不同的含义。整数的编码规则分为有符号整数和无符号整数。 ■数据的存储规则:x86计算机以字节为单位&…...
RT-Thread: 串口操作、增加串口、串口函数
说明:本文记录RT-Thread添加串口的步骤和串口的使用。 1.新增串口 官方链接:https://www.rt-thread.org/document/site/rtthread-studio/drivers/uart/v4.0.2/rtthread-studio-uart-v4.0.2/ 新增串口只需要在 board.h 文件中定义相关串口的宏定…...

自然语言处理的新突破:如何推动语音助手和机器翻译的进步
一、语音助手方面的进展 语音助手作为人机交互的重要入口之一,其性能的提升离不开自然语言处理技术的进步。基于深度学习的语音识别和语义理解技术,使得语音助手可以更准确地分析用户意图,提供个性化服务。 语音识别精度的持续提高 语音识别是语音助手的基础。随着深度神经网…...
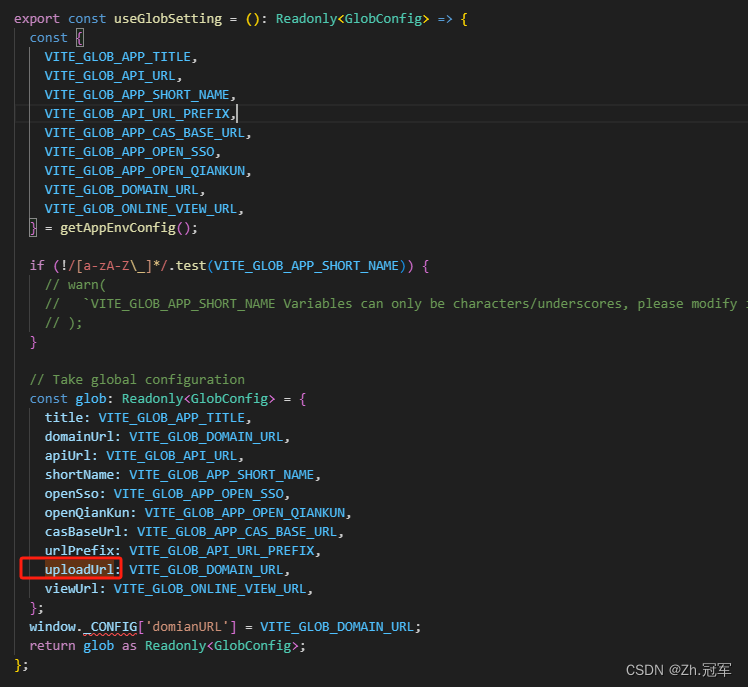
vue3 + jeecgBoot 获取项目IP地址
封装的useGlobSetting 函数 引入并使用 import { useGlobSetting } from //hooks/setting;const glob useGlobSetting();console.log(glob.uploadUrl) //http://192.168.105.57:7900/bs-axfd...
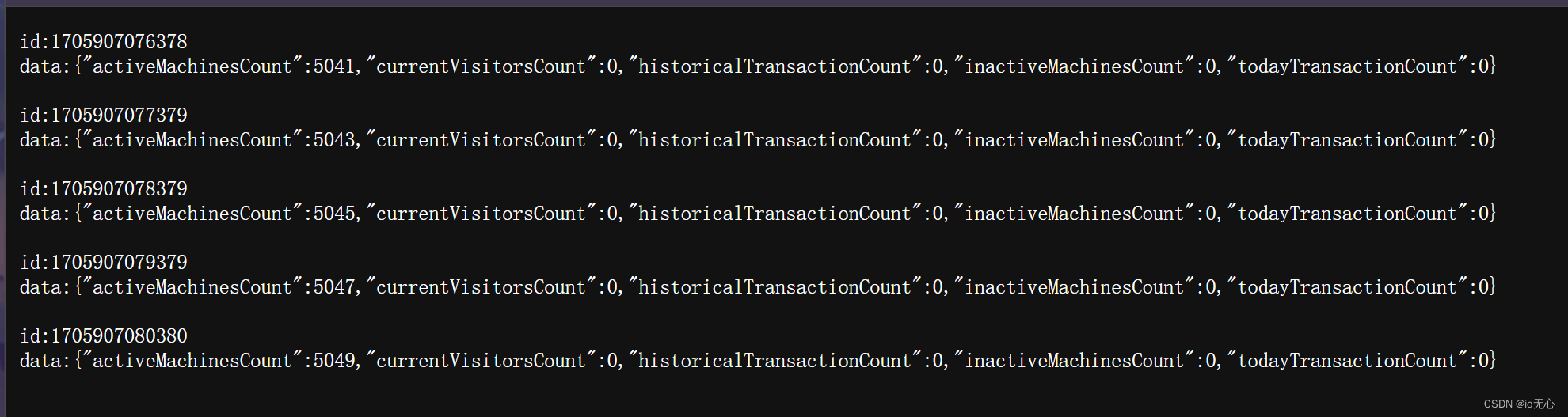
Java Server-Sent Events通信
Server-Sent Events特点与优势 后端可以向前端发送信息,类似于websocket,但是websocket是双向通信,但是sse为单向通信,服务器只能向客户端发送文本信息,效率比websocket高。 单向通信:SSE只支持服务器到客…...
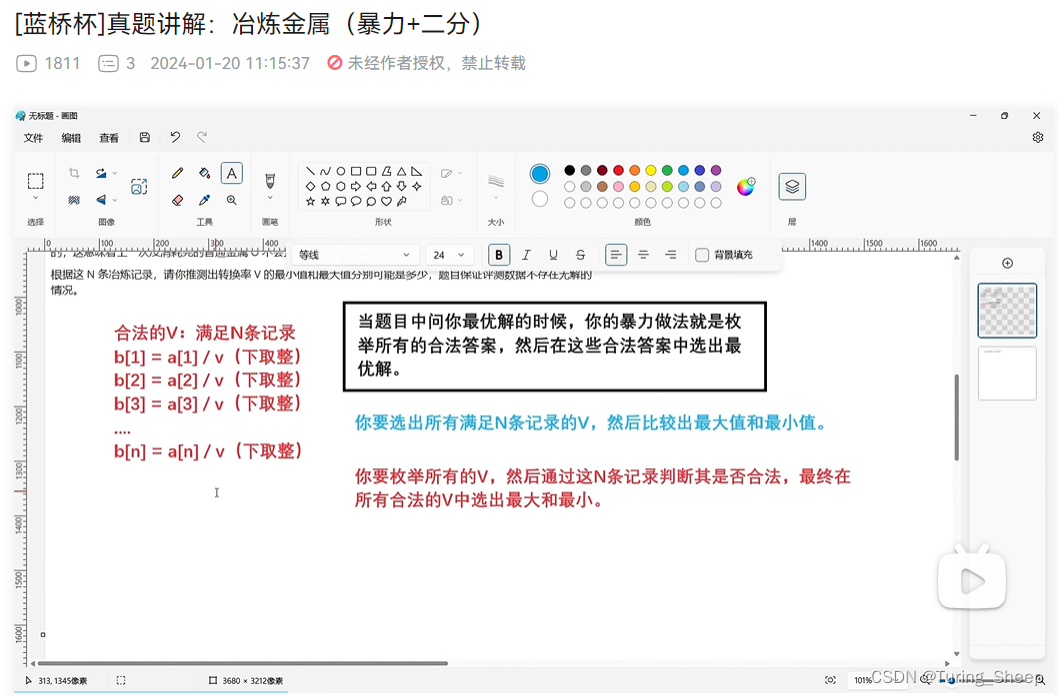
[蓝桥杯]真题讲解:冶炼金属(暴力+二分)
蓝桥杯真题视频讲解:冶炼金属(暴力做法与二分做法) 一、视频讲解二、暴力代码三、正解代码 一、视频讲解 视频讲解 二、暴力代码 //暴力代码 #include<bits/stdc.h> #define endl \n #define deb(x) cout << #x << &qu…...

Fastbee开源物联网项目RoadMap
架构优化 代码简化业务&协议解耦关键组件支持横向拓展网络协议支持横向拓展,包括:mqtt broker,tcp,coap,udp,sip等协议插件化编码脚本化业务代码模版化消息总线 功能优化 网关/子网关:上线,绑定,拓扑࿰…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
