Cantor表(刷题)(C语言)
个人博客主页:https://blog.csdn.net/2301_79293429?type=blog
专栏:https://blog.csdn.net/2301_79293429/category_12545690.html
题目描述
现代数学的著名证明之一是 Georg Cantor 证明了有理数是可枚举的。他是用下面这一张表来证明这一命题的:

我们以 Z 字形给上表的每一项编号。第一项是 1/11/1,然后是 1/21/2,2/12/1,3/13/1,2/22/2,…
输入格式
整数N(1≤N≤10^7)。
输出格式
表中的第 N 项。
输入输出样例
输入
7
输出
1/4
题目链接: 记录详情 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目分析:
将题目中的图像写为易观察的形式:
/* 1/1
1/2 2/1
3/1 2/2 1/3
设最上面一行为第1行,本题用i表示,
第i行的分子分母之和为i+1,除了第一行,偶数行的分子从1开始,奇数行从i开始
*/
AC代码:
int main()
{int n;scanf("%d", &n);if (n == 1)printf("1/1");else{int i = 0, j = 1, sum = 0;for (i = 1;; i++){sum += j++;if (sum >= n)break;}sum -= i;/*前面几行的总个数*/if (i % 2 == 1)/*奇数行*/{j = 0;if (sum == n - 1)printf("%d/%d", i, 1);else{int h = i - (n - sum) + 1;/*分子*/i = n - sum;/*分母*/printf("%d/%d", h, i);}}else{j = 0;if (sum == n - 1)printf("%d/%d", 1, i);else{int h = i - (n - sum) + 1;/*分母*/i = n - sum;/*分子*/printf("%d/%d", i, h);}}}return 0;
}
祝大家题题AC啦,天天只想做个WA梦~

相关文章:

Cantor表(刷题)(C语言)
个人博客主页:https://blog.csdn.net/2301_79293429?typeblog 专栏:https://blog.csdn.net/2301_79293429/category_12545690.html 题目描述 现代数学的著名证明之一是 Georg Cantor 证明了有理数是可枚举的。他是用下面这一张表来证明这一命题的&…...

linux install nvm
官网地址:https://github.com/nvm-sh/nvm 1、wget https://codeload.github.com/nvm-sh/nvm/tar.gz/refs/tags/v0.39.7 tar -zxvf v0.39.7 2、vim ~/.bashrc $HOMEroot export NVM_DIR"$HOME/.nvm" [ -s "$NVM_DIR/nvm.sh" ] && \…...
HTML 炫酷进度条
下面是代码 <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>Light Loader - CodePen</title><style> html, body, div, span, applet, object, iframe, h1, h2, h3, h4, h5, h6, p, blockquote, pre, a, abbr…...
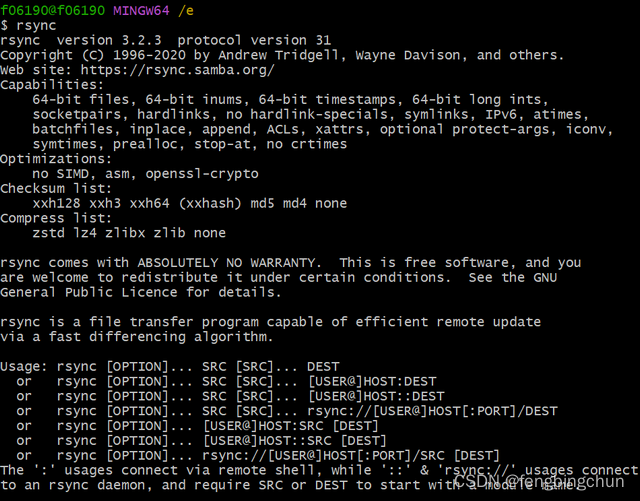
Windows10上使Git Bash支持rsync命令操作步骤
rsync命令是linux上常用的工具之一,用于远程以及本地系统中拷贝/同步文件和文件夹。 Windows Git Bash默认并不支持rsync,如下图所示: 使Git Bash支持rsync命令操作步骤: 1.从https://repo.msys2.org/msys/x86_64/ 下…...

rust for循环里的所有权 - into_iter / iter / iter_mut
文章目录 1 遍历对象实质为 .into_iter() 生成的迭代器2 避免转移 .iter() / .iter_mut()3 for循环里自变量为什么不用加mut // for循环语法糖 for loop_variable in iterator {code() } // 解糖 {let result match IntoIterator::into_iter(iterator) {mut iter > loop {m…...

GitHub README-Template.md - README.md 模板
GitHub README-Template.md - README.md 模板 1. README-Template.md 预览模式2. README-Template.md 编辑模式References A template to make good README.md. https://gist.github.com/PurpleBooth/109311bb0361f32d87a2 1. README-Template.md 预览模式 2. README-Templat…...
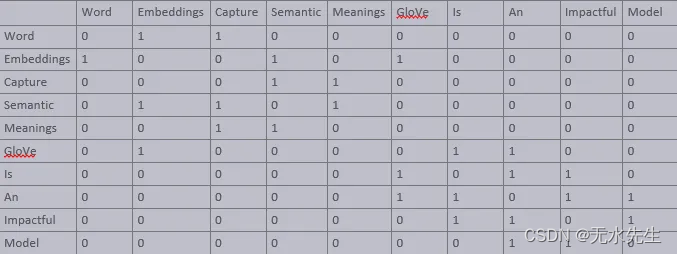
【文本到上下文 #6】Word2Vec、GloVe 和 FastText
一、说明 欢迎来到“文本到上下文”博客的第 6 个系列。到目前为止,我们已经探索了自然语言处理的基础知识、应用和挑战。我们深入研究了标记化、文本清理、停用词、词干提取、词形还原、词性标记和命名实体识别。我们的探索包括文本表示技术,如词袋、TF…...

yolov5 opencv dnn部署自己的模型
yolov5 opencv dnn部署自己的模型 github开源代码地址使用github源码结合自己导出的onnx模型推理自己的视频推理条件c部署c 推理结果 github开源代码地址 yolov5官网还提供的dnn、tensorrt推理链接本人使用的opencv c github代码,代码作者非本人,也是上面作者推荐的…...

Cortex-M4处理器 电源管理
Cortex-M4处理器的休眠模式可以降低功耗。 模式可以是以下一种或两种: 休眠模式停止处理器时钟深度睡眠模式停止系统时钟,关闭锁相环和闪存。 如果设备实现了两种提供不同级别省电的睡眠模式,那么SCR的SLEEPDEEP位将选择使用哪种睡眠模式。…...

Linux 驱动开发基础知识——编写LED驱动程序(三)
个人名片: 🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:V…...

YOLOv8 视频识别
YOLOv8 是一种目标检测算法,用于识别视频中的物体。要控制视频识别中的帧,可以通过以下方式来实现: 设置帧率:可以通过设置视频的帧率来控制视频的播放速度,从而影响视频识别的速度。 跳帧处理:可以通过跳…...
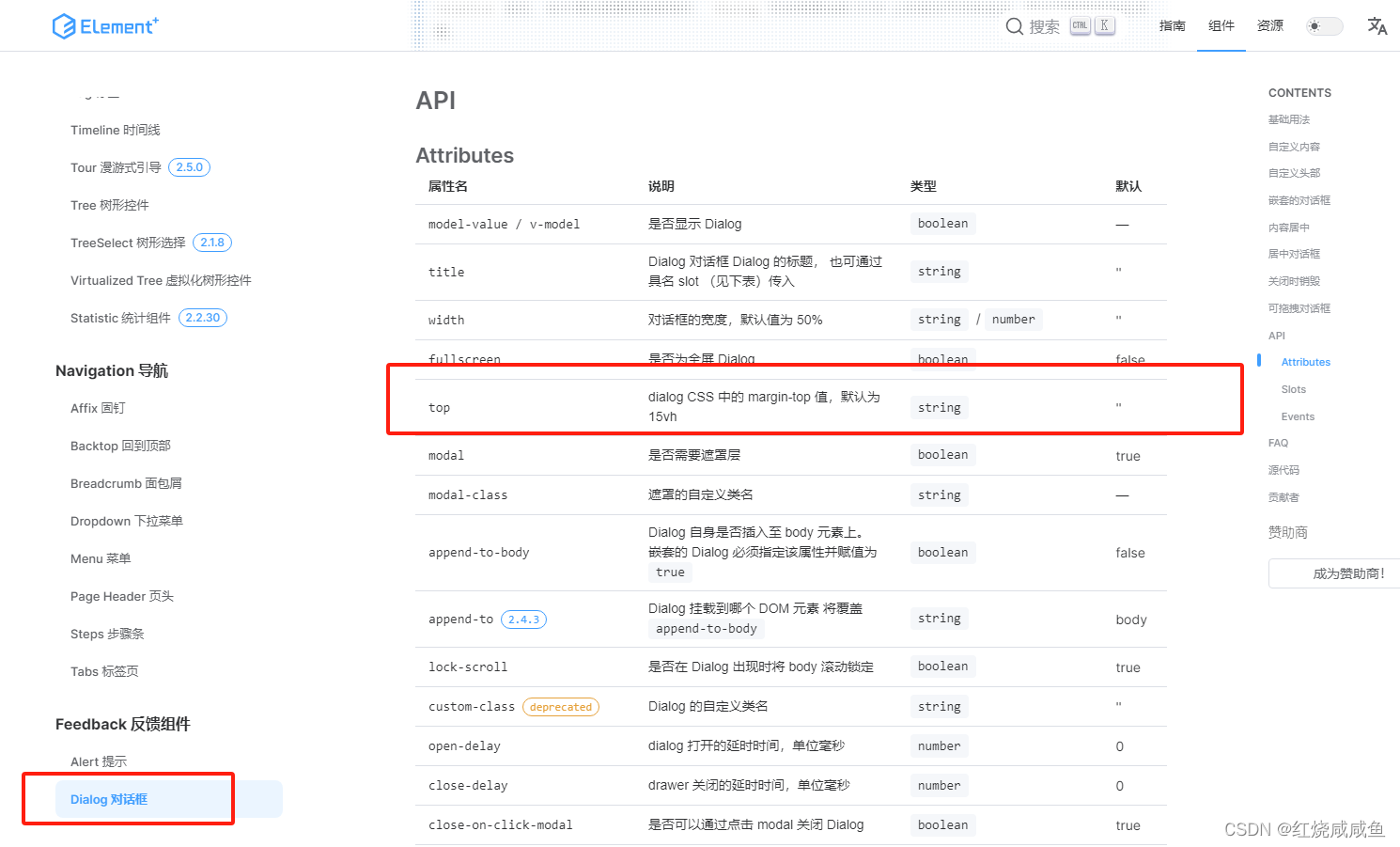
elementplus Dialog 对话框设置距离页面顶部的距离
默认为 15vh,当弹窗过于高的时候,这个距离其实是不合适的 <el-dialogv-model"dialogVisible"title"Tips"width"30%":before-close"handleClose"top"6vh"><span>This is a message</s…...
便捷接口调测:API 开发工具大比拼 | 开源专题 No.62
hoppscotch/hoppscotch Stars: 56.1k License: MIT Hoppscotch 是一个开源的 API 开发生态系统,主要功能包括发送请求和获取实时响应。该项目具有以下核心优势: 轻量级:采用简约的 UI 设计。快速:实时发送请求并获得响应。支持多…...

openssl3.2/test/certs - 008 - root-nonca trust variants: +serverAuth +anyEKU
文章目录 openssl3.2/test/certs - 008 - root-nonca trust variants: serverAuth anyEKU概述笔记END openssl3.2/test/certs - 008 - root-nonca trust variants: serverAuth anyEKU 概述 openssl3.2 - 官方demo学习 - test - certs 笔记 // \file my_openssl_win_log_doc…...
cg插画设计行业怎么样,如何学习插画设计
插画设计行业是一个充满创意和艺术性的行业,随着数字化时代的不断发展,cg插画的应用范围越来越广泛,市场需求也在逐年增长。以下是一些关于acg插画设计行业的现状和发展趋势: 市场需求不断增长:随着广告、媒体、影视、…...

1.25学习总结
今天学习了二叉树,了解了二叉树的创建和遍历的过程 今天所了解的遍历过程主要分为三种,前序中序和后序,都是DFS的想法 前序遍历:先输出在遍历左节点和右节点(输出->左->右) 中序遍历:先…...
C语言每日一题(48)回文链表
力扣 234 回文链表 题目描述 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 示例 1: 输入:head [1,2,2,1] 输出:true示例 2࿱…...

提高代码效率的5个Python内存优化技巧
大家好,当项目变得越来越大时,有效地管理计算资源是一个不可避免的需求。Python与C或c等低级语言相比,似乎不够节省内存。 但是其实有许多方法可以显著优化Python程序的内存使用,这些方法可能在实际应用中并没有人注意࿰…...
基于一款热门大屏可视化设计器使用教程
乐吾乐大屏可视化设计器是一个用于创建和定制大屏幕数据可视化展示的工具,支持零代码实现物联网、工业智能制造等领域的可视化大屏、触摸屏端UI以及工控可视化的解决方案。同时也是一个Web组态工具,支持2D、3D等多种形式,用于构建具有实时数据…...
梯度下降法、模拟训练、拟合二次曲线、最小二乘法、MSELoss、拟合:f(x)=ax^2+bx+c
本文目标: 以这个公式为例,设计一个算法,用梯度下降法来模拟训练过程,最终得出参数a,b,c 原理介绍 目标函数: 损失函数:,就是mse 损失函数展开: 损失函数对a,b,c求导数: 导数就是梯度…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
