【数学笔记】一元n次不等式,分式不等式,绝对值不等式
不等式
- 基本性质
- 一元n次不等式
- 一元二次不等式
- 一元高次不等式
- 分式不等式
- 绝对值不等式
基本性质
| 性质 |
|---|
| a > b ⇔ b < a a>b\Leftrightarrow b<a a>b⇔b<a |
| a > b , b > c ⇒ a > c a>b,b>c\Rightarrow a>c a>b,b>c⇒a>c |
| a > b , c ∈ R ⇒ a ± c > b ± c a>b,c\in R\Rightarrow a\pm c>b\pm c a>b,c∈R⇒a±c>b±c |
| a > b , c > 0 ⇒ a c > b c a>b,c>0\Rightarrow ac>bc a>b,c>0⇒ac>bc |
| a > b , c < 0 ⇒ a c < b c a>b,c<0\Rightarrow ac<bc a>b,c<0⇒ac<bc |
| a > b , c > d ⇒ a + c > b + d a>b,c>d\Rightarrow a+c>b+d a>b,c>d⇒a+c>b+d |
| a > b > 0 , c > d > 0 ⇒ a c > b d a>b>0,c>d>0\Rightarrow ac>bd a>b>0,c>d>0⇒ac>bd |
| a > b > 0 , x > 0 ⇒ a x > b x a>b>0,x>0\Rightarrow a^x>b^x a>b>0,x>0⇒ax>bx |
比较大小:
- 作差法: { a − b > 0 ⇔ a > b a − b < 0 ⇔ a < b a − b = 0 ⇔ a = b \left\{\begin{matrix} a-b>0\Leftrightarrow a>b\\ a-b<0\Leftrightarrow a<b\\ a-b=0\Leftrightarrow a=b \end{matrix}\right. ⎩ ⎨ ⎧a−b>0⇔a>ba−b<0⇔a<ba−b=0⇔a=b
- 作商法: { a b > 1 ⇔ a > b a b < 1 ⇔ a < b a b = 1 ⇔ a = b ( a ∈ R , b > 0 ) \left\{\begin{matrix} \frac{a}{b}>1\Leftrightarrow a>b\\ \frac{a}{b}<1\Leftrightarrow a<b\\ \frac{a}{b}=1\Leftrightarrow a=b \end{matrix}\right.(a\in R,b>0 ) ⎩ ⎨ ⎧ba>1⇔a>bba<1⇔a<bba=1⇔a=b(a∈R,b>0)
一元n次不等式
一元二次不等式
e.g.
a x 2 + b x + c > 0 ( a ≠ 0 ) ax^2+bx+c>0 (a\ne 0) ax2+bx+c>0(a=0)
- a > 0 a>0 a>0
设方程 a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0 存在实根,且为 x 1 , x 2 , x 1 ≤ x 2 x_1,x_2,x_1\le x_2 x1,x2,x1≤x2
显然原不等式的解集为: x ∈ ( − ∞ , x 1 ) ∪ ( x 2 , + ∞ ) x\in (-\infty,x_1)\cup(x_2,+\infty) x∈(−∞,x1)∪(x2,+∞)
若不存在实根,则解集为 x ∈ ( − ∞ , + ∞ ) x\in(-\infty,+\infty) x∈(−∞,+∞) - a < 0 a<0 a<0
设方程 a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0 存在实根,且为 x 1 , x 2 , x 1 ≤ x 2 x_1,x_2,x_1\le x_2 x1,x2,x1≤x2
显然原不等式的解集为: x ∈ ( x 1 , x 2 ) x\in(x_1,x_2) x∈(x1,x2)
若不存在实根,则解集为 x ∈ ∅ x\in\varnothing x∈∅
稍微理解一下,结合二次函数 y = a x 2 + b + c y=ax^2+b+c y=ax2+b+c的图像即可。
例题
- x 2 < 1 x^2<1 x2<1
- x 2 + 3 x + 2 ≥ 0 x^2+3x+2\ge0 x2+3x+2≥0
- x 2 + 4 x − 2 < 0 x^2+4x-2<0 x2+4x−2<0
答案:
- x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- x ∈ ( − ∞ , − 2 ] ∪ [ − 1 , + ∞ ) x\in (-\infty,-2]\cup[-1,+\infty) x∈(−∞,−2]∪[−1,+∞)
- x ∈ ( − 2 − 6 , − 2 + 6 ) x\in (-2-\sqrt6,-2+\sqrt6) x∈(−2−6,−2+6)
一元高次不等式
通常我们将其化成 ∏ i = 1 k ( x − a i ) b i \prod_{i=1}^{k}(x-a_i)^{b_i} ∏i=1k(x−ai)bi 和 0 0 0 的大小关系式,并使用穿针引线法。
比如说 ( x − 1 ) 2 ( x − 2 ) ( x − 3 ) ( x − 4 ) ≤ 0 (x-1)^2(x-2)(x-3)(x-4)\le0 (x−1)2(x−2)(x−3)(x−4)≤0
分类:
- 当 x ∈ x\in x∈ { 1 , 2 , 3 , 4 1,2,3,4 1,2,3,4}时,不等式成立。
- 当 x ∈ ( 4 , + ∞ ) x\in (4,+\infty) x∈(4,+∞)时,不等式显然不成立。
- 当 x ∈ ( 3 , 4 ) x\in(3,4) x∈(3,4)时,不等式显然成立。
- 当 x ∈ ( 2 , 3 ) x\in(2,3) x∈(2,3)时,不等式显然不成立。
- 当 x ∈ ( 1 , 2 ) x\in(1,2) x∈(1,2)时,不等式显然成立。
- 当 x ∈ ( − ∞ , 1 ) x\in(-\infty,1) x∈(−∞,1)时,不等式显然成立。
如图:

所以解集为 x ∈ ( − ∞ , 1 ] ∪ [ 1 , 2 ] ∪ [ 3 , 4 ] x\in(-\infty,1]\cup[1,2]\cup[3,4] x∈(−∞,1]∪[1,2]∪[3,4] 即 x ∈ ( − ∞ , 2 ] ∪ [ 3 , 4 ] x\in(-\infty,2]\cup[3,4] x∈(−∞,2]∪[3,4]
口诀为“奇穿偶不穿”。
分式不等式
对于一个分式方程 f ( x ) g ( x ) < 0 \frac{f(x)}{g(x)}<0 g(x)f(x)<0或 > 0 >0 >0:
因为 a b \frac{a}{b} ba 和 a b ab ab 同号,所以 f ( x ) g ( x ) > 0 ⇔ f ( x ) g ( x ) > 0 \frac{f(x)}{g(x)}>0 \Leftrightarrow f(x)g(x)>0 g(x)f(x)>0⇔f(x)g(x)>0
然后就跟上面一样了。
绝对值不等式
这个采取分类讨论,类比一下 ∣ x ∣ > 4 |x|>4 ∣x∣>4的解集即可。
相关文章:

【数学笔记】一元n次不等式,分式不等式,绝对值不等式
不等式 基本性质 一元n次不等式一元二次不等式一元高次不等式分式不等式绝对值不等式 基本性质 性质 a > b ⇔ b < a a>b\Leftrightarrow b<a a>b⇔b<a a > b , b > c ⇒ a > c a>b,b>c\Rightarrow a>c a>b,b>c⇒a>c a > b ,…...

转载-android性能优化
android性能优化 Reason: Broadcast of Intent { actandroid.intent.action.TIME_TICK ActivityManager: ANR in com.***.*** PID: 16227 Reason: Broadcast of Intent { actandroid.intent.action.TIME_TICK flg0x50000014 (has extras) }有那么一段时间我被这个ANR折磨到每…...

笔记 | Clickhouse命令行查询
在 ClickHouse 中,可以使用命令行客户端执行查询。默认情况下,ClickHouse 的命令行客户端称为 clickhouse-client。下面是一些基本的步骤和示例,用于使用 clickhouse-client 进行查询。 首先,需要确保已经安装了 ClickHouse 服务…...

Dockerfile-xxxx
1、Dockerfile-server FROM openjdk:8-jdk-alpine WORKDIR /app COPY . . CMD java -Xms1536M -Xmx1536M -XX:UseG1GC -jar -Dlog4j2.formatMsgNoLookupstrue -Dloader.pathresources,lib -Duser.timezoneGMT-05 /app/server-main-1.0.0.jar 2、Dockerfile-bgd #FROM openjdk…...

Vue中的$attrs
今天产品经理要求做保留某组件全部功能,还要在它的基础上增加东西。如果不嫌麻烦的话就笨办法,但是想一下怎么只用少量代码高效的二次封装组件呢 Vue中的$attrs 在 Vue2 中,attr 是指组件接收的 HTML 特性(attribute),通过 prop…...

使用阿里云的oss对象存储服务实现图片上传(前端vue后端java详解)
一:前期准备: 1.1:注册阿里云账号,开启对象存储oss功能,创建一个bucket(百度教程多的是,跟着创建一个就行,创建时注意存储类型是标准存储,读写权限是公共读)…...

python实例100第32例:使用a[::-1]按相反的顺序输出列表的值
题目:按相反的顺序输出列表的值。 程序分析: a[n:-n]作用是去除前n个元素和末n个元素a[-n]作用是取倒数第n个元素a[:-n]的作用是去除后n个元素a[::-1]的作用是将所有元素逆序排列a[n::-1] 的作用是从第n个元素截取后逆序排列 程序…...

python执行脚本的时候获取输入参数
当我们执行脚本的时候,通常都会执行 python test.py -i xxx -o xxx,这里的 -i 和 -o 都是输入参数,这到底是怎么传递的呢? 本文纯粹记录一下 import argparseif __name__ __main__:print("hello")# 创建AugumentParser…...

Halcon指定区域的形状匹配
Halcon指定区域的形状匹配 文章目录 Halcon指定区域的形状匹配1.在参考图像中选择目标2.创建模板3.搜索目标 在这个实例中,会介绍如何根据选定的ROI选择合适的图像金字塔参数,创建包含这个区域的形状模板,并进行精确的基于形状模板的匹配。最…...
Linux——常用命令
1、命令的基本格式 对服务器来讲,图形界面会占用更多的系统资源,而且会安装更多的服务、开放更多的端口,这对服务器的稳定性和安全性都有负面影响。其实,服务器是一个连显示器都没有的家伙,要图形界面干什么ÿ…...
外包干了2个月,技术反而退步了...
先说一下自己的情况,本科生,19年通过校招进入广州某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
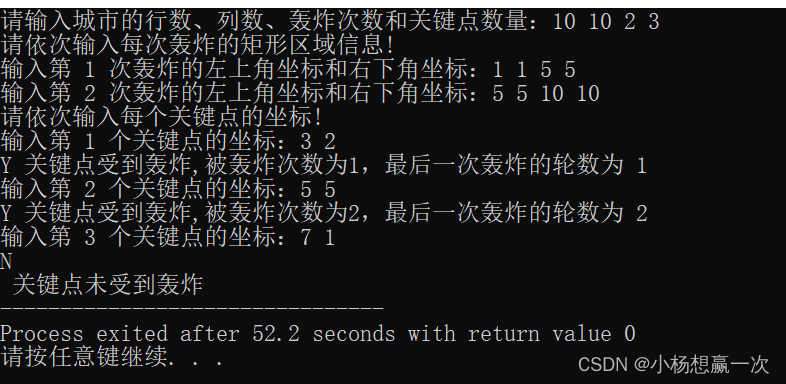
洛谷C++简单题练习day6—P1830 城市轰炸
day6--P1830 城市轰炸--1.26 习题概述 题目背景 一个大小为 nm 的城市遭到了 x 次轰炸,每次都炸了一个每条边都与边界平行的矩形。 题目描述 在轰炸后,有 y 个关键点,指挥官想知道,它们有没有受到过轰炸,如果有&a…...

【linux-interconnect】What NVIDIA MLNX_OFED is?
NVIDIA MLNX_OFED Documentation v23.07 - NVIDIA Docs 文章目录 What NVIDIA MLNX_OFED is?Overview[Software Download](https://docs.nvidia.com/networking/display/mlnxofedv23070512#src-2396583107_NVIDIAMLNX_OFEDDocumentationv23.07-SoftwareDownload) Wh…...

Unity开发中的XML注释
在Unity开发中,XML注释主要用于C#脚本的注释,以帮助生成代码文档和提供IntelliSense功能。以下是一些关于如何使用XML注释的技巧: 创建注释: 在C#中,XML注释是由///或/**...*/开始的。例如 /// <summary> /// 这…...

[MQ]常用的mq产品图形管理web界面或客户端
一、MQ介绍 1.1 定义 MQ全称为Message Queue,消息队列是应用程序和应用程序之间的通信方法。 如果非要用一个定义来概括只能是抽象出来一些概念,概括为跨服务之间传递信息的软件。 1.2 MQ产品 较为成熟的MQ产品:IBMMQ(IBM We…...
)
JWT令牌(JSON Web Token)
目录 1 前言 2 JWT令牌的组成 3 使用步骤举例 3.1 pom.xml中引入依赖 3.2 JWT生成 3.3 JWT验证 4 实践中的使用举例 4.1 拦截非法访问 4.1.1 编写为工具类 4.1.2 下发给用户 4.1.3 编写拦截器 4.1.4 注册拦截器 4.2 获取相关数据提升效率 1 前言 在我们编写的后端…...
华硕ASUS K43SD笔记本安装win7X64(ventoy为入口以支撑一盘多系统);友善之臂mini2440开发板学习
记录 老爷机 白色 华硕 K43SD 笔记本 安装 win7X64 1. MBR样式常规安装win7X64Sp1 (华硕 K43SD 安装 win7X64 ) 老爷机 白色 华硕 K43SD 笔记本 安装 win7X64 (常规安装) 设置: 禁用UEFI 启用AHCI ventoy制作MBR(非UEFI)方式的启动U盘 U盘中放cn_windows_7_ultimate_wit…...
)
npm设置源(原淘宝源域名已过期)
今天打包机器报错, Couldnt find package "antd-mobile2.3.4" required by "neo-ui-mf-base1.0.41" on the "npm" registry. 找不到antd mobile的包,查看源发现淘宝域名npm.taobao.org 和 registry.npm.taobao.org 域名…...

操作系统-进程通信(共享存储 消息传递 管道通信 读写管道的条件)
文章目录 什么是进程通信为什么进程通信需要操作系统支持共享存储消息传递直接通信方式间接通信方式 管道通信小结注意 什么是进程通信 分享吃瓜文涉及到了进程通信 进程通信需要操作系统支持 为什么进程通信需要操作系统支持 进程不能访问非本进程的空间 当进程P和Q需要…...
NODE笔记 2 使用node操作飞书多维表格
前面简单介绍了node与简单的应用,本文通过结合飞书官方文档 使用node对飞书多维表格进行简单的操作(获取token 查询多维表格recordid,删除多行数据,新增数据) 文章目录 前言 前两篇文章对node做了简单的介绍ÿ…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
