统计学-R语言-7.3
文章目录
- 前言
- 总体方差的检验
- 一个总体方差的检验
- 两个总体方差比的检验
- 非参数检验
- 总体分布的检验
- 正态性检验的图示法
- Shapiro-Wilk和K-S正态性检验
- 总体位置参数的检验
- 练习
前言
本篇文章继续对总体方差的检验进行介绍。
总体方差的检验

一个总体方差的检验
在生产和生活的许多领域,方差的大小是否适度是需要考虑的一个重要因素。一个方差大的产品意味着其质量或性能不稳定。相同均值的产品,方差小的自然要好些。与总体方差的区间估计类似,一个总体方差的检验也是使用 分布。此外,总体方差的检验,不论样本量n是大还是小,都要求总体服从正态分布。检验统计量为
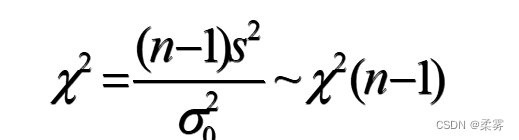
对于设定的显著性水平 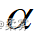 ,双侧检验的拒绝域如下图所示。对于单侧检验拒绝域在分布一侧的尾部
,双侧检验的拒绝域如下图所示。对于单侧检验拒绝域在分布一侧的尾部
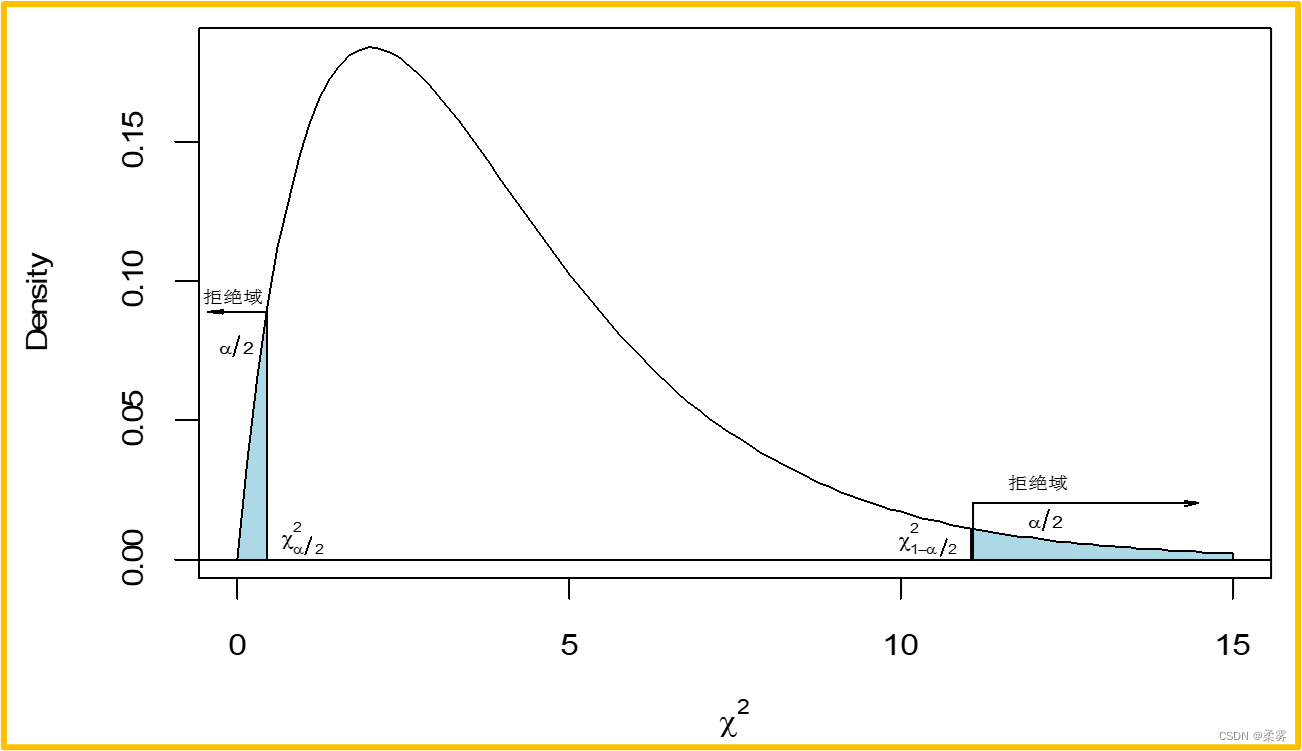
例题:
啤酒生产企业采用自动生产线灌装啤酒,每瓶的填装量为640ml,但由于受某些不可控因素的影响,每瓶的填装量会有差异。如果 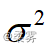 很大,会出现填装量太多或太少的情形,这样,要么生产企业不划算,要么消费者不满意。假定生产标准规定每瓶填装量的方差不应超过16。企业质检部门抽取了10瓶啤酒进行检验,得到的样本数据如下。检验填装量的方差是否符合要求( =0.05)
很大,会出现填装量太多或太少的情形,这样,要么生产企业不划算,要么消费者不满意。假定生产标准规定每瓶填装量的方差不应超过16。企业质检部门抽取了10瓶啤酒进行检验,得到的样本数据如下。检验填装量的方差是否符合要求( =0.05)
638.3 642.0 640.4 641.1 637.2 643.3 643.7 640.5 639.8 644.2
sigma.test(x,sigmasq= ,alternative=" ")

load("C:/example/ch6/example6_11.RData")
library(TeachingDemos)
sigma.test(example6_11$填装量,sigmasq=16,alternative="greater")
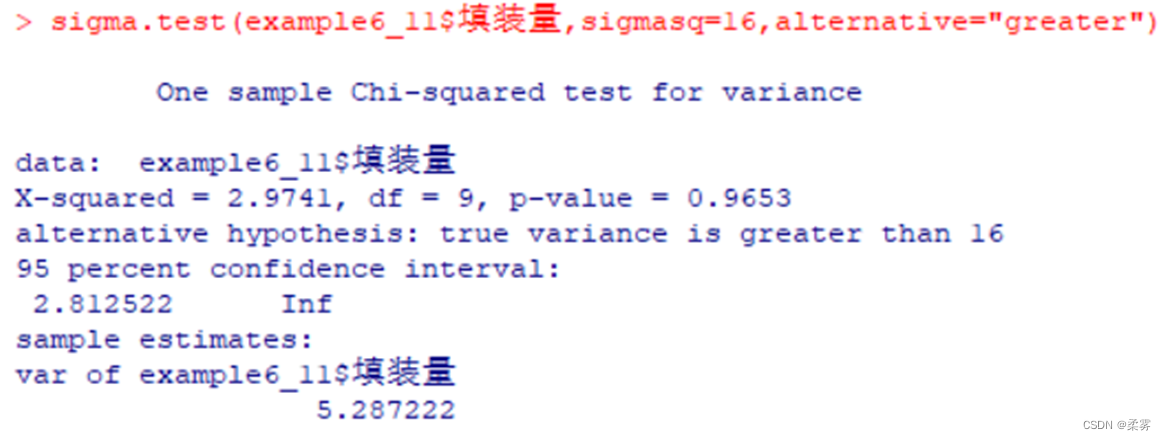

两个总体方差比的检验

(数据: example6_6. RData)沿用例6-6。检验两家企业灯泡使用寿命的方差是否有显著差异( 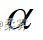 =0.05)
=0.05)

load("C:/example/ch6/example6_6.RData")
var.test(example6_6[,1],example6_6[,2],alternative="two.sided")


非参数检验
以上介绍的参数检验(如t检验、F检验等)通常是在假定总体服从正态分布或总体分布形式已知的条件下进行的、而且要求所分析的数据是数值的。
当总体的概率分布形式未知、或者无法对总体的概率分布做出假定时,参数检验方法往往会失效,这时可采用非参数检验。非参数检验方法不仅对总体的分布要求很少,对数据类型的要求也比参数检验宽松。当数据不适合用参数检验时,非参数检验往往能得出理想的结果。本篇主要介绍总体分布的检验以及几种常用的参数检验的替代方法。
总体分布的检验
在实际问题中,除了关心总体参数外,还会关心总体的分布,比如,总体是否服从正态分布,两个总体的分布是否相同,等等。
介绍检验正态性的几种方法,它是根据样本数据检验总体是否服从正态分布,或者说样本数据是否来自正态总体,检验方法有图示法和检验法。图示法主要有Q-Q图和P-P图,检验法主要有 Shapiro-Wilk检验和 Kolmogorov- Smirnov检验(K-S检验)等。
正态性检验的图示法
判断数据是否服从正态分布的描述性方法之一,就是画出数据频数分布的直方图或茎叶图,若数据近似服从正态分布,则图形的形状与正态曲线应该相似。但实际中更常用的方法是绘制样本数据的正态概率图( normal probability plots)。正态概率图有两种画法,一种称为Q-Q图( quantile-quantile plot),一种称为P-P图( probabilit probability plot)。
Q-Q图是根据观测值的实际分位数与理论分布(如正态分布)的分位数的符合程度绘制的,有时也称为分位数-分位数图;P-P图则是根据观测数据的累积概率与理论分布(如正态分布)的累积概率的符合程度绘制的。
下图是用R模拟的几种不同分布的Q-Q图
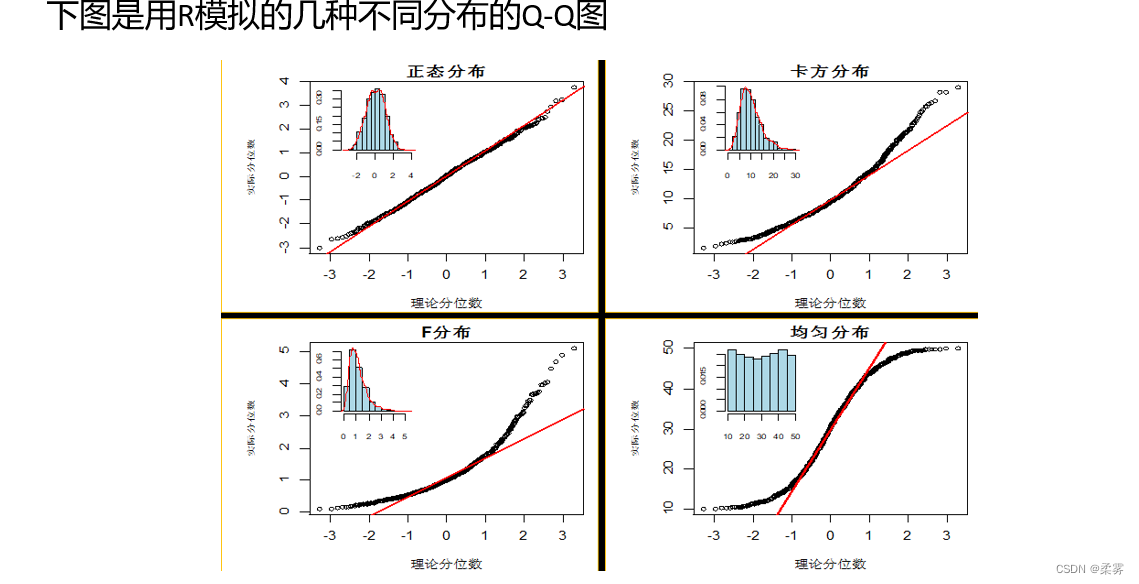
例题:
(数据: example6_3.RData)沿用例6-3。会制Q-Q图和P-P图,检验该城市每立方米空气中的PM2.5是否服从正态分布。
# 绘制Q-Q图qqnorm(x,xlab=" ",ylab=" ",datax=TRUE,main="正态Q-Q图")qqline(x,datax=TRUE,col="")# 绘制P-P图f<-ecdf(x)p1<-f(x)#y<- ecdf(x);y(x);plot(x,y(x), ylab = "ECDF(x)")p2<-pnorm(x,mean(x),sd(x)) plot(p1,p2,xlab="观测的累积概率",ylab="期望的累积概率",main="正态P-P图")abline(a=0,b=1,col=" ")
# 绘制Q-Q图load("C:/example/ch6/example6_3.RData")par(mfrow=c(1,2),cex=0.8,mai=c(0.7,0.7,0.2,0.1))qqnorm(example6_3$PM2.5值,xlab="期望正态值",ylab="观测值",datax=TRUE,main="正态Q-Q图")qqline(example6_3$PM2.5值,datax=TRUE,col="red")# 绘制P-P图f<-ecdf(example6_3$PM2.5值)p1<-f(example6_3$PM2.5值)#y<- ecdf(x);y(x);plot(x,y(x), ylab = "ECDF(x)")p2<-pnorm(example6_3$PM2.5值,mean(example6_3$PM2.5值),sd(example6_3$PM2.5值)) plot(p1,p2,xlab="观测的累积概率",ylab="期望的累积概率",main="正态P-P图")abline(a=0,b=1,col="red")
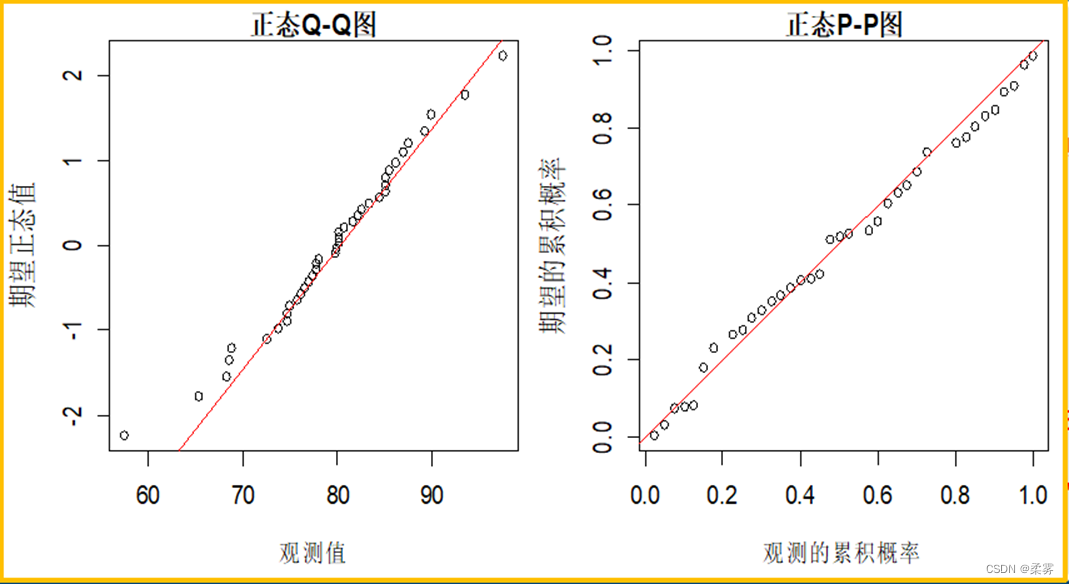
图中的直线表示理论正态分布线,各观测点越靠近直线,且呈随机分布,表示数据越接近正态分布。从图中可以看出,各观测点大致围绕在一条直线周围随机分布,可以说该城市每立方米空气中的PM2.5基本上服从正态分布。
在分析正态概率图时,最好不要用严格的标准去衡量数据点是否在理论直线上,只要各点近似在一条直线周围随机分布即可。而且当样本量比较小时正态概率图中的点很少,提供的正态性信息很有限,因此样本量应尽可能大。
Shapiro-Wilk和K-S正态性检验
当样本量较小时,正态概率图的应用就会受到限制,这时可以使用标准的统计检验方法。检验的原假设是总体服从正态分布。
如果检验获得的P值小于指定的显著性水平,则拒绝原假设,表示总体不服从正态分布;如果P值较大不能拒绝原假设,可以认为总体满足正态分布。正态性的检验方法有很多、这里只介绍两种常用的检验方法,即 Shapiro-Wilk检验和K-S检验。
Shapiro-Wilk检验
Shapiro-Wilk检验是S.Shapiro和M.Wilk于1965年提出的,该检验是用顺序统计量W来检验分布的正态性。 Shapiro-wilk检验的具体步骤如下:
首先,对研究的总体提出如下假设:
H0:总体服从正态分布;H1:总体不服从正态分布
然后,按下列公式计算检验统计量W:


(数据: example6_4.RData) 沿用例6-4。用 Shapiro-wilk方法检验该企业生产的砖的厚度是否服从正态分布( 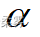 =0.05)。
=0.05)。

load("C:/example/ch6/example6_4.RData")
shapiro.test(example6_4$厚度)

结论:在该项检验中,W=0.91377,P=0.07522,由于P>0.05,不拒绝原假设,没有证据显示该企业生产的砖的厚度不服从正态分布。
K-S检验
Shapiro–Wilk检验只适用于小样本场合(3≤n<50),当样本量较大时,可使用K-S检验。该检验既可以用于大样本,也可以用于小样本。
K-S检验用来检验总体是否服从某个已知的理论分布。该检验是将某一变量的累积分布函数与特定的分布函数进行比较,检验其拟合程度。设总体的累积分布函数为F(x),已知的理论分布函数为F0(x),则检验的原假设和备择假设为:


K-S检验
如果H0成立,每次抽样得到的D值应当不会与0偏离太远,否则就应拒绝H0。对于设定的显著性水平 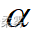 ,若检验统计量D(或z)对应的概率小于
,若检验统计量D(或z)对应的概率小于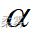 ,则拒绝H0,表示总体与指定的理论分布差异显著。
,则拒绝H0,表示总体与指定的理论分布差异显著。
K-S检验要求样本数据是连续的数值数据,而且要求理论分布已知。比如,要检验的样本数据是否来自μ=100, =10的正态总体,即 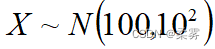 。当总体均值和方差未知时,可以用样本均值 和方差 来代替
。当总体均值和方差未知时,可以用样本均值 和方差 来代替
K-S检验的函数为:ks.test(x,y,…).参数x为向量或数据框;y指定分布,pnom表示要检验的是正态分布;mean和sd是正态分布的均值和标准差。
(数据: example6_4.RData) 沿用例6-4。用K-S方法检验该企业生产的砖的厚度是否服从正态分布( 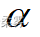 =0.05)。
=0.05)。
ks.test(x,y,…).参数x为向量或数据框;y指定分布;

load("C:/example/ch6/example6_4.RData")
ks.test(example6_4$厚度,"pnorm", mean(example6_4$厚度), sd(example6_4$厚度))

结论:在该项检验中,D=0.23538,P=0.2178,由于P>0.05,不拒绝H0,没有证据显示该企业生产的砖的厚度不服从正态分布。
注:K-S检验的函数为:ks.test(x,y,…).参数x为向量或数据框;y指定分布,pnom表示要检验的是正态分布;mean和sd是正态分布的均值和标准差。
由于 Shapiro-Wilk检验和K-S检验对正态性偏离十分敏感,因此当样本数据轻微偏离正态分布时,这些检验往往也会导致拒绝原假设。当某些分析对正态性的要求相对宽松时,应谨慎使用这些检验。
总体位置参数的检验
总体位置参数的检验是参数检验的一种替代方法。当只有一个总体时,通常关心总体的某个位置参数(如中位数)是否等于假设值,检验方法主要是 Wilcoxon(威尔科克森)符号秩检验。当有两个总体时,通常关心两个总体的位置参数是否相同。对于独立样本,采用Mann- Whitney(曼-惠特尼)检验;对于配对样本,则采用配对样本的 Wilcoxon符号秩检验。
秩(rank)的概念:
秩就是一组数据按照从小到大的顺序排列之后,每一个观测值所在的位置
用一般符号R来表示,假定一组数据  按照从小到大的顺序排列, 在所有观测值中排第
按照从小到大的顺序排列, 在所有观测值中排第 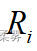 位,那么
位,那么 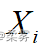 的秩即为
的秩即为 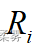 。
。
也是一个统计量,它测度的是数据观测值的相对大小,大多数非参数检验方法正是利用秩的这一性质来排除总体分布未知的障碍的。当然,也有一些非参数方法并不涉及秩的性质。
结(ties)的处理:
很多情况下,数据中会出现相同的观测值,那么对它们进行排序后,这些相同观测值的排名显然是并列的,也就是说它们的秩是相等的,这种情况被称为数据中的“结”
对于结的处理,通常是以它们排序后所处位置的平均值作为它们共同的秩
当一个数据中结比较多时,某些非参数检验中原假设下检验统计量的分布就会受到影响,从而需要对统计量进行修正(一般情况下,软件会自动作出修正)
Wilcoxon符号秩检验(Wilcoxon signed ranks test)是由Frank Wilcoxon于1945年提出的,它是单样本t检验的一种替代方法,用于检验总体中位数是否等于某个假设的值。该检验假定样本数据来自连续对称分布的总体。设总体真实中位数为M,假设的中位数为M0, Wilcoxon符号秩检验的步骤如下:
第1步:提出假设
双侧检验:H0:M=M0,H1:M≠M0;
左侧检验:H0:M=M0,H1:M<M0;
右侧检验:H0:M=M0,H1:M>M0。


例题:
(数据: example6_4.RData) 沿用例6-4。假定样本数据来自连续对称分布总体,但不知道总体的具体分布。检验该企业生产的砖的厚度中位数是否等于5cm( 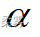 =0.05)
=0.05)

注:函数 wilcox.test(x,…)中,参数m为假定的中位数,alternative=c(“two.side””less”," greater")指定备择假设的方向,默认为alternative="two.side”
load("C:/example/ch6/example6_4.RData")
wilcox.test(example6_4$厚度,m = 5)

注:函数 wilcox.test(x,…)中,参数m为假定的中位数,alternative=c(“two.side””less”," greater")指定备择假设的方向,默认为alternative="two.side”
结论:在该项检验中,统计量V=2,P=0.0005812,由于P<0.05,拒绝H0。有证据显示该企业生产的砖的厚度中位数与5cm有显著差异。
练习
1、(数据: exercise6_2.RData) 安装于一种联合收割机的金属板的平均重量为25千克。对某企业生产的20块全属板进行测量,得到的重量数据如下:
(1)采用 Shapiro-Wik检验方法,检验该企业生产的全属板的重量是否从正态分布( 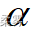 =0.05)
=0.05)
解:提出假设:
H0:该企业生产的全属板的重量服从正态分布;H1:该企业生产的全属板的重量不服从正态分布
load("C:/example/ch6/exercise6_2.RData")
shapiro.test(exercise6_2$重量)

结论:在该项检验中,W=0.97064,P=0.7684,由于P>0.05,不拒绝原假设,没有证据显示该企业生产的金属板的重量不服从正态分布。
(2)假定金属板的重量服从正态分布,检验该企业生产的金属板是否符合要求 ( 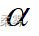 =0.05)
=0.05)
解:提出假设:该企业生产的全属板的平均重量为μ
H0: μ=25;H1:μ 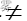 25
25
t.test(exercise6_2$重量,mu=25,conf.level=0.95)

结论:P=0.3114>0.05,不拒绝原假设,没有证据表明该企业生产的金属板的重量不符合要求。
(3)计算效应量,分析差异程度
单样本t检验的效应量:
library(lsr)
cohensD(exercise6_2$重量,mu=25)

结论:0.2<d<0.5 小的效应量
相关文章:

统计学-R语言-7.3
文章目录 前言总体方差的检验一个总体方差的检验两个总体方差比的检验 非参数检验总体分布的检验正态性检验的图示法Shapiro-Wilk和K-S正态性检验总体位置参数的检验 练习 前言 本篇文章继续对总体方差的检验进行介绍。 总体方差的检验 一个总体方差的检验 在生产和生活的许多…...
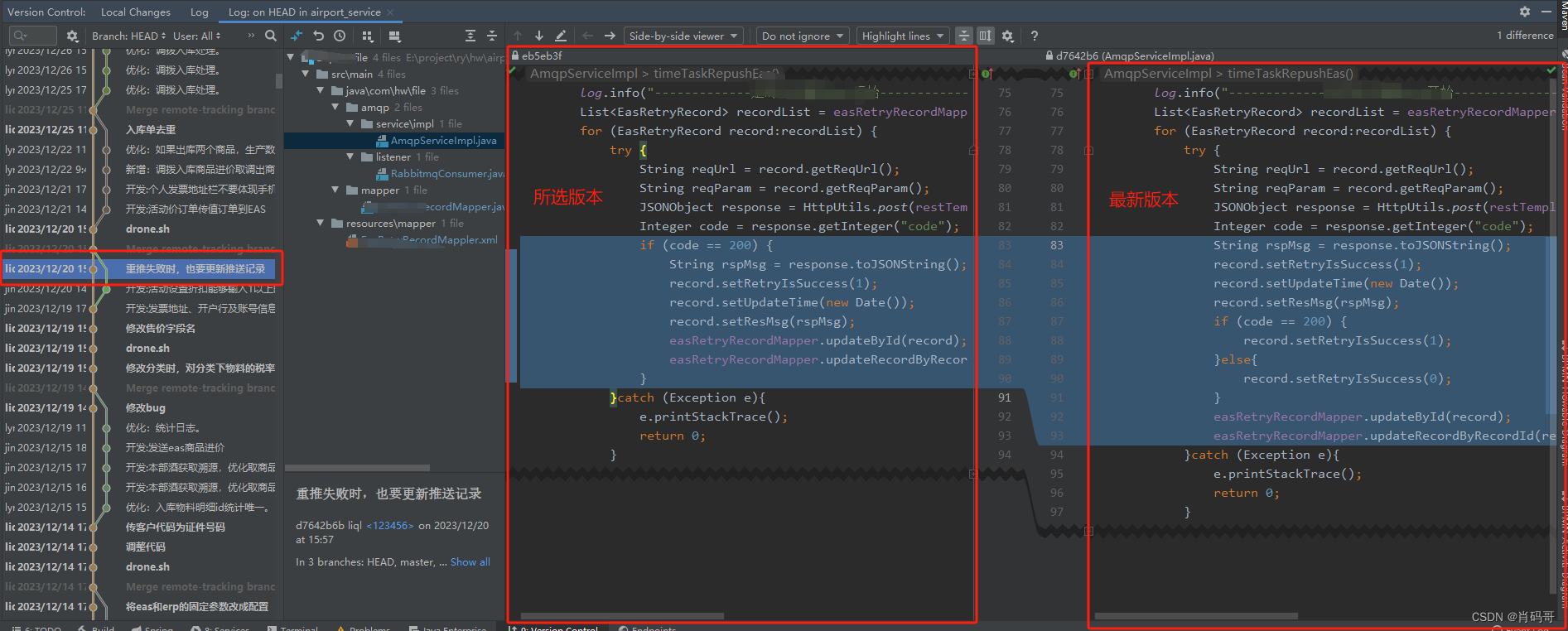
在Idea中使用git查看历史版本
idea查git历史 背景查看步骤总结 背景 有好几次同事到我电脑用idea查看git管理的历史记录,每次都说我的idea看不了历史版本,叫我到他电脑上去看,很晕,为什么,原来是我自己把显示历史文件的视图覆盖了,下面我们来一起学…...

书籍 - 《华杉讲透孙子兵法》 - 11
第十章 地形第十 六种地形的用兵之道(一):先占有利地形 我们读兵法,会发现很多时候,等待都是最好的策略。你一定要懂得等,等得起。有的人不能等,总以为等待就是不作为,那就容易“胡作…...

2024 axios封装 包括请求拦截、错误码等
1.新建 codeMessage.ts export default {200: "服务器成功返回请求的数据。",201: "新建或修改数据成功。",202: "一个请求已经进入后台排队(异步任务)。",204: "删除数据成功。",400: "发出的请求有错误…...

Kotlin Multiplatform项目推荐 | 太空人分布图
Kotlin Multiplatform项目推荐 | 太空人分布图 项目简介 Kotlin Multiplatform项目是一种跨平台开发技术,它可以同时使用SwiftUI、Jetpack Compose、Compose for Wear OS、Compose for Desktop、Compose for Web、Kotlin/JS React等客户端框架,并且使…...
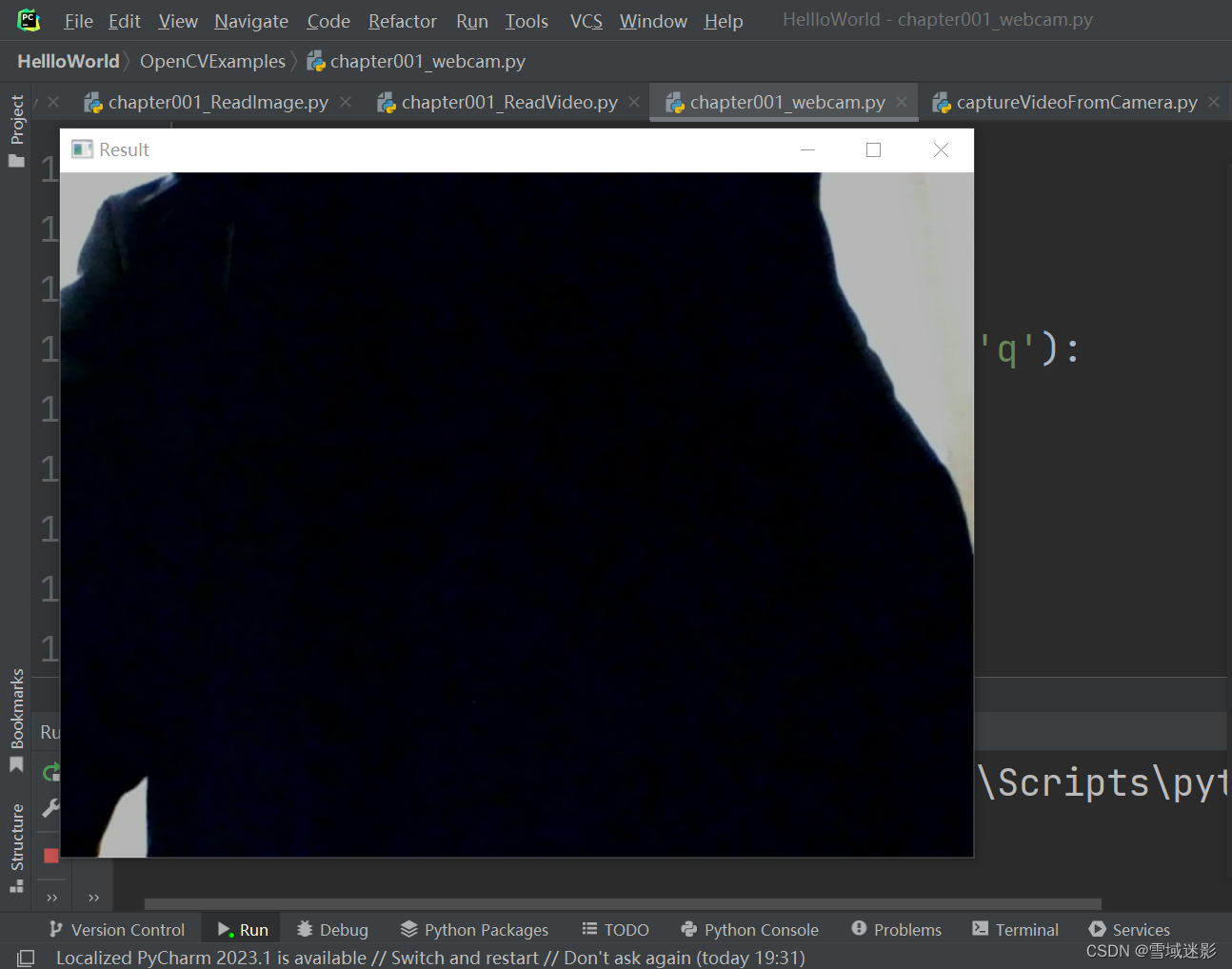
使用Opencv-python库读取图像、本地视频和摄像头实时数据
使用Opencv-python库读取图像、本地视频和摄像头实时数据 Python中使用OpenCV读取图像、本地视频和摄像头数据很简单, 首先需要安装Python,然后安装Opencv-python库 pip install opencv-python然后在PyCharm或者VScode等IDE中输入对应的Python代码 一…...
webpack如何把dist.js中某个模块js打包成一个全局变量,使得在html引入dist.js后可以直接访问
webpack可以通过使用expose-loader来将模块中的一个js文件暴露为全局可以访问的变量。下面是一个示例代码: 1、安装expose-loader npm install expose-loader --save-dev 2、webpack.config.js配置文件 值得注意的是:我在本地使用16.14.2版本的node打包…...
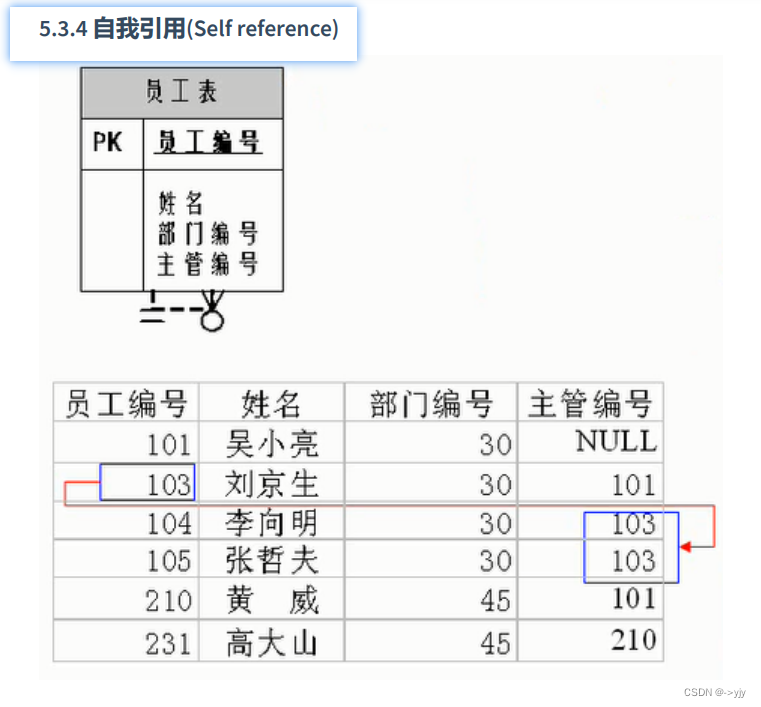
Mysql第一天
数据库概述 1. 为什么要使用数据库 持久化(persistence):把数据保存到可掉电式存储设备中以供之后使用。(可掉电:内存 使用高电压和低电压来区别0和1进行数据的一个存储但是一旦断电了电压都没了 0和1也就没有了)大多数情况下,特别是企 业级应用&#…...

用C语言实现贪吃蛇游戏!!!(破万字)
前言 大家好呀,我是Humble,不知不觉在CSND分享自己学过的C语言知识已经有三个多月了,从开始的C语言常见语法概念说到C语言的数据结构今天用C语言实现贪吃蛇已经有30余篇博客的内容,也希望这些内容可以帮助到各位正在阅读的小伙伴…...
uniapp 使用echarts做折线图条形图。
提前10天把中烟活动做完了,以为能打酱油到除夕那天,结果又要做什么数据看板,方便烟草领导过年查看数据,还只给5天时间,真实压榨剥削啊,下辈子再也不‘拍黄片’了,不!下份工作我就转前…...

美易平台:诺基亚四季度财报超预期
正文: 近日,诺基亚发布了其四季度财报,显示调整后营业利润达到了8.46亿欧元,超出市场预估的7.627亿欧元。同时,调整后每股收益(EPS)为0.10欧元,符合市场预期。这一成绩表明诺基亚在…...
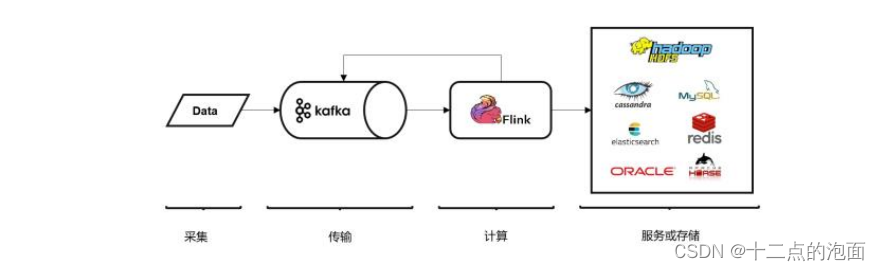
大数据学习之Flink算子、了解(Source)源算子(基础篇二)
Source源算子(基础篇二) 目录 Source源算子(基础篇二) 二、源算子(source) 1. 准备工作 2.从集合中读取数据 可以使用代码中的fromCollection()方法直接读取列表 也可以使用代码中的fromElements()方…...
抖去推短视频矩阵系统+实景无人直播系统技术源头开发
抖去推爆款视频生成器,通过短视频矩阵、无人直播,文案引流等,打造实体商家员工矩阵、用户矩阵、直播矩阵,辅助商家品牌曝光,团购转化等多功能赋能商家拓客引流。 短视频矩阵通俗来讲就是批量剪辑视频和批量发布视频&a…...

【机器学习】一文读懂统计学与机器学习的区别。
统计学与机器学习的区别 1、机器学习2、统计学3、统计学与机器学习异同性3.1 差异性3.2 相似性 4、总结 1、机器学习 关于机器学习,我想大家都很熟悉,这里我再简单唠叨一些 机器学习是人工智能的一个子领域,主要关注如何通过算法使计算机系统…...
燃烧的指针(二)
🌈个人主页:小田爱学编程 🔥 系列专栏:c语言从基础到进阶 🏆🏆关注博主,随时获取更多关于c语言的优质内容!🏆🏆 😀欢迎来到小田代码世界~ &#x…...
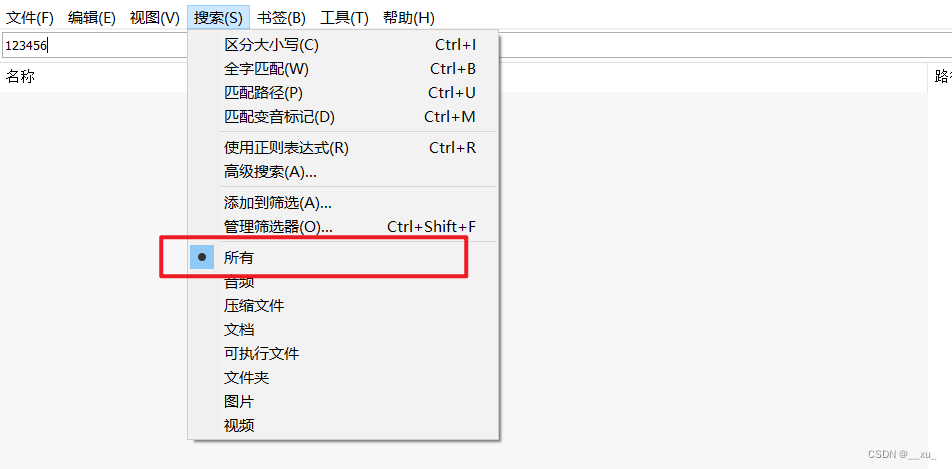
【工具使用-Everything】everything只能搜到文件夹,无法搜到文件
一,问题现象 everything搜索时,只能搜索到文件夹,无法搜索到文件夹下的文件。 二,问题原因 everything搜索设置问题,设置为"文件夹"导致 三,解决方法 将搜索选项设置为“所有”即可&#x…...

手写rpc和redis
rpc框架搭建 consumer 消费者应用 provider 提供的服务 Provider-common 公共类模块 rpc 架构 service-Registration 服务发现 nacos nacos配置中心 load-balancing 负载均衡 redis-trench 手写redis实现和链接 package com.trench.protocol;import com.trench.enumUtil.Redis…...
Unity动画桢事件
1,使用原因 在新项目内部审核的时候,说什么动画节奏不匹配,所以决定用动画桢事件来处理技能释放。当释放技能的时候,先播放技能动画,然后再动画桢所在的时间戳执行技能的逻辑。 2,具体实现 1,…...

搭建Redis集群
一 应用场景 为什么需要redis集群? 当主备复制场景,无法满足主机的单点故障时,需要引入集群配置。 一般数据库要处理的读请求远大于写请求 ,针对这种情况,我们优化数据库可以采用读写分离的策略。我们可以部 署一台…...

C语言sizeof 不是函数吗?
一、问题 sizeof 怎么⽤,它不是函数吗? 二、解答 sizeof 在 C 和 C 中不是一个函数,而是一个运算符。它在编译时计算其操作数所占用的内存大小,并返回一个大小(字节数),这个结果是类型或表达式…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
