数据结构:搜索二叉树 | 红黑树 | 验证是否为红黑树
文章目录
- 1.红黑树的概述
- 2.红黑树的性质
- 3.红黑树的代码实现
- 3.1.红黑树的节点定义
- 3.2.红黑树的插入操作
- 3.3.红黑树是否平衡
黑红树是一颗特殊的搜索二叉树,本文在前文的基础上,图解红黑树插入:前文 链接,完整对部分关键代码展示,完整的代码在gitee仓库中: 链接
文章中有错误的地方,欢迎大家指正!如果有帮助到你,也请多多点赞支持!
1.红黑树的概述
平衡二叉树要求左右子树的高度差的绝对值不超过1,所以平衡二叉树是高度平衡的,正是因为它要求严格控制高度差,在频繁的插入的删除的时候导致旋转次数过多带来了一定的性能消耗!
红黑树也是一颗特殊的搜索二叉树,任何一条从根到叶子的路径上各个结点由颜色(红黑)方式的限制,红黑树确保没有一条路径会比其他路径长出两倍(最长路径不会超过最短路径的两倍),它而是接近平衡的。红黑树没有严格要求高度的平衡,所以红黑树在总体的性能上会略优于平衡二叉树(AVL树)。
在现实的各种应用中都是使用红黑树的来充当数据结构,如:Java集合中的TreeMap,C++STL中Set、Map等都是使用红黑树而不是AVL树。可能在查找方面AVL树会由于红黑树,但是几十次的常数差别,在现代CPU(大概每秒几十亿次)来说完全不受影响,AVL树和红黑树查找的时间复杂度都是在一个等级上O(log_2(N)),红黑树在插入和删除会优于AVL树!
2.红黑树的性质
- 每个结点不是红色就是黑色
- 根节点必须是黑色的
- 如果一个节点是红色的,则它的两个孩子结点必须是是黑色的,(即:不会有两个连续的红节点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点(即:每条路径上黑色的节点相同)
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,即下图的NIL)
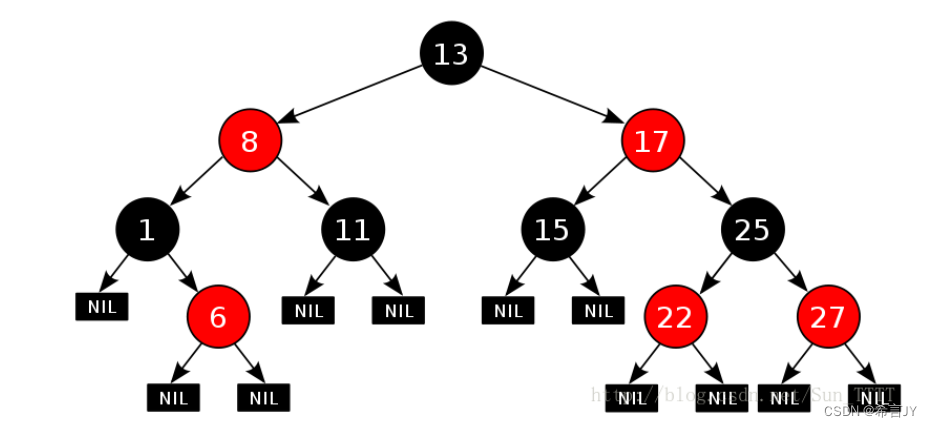
关于路径问题
上图有11条路径
为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍
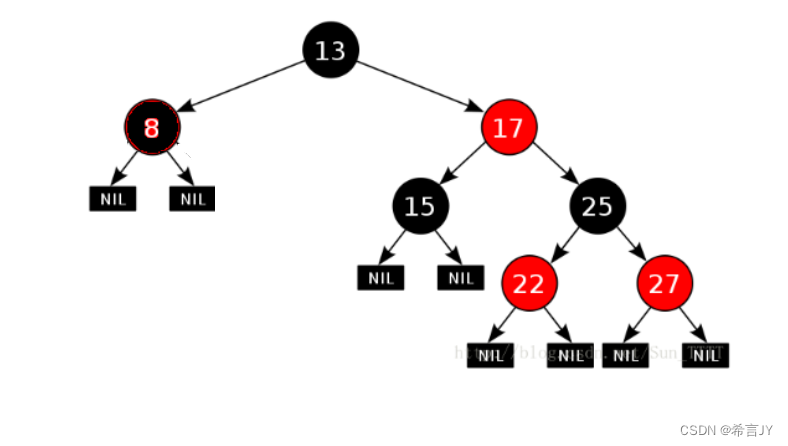
最短路径:全黑的路径 最长路径:一黑一红相间的路径
上面的图情况就是最大的(4个节点/2个节点 = 2倍)的情况!
3.红黑树的代码实现
3.1.红黑树的节点定义
enum color
{RED,BLACK
};template<class K, class V>
struct RBNode
{std::pair<K, V> _kv;RBNode<K, V>* _left;RBNode<K, V>* _right;RBNode<K, V>* _parent;color _color;RBNode(const std::pair<K, V> kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _color(RED){}
};
3.2.红黑树的插入操作
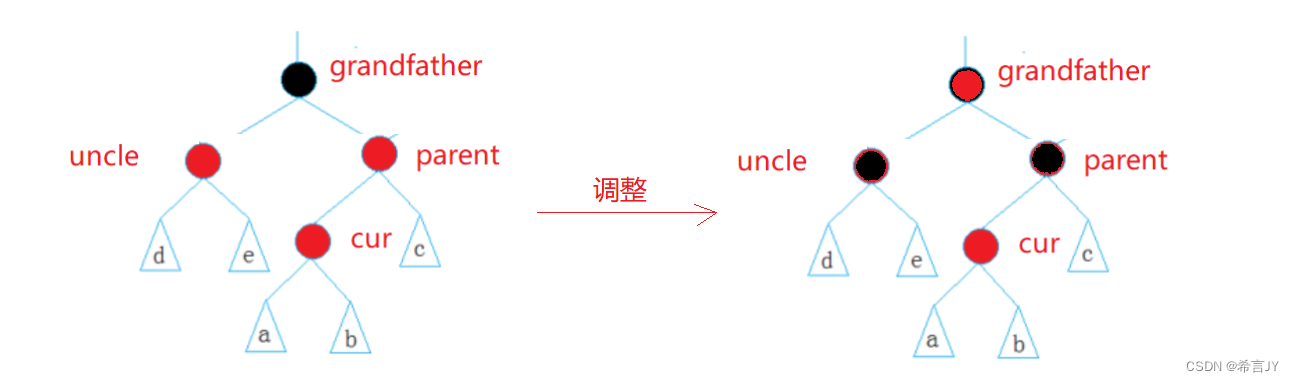
第一大类情况:cur、parent为红,grandfather为黑,uncle存在且为红!

- 将parent和uncle都变为黑,grandfather变为红
- 但是grandfather,如果是根节点直接将其设为黑即可,
- 如果grandfather不为红,如下图:则将cur = grandfather继续重复步骤1和步骤2

**第二大类情况:**cur为红,parent为红,grandfather为黑,uncle不存在或uncle存在且为黑
单旋的情况:
- 下图是uncle不存在或uncle存在且为黑单旋的情况,通过节点的位置判断单旋:如条件是grandfather ->left = parent; parent->left = cur; 直线说明是单旋,都是左边说明右边高,要右单旋!
- 变色,grandfather变为红,parent变为黑色;可以看到,调整后的根据原来的grandfather是黑色,无论往上的祖先是何种颜色,都不会出现两个红色连一起的情况,不用往上调整了!
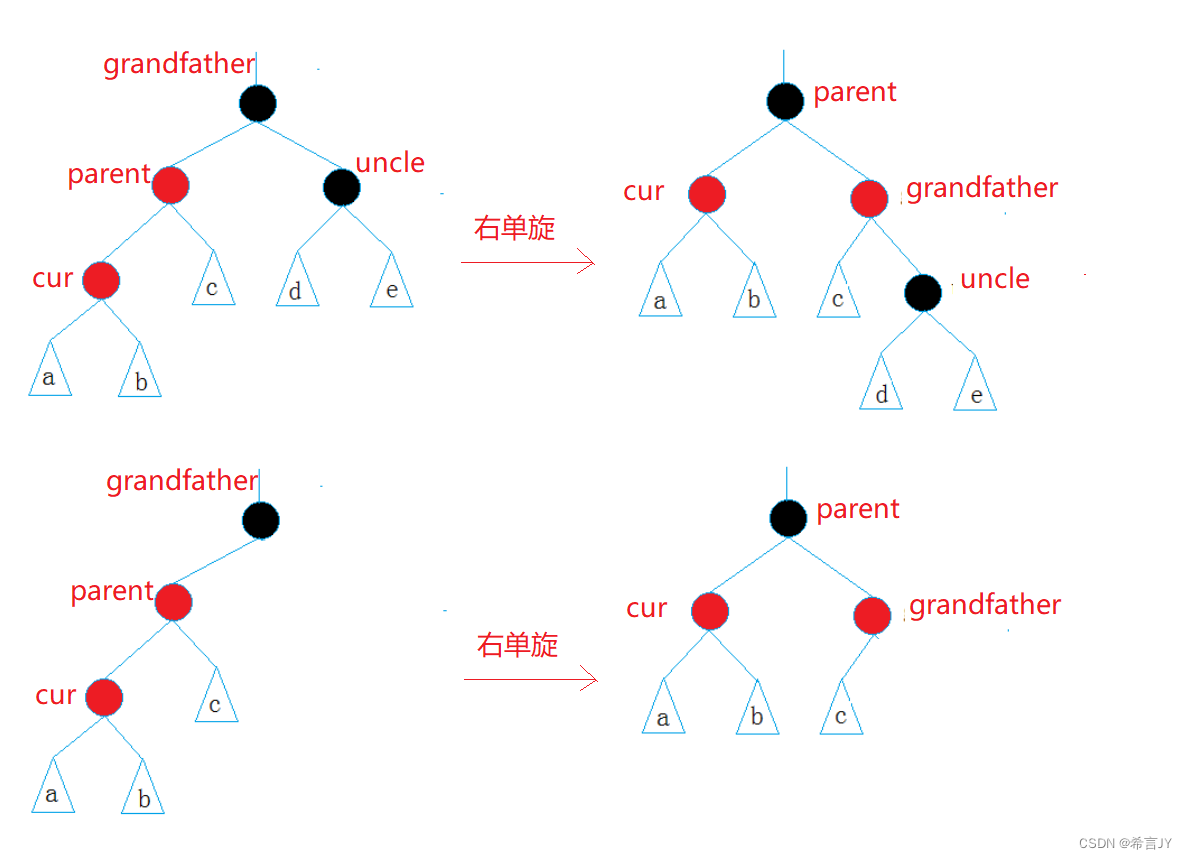
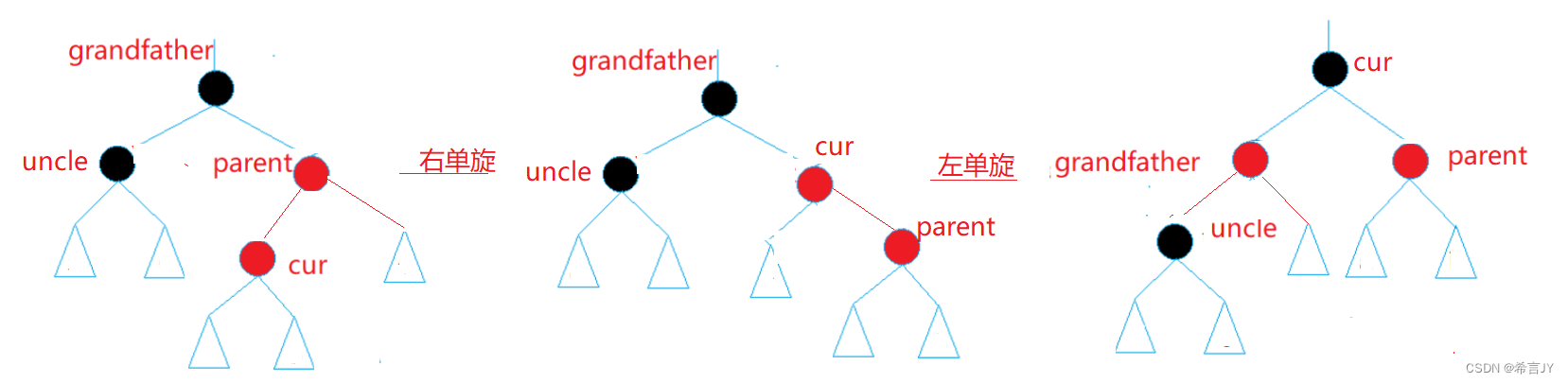
双旋的情况:
- 通过上面的例子可以知道,存在uncle且为黑和不存在uncle的处理结果是一样的!
- 通过下图的判断,是折线:grandfather ->left = parnt;parent->right =cur;通过平衡二叉树的插入操作的学习,可以知道,这种情况先左单旋,再右单旋!
- 变色:grandfather变为红,cur变为黑;可以看到,调整后的根据原来的grandfather是黑色,无论往上的祖先是何种颜色,都不会出现两个红色连一起的情况,不用往上调整了!
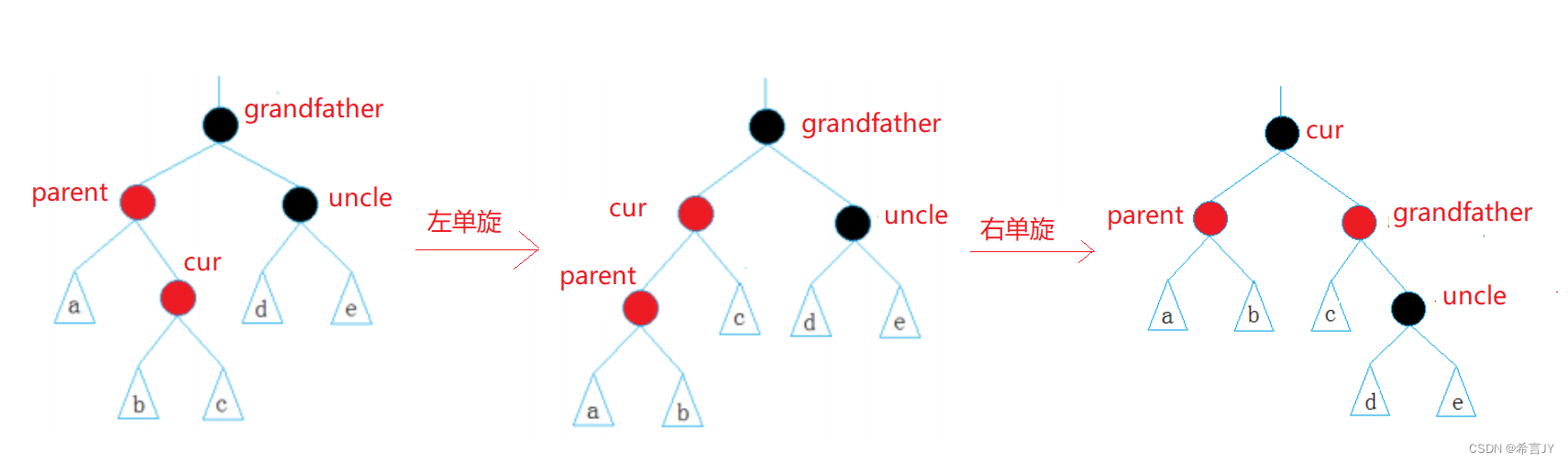
上面就是红黑树的**左子树的插入操作!右子树的插入99%是一样的!**可能没有99%,哈哈哈!但是是类似的操作!简单画个图:
第一大类情况:
第二大类情况:
单旋情况:

双旋情况:
bool insert(const std::pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_color == RED){Node* grandfather = parent->_parent;// parent是左子树if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 第一大类:uncle存在且为红if (uncle && uncle->_color == RED){// 改变颜色parent->_color = uncle->_color = BLACK;grandfather->_color = RED;// 修改条件,继续往上执行cur = grandfather;parent = cur->_parent;}else // 第二大类:uncle不存在或uncle存在且为黑{// 单旋情况if (cur == parent->_left){// 右单旋RotateRight(grandfather);// 改变颜色parent->_color = BLACK;grandfather->_color = RED;}else // 双旋情况{RotateLeft(parent);RotateRight(grandfather);cur->_color = BLACK;grandfather->_color = RED;}// 这种情况就不用重复调整,直接跳出循环break;}}else // parent是右子树{Node* uncle = grandfather->_left;if (uncle && uncle->_color == RED){parent->_color = uncle->_color= BLACK;grandfather->_color = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateLeft(grandfather);parent->_color = BLACK;grandfather->_color = RED;}else{RotateRight(parent);RotateLeft(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break;}}}// 根绝对为黑色_root->_color = BLACK;return true;
}
3.3.红黑树是否平衡
根据每条路径的黑节点的个数相同判断!
bool isBanlan()
{// 如何判断是否为红黑树// 1.高度行不行? 不行! 2.能不能根据节点的个数不操作2倍的关系? 也不行// 3.那有什么是确定的?所有路径黑节点的个数相等!根据这个性质!Node* cur = _root;int checkNum = 0;while (cur){if(cur->_color == BLACK)checkNum++;cur = cur->_left;}return isBanlan(_root,checkNum,0);
}bool isBanlan(Node* root,int &checkNum,int blackNum)
{if (root == nullptr)return true;if (root->_color == BLACK){blackNum++;}if (root->_left == nullptr && root->_right == nullptr){return blackNum == checkNum ? true : false;}bool left = isBanlan(root->_left, checkNum, blackNum);bool right = isBanlan(root->_right, checkNum, blackNum);return left && right;
}
相关文章:

数据结构:搜索二叉树 | 红黑树 | 验证是否为红黑树
文章目录 1.红黑树的概述2.红黑树的性质3.红黑树的代码实现3.1.红黑树的节点定义3.2.红黑树的插入操作3.3.红黑树是否平衡 黑红树是一颗特殊的搜索二叉树,本文在前文的基础上,图解红黑树插入:前文 链接,完整对部分关键代码展示&a…...
数据结构顺序表
思维导图 练习 头文件 1 #ifndef __HEAD_H__2 #define __HEAD_H__3 4 5 #include <stdio.h>6 #include <string.h>7 #include <stdlib.h>8 9 10 #define MAXSIZE 711 typedef int datatype;12 enum13 {14 FLASE-1,15 SUCCESS16 };17 //定义顺序表&a…...
手把手教你优雅的安装虚拟机 Ubuntu —— 图文并茂
目录 Ubuntu 获取Vmware 安装新建虚拟机Ubuntu 安装虚拟机工具安装更多内容 本文教你如何优雅的在虚拟机中安装 Ubuntu,图文并茂、包教包会! Ubuntu 获取 Ubuntu 官网镜像下载速度较慢,建议从国内镜像网站下载,如网易、中科大、…...

源 “MySQL 5.7 Community Server“ 的 GPG 密钥已安装,但是不适用于此软件包。请检查源的公钥 URL 是否配置正确。
源 “MySQL 5.7 Community Server” 的 GPG 密钥已安装,但是不适用于此软件包。请检查源的公钥 URL 是否配置正确。 失败的软件包是:mysql-community-server-5.7.44-1.el7.x86_64 GPG 密钥配置为:file:///etc/pki/rpm-gpg/RPM-GPG-KEY-mysql…...

springboot核心有几层架构
Spring Boot核心有四层架构: 应用层:包含应用程序的入口点和控制器层。这层负责接收请求、处理业务逻辑,并返回响应结果。 服务层:包含业务逻辑的实现。这层负责处理各种业务逻辑,例如数据处理、事务管理等。 数据访…...
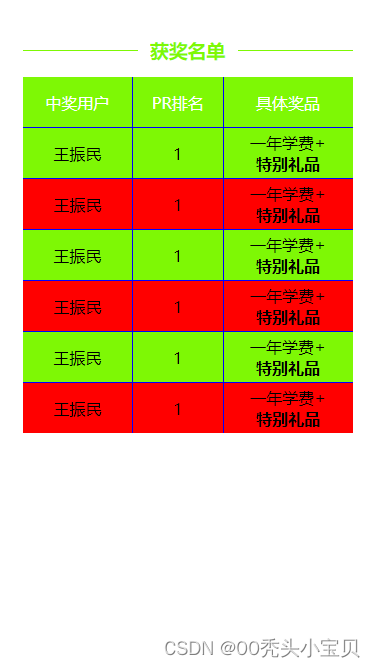
css3表格练习
1.效果图 2.html <div class"line"></div><h3>获奖名单</h3><!-- 表格 cellspacing内边距 cellpadding外边距--><table cellspacing"0" cellpadding"0" ><!-- thead表头 --><thead><tr>…...
项目实战——Qt实现FFmpeg音视频转码器
文章目录 前言一、移植 FFmpeg 相关文件二、绘制 ui 界面三、实现简单的转码四、功能优化1、控件布局及美化2、缩放界面3、实现拖拽4、解析文件5、开启独立线程6、开启定时器7、最终运行效果 五、附录六、资源自取 前言 本文记录使用 Qt 实现 FFmepg 音视频转码器项目的开发过…...

AI数字人-数字人视频创作数字人直播效果媲美真人
在科技的不断革新下,数字人技术正日益融入到人们的生活中。近年来,随着AI技术的进一步发展,数字人视频创作领域出现了一种新的创新方式——AI数字人。数字人视频通过AI算法生成虚拟主播,其外貌、动作、语音等方面可与真实人类媲美…...
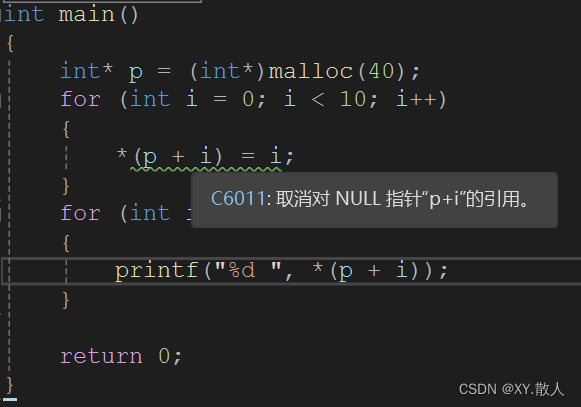
初识C语言·动态内存开辟
1 为什么要有动态内存开辟 int a 10; int arr[10] { 0 }; 上述定义了一个整型,开辟了4个字节,定义了一个整型数组,开辟了40个字节,但是是固定开辟的,面对灵活多变的实际问题的时候可能就有点鸡肋,这种开…...
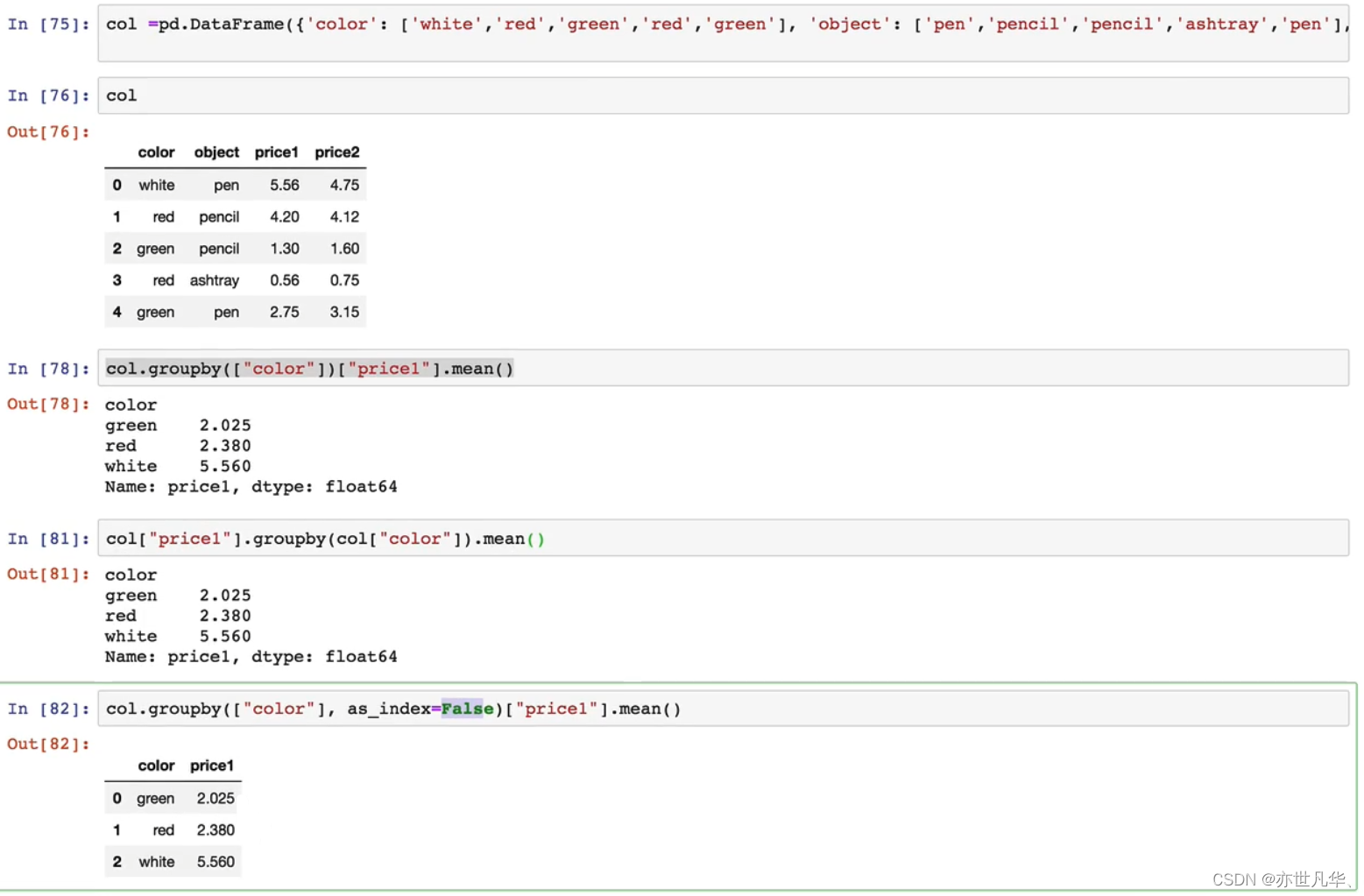
机器学习 | 利用Pandas进入高级数据分析领域
目录 初识Pandas Pandas数据结构 基本数据操作 DataFrame运算 文件读取与存储 高级数据处理 初识Pandas Pandas是2008年WesMcKinney开发出的库,专门用于数据挖掘的开源python库,以Numpy为基础,借力Numpy模块在计算方面性能高的优势&am…...

三、计算机理论-计算机网络-物理层,数据通信的理论基础,物理传输媒体、编码与传输技术及传输系统
物理层概述 物理层为数据链路层提供了一条在物理的传输媒体上传送和接受比特流的能力。物理层提供信道的物理连接,主要任务可以描述为确定与传输媒体的接口有关的一些特性:机械特性、电气特性、功能特性、过程特性 数据通信的理论基础 数据通信的意义 主…...
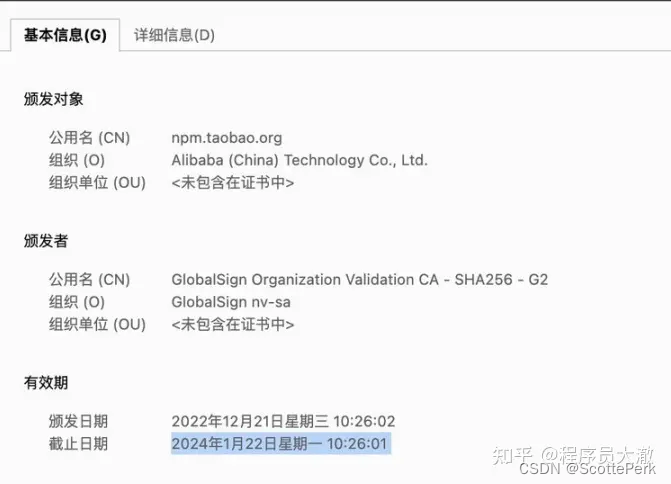
ERROR Failed to get response from https://registry.npm.taobao.org/ 错误的解决
这个问题最近才出现的。可能跟淘宝镜像的证书到期有关。 解决方式一:更新淘宝镜像(本人测试无效,但建议尝试) 虽然无效,但感觉是有很大关系的。还是设置一下比较好。 淘宝镜像的地址(registry.npm.taobao…...

overflow产生的滚动条样式设置
修改overflow产生的滚动条样式,主要可以通过如下三个伪元素设置: 1)-webkit-scrollbar:设置水平滚动条的高度,垂直滚动的宽度 2)-webkit-scrollbar-thumb:设置滚动条里面的滑块样式 3)-webkit-scrollbar-track&…...

Ubuntu环境vscode配置Log4cplus库
1、下载源码 http://sourceforge.net/projects/log4cplus/ 2、安装 例如我下载的是2.0.8版本压缩包,需要解压缩 log4cplus-2.0.8.7z安装解压工具: apt install p7zip-full解压: 7z x log4cplus-2.0.8.7z -r -o/home/配置及编译安装&#x…...

vue中,使用file-saver导出文件,下载Excel文件、下载图片、下载文本
vue中,使用file-saver导出文件,下载Excel文件、下载图片、下载文本 1、基本介绍 npm地址:file-saver - npm 2、安装 # Basic Node.JS installation npm install file-saver --save bower install file-saver# Additional typescript defin…...
)
【VUE】v-if 和 v-show 大详解(多角度分析+面试简答版)
多角度分析+面试简答版 一、`v-if` 和 `v-show` 的区别之多角度分析控制手段:编译过程:编译条件:性能消耗:总结使用场景二、 `v-if`、`v-show`、`display:none` 和`visibility: hidden` 的区别三、简洁版回答:`v-show` 与 `v-if` 比较一、v-if 和 v-show 的区别之多角度分…...

mac intel jdk安装与配置
jdk地址下载 https://www.oracle.com/java/technologies/downloads/ https://repo.huaweicloud.com/java/jdk/8u201-b09/ 安装后 下载完成之后打开终端 注意如果是第一次配置环境变量需要创建.bash_profile文件。(注意:touch后面有空格) to…...
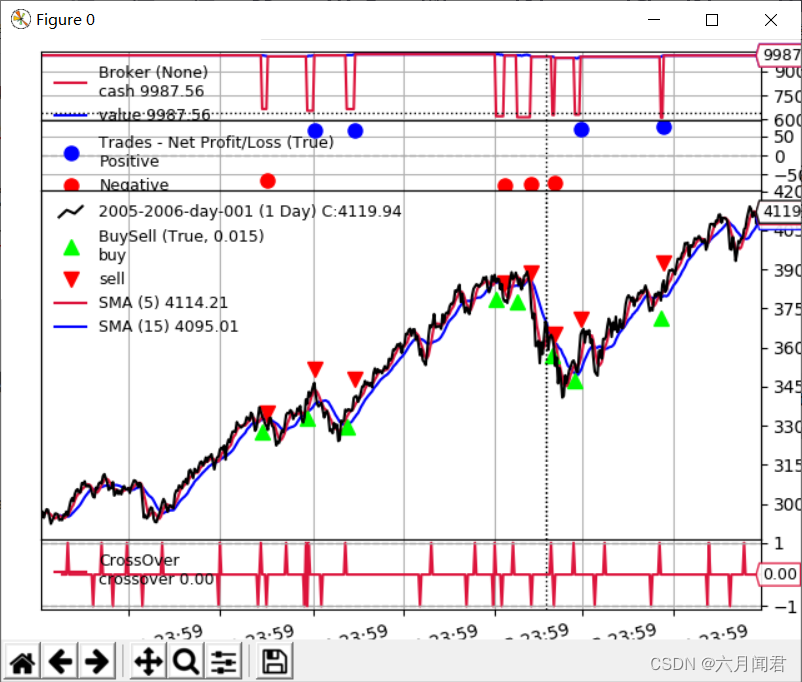
Backtrader 文档学习-Bracket Orders
Backtrader 文档学习-Bracket Orders 1. 概述 组合订单类型是一个非常宽泛的订单类别,只要brokder支持的订单类型都可以, 包括(Market, Limit, Close, Stop, StopLimit, StopTrail, StopTrailLimit, OCO)。 该功能用于回测,交互broker Brac…...
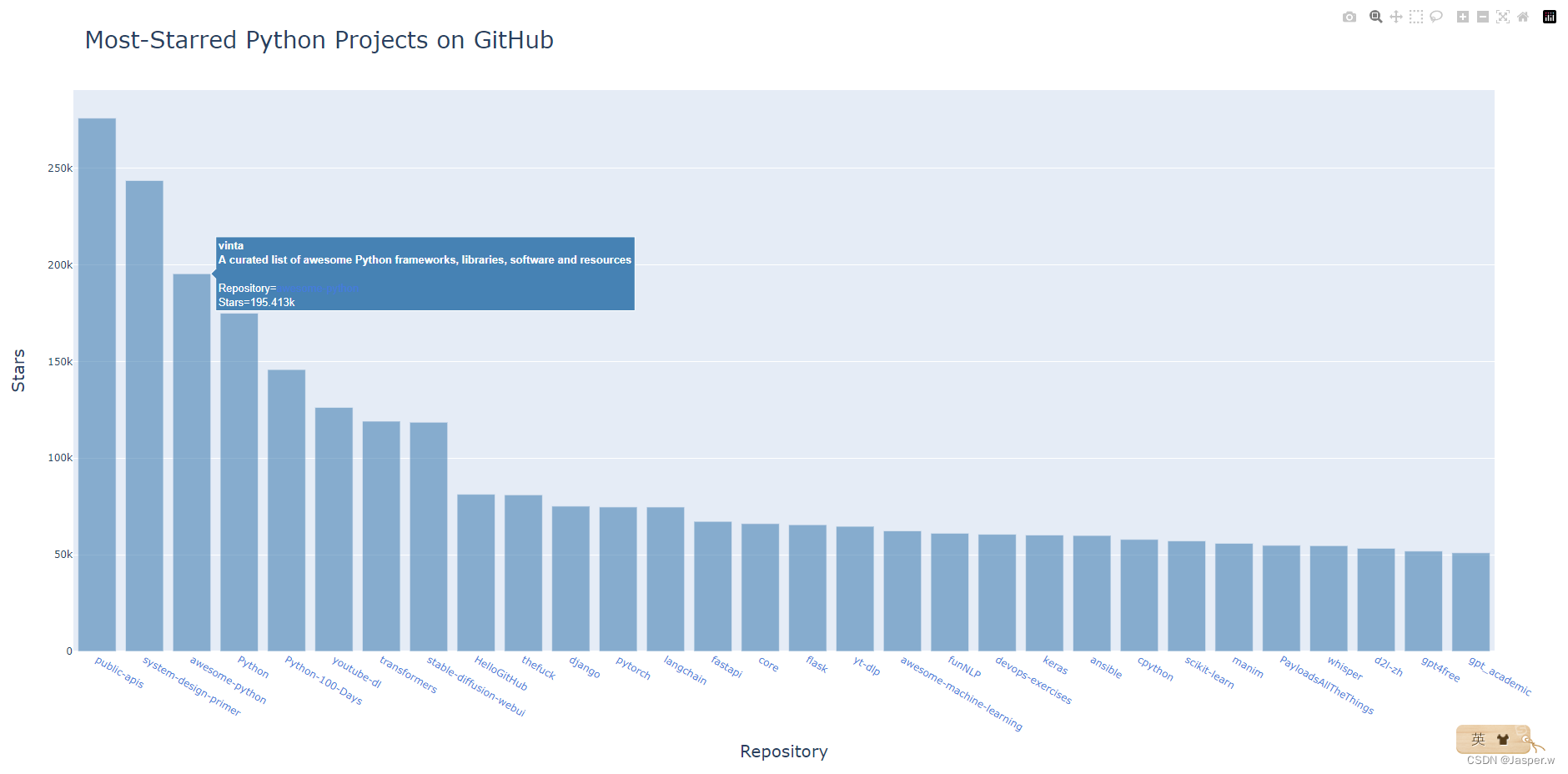
Python编程 从入门到实践(项目二:数据可视化)
本篇为实践项目二:数据可视化。 配合文章python编程入门学习,代码附文末。 项目二:数据可视化 1.生成数据1.1 安装Matplotlib1.2 绘制简单的折线图1.2.1 修改标签文字和线条粗细1.2.2 校正图形1.2.3 使用内置样式1.2.4 使用scatter()绘制散点…...
Linux版本下载Centos操作
目录 一、Centos7 二、下载Centos7镜像 三、下载Centos7 买了个硬件安装裸机(一堆硬件) 把安装盘放到虚拟机里面,给机器加电 配置设置 编辑 网络配置 开启网络功能 四、安装linux客户端 Xshell是什么 Xshell使用(连接…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
