主成分分析(PCA)Python
实际问题研究中,常常遇到多变量问题,变量越多,问题往往越复杂,且各个变量之间往往有联系。于是,我们想到能不能用较少的新变量代替原本较多的旧变量,且使这些较少的新变量尽可能多地保留原来变量所反映的信息。
比如说一件上衣,有身长、袖长、胸围、腰围等等十多个指标,将型号分这么多很麻烦,因此,厂家将十多项指标综合成3项指标,分别反映长度、胖瘦、特殊体型。
变量具有相关性,同时就意味着反映的信息有重叠性,主成分分析就是将重复的变量(关系紧密的变量)删去,建立尽可能少的、互相无关的新变量。
设法将原来变量重新组合成一组新的互相无关的几个综合变量,同时根据实际需要从中取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析法,也是数学上用来降维的一种方法。
通过PCA将n维原始特征映射到k维上(k<n),称这k维为主成分。
找新的维度实质上要使数据间的方差够大,即在新维度下坐标点足够分散、数据间有区分。本质上也就是在做基变换。
下图是一个例子,将5个点降维到一条直线上。
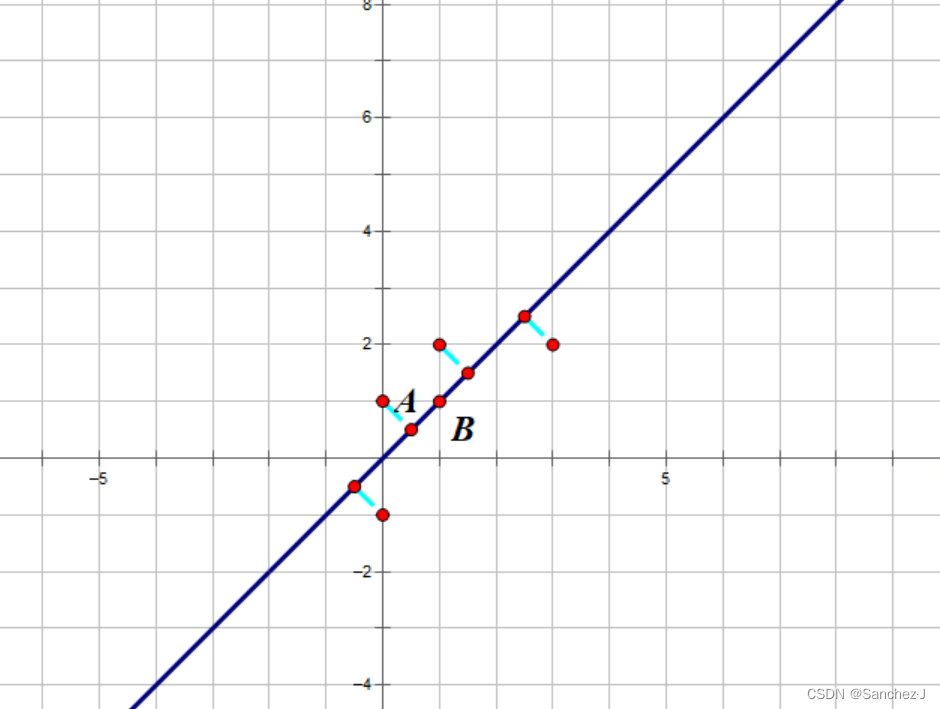
代数上,可以理解为m × n的原始样本X,与n×k阶的矩阵W做矩阵乘法,得到m×k阶低维矩阵Y。
分析思想
假设有n个样板,p个指标,则可以构成大小为n×p的样本矩阵X:
假设我们想找到新的一组变量,其满足
系数确定原则:
与
(
) 线性无关
是
线性组合中方差第k大者,称原变量指标的第k主成分
PCA计算步骤
- 标准化处理
- 计算标准化样本的协方差矩阵
- 计算R的特征值和特征向量(特征值从大到小排序)
- 计算主成分贡献率以及累计贡献率
- 贡献率
- 累计贡献率
- 写出主成分:一般取累计贡献率超过80%的特征值所对应的第1,2,...,m个主成分。其中第 i 个是
(
是第i个特征向量)
- 根据系数分析主成分代表的意义
Python代码
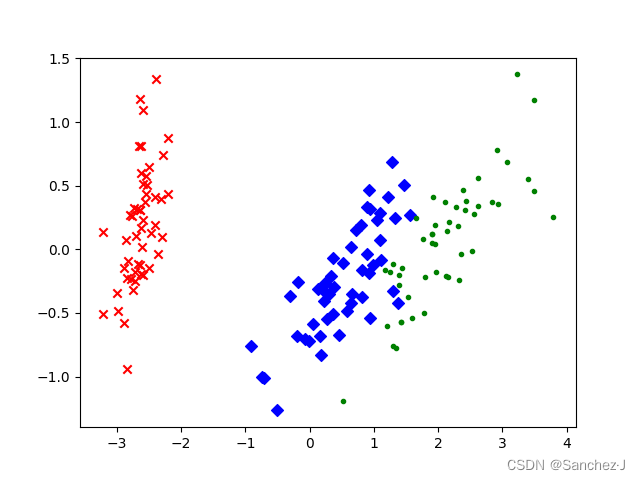
这段代码将Iris数据集降维到二维空间,并使用散点图展示不同类别的鸢尾花在降维后的空间中的分布情况。详见注释。
import matplotlib.pyplot as plt # 加载matplotlib用于数据的可视化
from sklearn.decomposition import PCA # 加载PCA算法包
from sklearn.datasets import load_iris # 从sklearn库中导入load_iris函数,用于加载Iris数据集。data = load_iris() # 使用load_iris函数加载Iris数据集。
y = data.target # 提取数据集的标签(目标变量),表示不同种类的鸢尾花。
x = data.data # 提取数据集的特征,表示鸢尾花的四个特征。
pca = PCA(n_components=2) # 加载PCA算法,设置降维后主成分数目为2
reduced_x = pca.fit_transform(x) # 对原始数据进行PCA降维,将数据转换为新的二维空间。
red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []
# 初始化三个颜色类别(红色、蓝色、绿色)的坐标列表。
for i in range(len(reduced_x)): # 遍历降维后的数据if y[i] == 0: # 如果数据点属于第一类鸢尾花。red_x.append(reduced_x[i][0])red_y.append(reduced_x[i][1])# 将该点在降维后的第一个主成分的坐标添加到红色类别的x坐标列表中。# 将该点在降维后的第二个主成分的坐标添加到红色类别的y坐标列表中。elif y[i] == 1:blue_x.append(reduced_x[i][0])blue_y.append(reduced_x[i][1])else:green_x.append(reduced_x[i][0])green_y.append(reduced_x[i][1])
# 可视化
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()结果
相关文章:

主成分分析(PCA)Python
实际问题研究中,常常遇到多变量问题,变量越多,问题往往越复杂,且各个变量之间往往有联系。于是,我们想到能不能用较少的新变量代替原本较多的旧变量,且使这些较少的新变量尽可能多地保留原来变量所反映的信…...
Leetcode—144. 二叉树的前序遍历【简单】
2023每日刷题(九十六) Leetcode—144. 二叉树的前序遍历 实现代码 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr…...
混淆矩阵、准确率、查准率、查全率、DSC、IoU、敏感度的计算
1.背景介绍 在训练的模型的时候,需要评价模型的好坏,就涉及到混淆矩阵、准确率、查准率、查全率、DSC、IoU、敏感度的计算。 2、混淆矩阵的概念 所谓的混淆矩阵如下表所示: TP:真正类,真的正例被预测为正例 FN:假负类…...

ChatGPT目前的AI一哥
ChatGPT和文心一言是两个不同的AI助手,各自有其独特的特点和应用场景。以下是对它们在智能回复、语言准确性和知识库丰富度等方面的简要比较: 智能回复:ChatGPT是由OpenAI开发的语言模型,具有强大的自然语言处理和生成能力&#x…...

认识思维之熵
经常有读者问我,说: 为什么向您请教一个问题,您总能很快指出在哪篇文章里面提到过,是因为您的记忆力特别好吗? 其实不是的。更重要的原因是:如果你经过系统训练,有意识地去获取知识的话&#x…...

蓝桥杯备战——1.点亮LED灯
1.解析原理图 由上图可以看到8个共阳LED灯接到了573输出口,而573输入接到单片机P0口上。当573 LE脚输入高电平时,输出随输入变化,当LE为低电平时,输出锁存。 由上图可以看到Y4C接到了或非门74HC02的输出端,而输入端为…...

【网络协议测试】畸形数据包——圣诞树攻击(DOS攻击)
简介 TCP所有标志位被设置为1的数据包被称为圣诞树数据包(XMas Tree packet),之所以叫这个名是因为这些标志位就像圣诞树上灯一样全部被点亮。 标志位介绍 TCP报文格式: 控制标志(Control Bits)共6个bi…...

Java基础面试题-5day
泛型 什么是泛型?有什么用? 泛型是jdk5引入的新特性,通过泛型可以提高代码的可读性和稳定性;当我们使用泛型时,传入的对象类型必须是指定的泛型类型,否则就会报错 泛型的使用方式有哪些? 一…...

软通智慧启动鲲鹏原生应用开发合作
1月25日,软通智慧科技有限公司启动鲲鹏原生应用开发合作,将基于鲲鹏硬件底座、openEuler、开发套件Kunpeng DevKit和应用使能套件Kunpeng BoostKit开展面向智慧园区、政务、水利水务等行业场景的软硬件原生应用开发,并持续发布性能更优的鲲鹏…...
【STM32】STM32F4中USB的CDC虚拟串口(VCP)使用方法
文章目录 一、前言二、STM32CubeMX生成代码2.1 选择芯片2.2 配置相关模式2.3 设置时钟频率2.4 生成代码2.5 编译并下载代码2.6 结果2.7 问题 三、回环测试3.1 打开工程3.2 添加回环代码3.3 编译烧录并测试 四、出现问题和解决方法4.1 烧录总是要自己插拔USB4.2 自己生成的工程没…...
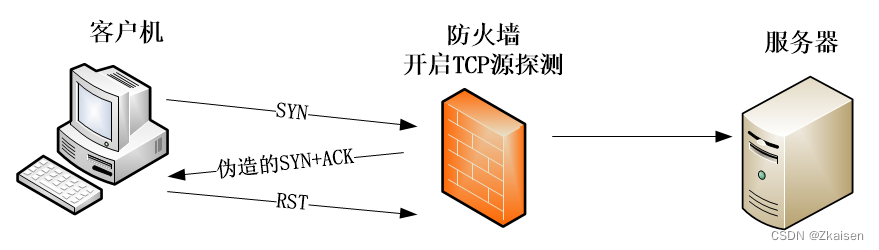
网络协议与攻击模拟_06攻击模拟SYN Flood
一、SYN Flood原理 在TCP三次握手过程中, 客户端发送一个SYN包给服务器服务端接收到SYN包后,会回复SYNACK包给客户端,然后等待客户端回复ACK包。但此时客户端并不会回复ACK包,所以服务端就只能一直等待直到超时。服务端超时后会…...
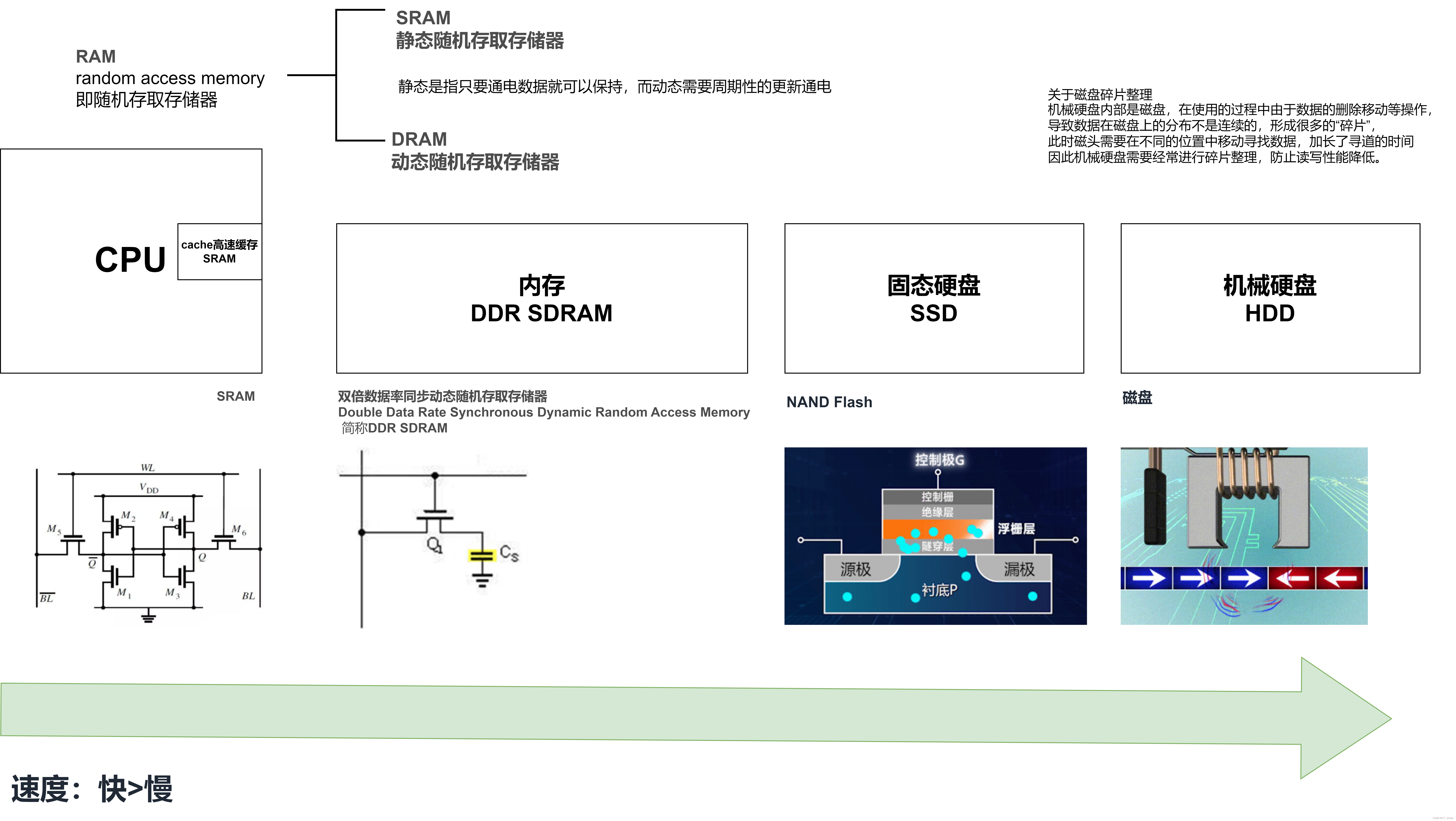
CPU,内存和硬盘之间的关系
计算机三大件:CPU,内存,硬盘。从运算速度来看,CPU>内存>固态硬盘>机械硬盘。 电脑卡顿怎么解决? 1、清理垃圾; 2、释放C盘空间,因为系统需要C盘空间当作虚拟内存; 3、增…...
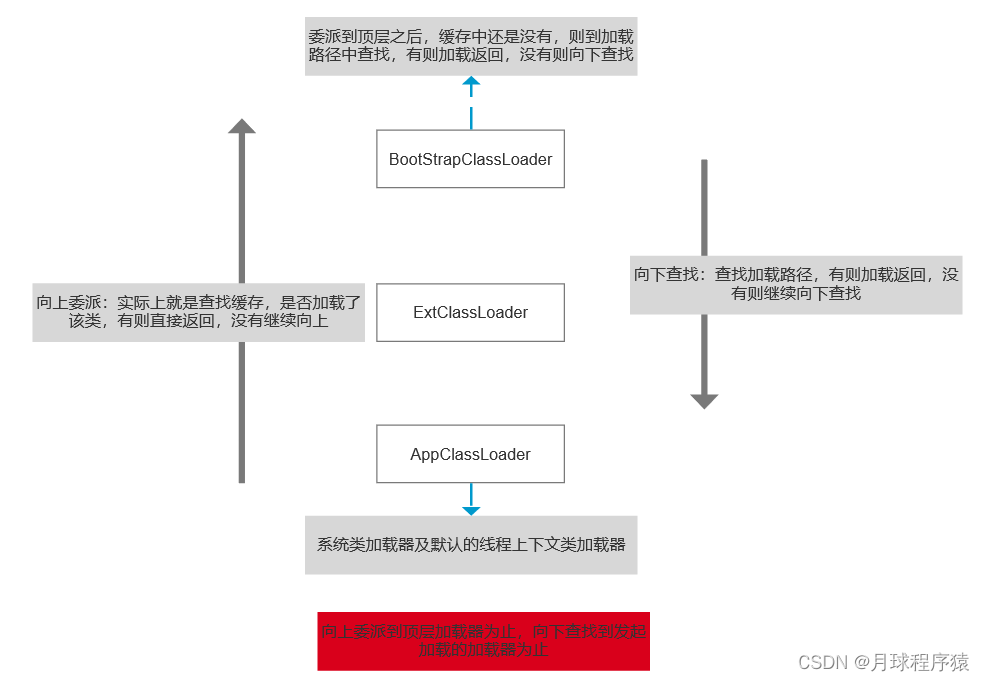
Java面试题之基础篇
文章目录 一:谈谈你对面向对象的理解二:JDK、JRE、JVM三者区别和联系三:和equals比较四:hashCode与equals五:final六:String、StringBuffer、StringBuilder七:重载与重写的区别?八&a…...
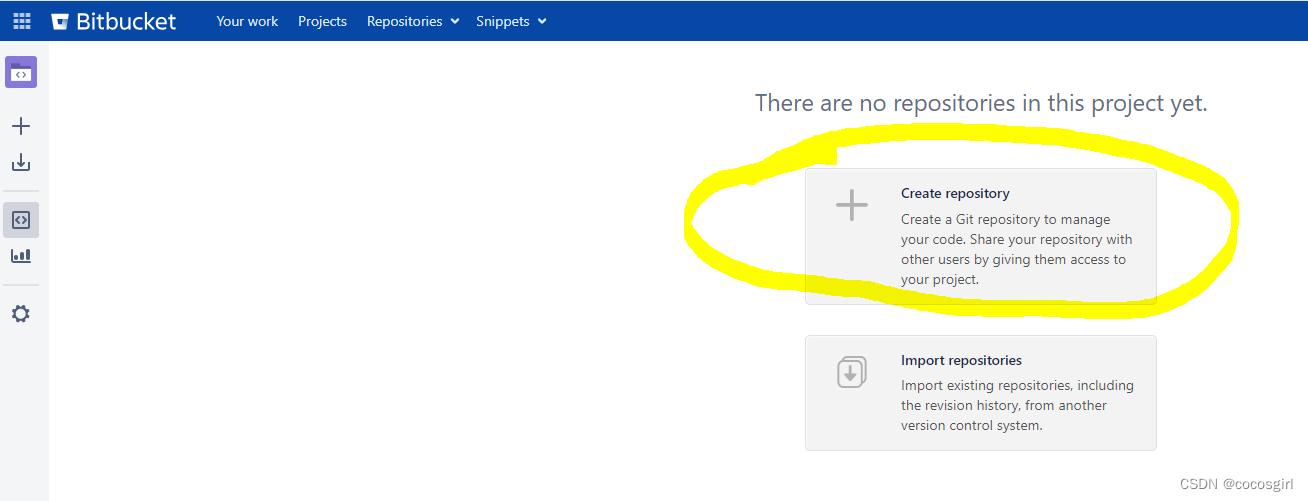
Bitbucket第一次代码仓库创建/提交/创建新分支/合并分支/忽略ignore
1. 首先要在bitbucket上创建一个项目,这个我没有权限创建,是找的管理员创建的。 管理员创建之后,这个项目给了我权限,我就可以创建我的代码仓库了。 2. 点击这个Projects下的具体项目名字,就会进入这样一个页面&#…...

c#反射用法
在 C# 中,反射是一种能够在运行时检查类型信息、访问属性和调用方法的机制。通过反射,你可以动态地操作类型、对象和程序集,而无需在编译时知道这些类型的具体信息。 反射提供了一组 API,可以让你在运行时获取和操作类型的信息。…...

WPF行为
背景:实现按钮鼠标移动到上方有点交互效果或变一下有阴影。这样使用触发器就行了,但是如果是每个控件都有效果的话使用行为更加合适 1、下载NuGet包:Microsoft.xaml.behavior.wpf 2、创建行为类EffectBehavior,对Behavior进行重写…...
N-141基于springboot,vue网上拍卖平台
开发工具:IDEA 服务器:Tomcat9.0, jdk1.8 项目构建:maven 数据库:mysql5.7 系统分前后台,项目采用前后端分离 前端技术:vueelementUI 服务端技术:springbootmybatis-plusredi…...

Unity之Cinemachine教程
前言 Cinemachine是Unity引擎的一个高级相机系统,旨在简化和改善游戏中的相机管理。Cinemachine提供了一组强大而灵活的工具,可用于创建令人印象深刻的视觉效果,使开发人员能够更轻松地掌控游戏中的摄像机行为。 主要功能和特性包括&#x…...
)
java面面试面经(面试过程)
一、校招一面面经 1.1 自我介绍(2min) 1.2 要求介绍项目一项目亮点以及做的具体工作 根据介绍项目进行细挖,其中包括方案设计、场景设计等等等 由于项目一种涉及数据库源的转换问题和限流方案,所以面试官拷打的是这两块,其中包括场景题&…...

大语言模型-大模型基础文献
大模型基础 1、Attention Is All You Need https://arxiv.org/abs/1706.03762 attention is all you need 2、Sequence to Sequence Learning with Neural Networks https://arxiv.org/abs/1409.3215 基于深度神经网络(DNN)的序列到序列学习方法 3、…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
