第2章-神经网络的数学基础——python深度学习
第2章 神经网络的数学基础
2.1 初识神经网络
关于类和标签的说明

from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()# 代码清单 2-1 加载keras中的minst数据集
from keras.datasets import mnist
from keras.utils import to_categorical(train_images, train_labels), (test_images, test_labels) = mnist.load_data()print('train_images.shape:', train_images.shape)
print('len(train_labels)', len(train_labels))print('train_labels', train_labels)print('test_images.shape:', test_images.shape)
print(' len(test_labels):', len(test_labels))
print('test_labels:', test_labels)
运行结果:
train_images.shape: (60000, 28, 28)
len(train_labels) 60000
train_labels [5 0 4 ... 5 6 8]
test_images.shape: (10000, 28, 28)len(test_labels): 10000
test_labels: [7 2 1 ... 4 5 6]# 代码清单 2-2 网络架构
from keras import models
from keras import layersnetwork = models.Sequential()
# Dense 也就是全连接的神经网络
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))# 2.3 编译步骤
# 编译的三个参数:损失函数、优化器、监控的指标(精度)
network.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy'])# 2-4 准备图像数据
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255# 2-5准备标签
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)network.fit(train_images, train_labels, epochs=5, batch_size=128)test_loss, test_acc = network.evaluate(test_images, test_labels)
print('test_acc:', test_acc)469/469 [==============================] - 1s 2ms/step - loss: 0.2649 - accuracy: 0.9234
Epoch 2/5
469/469 [==============================] - 1s 2ms/step - loss: 0.1077 - accuracy: 0.9678
Epoch 3/5
469/469 [==============================] - 1s 2ms/step - loss: 0.0712 - accuracy: 0.9790
Epoch 4/5
469/469 [==============================] - 1s 2ms/step - loss: 0.0508 - accuracy: 0.9847
Epoch 5/5
469/469 [==============================] - 1s 2ms/step - loss: 0.0380 - accuracy: 0.9885
313/313 [==============================] - 0s 923us/step - loss: 0.0592 - accuracy: 0.9812
test_acc: 0.98119997978210452.2 神经网络的数据表示
前面例子使用的数据存储在多维 Numpy 数组中,也叫张量(tensor)。一般来说,当前所有机器学习系统都使用张量作为基本数据结构。张量对这个领域非常重要,重要到 Google 的TensorFlow 都以它来命名。
张量这一概念的核心在于,它是一个数据容器。它包含的数据几乎总是数值数据,因此它是数字的容器。你可能对矩阵很熟悉,它是二维张量。张量是矩阵向任意维度的推广[注意,张量的维度(dimension)通常叫作轴(axis)]。
2.2.1 标量(0D 张量)
仅包含一个数字的张量叫作标量(scalar,也叫标量张量、零维张量、0D 张量)。在 Numpy中,一个 float32 或 float64 的数字就是一个标量张量(或标量数组)。你可以用 ndim 属性来查看一个 Numpy 张量的轴的个数。标量张量有 0 个轴(ndim == 0)。张量轴的个数也叫作阶(rank)。下面是一个 Numpy 标量。
>>> import numpy as np
>>> x = np.array(12)
>>> x
array(12)
>>> x.ndim
02.2.2 向量(1D 张量)
数字组成的数组叫作向量(vector)或一维张量(1D 张量)。一维张量只有一个轴。下面是
一个 Numpy 向量。
>>> x = np.array([12, 3, 6, 14, 7])
>>> x
array([12, 3, 6, 14, 7])
>>> x.ndim
1这个向量有 5 个元素,所以被称为 5D 向量。
不要把 5D 向量和 5D 张量弄混!
5D 向量只有一个轴,沿着轴有 5 个维度,而 5D 张量有 5 个轴(沿着每个轴可能有任意个维度)。
维度(dimensionality)可以表示沿着某个轴上的元素个数(比如 5D 向量),也可以表示张量中轴的个数(比如 5D 张量),这有时会令人感到混乱。
对于后一种情况,技术上更准确的说法是 5 阶张量(张量的阶数即轴的个数),但 5D 张量这种模糊的写法更常见。
2.2.3 矩阵(2D 张量)
向量组成的数组叫作矩阵(matrix)或二维张量(2D 张量)。
矩阵有 2 个轴(通常叫作行和列)。你可以将矩阵直观地理解为数字组成的矩形网格。
>>> x = np.array([[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]])
>>> x.ndim
2第一个轴上的元素叫作行(row),第二个轴上的元素叫作列(column)。
在上面的例子中,[5, 78, 2, 34, 0] 是 x 的第一行,[5, 6, 7] 是第一列。
2.2.4 3D 张量与更高维张量
将多个矩阵组合成一个新的数组,可以得到一个 3D 张量,你可以将其直观地理解为数字组成的立方体。下面是一个 Numpy 的 3D 张量。
>>> x = np.array([[[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]],[[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]],[[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]]])
>>> x.ndim
3将多个 3D 张量组合成一个数组,可以创建一个 4D 张量,以此类推。深度学习处理的一般是 0D 到 4D 的张量,但处理视频数据时可能会遇到 5D 张量。
2.2.5 关键属性
张量是由以下三个关键属性来定义的。
轴的个数(阶)。例如,3D 张量有 3 个轴,矩阵有 2 个轴。这在 Numpy 等 Python 库中也叫张量的 ndim。
形状。这是一个整数元组,表示张量沿每个轴的维度大小(元素个数)。例如,前面矩阵示例的形状为 (3, 5),3D 张量示例的形状为 (3, 3, 5)。向量的形状只包含一个元素,比如 (5,),而标量的形状为空,即 ()。
数据类型(在 Python 库中通常叫作 dtype)。这是张量中所包含数据的类型,例如,张量的类型可以是 float32、uint8、float64 等。
在极少数情况下,你可能会遇到字符(char)张量。注意,Numpy(以及大多数其他库)中不存在字符串张量,因为张量存储在预先分配的连续内存段中,而字符串的长度是可变的,无法用这种方式存储。
为了具体说明,我们回头看一下 MNIST 例子中处理的数据。首先加载 MNIST 数据集。
from keras.datasets import mnist(train_images, train_labels), (test_images, test_labels) = mnist.load_data()print('train_images.ndim:',train_images.ndim)
print('train_images.shape:',train_images.shape)
print('train_images.dtype:',train_images.dtype)train_images.ndim: 3
train_images.shape: (60000, 28, 28)
train_images.dtype: uint8所以,这里 train_images 是一个由 8 位整数组成的 3D 张量。更确切地说,它是 60 000个矩阵组成的数组,每个矩阵由 28×28 个整数组成。每个这样的矩阵都是一张灰度图像,元素取值范围为 0~255。
#2-8 显示第 4 个数字
digit = train_images[4]
import matplotlib.pyplot as plt
plt.imshow(digit, cmap=plt.cm.binary)
plt.show()train_images[4]就是train数据库中的第5张图片(从0开始计数)

2.2.6 在 Numpy 中操作张量
my_slice = train_images[10:100]
print('my_slice.shape',my_slice.shape)运行结果:
my_slice.shape (90, 28, 28)my_slice = train_images[10:100, :, :]
print('my_slice.shape2:',my_slice.shape)my_slice = train_images[10:100, 0:28, 0:28]
print('my_slice.shape3:',my_slice.shape)my_slice.shape2: (90, 28, 28)
my_slice.shape3: (90, 28, 28)my_slice = train_images[:, 14:, 14:]
print('my_slice.shape4:',my_slice.shape)my_slice = train_images[:, 7:-7, 7:-7]
print('my_slice.shape5:',my_slice.shape)my_slice.shape4: (60000, 14, 14)
my_slice.shape5: (60000, 14, 14)2.2.7 数据批量的概念
2.2.8 现实世界中的数据张量
2.2.9 向量数据
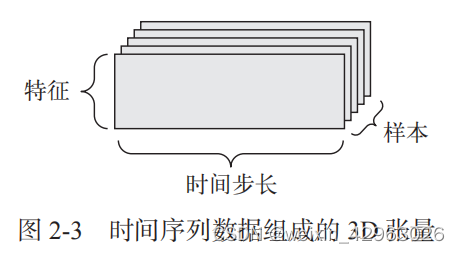
2.2.10 时间序列数据或序列数据
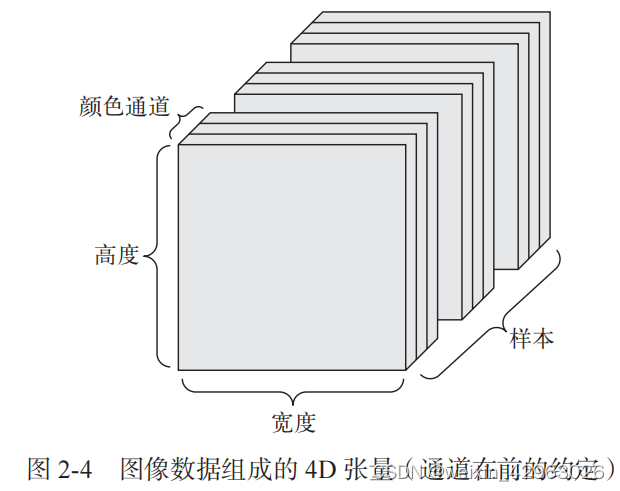
2.2.11 图像数据
2.2.12 视频数据
2.3 神经网络的“齿轮”:张量运算
与此类似,深度神经网络学到的所有变换也都可以简化为数值数据张量上的一些张量运算(tensor
2.3.1 逐元素运算
def naive_relu(x):# x 是一个 Numpy 的 2D 张量assert len(x.shape) == 2# 避免覆盖输入张量x = x.copy()# x 是一个 Numpy 的 2D 张量for i in range(x.shape[0]):for j in range(x.shape[1]):x[i, j] = max(x[i, j], 0)return xdef naive_add(x, y):assert len(x.shape) == 2assert x.shape == y.shapex = x.copy()for i in range(x.shape[0]):for j in range(x.shape[1]):x[i, j] += y[i, j]return x在实践中处理 Numpy 数组时,这些运算都是优化好的 Numpy 内置函数,这些函数将大量
import numpy as np
z = x + y
z = np.maximum(z, 0.)2.3.2 广播
def naive_add_matrix_and_vector(x, y):# x 是一个 Numpy 的 2D 张量assert len(x.shape) == 2# y 是一个 Numpy 向量assert len(y.shape) == 1assert x.shape[1] == y.shape[0]# 避免覆盖输入张量x = x.copy()for i in range(x.shape[0]):for j in range(x.shape[1]):x[i, j] += y[j]return ximport numpy as np
# x 是形状为 (64, 3, 32, 10) 的随机张量
x = np.random.random((64, 3, 32, 10))
# y 是形状为 (32, 10) 的随机张量
y = np.random.random((32, 10))
# 输出 z 的形状是 (64, 3, 32, 10),与 x 相同
z = np.maximum(x, y)2.3.3 张量点积
import numpy as np
z = np.dot(x, y)def naive_vector_dot(x, y):# x 和 y 都是 Numpy 向量assert len(x.shape) == 1assert len(y.shape) == 1assert x.shape[0] == y.shape[0]z = 0.for i in range(x.shape[0]):z += x[i] * y[i]return zdef naive_matrix_vector_dot(x, y):# x 是一个 Numpy 矩阵assert len(x.shape) == 2# y 是一个 Numpy 向量assert len(y.shape) == 1# x 的第 1 维和 y 的第 0 维大小必须相同assert x.shape[1] == y.shape[0]# 这个运算返回一个全是 0 的向量,# 其形状与 x.shape[0] 相同z = np.zeros(x.shape[0])for i in range(x.shape[0]):for j in range(x.shape[1]):z[i] += x[i, j] * y[j]return zdef naive_matrix_vector_dot(x, y):z = np.zeros(x.shape[0])for i in range(x.shape[0]):z[i] = naive_vector_dot(x[i, :], y)return z注意,如果两个张量中有一个的 ndim 大于 1,那么 dot 运算就不再是对称的,也就是说,dot(x, y) 不等于 dot(y, x)。
def naive_matrix_dot(x, y):# x 和 y 都 是Numpy矩阵,二维张量assert len(x.shape) == 2assert len(y.shape) == 2# x 的第 1 维和 y 的第 0 维大小必须相同assert x.shape[1] == y.shape[0]# 这个运算返回特定形状的零矩阵z = np.zeros((x.shape[0], y.shape[1]))# 遍历 x 的所有行……for i in range(x.shape[0]):# 然后遍历 y 的所有列for j in range(y.shape[1]):row_x = x[i, :]column_y = y[:, j]z[i, j] = naive_vector_dot(row_x, column_y)return z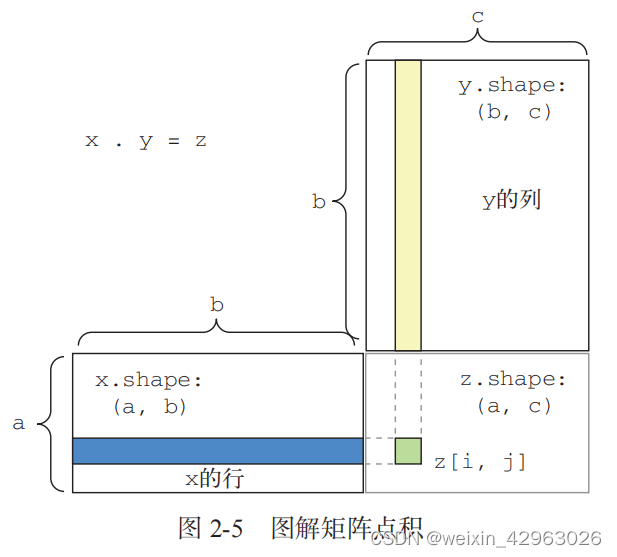
2.3.4 张量变形
train_images = train_images.reshape((60000, 28 * 28))import numpy as npx = np.array([[0., 1.],[2., 3.],[4., 5.]])
print('x=', x)
print(x.shape)x = x.reshape((6, 1))
print('x=', x)x = x.reshape((2, 3))
print('x=', x)x= [[0. 1.][2. 3.][4. 5.]]
(3, 2)
x= [[0.][1.][2.][3.][4.][5.]]
x= [[0. 1. 2.][3. 4. 5.]]x = np.zeros((3, 4))
x = np.transpose(x)
print(x.shape)(4, 3)2.3.5 张量运算的几何解释


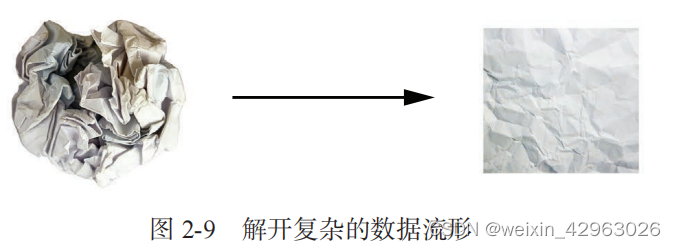
2.3.6 深度学习的几何解释
2.4 神经网络的“引擎”:基于梯度的优化
output = relu(dot(W, input) + b)最终得到的网络在训练数据上的损失非常小,即预测值 y_pred 和预期目标 y 之间的距离非常小。网络“学会”将输入映射到正确的目标。乍一看可能像魔法一样,但如果你将其简化为基本步骤,那么会变得非常简单。
2.4.1 什么是导数

2.4.2 张量运算的导数:梯度
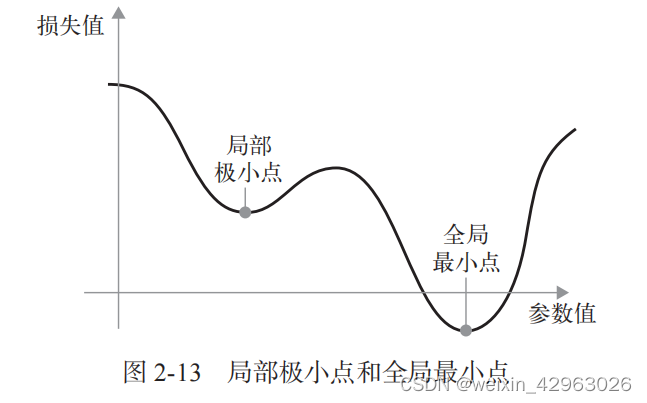
2.4.3 随机梯度下降
相反,你可以使用 2.4 节开头总结的四步算法:基于当前在随机数据批量上的损失,一点一点地对参数进行调节。由于处理的是一个可微函数,你可以计算出它的梯度,从而有效地实现第四步。沿着梯度的反方向更新权重,损失每次都会变小一点。


2.4.4 链式求导:反向传播算法
2.5 回顾第一个例子
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))network.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy'])network.fit(train_images, train_labels, epochs=5, batch_size=128)本章小结
相关文章:

第2章-神经网络的数学基础——python深度学习
第2章 神经网络的数学基础 2.1 初识神经网络 我们来看一个具体的神经网络示例,使用 Python 的 Keras 库 来学习手写数字分类。 我们这里要解决的问题是, 将手写数字的灰度图像(28 像素28 像素)划分到 10 个类别 中(0…...

【Docker】Docker学习⑧ - Docker仓库之分布式Harbor
【Docker】Docker学习⑧ - Docker仓库之分布式Harbor 一、Docker简介二、Docker安装及基础命令介绍三、Docker镜像管理四、Docker镜像与制作五、Docker数据管理六、网络部分七、Docker仓库之单机Dokcer Registry八、 Docker仓库之分布式Harbor1 Harbor功能官方介绍2 安装Harbor…...
一行命令在 wsl-ubuntu 中使用 Docker 启动 Windows
在 wsl-ubuntu 中使用 Docker 启动 Windows 0. 背景1. 验证我的系统是否支持 KVM?2. 使用 Docker 启动 Windows3. 访问 Docker 启动的 Windows4. Docker Hub 地址5. Github 地址 0. 背景 我们可以在 Windows 系统使用安装 wsl-ubuntu,今天玩玩在 wsl-ub…...
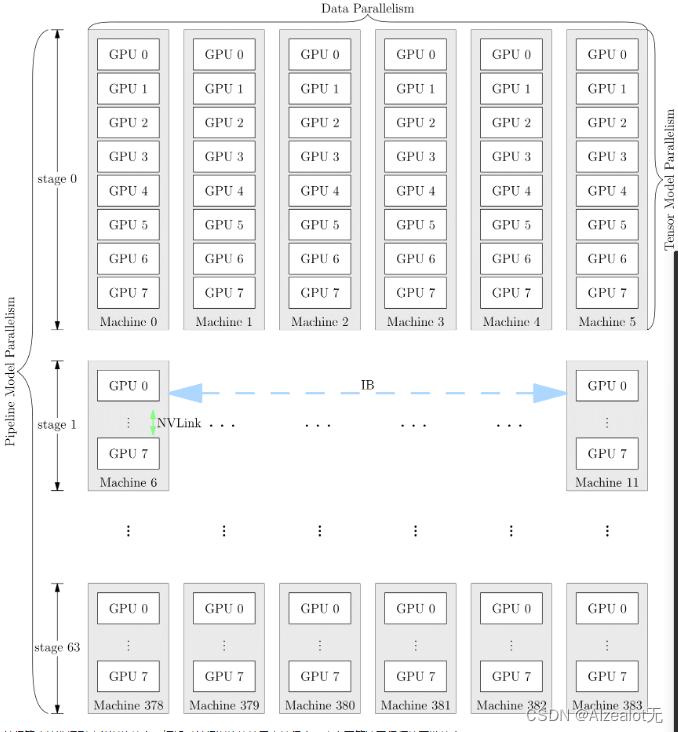
Datawhale 组队学习之大模型理论基础 Task7 分布式训练
第8章 分布式训练 8.1 为什么分布式训练越来越流行 近年来,模型规模越来越大,对硬件(算力、内存)的发展提出要求。因为内存墙的存在,单一设持续提高芯片的集成越来越困难,难以跟上模型扩大的需求。 为了…...

05-使用结构体构建相关数据
上一篇: 04-了解所有权 结构体(struct)是一种自定义数据类型,可以将多个相关值打包命名,组成一个有意义的组。如果你熟悉面向对象的语言,那么结构体就像是对象的数据属性。在本章中,我们将对元组…...

【Android】Android中的系统镜像由什么组成?
文章目录 总览Boot Loader 的加锁与解锁Boot 镜像内核RAM diskARM 中的设备树 (Device Tree) /System 和/Data 分区镜像参考 总览 各种Android设备都只能刷专门为相应型号的设备定制的镜像。 厂商会提供一套系统镜像把它作为“出厂默认”的 Android 系统刷在设备上。 一个完…...
day7【ROS关键组件】)
仿真机器人-深度学习CV和激光雷达感知(项目2)day7【ROS关键组件】
文章目录 前言Launch 文件了解 XML 文件Launch 文件作用Launch 文件常用标签实例--作业1的 Launch 文件TF Tree介绍发布坐标变换--海龟例程获取坐标变换--海龟自动跟随例程rqt_工作箱前言 💫你好,我是辰chen,本文旨在准备考研复试或就业 💫本文内容是我为复试准备的第二个…...

解锁一些SQL注入的姿势
昨天课堂上布置了要去看一些sql注入的案例,以下是我的心得: 1.新方法 打了sqli的前十关,我发现一般都是联合查询,但是有没有不是联合查询的方法呢…...
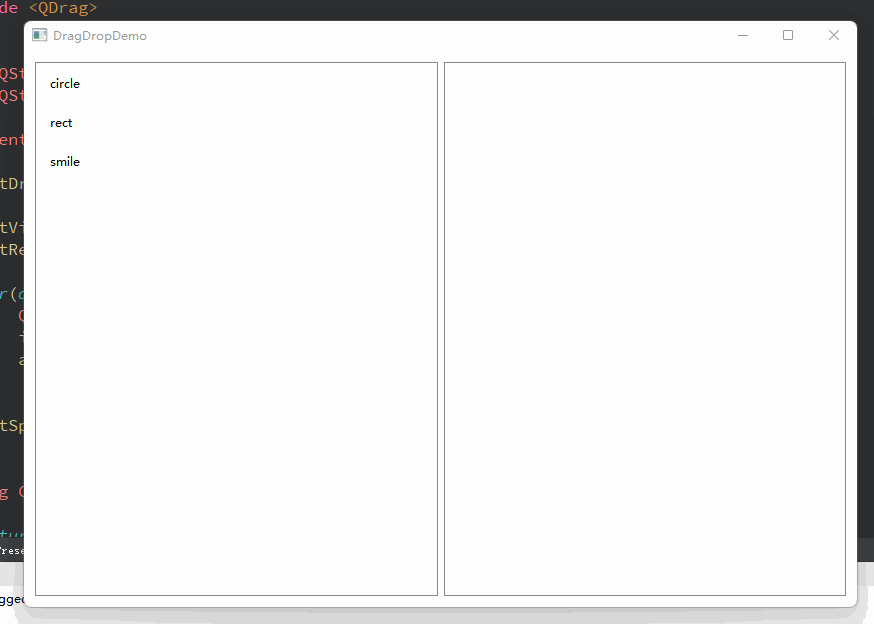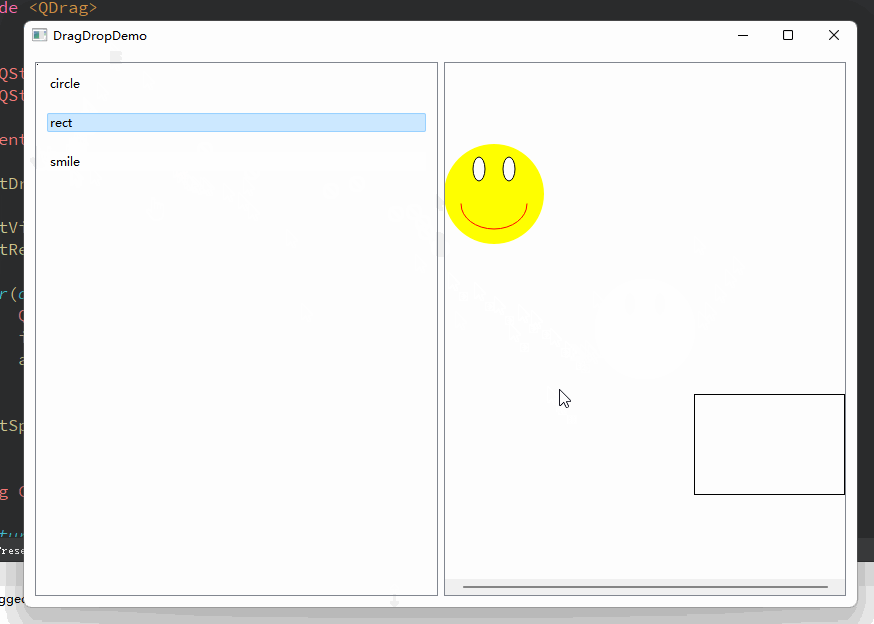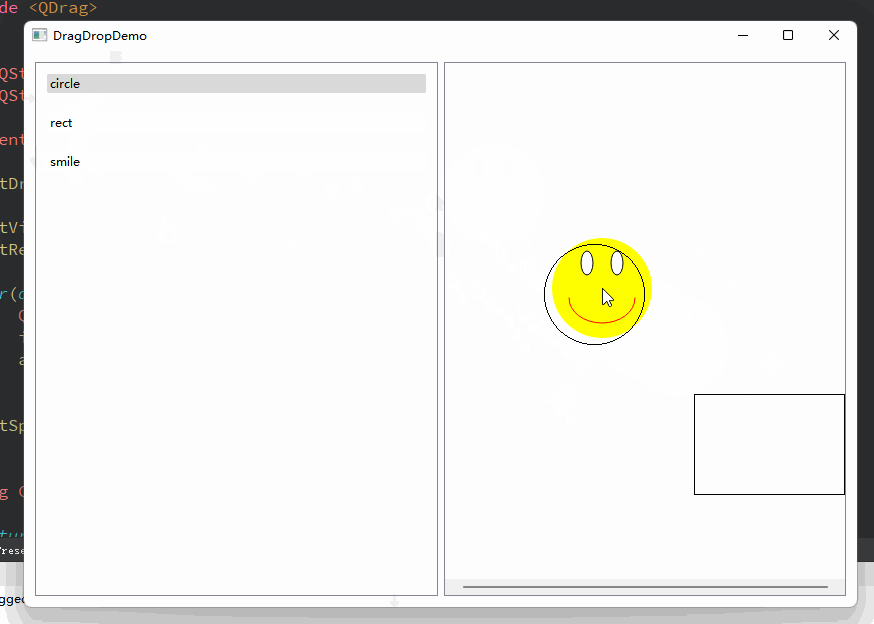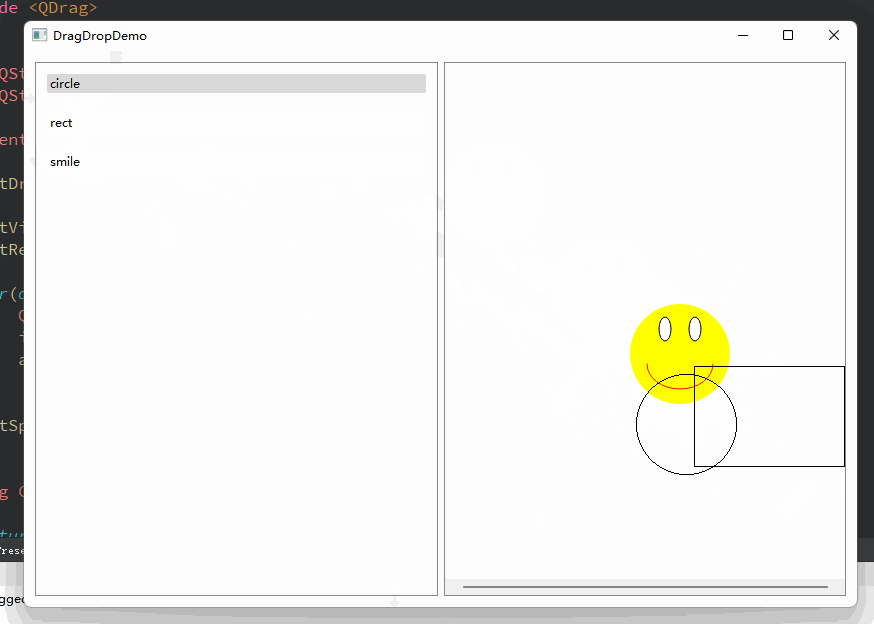
Qt 拖拽事件示例
一、引子 拖拽这个动作,在桌面应用程序中是非常实用和具有很友好的交互体验的。我们常见的譬如有,将文件拖拽到某个窗口打开,或者拖拽文件到指定位置上传;在绘图软件中,选中某个模板、并拖拽到画布上,画布上变回绘制该模板的图像… 诸如此类,数不胜数。 那么,在Qt中我…...
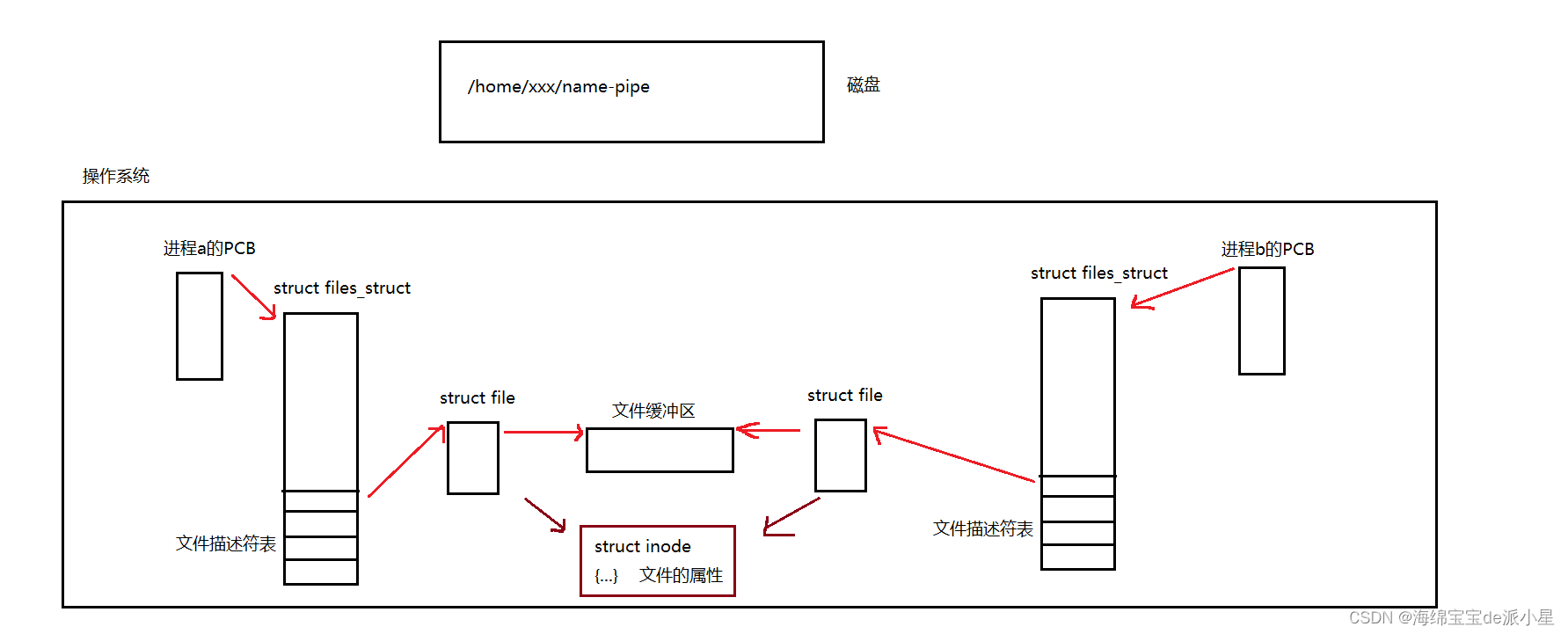
Linux:命名管道及其实现原理
文章目录 命名管道指令级命名管道代码级命名管道 本篇要引入的内容是命名管道 命名管道 前面的总结中已经搞定了匿名管道,但是匿名管道有一个很严重的问题,它只允许具有血缘关系的进程进行通信,那如果是两个不相关的进程进行通信࿰…...

实习记录——第五天
今天我的心情不是很美丽,昨天晚上没怎么睡好,因为我一直在想离不离开实验室?该怎么说的事情?但是又觉得这个项目还没有完全结束,冒昧提这个事情是不是不好?最终也没得出一个结论,晚上睡得也不踏…...
Kotlin 教程(环境搭建)
Kotlin IntelliJ IDEA环境搭建 IntelliJ IDEA 免费的社区版下载地址:Download IntelliJ IDEA – The Leading Java and Kotlin IDE 下载安装后,我们就可以使用该工具来创建项目,创建过程需要选择 SDK, Kotlin 与 JDK 1.6 一起使…...
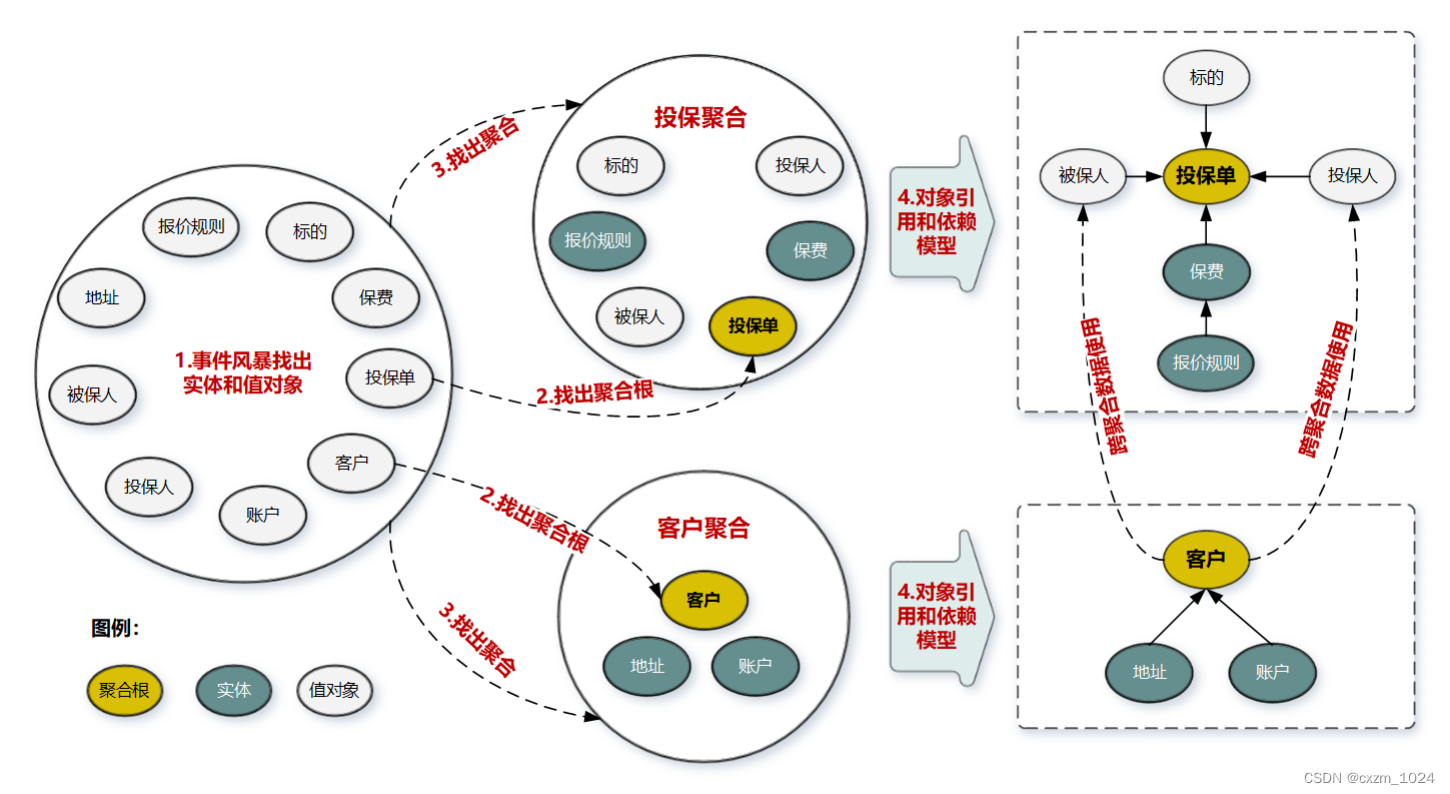
04.领域驱动设计:了解聚合和聚合根,怎样设计聚合-学习总结
目录 1、概述 2、聚合 3、聚合根 4、怎么设计聚合 4.1 聚合的构建过程主要步骤 第 1 步:采用事件风暴。 第 2 步:选出聚合根。 第 3 步:找出与聚合根关联的所有紧密依赖的实体和值对象。 第 4 步:画出对象的引用和依赖模型…...

cmake-find_package链接第三方库
文章目录 基本调用形式和模块模式使用方式 之前我们是使用了绝对路径来链接OpenCV第三方库,但是现在很多库一般会自己写一些cmake文件提供给用户,用户可以直接使用其中的内置变量即可。使用的命令就是find_package。 基本调用形式和模块模式 find_packa…...
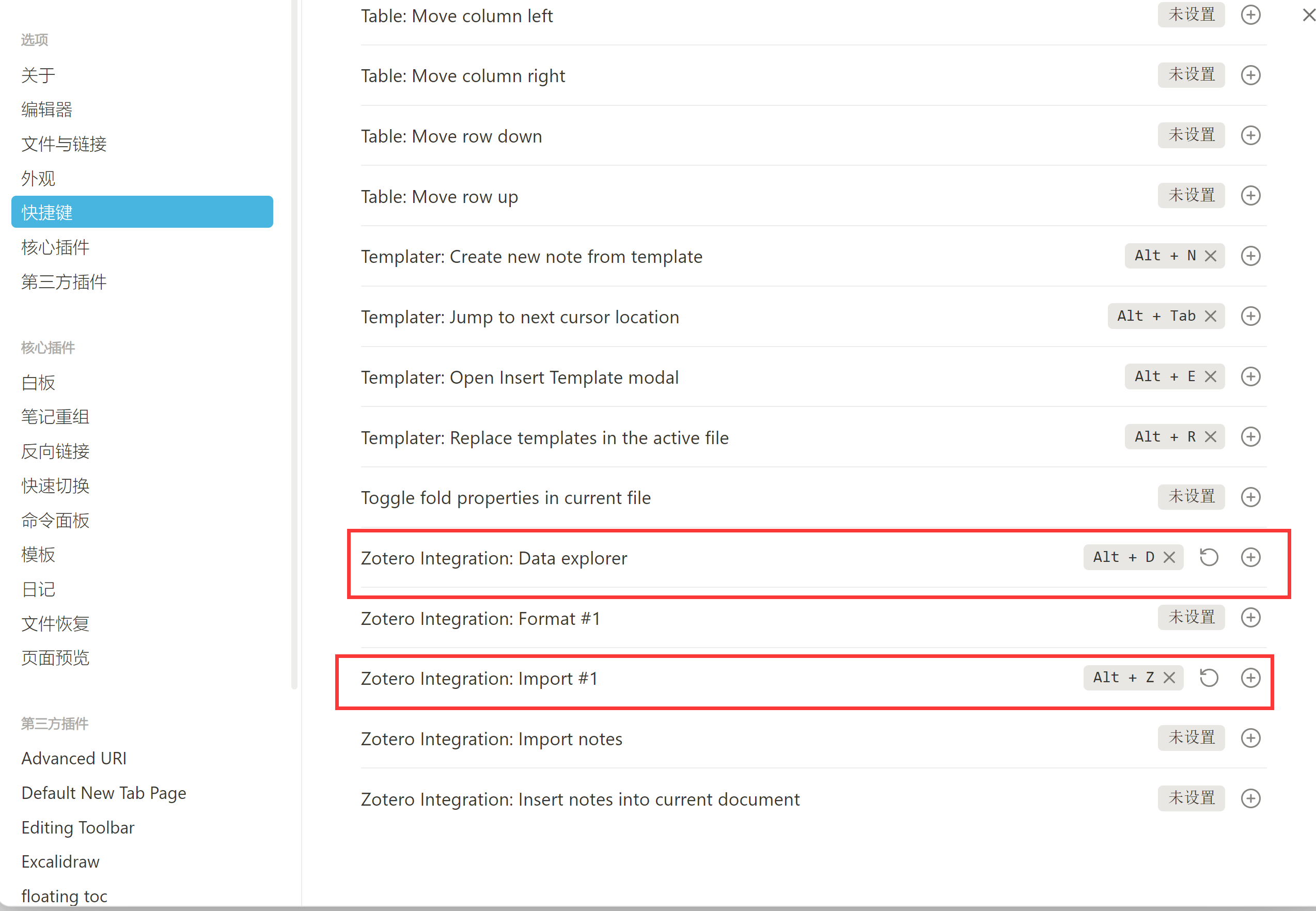
obsidian阅读pdf和文献——与zotero连用
参考: 【基于Obsidian的pdf阅读、标注,构建笔记思维导图,实现笔记标签化、碎片化,便于检索和跳转】 工作流:如何在Obsidian中阅读PDF - Eleven的文章 - 知乎 https://zhuanlan.zhihu.com/p/409627700 操作步骤 基于O…...

走方格(动态规划)
解题思路: 找边界,即行为1,列为1。 拆分问题,拆分成一次走一步,只能向右或者向下走。 解题代码: public static void main(String[] args) {int [][]arrnew int[31][31];Scanner scnew Scanner(Sys…...
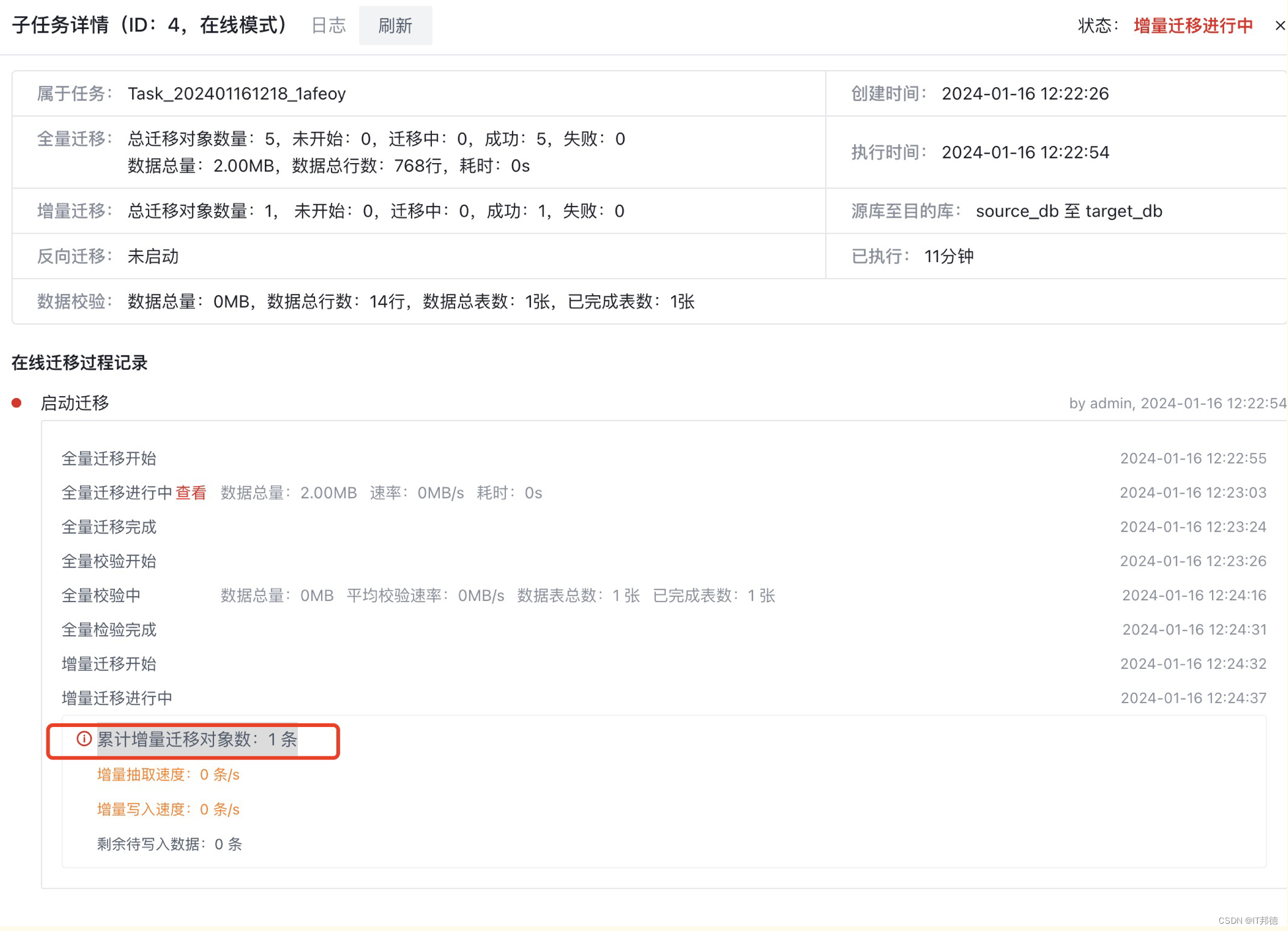
基于DataKit迁移MySQL到openGauss
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
API网关-Apinto压缩包方式自动化安装配置教程
文章目录 前言一、Apinto安装教程1. 复制脚本2. 增加执行权限3. 执行脚本4. Apinto命令4.1 启动Apinto4.2 停止Apinto4.3 重启Apinto4.4 查看Apinto版本信息4.5 加入Apinto集群4.6 离开Apinto集群4.7 查看Apinto节点信息 5. 卸载Apinto 二、Apserver(Apinto Dashboard V3)安装教…...

内网穿透natapp使用教程(Linux)
我的使用场景:在家访问学校服务器,由于不在一个局域网,所以需要使用内网穿透,我使用的是natapp。需要在有局域网的时候做好以下步骤。 (natapp官网:https://natapp.cn/) 1. 下载客户端 &#x…...

php函数 二
一 字符串包含 1.1 str_starts_with(string $haystack, string $needle) php8版本中新函数。 检查字符串是否以指定子串开头,区分大小写。返回布尔值。 $haystack待判断的字符串,$needle需要查询的内容。 function test1() {$str "Qwe asd zx…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
