当前位置： 首页 > news >正文

HMM-维特比算法

news 2025/11/5 23:10:26

HMM-维特比算法（viterbi）

  • HMM回顾
  • 隐马科夫链解法：维特比算法（Viterbi）

HMM回顾

这个不知道的可以去看看HMM
最终的公式可以解释主要分为两个部分：

  • P(xi|yi)，发射概率，字面意思是从一个词性中发射/生成出某一个单词的概率
  • P(yi|yi-1)，转移概率，表示从一个词性转移到下一个词性的概率
    这两个概率都可以通过标注文档中统计得出

隐马科夫链解法：维特比算法（Viterbi）

维特比算法其思想就是动态规划，下面以HMM进行词性标注讲解维特比算法。
在这里插入图片描述

上图中，我们需要对 “natural language processing ( nlp )” 这句话进行词性标注。最终目标是找到下图所示的最优可能路径。
在这里插入图片描述

求解顺序：

  1. 在natural这个词中（第一列），我们要保留所有可能的词性，因为每个词性后边都可能出现最优路径，这里需要求的概率是P(“natural”|词性)，这个是可以根据我们输入的训练集（文档）统计得出。
  2. 在第二列中，我们需要求解发射概率和转移概率。例如JJ，我们可以分别求出JJ->NN，JJ->JJ，JJ->VB，JJ->LRB，JJ->RRB的转移概率以及P(“language”|词性)的发射概率，发射概率*转移概率值最大的路径即为JJ的最优路径，同理我们可以对所有的词性都求出的一个最优路径。大概样子就变成了如下图所示（示意图，嘻嘻）
    在这里插入图片描述

注：我们在这里求解发射概率与转移概率的乘积时，为了避免精度损失，通常会对其取对数
3. 重复第二步，则最终结果如下图所示（示意图，嘻嘻）
*
其实最终利用维特比算法得到了“词性”（量词）条路径，从中选出概率最大路径即可

相关文章：

HMM-维特比算法

HMM-维特比算法（viterbi）HMM回顾隐马科夫链解法：维特比算法（Viterbi）HMM回顾 最终的公式可以解释主要分为两个部分： P(xi|yi)，发射概率，字面意思是从一个词性中发射/生成出某一个单…...

编程日记 2023/5/23 12:58:06

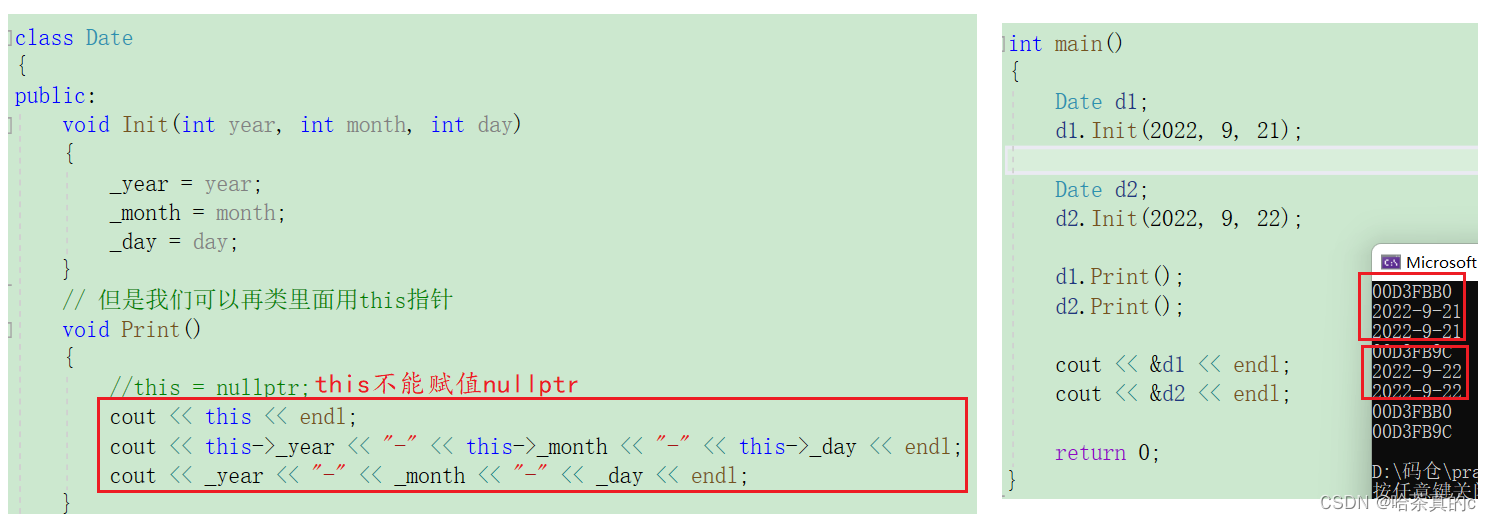
【C++初阶】2. 类和对象_1

1. 面向过程和面向对象的初步认识 2. 类的引入 C语言结构体中只能定义变量，在C中，结构体内不仅可以定义变量，也可以定义函数。比如： 之前在数据结构初阶中，用C语言方式实现的栈，结构体中只能定义变量&#…...

编程日记 2023/5/23 12:58:02

kotlin把函数作为参数转递给另一个函数

kotlin把函数作为参数转递给另一个函数 fun say(s: String, foo: (String) -> Unit) {print("hello")foo(s) }fun hi(str: String) {println(str) }fun main(args: Array<String>) {say("hello", ::hi) } 输出&#xff1a; hellohello...

编程日记 2023/5/23 12:58:00

海思嵌入式开发-005-OpenHarmony源码编译问题

海思嵌入式开发-005-OpenHarmony源码编译问题一、问题描述二、解决方案2.1解决原理2.2获取OpenHarmony 3.1.1 Release源码2.3最后解决问题&#xff0c;编译成功。一、问题描述 按照链接拉取master源码&#xff0c;出现如下问题&#xff0c;打开build.log文件 提示相应位置的文…...

编程日记 2023/5/23 12:57:57

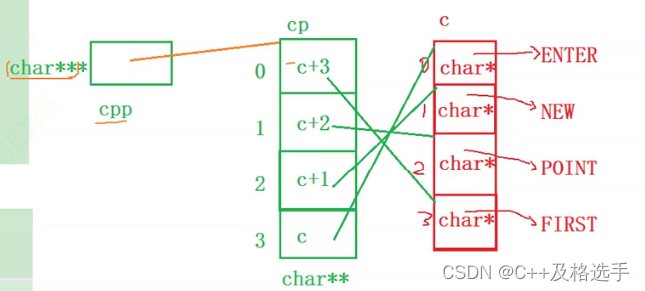
指针的进阶续（笔试题强化练习）

写在前面&#xff1a;在上次我们学习了指针的相关类型的知识&#xff0c;对指针家族的成员基本有了了解&#xff0c;这次让我们跟着一些题目来练习和补充一些知识&#xff0c;这有助于我们强化理解这些知识。 话不多说&#xff0c;我们马上开始&#xff1a; 1.指针和数组的笔…...

编程日记 2023/5/23 12:57:53

一个供参考的计算机的学习路线

本文是介绍如何成为一个Geek&#xff0c;一个真正的计算机高手。 适合有成为IT领域技术大牛的人参考。 写给大一新生和所有向深耕IT领域的人&#xff0c;避免走一些弯路。 仅代表个人想法&#xff0c;供批判性参考。 第一门入门的必备功课-语法与算法 什么是计算机&#xff1f…...

编程日记 2023/5/23 12:57:50

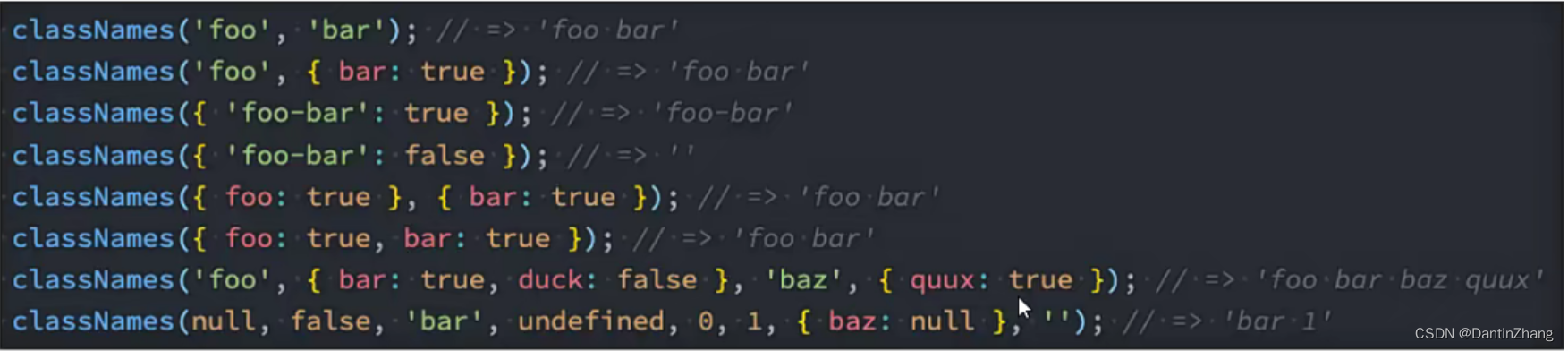
React（五）：受控组件、高阶组件、Portals、Fragment、CSS的编写方式

React&#xff08;五&#xff09;一、受控组件1.什么是受控组件&#xff08;v-model&#xff09;2.收集表单数据:input和单选框3.收集表单数据:下拉框二、非受控组件三、高阶组件1.什么是高阶组件2.高阶组件的应用13.高阶组件的应用2-注入Context4.高阶组件的应用3-登录鉴权5.高…...

编程日记 2023/5/23 12:57:48

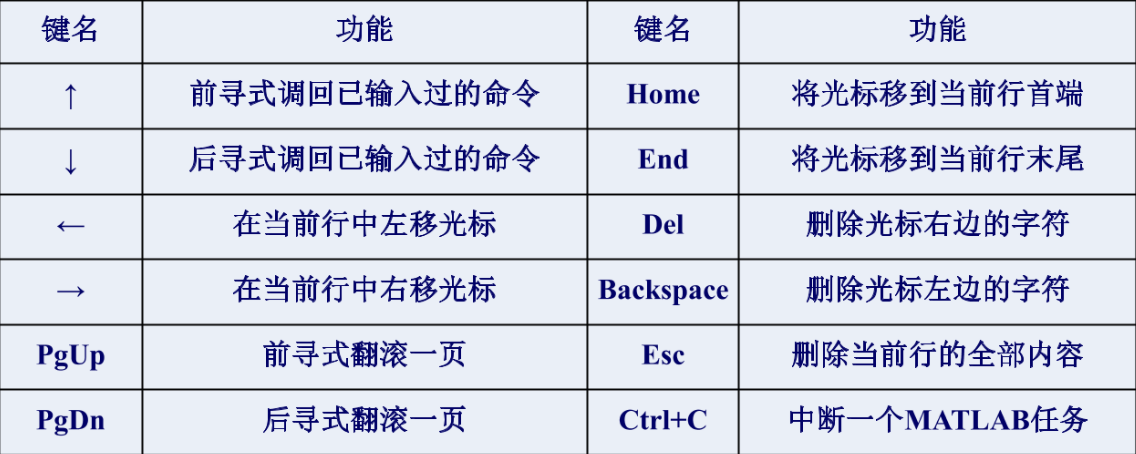
MATLAB——系统环境

MATLAB概述MATLAB的发展MATLAB:MATrix LABoratory1980年前后&#xff0c;Cleve Moler教授编写的Linpack 和Eispack的接口程序。1984年&#xff0c;MATLAB第1版(DOS版)1992年&#xff0c;MATLAB4.0版1994年&#xff0c;MATLAB 4.2版1997年&#xff0c;MATLAB 5.0版1999年&#x…...

编程日记 2023/5/23 12:57:44

2 GateWay工作流程+GateWay搭建

GateWay工作流程GateWay搭建 核心流程图如下&#xff1a; 核心概念&#xff1a; 客户端向 Spring Cloud Gateway 发出请求。如果Gateway Handler Mapping确定请求与路由匹配&#xff0c;则将其发送到Gateway Web Handler 处理程序。此处理程序通过特定于请求的Fliter链运行请求…...

编程日记 2023/5/23 12:57:39

【微信小程序】富文本rich-text的图片预览效果的几种方法

前言 使用原生小程序开发&#xff0c;实现在富文本rich-text中的图片预览效果的几种方法对比。 1.正则wx.previewImage&#xff08;有明显不足&#xff09; 一个不需要用额外组件或插件的方法&#xff1a; 思路&#xff1a;使用正则把图片的url进行剖离出来&#xff0c;push…...

编程日记 2023/5/23 12:57:37

通信网络-Socket、Java中的网络支持、多线程服务器

前言 通信网络-Socket、Java中的网络支持、多线程服务器 场景&#xff1a;使用java网络创建一个聊天室 博客地址&#xff1a;芒果橙的个人博客 文章目录前言通信网络-SocketTCP/IPTCP/IP 模型端口Java中的网络支持概念1. InetAddress2. URL3. Socket4. Datagram多线程服务器应用…...

编程日记 2023/5/23 12:57:33

搞懂 JS this、call、apply、bind

搞懂 JS this、call、apply、bind javascript 的 this ECMAScript 规范中这样写&#xff1a; this 关键字执行为当前执行环境的 ThisBinding。 MDN 上这样写&#xff1a; In most cases, the value of this is determined by how a function is called. 在绝大多数情况下&…...

编程日记 2023/5/23 12:57:30

力扣209长度最小的子数组

209. 长度最小的子数组 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl1, …, numsr-1, numsr] &#xff0c;并返回其长度。如果不存在符合条件的子数组&#xff0c;返回 0 。 示例 1&#xf…...

编程日记 2023/5/23 12:57:26

【mysql是怎样运行的】-InnoDB数据页结构

文章目录1. 数据库的存储结构&#xff1a;页1.1 磁盘与内存交互基本单位&#xff1a;页1.2 页结构概述1.3 页的上层结构2. 页的内部结构2.1 第1部分&#xff1a;文件头部和文件尾部2.1.1 File Header&#xff08;文件头部&#xff09;&#xff08;38字节&#xff09;2.1.2 File…...

编程日记 2023/5/23 12:57:24

VIM实用指南（10）语法自动补全插件coc.nvim

最近发现了一个新的自动补全插件coc.nvim异步&#xff0c;nodejs后端&#xff0c;配合它自身的lsp支持用起来非常舒服&#xff0c;同样也支持lsp和snippets&#xff0c;强烈推荐&#xff0c;值得一试。 1、使用vimplug安装插件 1.进入coc.nvim 在github的主页https://github.…...

编程日记 2023/5/23 12:57:21

【Vue3 第二十二章】过渡动画

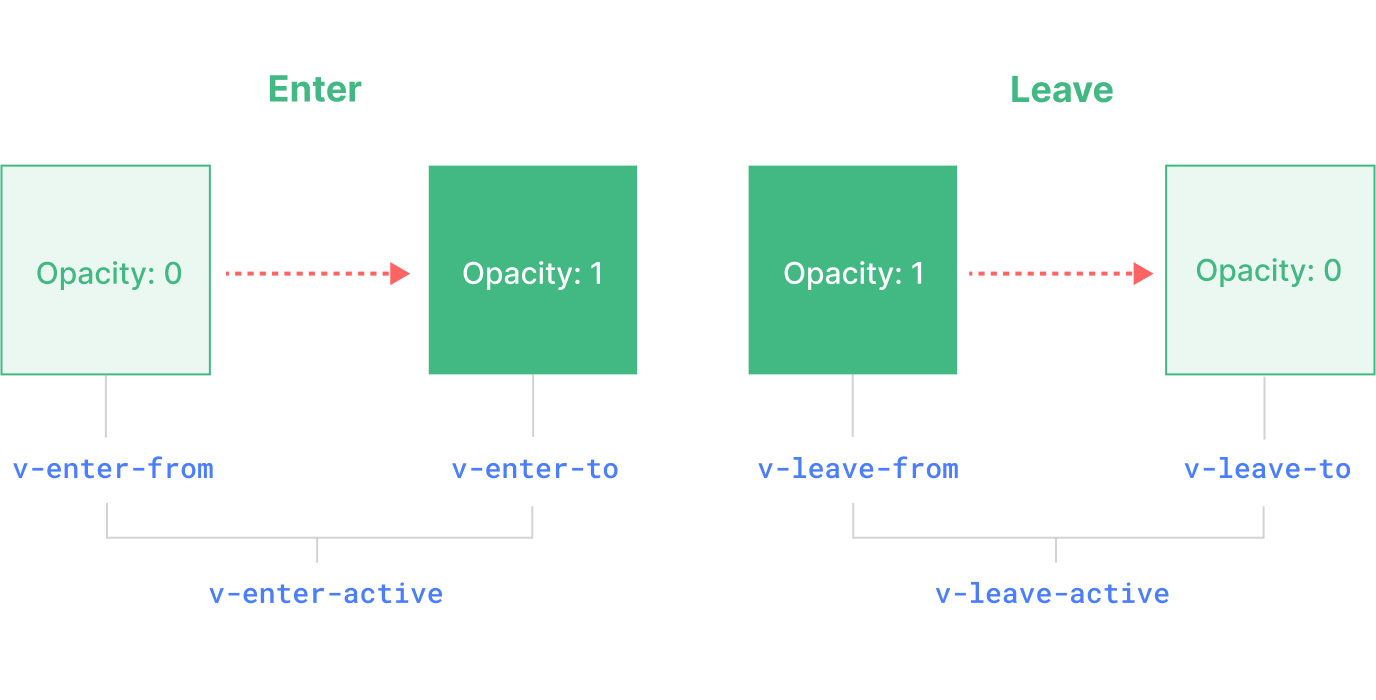
一、基本用法 <Transition> 是一个内置组件&#xff0c;这意味着它在任意别的组件中都可以被使用&#xff0c;无需注册。它可以将进入和离开动画应用到通过默认插槽传递给它的元素或组件上。进入或离开可以由以下的条件之一触发&#xff1a; 由 v-if 所触发的切换由 v-…...

编程日记 2023/5/23 12:57:19

【linux】:进程状态（僵尸进程等）以及环境变量

文章目录 前言一.进程状态 进程的优先级二.环境变量总结前言 本篇文章是接着上一篇【linux】:进程概念的后续&#xff0c;对于有基础的同学可以直接看这篇文章&#xff0c;对于初学者来说强烈建议大家从上一篇的概念开始看起&#xff0c;上一篇主要解释了冯诺依曼体系以及操…...

编程日记 2023/5/23 12:57:17

【C语言——练习题】指针，你真的学会了吗？

✨✨✨✨如果文章对你有帮助记得点赞收藏关注哦&#xff01;&#xff01;✨✨✨✨ 文章目录✨✨✨✨如果文章对你有帮助记得点赞收藏关注哦&#xff01;&#xff01;✨✨✨✨一维数组练习题&#xff1a;字符数组练习题&#xff1a;字符指针练习题&#xff1a;二维数组练习题&am…...

编程日记 2023/5/23 12:57:13

Linux用户空间与内核空间通信(Netlink通信机制)

一&#xff0c;什么是Netlink通信机制 Netlink是linux提供的用于内核和用户态进程之间的通信方式。但是注意虽然Netlink主要用于用户空间和内核空间的通信&#xff0c;但是也能用于用户空间的两个进程通信。只是进程间通信有其他很多方式&#xff0c;一般不用Netlink。除非需要…...

编程日记 2023/5/23 12:57:11

3.3日报

今天写技术文档 跟需求对其 找负责人要上游数据接口&#xff0c;并处理更新时间问题 遇到的问题&#xff1a; 1.调用上游接口&#xff0c;需要token&#xff0c;而我的数据看板是不需要登录的&#xff0c;需要其他途径获取token 不同数据使用的接口不在一个项目中&#xff…...

编程日记 2023/5/23 12:57:08

synchronized 学习

学习源&#xff1a; https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖&#xff0c;也要考虑性能问题&#xff08;场景&#xff09; 2.常见面试问题&#xff1a; sync出…...

编程新知 2025/10/23 14:31:06

应用升级/灾备测试时使用guarantee 闪回点迅速回退

1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间&#xff0c; 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点&#xff0c;不需要开启数据库闪回。…...

编程新知 2025/7/30 7:20:17

【Java学习笔记】Arrays类

Arrays 类 1. 导入包&#xff1a;import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序&#xff08;自然排序和定制排序&#xff09;Arrays.binarySearch()通过二分搜索法进行查找&#xff08;前提&#xff1a;数组是…...

编程新知 2025/10/25 11:57:30

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密

在实际项目中，用户注册、登录、修改密码等操作，都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输，在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

编程新知 2025/10/30 6:37:10

Python爬虫实战：研究feedparser库相关技术

1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代，互联网上存在着海量的信息资源。RSS（Really Simple Syndication）作为一种标准化的信息聚合技术，被广泛用于网站内容的发布和订阅。通过 RSS，用户可以方便地获取网站更新的内容，而无需频繁访问各个网站。 然而，互联网…...

编程新知 2025/8/18 9:54:31

Linux相关概念和易错知识点（42）（TCP的连接管理、可靠性、面临复杂网络的处理）

目录 1.TCP的连接管理机制&#xff08;1&#xff09;三次握手①握手过程②对握手过程的理解 &#xff08;2&#xff09;四次挥手&#xff08;3&#xff09;握手和挥手的触发&#xff08;4&#xff09;状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

编程新知 2025/11/4 11:03:40

React Native在HarmonyOS 5.0阅读类应用开发中的实践

一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强&#xff0c;React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 &#xff08;1&#xff09;使用React Native…...

编程新知 2025/8/19 2:57:37

P3 QT项目----记事本（3.8）

3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2025/10/27 2:41:32

Cloudflare 从 Nginx 到 Pingora：性能、效率与安全的全面升级

在互联网的快速发展中&#xff0c;高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司&#xff0c;近期做出了一个重大技术决策&#xff1a;弃用长期使用的 Nginx&#xff0c;转而采用其内部开发…...

编程新知 2025/10/26 5:13:27

虚拟电厂发展三大趋势：市场化、技术主导、车网互联

市场化&#xff1a;从政策驱动到多元盈利 政策全面赋能 2025年4月&#xff0c;国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》&#xff0c;首次明确虚拟电厂为“独立市场主体”&#xff0c;提出硬性目标&#xff1a;2027年全国调节能力≥2000万千瓦&#xff0…...

编程新知 2025/8/3 1:06:36