【AI面试】NMS 与 Soft NMS 的辨析
往期文章:
- AI/CV面试,直达目录汇总
- 【AI面试】L1 loss、L2 loss和Smooth L1 Loss,L1正则化和L2正则化
一、NMS
非极大值抑制(Non-Maximum Suppression,NMS),并不是深度学习时期,目标检测的产物。在传统的图像处理领域,就已经引入了NMS算法。所以,他是老算法的新使用。
- 目的: 为了消除多余的框,找到最佳的物体检测的位置
- 思想:选取那些邻域里分数最高的窗口,同时抑制那些分数低的窗口
- 本质:搜索局部极大值,抑制非极大值元素
NMS算法的步骤:
- 按某个数值从高到低进行排序(高低的可以是置信度)
- 低的依次与最高的进行
IOU的对比,超过指定阈值的,将会被踢除(分数又低,还跟高的长的相近,活该被删除),否则,就先暂时留着 - 留下来的,重复步骤1和2,直到不再发生改变为止
在Canny边缘检测、霍夫变换圆形检测里面,也都会用到NMS对多余的点、圆心进行去除。那此事排序用到的值就不再是置信度了,是梯度的值、圆心点的投票数了。
这两个更多细节的,可以参考这里:
- 图像处理笔记3-Canny边缘检测算法与原理
- 图像处理笔记4-霍夫变换直线检测、圆检测
问一个面试官常快问快答的问题:
是阈值低,最后留下的多,还是阈值高,最后留下的多?
答案是:阈值高,留下的多。
因为你的目的是要把次的、不重要的给剔除掉。那么你设定的重复阈值高,自然重复的就少,删除的也就少,最后留下来的自然就变多了。
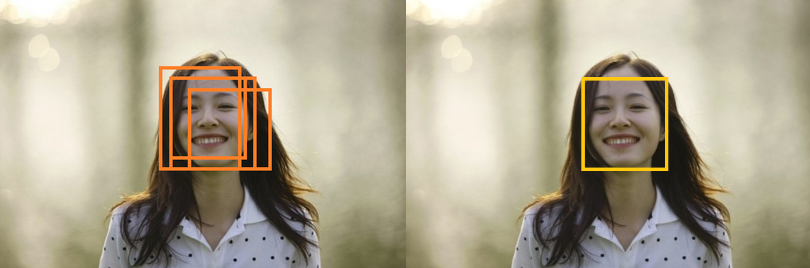
二、Soft NMS
Soft NMS 是 NMS 的一种变种,改进版本。从名字我们就大概能猜出来一些:没有NMS那么的硬(hard),比较的软(soft)。
绝大部分目标检测方法,最后都要用到 NMS-非极大值抑制进行后处理。 通常的做法是将检测框按得分排序,然后保留得分最高的框,同时删除与该框重叠面积大于一定比例的其它框。那为什么还要改进,推出一个Soft NMS 呢?
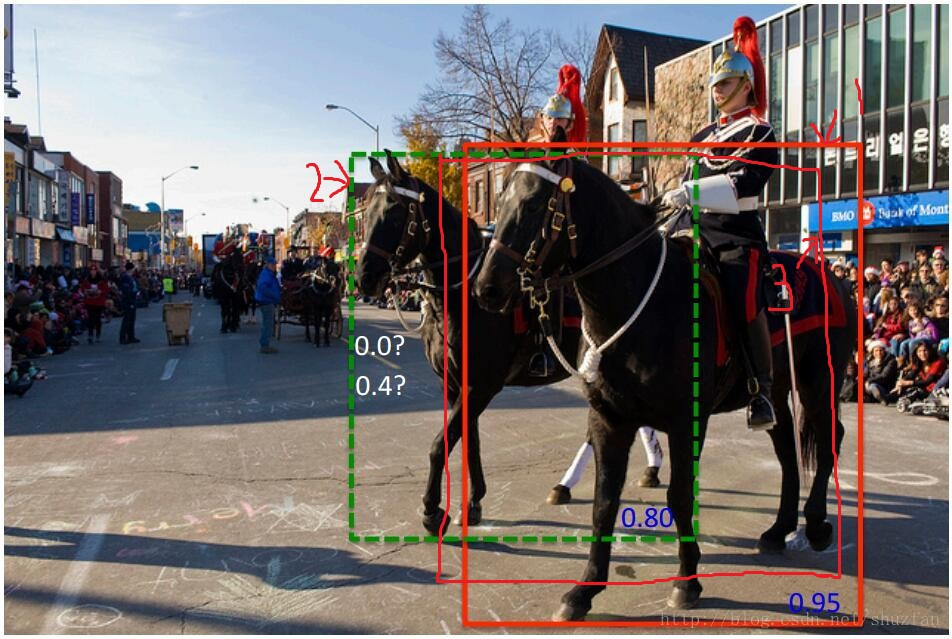
NMS 的这种贪心式方法存在如下图所示的问题:
红色框和绿色框是当前的检测结果,二者的得分分别是
0.95和0.80。如果按照传统的NMS进行处理,首先选中得分最高的红色框,然后绿色框就会因为与之重叠面积过大而被删掉。
另一方面,NMS的阈值也不太容易确定,设小了会出现绿色框因为和红色框重叠面积较大而被删掉,设置过高又容易增大误检。
 我两个都要,那该给个什么思路呢?不要粗鲁地删除所有IOU大于阈值的框,而是降低其置信度。
我两个都要,那该给个什么思路呢?不要粗鲁地删除所有IOU大于阈值的框,而是降低其置信度。
Soft NMS思路和做法如下:
- 相邻区域内(IOU超过阈值)的检测框的分数进行调整,而非彻底的抑制,从而提高了高检索率的情况下的准确率;
- 在低检索率时,仍能对物体检测性能有明显提升。
三、NMS和SoftNMS的对比学习
原来的NMS可以描述为:将IOU大于阈值的窗口的得分全部置为0。公式如下:

用人话解释下NMS的公式,就是:
- 分数低的框与分数高的框的
iou小于阈值的,不变 - 分数低的框与分数高的框的
iou大于或等于于阈值的,置信度直接置为0,也就是被踢出了
而SoftNMS可以描述为:将IOU大于阈值的窗口的得分进行改写,iou越大,(1-iou)就越小。线性加权的公式如下:

对比NMS,用人话解释下softNMS的公式,就是:
- 分数低的框与分数高的框的
iou小于阈值的,不变,与NMS处理一样 - 分数低的框与分数高的框的
iou大于或等于于阈值的,置信度不再置为0,而是通过置信分数*(1-iou),得到新的分数,进行替换.
对比总结:
- 在NMS的算法里面,对于IOU超于阈值的检测框,直接剔除;
- 而Soft NMS,对于IOU超过阈值的检测框,不是直接删除,而是改变该检测框的置信度,踢出的工作留给了置信度阈值来做。
 又回到前面两匹马的问题上来。假设
又回到前面两匹马的问题上来。假设框1的置信度是0.95,框2的置信度是0.8,还有一个框3的置信度是0.7。我们最终的目的是将框1和框2保留下来,将框3进行剔除掉。
- 假设使用的是NMS,那么框2和3都会被剔除掉,因为他们与框1的iou都比较高,很大可能性是高于阈值的,都被提除掉了。
- 那假设使用的是softNMS,框2和3的置信度就会被重新改写。2和1的iou较小,改写之后的置信度是0.4;3和1的iou较大,置信度会更低,大概是0.2。那假设筛选阈值正好是0.3,就恰好把2留下,把3踢出了。
- 但是,这里也有一个问题就是置信度的阈值如何选择?作者在这里依然使用手工设置的值,依然存在很大的局限性,所以该算法依然存在改进的空间。
针对这个问题,我也帮你们提前问了chatGPT,也给出了一个较为总结性的回答,如下所示。你们觉得它回答的如何呢?




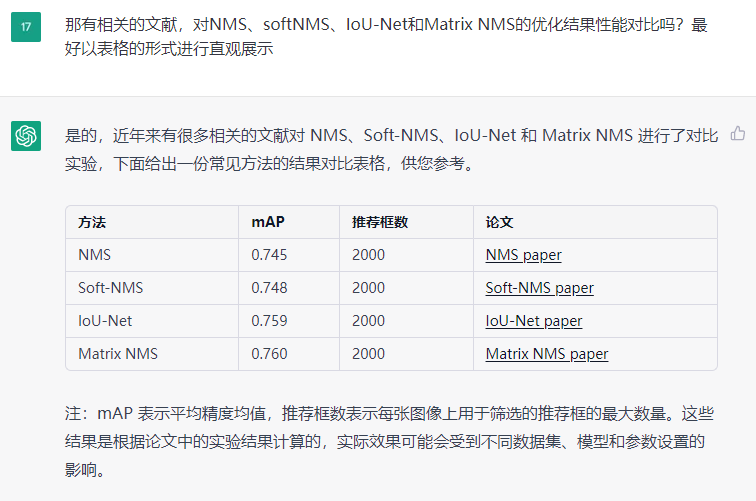
- Soft-NMS – Improving Object Detection With One Line of Code
- IOU-Net , Acquisition of Localization Confidence for Accurate Object Detection
- Matrix NMS,SOLOv2: Dynamic and Fast Instance Segmentation
通过对chatGPT的询问,我们又知道了两个NMS,分别是IoU NMS 和 Matrix NMS,这是我们新的收获。后面我们会继续补充这块内容
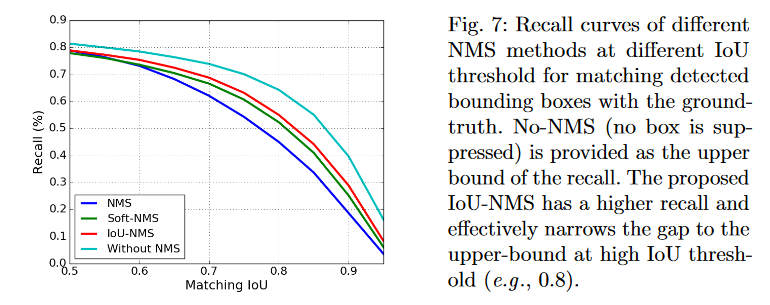
上图是IoU-Net论文的测试结果,展示了 IoU和召回率的关系,No-NMS是召回率的上界,可以看到IoU-NMS的召回率更高,且在更高的IoU下,IoU-NMS与上界的差距越小。
参考链接:
- NMS和soft-nms算法
- 哔哩哔哩视频
相关文章:

【AI面试】NMS 与 Soft NMS 的辨析
往期文章: AI/CV面试,直达目录汇总【AI面试】L1 loss、L2 loss和Smooth L1 Loss,L1正则化和L2正则化 一、NMS 非极大值抑制(Non-Maximum Suppression,NMS),并不是深度学习时期,目标…...
一文让你彻底理解Linux内核多线程(互斥锁、条件变量、读写锁、自旋锁、信号量)
一、互斥锁(同步) 在多任务操作系统中,同时运行的多个任务可能都需要使用同一种资源。这个过程有点类似于,公司部门里,我在使用着打印机打印东西的同时(还没有打印完),别人刚好也在…...
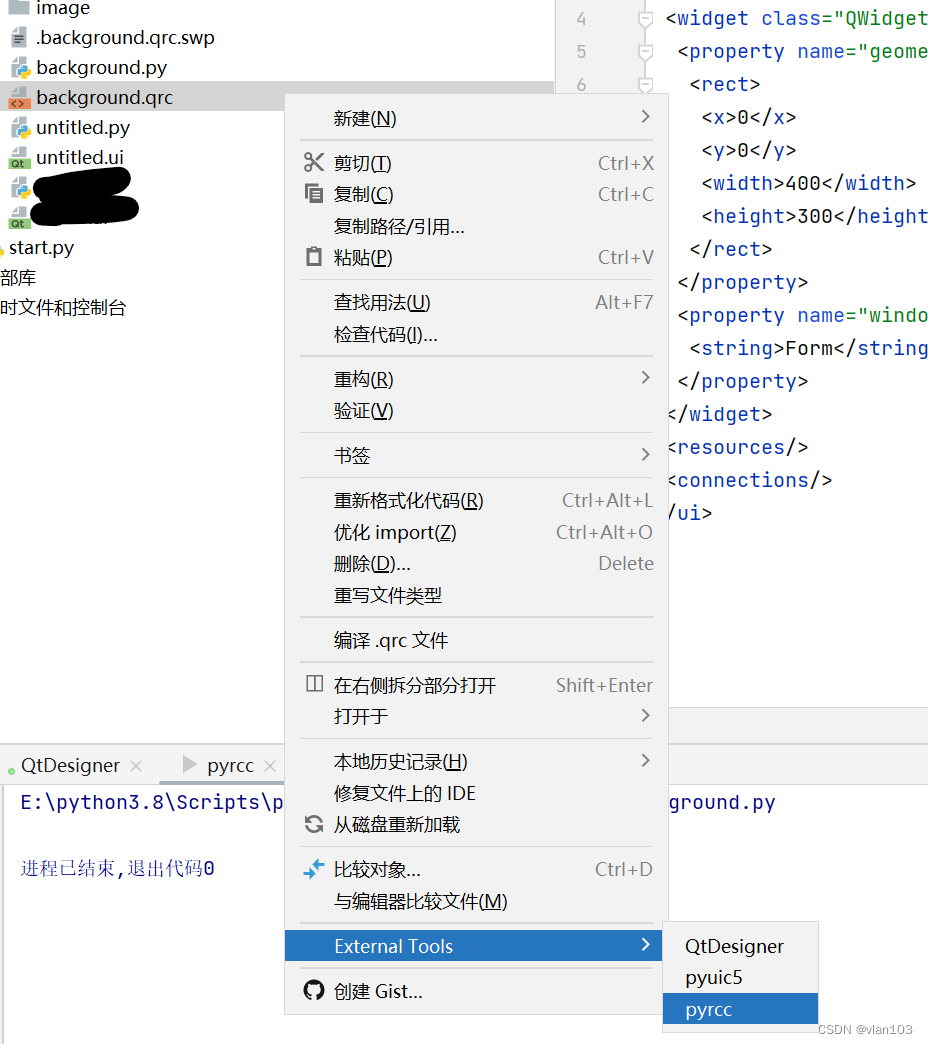
利用python写一个gui小公举--环境搭建
文章目录背景搭建环境安装必要库添加工具快捷方式检验背景 在实习过程中遇到一个问题,某项目是通过python代码实现的,而且需要一直修改参数实现功能,过程有些繁琐。虽然师兄用PHP study搭了一个网站用于查看结果,但是还是过于繁琐…...

英飞凌Tricore实战系列02_ENDINIT属性看门狗原理及应用
目录 1.概述2.ENDINIT功能及使用2.1 ENDINIT属性2.2 改写受ENDINIT保护寄存器的步骤3. Tricore 看门狗介绍及使用3.1 看门狗系统介绍3.1.1 安全看门狗介绍3.1.2 CPU看门狗介绍3.2 看门狗模式介绍3.2.1 Time-out模式3.2.2 正常模式(Normal Mode)3.2.3 禁用模式(Disabled Mode…...

Java Number类
Java Number 类是一个抽象类,它是所有数字类的基类。Java 中的数字类包括 Byte、Short、Integer、Long、Float 和 Double,它们都继承自 Number 类。Java Number 类提供了一些常用的方法,可以用于将数字类型转换为不同的格式,以及进…...
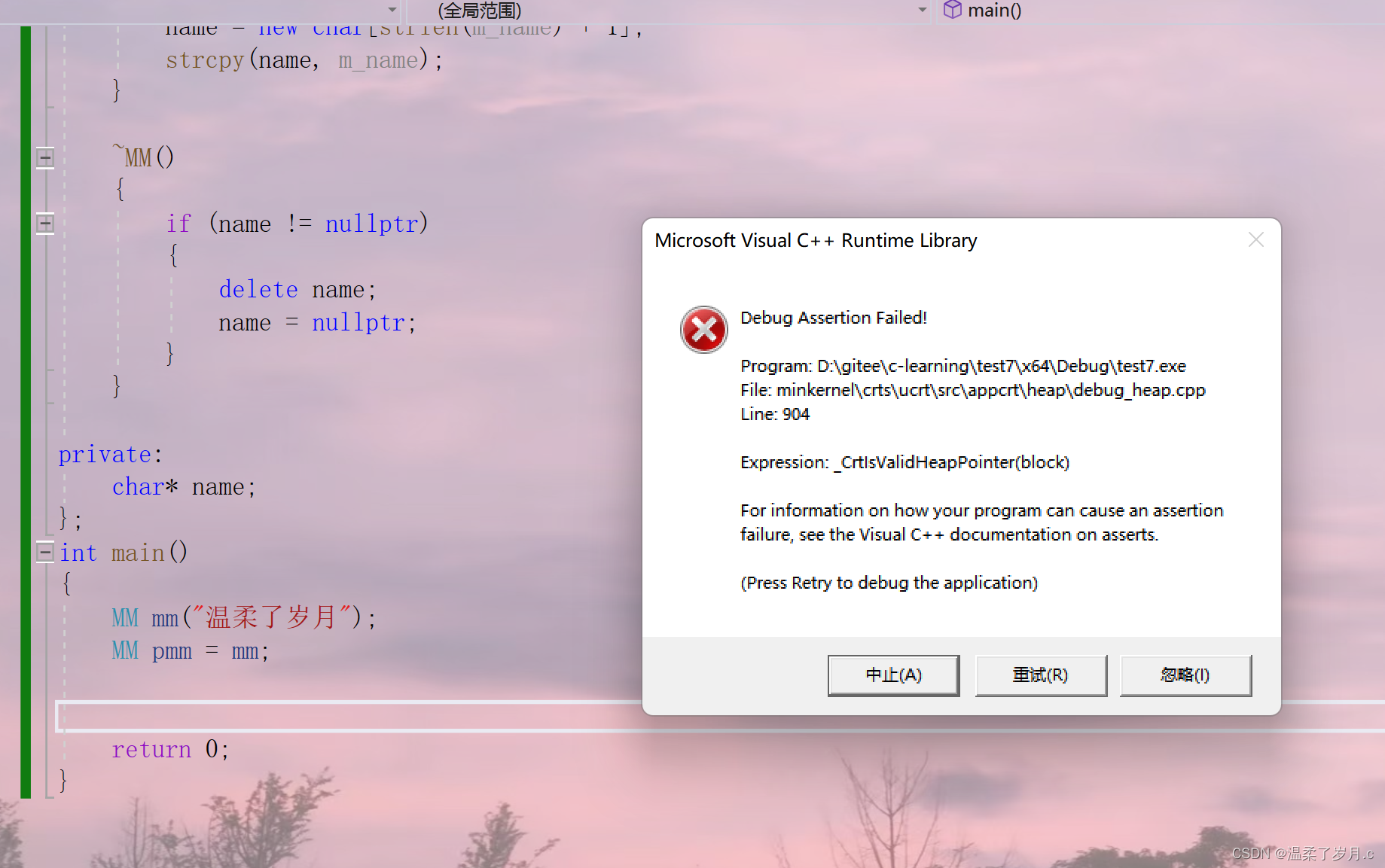
C++构造和析构
欢迎来观看温柔了岁月.c的博客 目前 设有C学习专栏 C语言项目专栏 数据结构与算法专栏 目前主要更新C学习专栏,C语言项目专栏不定时更新 待C专栏完毕,会陆续更新C项目专栏和数据结构与算法专栏 一周主要三更,星期三,星期五&#x…...
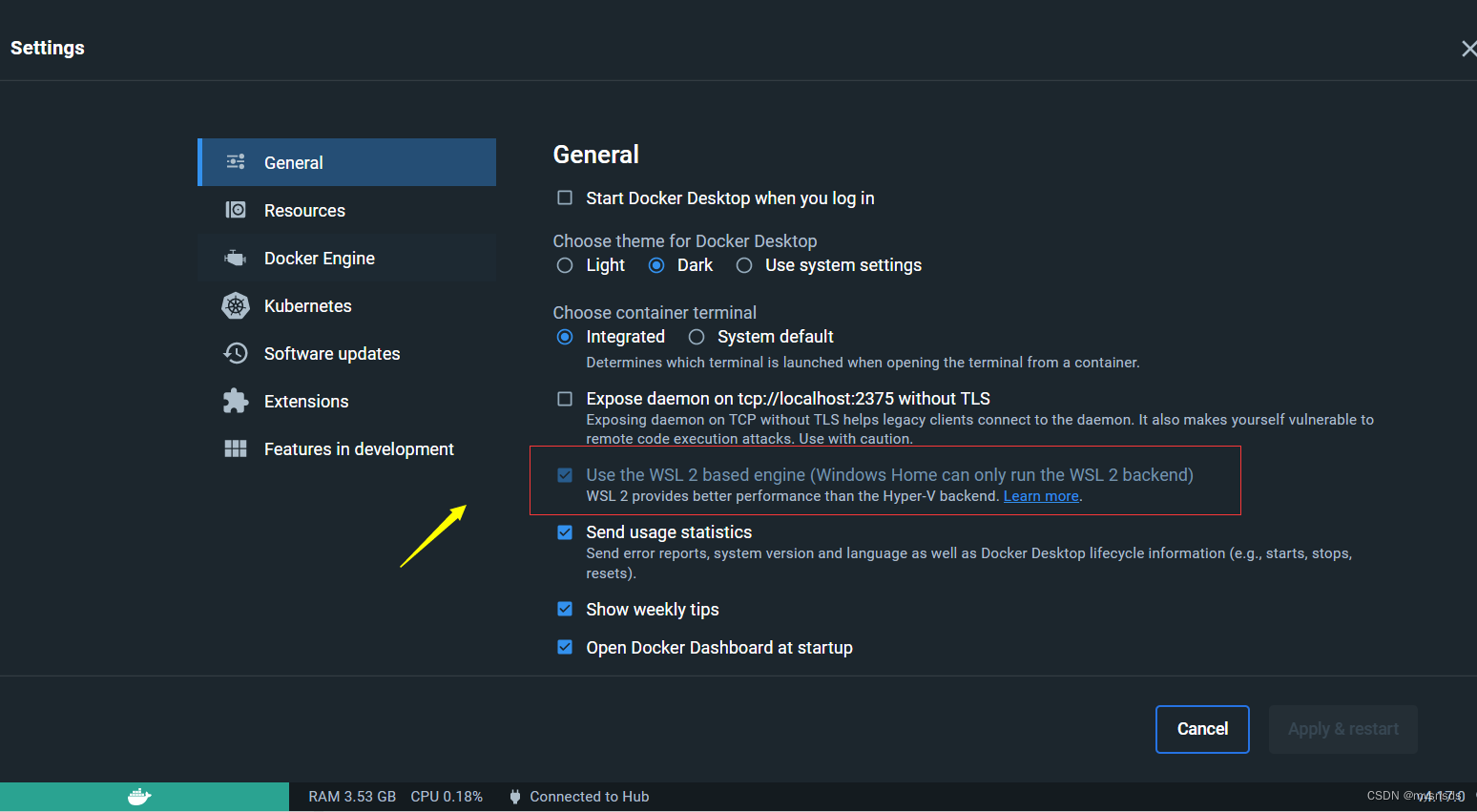
docker安装即docker连接mysql(window)
一 安装docker 1.什么是docker Docker容器与虚拟机类似,但二者在原理上不同。容器是将操作系统层虚拟化,虚拟机则是虚拟化硬件,因此容器更具有便携性、高效地利用服务器。 2.WSL2 WSL,即Windows Subsystem on Linux,中…...

HMM-维特比算法
HMM-维特比算法(viterbi)HMM回顾隐马科夫链解法:维特比算法(Viterbi)HMM回顾 最终的公式可以解释主要分为两个部分: P(xi|yi),发射概率,字面意思是从一个词性中发射/生成出某一个单…...
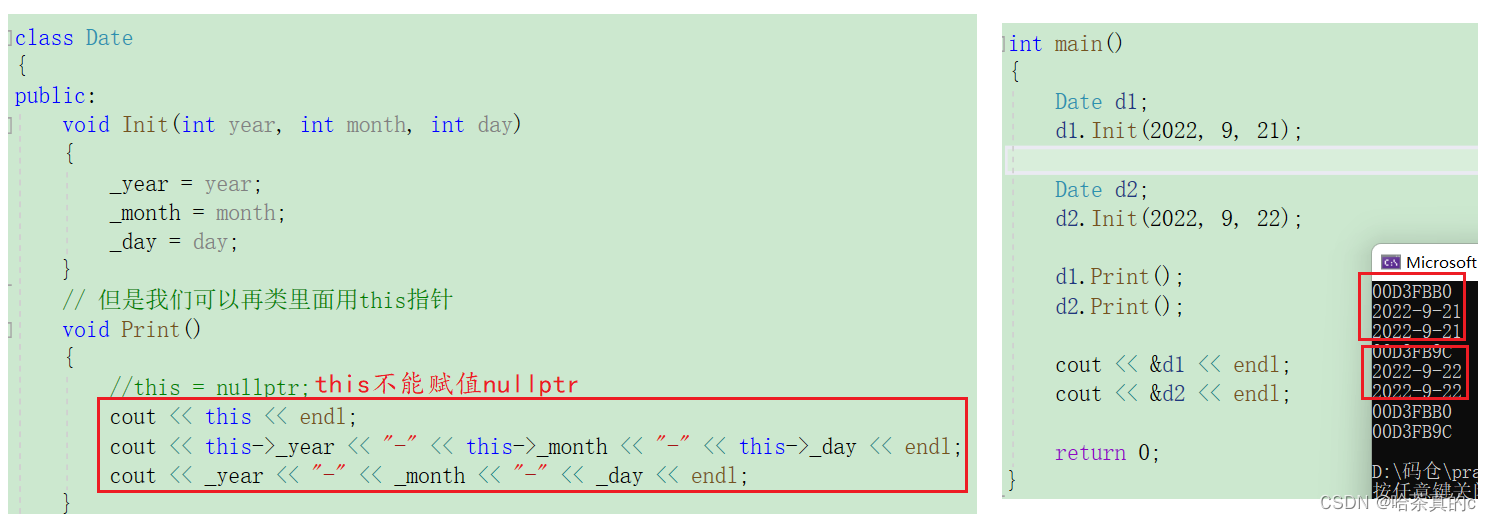
【C++初阶】2. 类和对象_1
1. 面向过程和面向对象的初步认识 2. 类的引入 C语言结构体中只能定义变量,在C中,结构体内不仅可以定义变量,也可以定义函数。比如: 之前在数据结构初阶中,用C语言方式实现的栈,结构体中只能定义变量&#…...

kotlin把函数作为参数转递给另一个函数
kotlin把函数作为参数转递给另一个函数 fun say(s: String, foo: (String) -> Unit) {print("hello")foo(s) }fun hi(str: String) {println(str) }fun main(args: Array<String>) {say("hello", ::hi) } 输出: hellohello...
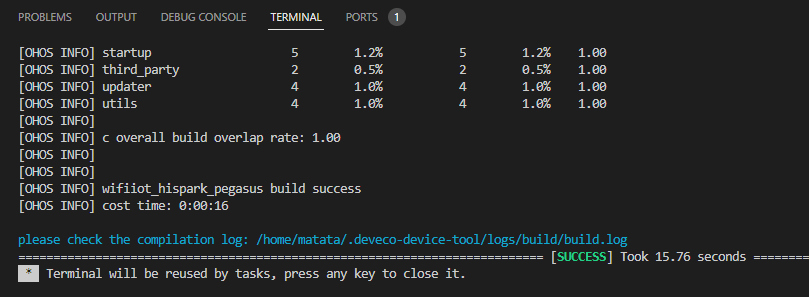
海思嵌入式开发-005-OpenHarmony源码编译问题
海思嵌入式开发-005-OpenHarmony源码编译问题一、问题描述二、解决方案2.1解决原理2.2获取OpenHarmony 3.1.1 Release源码2.3最后解决问题,编译成功。一、问题描述 按照链接拉取master源码,出现如下问题,打开build.log文件 提示相应位置的文…...
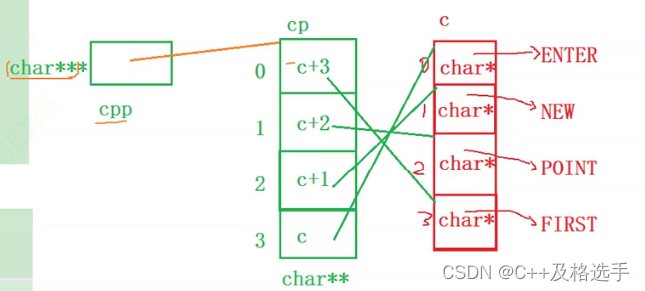
指针的进阶续(笔试题强化练习)
写在前面:在上次我们学习了指针的相关类型的知识,对指针家族的成员基本有了了解,这次让我们跟着一些题目来练习和补充一些知识,这有助于我们强化理解这些知识。 话不多说,我们马上开始: 1.指针和数组的笔…...

一个供参考的计算机的学习路线
本文是介绍如何成为一个Geek,一个真正的计算机高手。 适合有成为IT领域技术大牛的人参考。 写给大一新生和所有向深耕IT领域的人,避免走一些弯路。 仅代表个人想法,供批判性参考。 第一门入门的必备功课-语法与算法 什么是计算机?…...
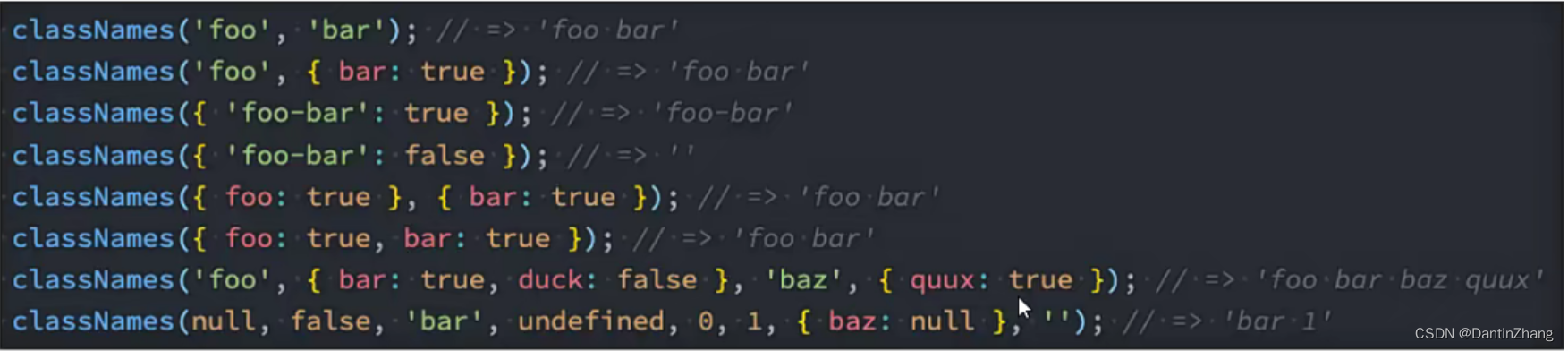
React(五):受控组件、高阶组件、Portals、Fragment、CSS的编写方式
React(五)一、受控组件1.什么是受控组件(v-model)2.收集表单数据:input和单选框3.收集表单数据:下拉框二、非受控组件三、高阶组件1.什么是高阶组件2.高阶组件的应用13.高阶组件的应用2-注入Context4.高阶组件的应用3-登录鉴权5.高…...
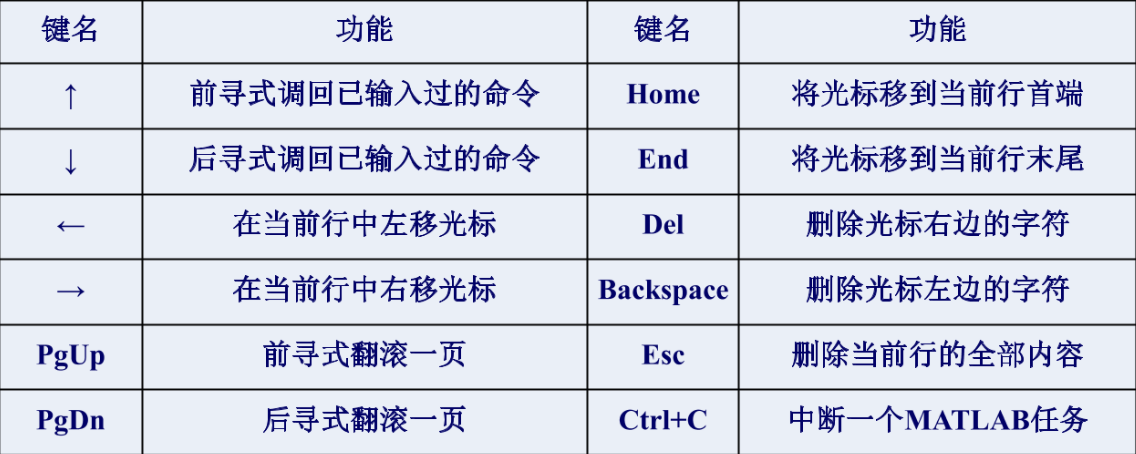
MATLAB——系统环境
MATLAB概述MATLAB的发展MATLAB:MATrix LABoratory1980年前后,Cleve Moler教授编写的Linpack 和Eispack的接口程序。1984年,MATLAB第1版(DOS版)1992年,MATLAB4.0版1994年,MATLAB 4.2版1997年,MATLAB 5.0版1999年&#x…...

2 GateWay工作流程+GateWay搭建
GateWay工作流程GateWay搭建 核心流程图如下: 核心概念: 客户端向 Spring Cloud Gateway 发出请求。如果Gateway Handler Mapping确定请求与路由匹配,则将其发送到Gateway Web Handler 处理程序。此处理程序通过特定于请求的Fliter链运行请求…...

【微信小程序】富文本rich-text的图片预览效果的几种方法
前言 使用原生小程序开发,实现在富文本rich-text中的图片预览效果的几种方法对比。 1.正则wx.previewImage(有明显不足) 一个不需要用额外组件或插件的方法: 思路:使用正则把图片的url进行剖离出来,push…...

通信网络-Socket、Java中的网络支持、多线程服务器
前言 通信网络-Socket、Java中的网络支持、多线程服务器 场景:使用java网络创建一个聊天室 博客地址:芒果橙的个人博客 文章目录前言通信网络-SocketTCP/IPTCP/IP 模型端口Java中的网络支持概念1. InetAddress2. URL3. Socket4. Datagram多线程服务器应用…...

搞懂 JS this、call、apply、bind
搞懂 JS this、call、apply、bind javascript 的 this ECMAScript 规范中这样写: this 关键字执行为当前执行环境的 ThisBinding。 MDN 上这样写: In most cases, the value of this is determined by how a function is called. 在绝大多数情况下&…...

力扣209长度最小的子数组
209. 长度最小的子数组 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 示例 1…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
